Łukasz Rafałowski BUDOWNICTWO ROK I GRUPA 4
Ćwiczenie 7
Badanie drgań wahadła sprężynowego
Wprowadzenie
-ruch drgający harmoniczny:
Ruch drgający - rodzaj ruchu w którym ciało porusza się tam i z powrotem po tej samej drodze
Ruch harmoniczny prosty: występuje gdy siła działająca na ciało drgające jest proporcjonalna do wychylenia ciała z pozycji równowagi i przeciwnie do niego skierowana.
Ruch harmoniczny prosty jest to taki ruch, w którym współrzędna opisująca ruch ciała zmienia się okresowo w sposób sinusoidalny. Wielkości występujące w poniższej funkcji charakteryzują ruch harmoniczny:
x=Acos(ωt+ φ)
φ-faza początkowa ruchu; jest to kąt, który określa wartość współrzędnej x w chwili t=0
A-amplituda drgań
ω - częstośc kołowa drgań spełniająca zależność
ω=2Πf=2Π/T
Okres drgań - czas, w którym wykonane jest jedno pełne drganie. W czasie okresu ciało przejdzie dwukrotnie każdy punkt swojej drogi i wraca do stanu początkowego.
Częstotliwość drgań - jest to liczba drgań przypadających na jednostkę czasu.
Okres i częstotliwość związane są zależnością:
f*T=1
Zależność pomiędzy współrzędną położenia ciała, jego przyspieszeniem i częstościa kołową drgań w ruchu harmonicznym:
a=- ω2x.
Ruch drgający ciała zawieszonego na sprężynie:
Celem naszego doświadczenia jest obserwacja ruchu harmonicznego ciężarka zawieszonego na sprężynie, tzw. wahadła sprężynowego. Ciężarek zawieszony na sprężynie spoczywa w położeniu, Które jest położeniem równowagi. Jeśli ciężarek pociągniemy w dół poniżej położenia równowagi i puścimy, zacznie on wykonywać drgania w dół i w górę. Zgodnie z prawem Hooka, przy małych odkształceniach, siła sprężystości jest proporcjonalna do odkształcenia x0:
F0=-kx0
Stała k jest tutaj współczynnikiem sprężystości sprężyny.
![]()
Współrzędną spoczynkowego odkształcenia x0 otrzymamy z warunku równowagi sił: P+F0=0.; wartości tych wektorów muszą być więc jednakowe: mg=kx0. Jeśli zmierzymy x0 dla znanej masy m zawieszonej na sprężynie, możemy wyznaczyć jej współczynnik sprężystości k:
Jeszcze wzór na okres drgań:
![]()
Jak widać okres drgań nie zależy od amplitudy A - jest to prawo izochronizmu wahadła sprężynowego.
Z energetycznych rozważań o ruchu drgającym można wyprowadzić wzór uwzględniający fakt, że sprężyna ma swoją masę. Ma on postać:
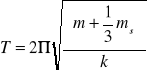
Wykonanie doświadczenia
Wyznaczanie współczynnika sprężystości sprężyny:
Zawieszamy sprężynę na statywie i do jej końca przymocowujemy lekki plastykowy wskaźnik. Na podziałce liniowej połączonej ze statywem odczytujemy położenie poziomej kreski zaznaczonej na wskaźniku.
Do wskaźnika doczepiamy odważnik o znanej masie i ponownie odczytujemy położenie kreski wskaźnika. Obliczamy wydłużenie sprężyny.
Obliczamy ciężar zawieszonej masy i współczynnik sprężystości k.
Pomiary wykonujemy dla trzech różnych ciężarków i obliczamy średnią wartość k.
Sprawdzanie prawa izochronizmu wahadła :
Obciążmy sprężynę odważnikiem, odciągamy go w dół o pewną wielkość i mierzymy czas n pełnych drgań wahadła. Dla tej samej amplitudy drgań powtarzamy te pomiary trzykrotnie. Obliczamy średni czas n drgań, a następnie okres ruchu drgającego.
Pomiary okresu powtarzamy jeszcze przy dwóch innych, odpowiednio powiększonych amplitudach drgań.
Wyznaczanie masy ciężarka :
Masa m. jest sumą masy badanej mx i masy wskaźnika m.w. Masę m.x obliczamy więc ze wzoru:
![]()
Obliczenia:
Wyznaczanie masy ciężarka:
![]()
![]()
Rachunek błędów
Δk=maxk-ki, i=1,2,3
Δk=0%
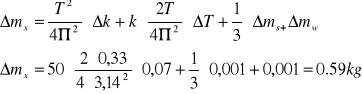
Δmx=5,98%
Wnioski
Potwierdziło się prawo izchronizmu wahadła - rzeczywiście okres drgań nie zależy od amplitudy.
Szukane wielkości; współczynnika sprężystości sprężyny k=50, natomiast obliczona masa ciężarka m=0,124kg.
Nasze obliczenia są z pewnym błędem, co wynika głównie z niedokładności pomiarów, niedoskonałości osób wykonujących doświadczenie i z małej dokładności urządzeń mierzących.
![]()
![]()
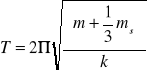
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Ćwiczenie55, Ćwiczenie 55 (1), Łukasz Rafałowski BUDOWNCTWO rok I
Ćwiczenie 47, Ćwiczenie 47 (3), Łukasz Rafałowski BUDOWNICTWO ROK I GRUPA 4
Ćwiczenie C2, Ćwiczenie C2 (3), Łukasz Rafałowski
Ćwiczenie C2, Ćwiczenie C2, Łukasz Rafałowski
Temat i zagadnienia na pierwsze ćwiczenia z dydaktyki - me tody, Studia, ROK I, dydaktyka
Ćwiczenie nr 35, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
ćwiczenia ( II półrocze ), College, Pedagogika, rok II, Pedagogika opiekuńcza
Ćwiczenie nr 44, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
pedagogika ćwiczenia sciaga rok1, studia pedagogiczne, Rok 4, Współczesne kierunki w pedagogice - Pr
Ćwiczenie nr 50a, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwic
Ćwiczenia 2, Studia, Pedagogika specjalna, Licencjat, I rok, Psychologia społeczna, Ćwiczenia
Ćwiczenia 8, Studia, Pedagogika specjalna, Licencjat, I rok, Biomedyczne podstawy rozwoju, Ćwiczenia
Rynek ćwiczenia ściąga, zootechnika UPH Siedlce, 4 rok 1 semest
lekarski-cwiczenie-1-15, Zakład Biologii Ogólnej
lekarski-cwiczenie-1-15, Zakład Biologii Ogólnej
Ćwiczenie nr 33a, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwi
więcej podobnych podstron