POLITECHNIKA WARSZAWSKA WYDZIAŁ TRANSPORTU

Laboratorium z przedmiotu: PODSTAWY TECHNIKI POMIAROWEJ Ćwiczenie nr 3. Temat : Ocena wyników ekstremalnych i testowanie hipotezy zgodności dla wyników eksperymentalnych. Grupa LTK sem VI Zespół nr 1 : 1. Halina Kobylińska 2. Lech Kielech 3. Grzegorz Krawczyk 4. Lech Olszewski Data wykonania ćwiczenia : 13.05.2001r.

1. WSTĘP TEORETYCZNY

Wszystkie badane wielkości zmienne, charakteryzujące zjawiska fizyczne, można podzielić na sygnały zdeterminowane i niezdeterminowane. Do sygnałów zdeterminowanych zalicza się takie, które można opisać za pomocą ścisłych zależności matematycznych lub z dużym przybliżeniem mogą być opisane ścisłymi zależnościami matematycznymi. Przykładem może być tor ruchu satelity po orbicie okołoziemskiej. Istnieje jednak wiele innych zjawisk fizycznych, które mają charakter niezdeterminowany. Są to sygnały których nie można opisać za pomocą ścisłych zależności matematycznych. Nie można przewidzieć dokładnej wartości takiego sygnału w pewnej chwili w przyszłości. Są to z natury swojej sygnały losowe i nie mogą być one opisane ścisłymi równaniami, lecz za pomocą uśrednionych charakterystyk statystycznych. Wynik każdej konkretnej obserwacji jest tylko jednym z wielu możliwych wyników, jakie mogą się zdarzyć. Pojedyncza funkcja czasu opisująca zjawisko losowe nazywa się funkcją losową lub realizacją. Zbiór wszystkich funkcji losowych nazywa się procesem losowym lub procesem stochastycznym. Sygnał uzyskany w wyniku obserwacji losowego zjawiska fizycznego można zatem uważać za odcinek jednej fizycznej realizacji procesu losowego.

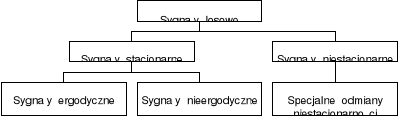
Rys. 1 Klasyfikacja sygnałów losowych

Sygnały losowe (stochastyczne) mogą być zbiorem nieprzeliczalnym lub przeliczalnym i będziemy mieli do czynienia z sygnałem ciągłym lub dyskretnym. Sygnał ciągły można zawsze zamienić na dyskretny, natomiast odwrotny proces posiada szereg ograniczeń.

Powiemy, że proces stochastyczny x(t) jest stacjonarny w węższym sensie, jeżeli dla dowolnego n, dowolnego układu wartości t₁, ....., t_n parametru t
T i dowolnego h takiego, że (t_i + h)
T (i = 1, ....., n) jest spełniona nierówność:

gdzie
- dystrybuanta rozkładu wielowymiarowego

F_t(x) = F_t-t(x) = F₀(x)

Oznacza to, że rozkład jednomiarowy procesu stacjonarnego w węższym sensie jest jednakowy dla każdej chwili, natomiast rozkład dwuwymiarowy zależy tylko od różnicy chwil, dla których przyjęto wartości procesu.

Proces stochastyczny X(t), dla którego istnieje wartość przeciętna E_x(t) i funkcja korelacyjna K_x(t₁, t₂) jest stacjonarny w szerszym sensie, jeżeli :

E_x(t) = const.,

K_x(t₁, t₂) = K_x(t₁ - t₂) = K_x(τ); τ = t₁ - t₂

tzn. Wartości funkcji autokoleracji zależą tylko od różnicy τ = t₁ - t₂.

Czas trwania pomiaru zazwyczaj oznaczamy jako T i wyznaczenie jego wartości jest związane z analizą w dziedzinie częstotliwości. Jeśli ustalimy charakter badanego zjawiska, którego parametry i funkcje mierzymy, to ważnym zadaniem jest określenie zakresu pomiaru w trzech dziedzinach. Zakres pomiaru w dziedzinie częstotliwości ustalimy wyznaczając dolny zakres częstotliwości (będziemy posługiwać się częstotliwością f) oraz górny zakres częstotliwości. Na jakie wielkości w innych dziedzinach ma zakres częstotliwości wpływ? Dolna częstotliwość wpływa na czas pomiaru T.

Jeśli f maleje do 0, to T rośnie do ∞. Przy częstotliwości 0 mamy pomiar statyczny, dla f różnego od 0 - pomiar dynamiczny. Można przyjąć, że czas trwania pomiaru musi być większy lub równy okresowi najmniejszej częstotliwości.

Górny zakres częstotliwości ma wpływ na częstotliwość próbkowaną w procesie zamiany sygnału ciągłego w dyskretny. Częstotliwość próbkowania najczęściej nazywa się ∆t, aby można było mówić o górnym zakresie częstotliwości w analizie sygnału dyskretnego, to ∆t musi spełniać warunek Nyugvista, tj. ∆t musi być tak małe, aby można było zrobić co najmniej dwa odczyty w okresie najwyższej częstotliwości .

Te dwa elementy są niezwykle ważne w praktycznej analizie sygnałów będących realizacją procesu stochastycznego. Trzeba pamiętać, że wszelkie obliczenia analizy są wykonywane z wykorzystaniem komputera, czyli są to zbiory przeliczalne ograniczone.

Rozważmy teraz realizację procesu stochastycznego i wyznaczamy częstości występowania amplitudy o określonej wartości.

Rys. 2. Przykładowy przebieg procesu losowego

2. CEL ĆWICZENIA

Celem ćwiczenia było zapoznanie się z podstawowymi metodami oceny wyników pomiarów, ze zwróceniem uwagi na wartości ekstremalne oraz dobór odpowiedniej charakterystyki statystycznej.

3. WYKONANIE ĆWICZENIA

Podczas ćwiczenia naszym zadaniem było zweryfikowanie hipotezy o zgodności rozkładu przy użyciu programu numerycznego LSP4.

Program jest napisany w języku Fortran w trybie konwersacyjnym i realizuje następujące zadania :

• wczytuje dane ze zbioru na dysku ,

• podaje po analizie realizację procesu stochastycznego stacjonarnego i ergodycznego, oceniając wartości ekstremalne za pomocą testu Romanowskiego

• po odrzuceniu wyników ekstremalnych dzieli dane na klasy i oblicza częstości zdarzeń i dystrybuanty empiryczne w każdej klasie dla tego rozkładu

• korzysta z metody funkcji największej wiarygodności i oblicza parametry danego rozkładu

• dla każdego typu rozkładu teoretycznego : gamma, Rayleigha, normalnego i logarytmiczno-normalnego ( w każdej klasie ) dokonuje weryfikacji hipotezy o zgodności rozkładu empirycznego z każdym z rozkładów teoretycznych dla wybranego poziomu istotności

4. WYKRESY

Otrzymaliśmy wydruki wykresów ( w załaczeniu) dla sygnałów losowych tj. dla sygnału S1 i dla sygnału S2.

5. WNIOSKI

Analizując otrzymane wykresy sygnałów S1 i S2 wynika, że sygnały są sygnałami ergodycznymi gdyż wartość średnia i funkcja korelacji( jak również inne momenty uzyskane przy wyznaczaniu w czasie) równają się odpowiednim średnim w zbiorze.

Należy zauważyć, że tylko procesy stacjonarne mogą wykazywać cechę ergodyczności. Procesy stochastyczne odpowiadające stacjonarnym zjawiskom fizycznym są na ogół ergodyczne i można prawidłowo wyznaczyć charakterystyki stacjonarnego procesu losowego na podstawie jednej realizacji, która posiada dostatecznie długi czas trwania - pomiaru.

5

f maleje

T rośnie

0

f

---