Jelenia Góra, 22.05.2000r.

Teoria obwodów 2

-laboratorium

Temat ćwiczenia:

SZEREGI FOURIERA

data wykonania ćwiczenia: 15.05.2000r.

grupa laboratoryjna: PONIEDZIAŁEK GODZ. 12.00

wykonali: Anna Miedzianowska

Sławomir Kukiełka

CZĘŚĆ TEORETYCZNA

Z analizy matematycznej wynika, że każdą okresową funkcję czasu o okresie T, która w dowolnym przedziale długości T jest funkcją regularną o ograniczonej zmienności można rozłożyć w trygonometryczny szereg Fouriera o postaci:

Dzięki takiemu rozwinięciu możemy określić matematycznie widmo częstotliwościowe przebiegu jeszcze przed skonstruowaniem układu.

Rozwinięcie w szereg pozwala nam określić parametry przebiegu.

PRZEBIEG PROSTOKĄTNY

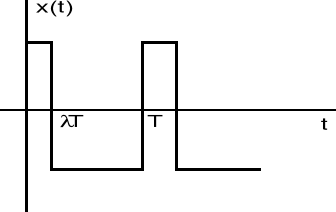
♦Obliczenia teoretyczne

Składowa stała:

Pierwsza harmoniczna :

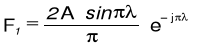
k-ta harmoniczna :

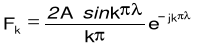
Poniższa tabela przedstawia porównanie wyników teoretycznych i praktycznych dla współczynnika λ = 0,5:

nr harmonicznej	FK [kHz]	Praktyczne A [mV]	Teoretyczne A [mV]
1	0,5	100	92
3	1,52	32	29,44
5	2,53	19	17,48
7	3,7	13,5	12,42
9	4,65	10,5	9,66
11	5,5	8	7,36

Dla współczynnika λ = 0,192:

nr harmonicznej			FK [kHz]	Praktyczne A [mV]		Teoretyczne A [mV]
1		0,503	50			46
3		1,5	32			29,4
5		2,5	16			14,72
7		3,72	8			7,36
9		4,65	9			8,28
11		5,5	5			4,6

PRZEBIEG PIŁOKSZTAŁTNY

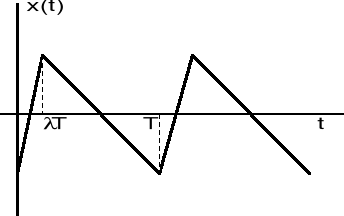
♦Obliczenia teoretyczne

Składowa stała:

Pierwsza harmoniczna :

k-ta harmoniczna :

Poniższa tabela przedstawia porównanie wyników teoretycznych i praktycznych dla współczynnika λ = 0,5:

nr harmonicznej			FK [kHz]	Praktyczne A [mV]		Teoretyczne A [mV]
1		0,5	72			66,24
3		1,52	8			7,36
5		2,55	2,4			2,21
7		3,7	1,1			1,01
9		4,65	0,9			0,83
11		5,52	0,2			0,18

Dla współczynnika λ = 0,192:

nr harmonicznej			FK [kHz]	Praktyczne A [mV]		Teoretyczne A [mV]
1		0,5	68			62,56
2		1,03	22			20,24
3		1,52	14,5			13,34
4		2	6			5,52
5		2,5	2			1,84
6		3	3			2,76

PRZEBIEG SINUSOIDALNY DWUPOŁÓWKOWY

♦Obliczenia teoretyczne

Składowa stała:

Pierwsza harmoniczna :

k-ta harmoniczna:

Poniższa tabela przedstawia porównanie wyników teoretycznych i praktycznych dla współczynnika λ = 0,5:

nr harmonicznej	FK [kHz]	Praktyczne A [mV]	Teoretyczne A [mV]
1	1,04	38	34,96
2	2,01	7,1	6,53
3	3,15	2,9	2,67
4	4,2	1,5	1,38
5	5,07	0,85	0,78
6	6	0,16	0,15
7	7	0,52	0,48
8	8	0,08	0,07
9	9,2	0,25	0,23
10	10,3	0,05	0,05
11	11	0,065	0,06

PRZEBIEG SINUSOIDALNY JEDNOPOŁÓWKOWY

♦Obliczenia teoretyczne

Składowa stała :

Pierwsza harmoniczna :

k-ta harmoniczna :

Poniższa tabela przedstawia porównanie wyników teoretycznych i praktycznych dla współczynnika λ = 0,5:

nr harmonicznej	FK [kHz]	Praktyczne A [mV]	Teoretyczne A [mV]
1	0,5	42	4,24
2	1,04	18	19,08
4	2	3,6	3,82
6	3	3	3,18
8	4,2	0,8	0,85
10	4,8	0,55	0,58

WNIOSKI

W ćwiczeniu zajęliśmy się badaniem widma różnych sygnałów okresowych. Były to:

- przebieg prostokątny,

- przebieg piłokształtny,

- przebieg sinusoidalny jednopołówkowy,

- przebieg sinusoidalny dwupołówkowy.

Pomiarów dokonywaliśmy dla λ = 0,5, a dla przebiegów niesinusoidalnych również dla λ = 0,19. Wyniki pomiarów są porównywalne z teoretycznymi i niewiele się różnią. Różnice te mogą wynikać z błędów miernika lub odczytu, czy występowania zakłóceń.

Na podstawie przeprowadzonych pomiarów doszliśmy do wniosku, że najszybciej wytłumianym sygnałem jest sygnał piłokształtny, natomiast najwolniej wytłumianym - prostokątny. Oznacza to, iż do wiernego odtworzenia przebiegu piłokształtnego wystarczy mniej składowych niż dla przebiegu prostokątnego.

Pomimo nieznacznych różnic między pomiarami, a teoretycznymi wartościami możemy wiarygodnie określić jakie będzie widmo częstotliwościowe danego przebiegu.

---