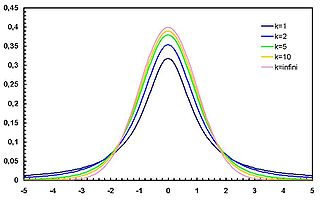
Rozkład Studenta - (rozkład t lub rozkład t-Studenta) ciągły rozkład prawdopodobieństwa stosowany często w statystyce w procedurach testowania hipotez statystycznych i przy ocenie błędów pomiaru. Przy opracowaniu wyników pomiarów często powstaje zagadnienie oszacowania przedziału, w którym leży, z określonym prawdopodobieństwem, rzeczywista wartość mierzona, jeśli dysponujemy tylko wynikami n pomiarów, dla których możemy wyznaczyć takie parametry, jak średnia
i odchylenie standardowe
lub wariancja
(„z próby”), nie znamy natomiast odch. standardowego
w populacji. Zagadnienie to rozwiązał (w 1908r.) W.S.Gosset (pseudonim Student) podając funkcję zależną od wyników pomiarów Xi, a niezależną od
.
Estymator jest statystyką służącą do szacowania wartości parametru rozkładu.Celem zastosowania estymatora jest znalezienie parametru rozkładu cechy w populacji.Przykładowo badamy rozkład wzrostu ludności w Polsce. Zakładamy, że rozkład tej cechy X w populacji jest rozkładem normalnym, zaś szukaną wielkością jest wartość oczekiwana m. Wartość m jest zatem szukanym parametrem rozkładu cechy X. W celu oszacowania tych wielkości zbieramy dane z próby losowej o liczebności n. Następnym krokiem będzie znalezienie wygodnej statystyki
z próby, która posłuży do oszacowania parametru m. Rolę takiej statystyki może spełniać wartość średnia z próby. Mówimy zatem, że wartość średnia z próby jest estymatorem wartości oczekiwanej rozkładu normalnego. Obliczoną przez nas na podstawie konkretnej próby wartość średnią nazywamy oceną parametru.
będzie rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby
, indeksowaną parametrem
(w szczególności może to być wektor parametrów rzeczywistych).
opisuje wielowymiarowy łączny rozkład wszystkich obserwacji w próbie
.
Zagadnienie estymacji punktowej polega na takim skonstruowaniu pewnej statystyki
zwanej estymatorem, aby wartości
były bliskie (w jakimś ustalonym sensie) wartości
. W szczególności, jeśli estymowany jest tylko jeden z parametrów rozkładu (czyli jedna ze współrzędnych wektora
), to odległość między
i
liczona jest tylko dla tej współrzędnej.
Ponieważ każda ze zmiennych losowych
ma rozkład identyczny z rozkładem cechy
w populacji generalnej, a rozkład ten zależy od parametru
, estymatory są zmiennymi losowymi, mającymi rozkład również zależny od parametru
.
Estymacja przedziałowa w jednowymiarowym przypadku polega na skonstruowaniu dwóch statystyk
i
takich, że zachodzi:
gdzie
jest ustalonym prawdopodobieństwem (tzw. poziom ufności). Przedział
to przedział ufności na poziomie
.
O estymacji z zadaną precyzją mówi się jeśli nałożone jest górne ograniczenie na wielkość
.
Oczywiście ocena parametru będzie prawie zawsze różnić się od oryginalnej wartości parametru
. Wprowadza się zatem miarę błędu estymacji:
Błąd szacunku
Własności estymatorów
Definicja estymatora pozostawia dużą dowolność w wybraniu danej statystyki do szacowania parametru, nie pozwalając jednocześnie na ocenę która ze statystyk jest "dobrym" estymatorem. Aby sprawdzić, czy dana statystyka jest dobrym kandydatem na estymator parametru, powinniśmy sprawdzić, czy spełnia ona zestaw własności charakteryzujących estymator.
Nieobciążoność
Estymator jest nieobciążony, jeśli wartość oczekiwana rozkładu estymatora jest równa wartości szacowanego parametru:
Jeśli różnica pomiędzy wartością oczekiwaną rozkładu estymatora a wartością szacowanego parametru jest zależna funkcyjnie od estymatora:
to estymator nazywamy obciążonym, zaś samą różnicę nazywamy obciążeniem estymatora.
Asymptotyczna nieobciążoność
Estymator nazywamy asymptotycznie nieobciążonym, jeśli obciążenie estymatora dąży do zera przy rosnącej liczebności próby:
Każdy estymator nieobciążony jest oczywiście estymatorem asymptotycznie nieobciążonym.
Zgodność
Oznacza to, że jeśli rośnie liczebność próby, rośnie też prawdopodobieństwo, że oszacowanie przy pomocy estymatora będzie przyjmować wartości coraz bliższe wartości szacowanego parametru. Inaczej: zwiększając liczebność próby, zmniejszamy ryzyko popełnienia błędu.
Wyszukiwarka
Podobne podstrony:
Rozklad Studenta, Studia, 1-stopień, inżynierka, Ochrona Środowiska, Statystyka
Rozklad Studenta, Studia, 1-stopień, inżynierka, Ochrona Środowiska, Statystyka
5 PPOO Empiryczny rozkład prawdopodobieństwa(1)
rozkład zmiennych losowych itp., statystyka matematyczna(1)
0 Podstawowe rozklady prawdopdobienstwaid 1848
ROZKŁADY PRAWDOP(1)
Zmienna losowa i rozklad prawdopodobienstwa - zadania, Pliki, Studia PK (Mechaniczny & WIL)
Niezawodnosc Rozklady prawdopodobienstwa, id
Kamys B Tablice podstawowych rozkładów prawdopodobieństwa (kwantyle)
5 rozklady prawdopodobienstwa i Nieznany (2)
Estymacja parametr w rozkladu prawdopodobienstwa, Estymacja parametrów rozkładu prawdopodobieństwa:
35H8? ralf majorkiewicz przykladowy rozkład prawdopodobieństw
cw Rozklady prawdopod
rozkład - chi kwadrat itd, statystyka matematyczna(1)
podstawowe rozklady prawdopodob Nieznany
więcej podobnych podstron