NIEZAWODNOŚĆ
* Rozkłady prawdopodobieństwa,
* Przykładowe zadania.

2012



Rozkład zmiennej losowej

– opis wartości

przyjmowanych przez zmienną losową przy pomocy
prawdopodobieństw (lub gęstości prawdopodobieństw) z
jakimi one występują.

Dla :



obiektu nienaprawialnego

– zmienną losową jest ilość wykonanej

pracy do momentu uszkodzenia,



obiektu naprawialnego

– zmienną losową jest ilość pracy

wykonanej między kolejnymi uszkodzeniami,



grupy obiektów nienaprawialnych

– zmienną losową jest ilość

obiektów, które uległy uszkodzeniu podczas zadanego okresu
czasu,



grupy obiektów naprawialnych

– zmienną losową jest ilość

uszkodzeń w grupie, podczas zadanego okresu czasu.

RODZAJE ZMIENNYCH LOSOWYCH



Dyskretne

– liczba uszkodzonych obiektów, liczba uszkodzeń,



Ciągłe

– ilość wykonanej pracy do momentu uszkodzenia, ilość

wykonanej pracy między uszkodzeniami, czas naprawy urządzenia
naprawialnego.

RODZAJE ROZKŁADÓW PRAWDOPODOBIEŃSTWA

NAJCZĘŚCIEJ WYSTĘPUJĄCYMI ROZKŁADAMI

W ZAGADNIENIACH NIEZAWODNOŚCI SĄ:



ROZKŁADY CIĄGŁE

-

normalny,

-

wykładniczy,

-

Weibulla,

-

gamma,

-

logarytmo-normalny.



ROZKŁADY DYSKRETNE

-

dwumianowy,

-

Poissona.

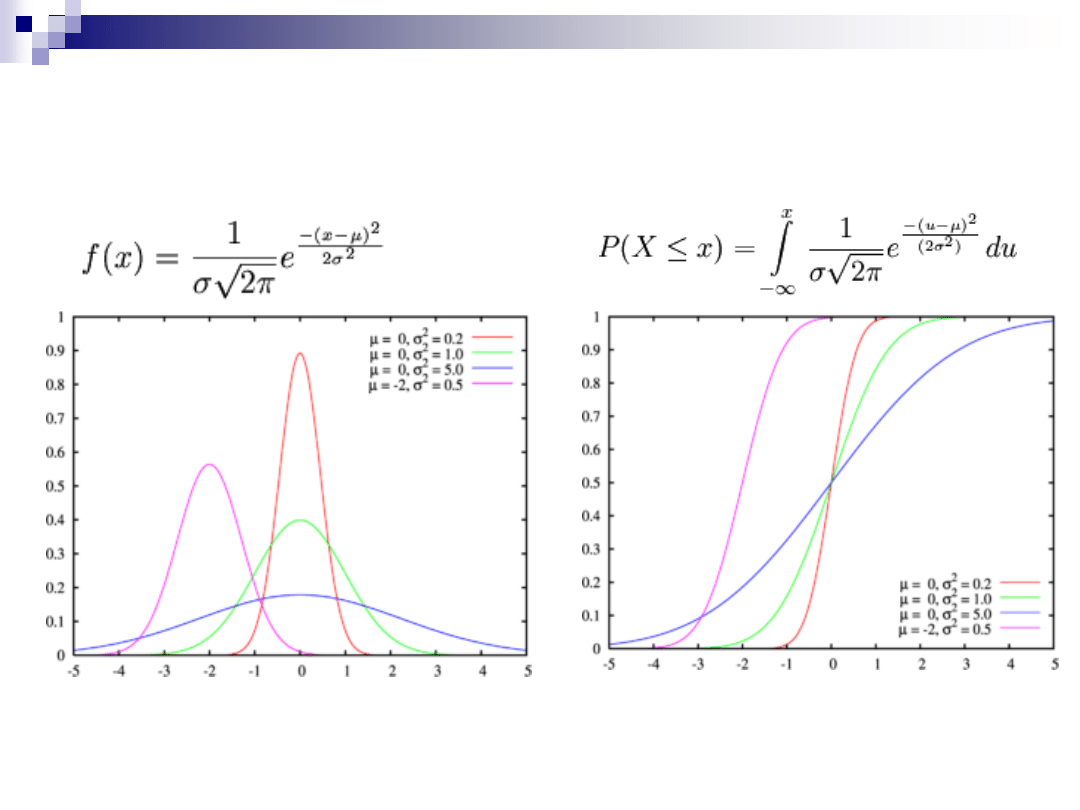
ROZKŁADY CIĄGŁE –

NORMALNY ( GAUSSA)

Funkcja gęstości

Dystrybuanta

ROZKŁADY CIĄGŁE –

NORMALNY ( GAUSSA) -

ZASTOSOWANIE

•

CZAS NAPRAWY obiektów NAPRAWIALNYCH w WIELU
przypadkach ma w przybliżeniu rozkład normalny,

•

ILOŚĆ WYKONANEJ PRACY dla obiektów
NIENAPRAWIALNYCH ma NIEKIEDY W PRZYBLIŻENIU
rozkład normalny,

•

Rozkład normalny stosuje się CZĘSTO do OBLICZEŃ
PRZYBLIŻONYCH, gdy wartości zmiennej losowej mają rozkład
DWUMIANOWY lub POISSONA.

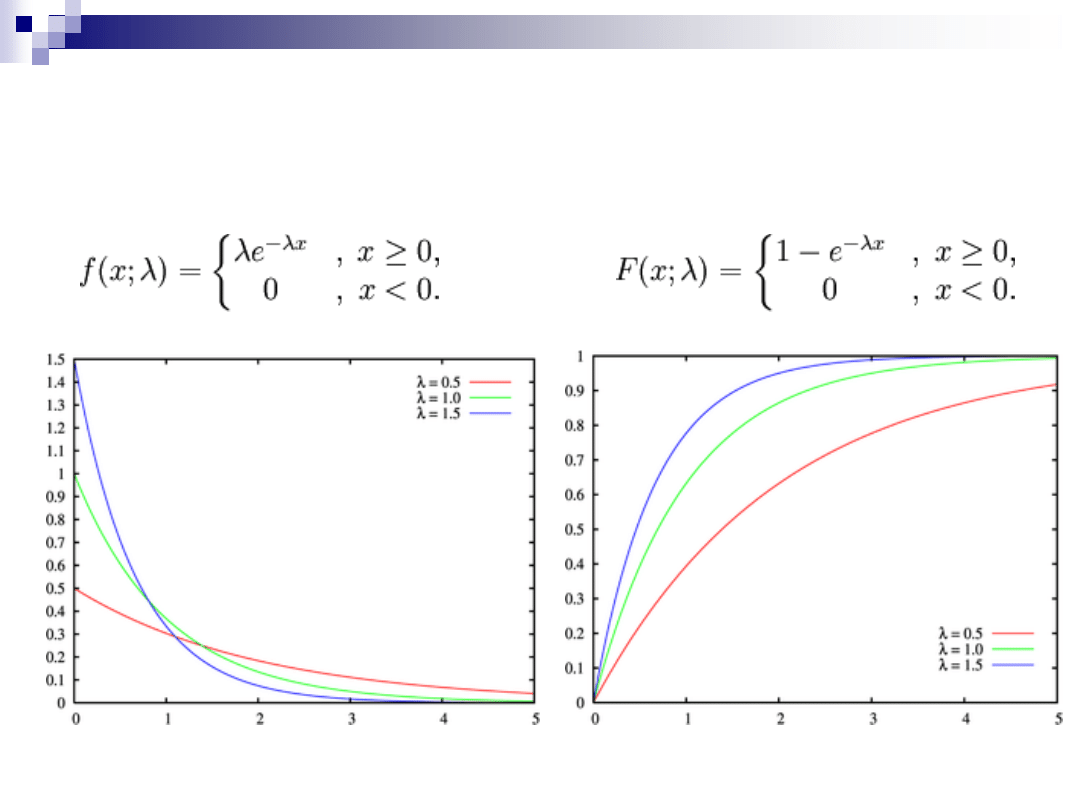
ROZKŁADY CIĄGŁE –

WYKŁADNICZY

Funkcja gęstości

Dystrybuanta

ROZKŁADY CIĄGŁE –

WYKŁADNICZY -

ZASTOSOWANIE

•

ILOŚĆ WYKONANEJ PRACY WIELU NIENAPRAWIALNYCH
elementów aparatury elektronicznej ma rozkład wykładniczy
(dotyczy to uszkodzeń nagłych, z niewielkim wpływem zużycia i
starzenia się badanych elementów),

•

Gdy strumień uszkodzeń NAPRAWIALNYCH elementów jest
jednorodnym strumieniem Poissona, to ILOŚĆ PRACY MIĘDZY
SĄSIEDNIMI USZKODZENIAMI ma rozkład WYKŁADNICZY,

•

Przyjmuje się też W PIERWSZYM PRZYBLIŻENIU,
że CZAS NAPRAWY ma rozkład wykładniczy.

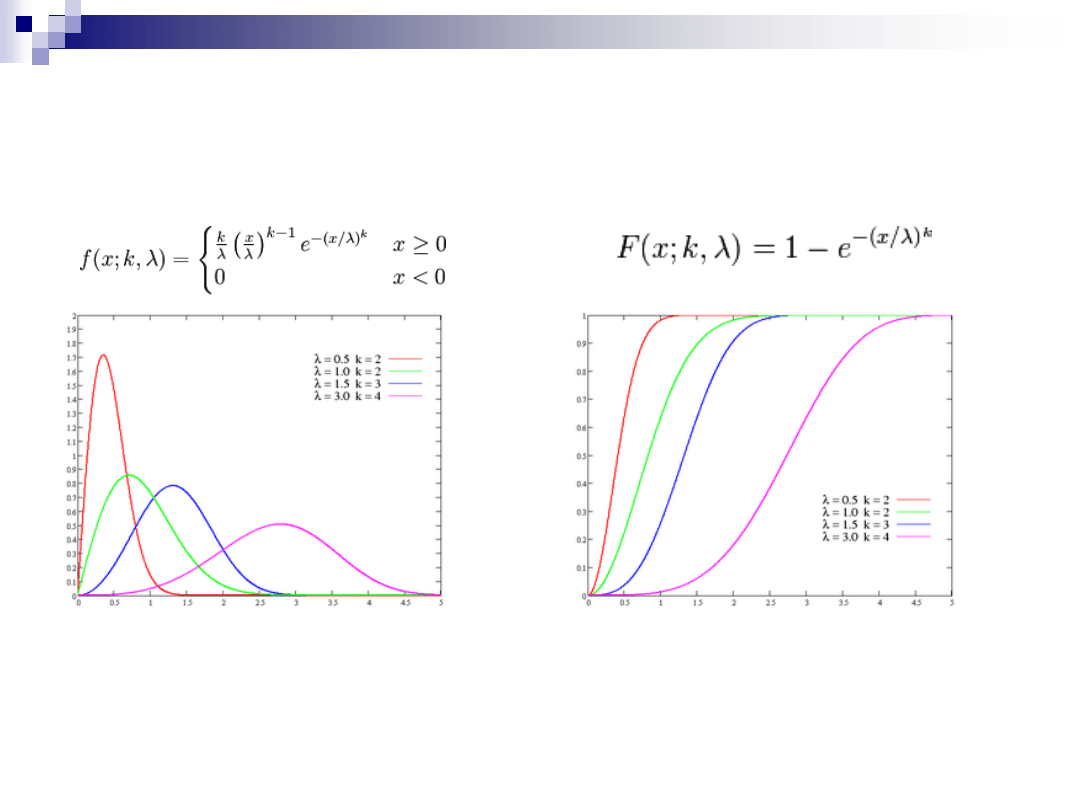
ROZKŁADY CIĄGŁE –

WEIBULLA

Funkcja gęstości

Dystrybuanta

Parametr k

rozkładu określa zachowanie prawdopodobieństwa awarii w czasie:



dla k

<1 prawdopodobieństwo awarii maleje z czasem. W przypadku modelowania awarii urządzenia sugeruje

to, że egzemplarze mogą posiadać wady fabryczne i powoli wypadają z populacji.



dla k

=1 (rozkład wykładniczy) prawdopodobieństwo jest stałe. Sugeruje to, że awarie mają charakter

zewnętrznych zdarzeń losowych.



dla k

>1 prawdopodobieństwo rośnie z czasem. Sugeruje to zużycie części z upływem czasu jako główną

przyczynę awaryjności.

ROZKŁADY CIĄGŁE –

WEIBULLA -

ZASTOSOWANIE

•

ILOŚĆ WYKONANEJ PRACY dla WIELU OBIEKTÓW
NIENAPRAWIALNYCH ma rozkład Weibulla, do takich obiektów
zalicza się przykładowo:

-

Łożyska toczne,

-

Lampy elektronowe,

-

Elementy półprzewodnikowe,

-

Przyrządy ultrawielkiej częstotliwości,

-

Obiekty, w których uszkodzenia są wynikiem zmęczenia
materiału.

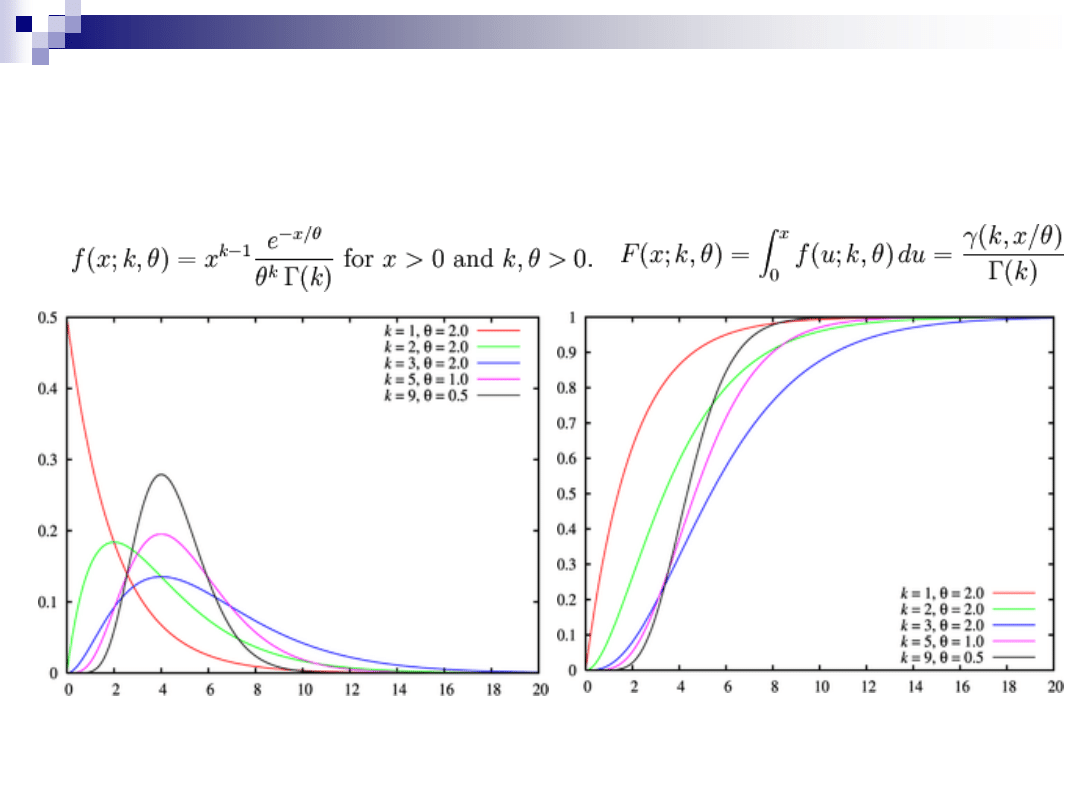
ROZKŁADY CIĄGŁE –

GAMMA

Funkcja gęstości

Dystrybuanta

ROZKŁADY CIĄGŁE –

GAMMA -

ZASTOSOWANIE

•

Gdy strumień uszkodzeń NAPRAWIALNYCH elementów jest
jednorodnym strumieniem Poissona, to ILOŚĆ PRACY MIĘDZY
NIESĄSIEDNIMI USZKODZENIAMI ma rozkład gamma,

•

W WIELU przypadkach CZAS NAPRAWY ma rozkład gamma.

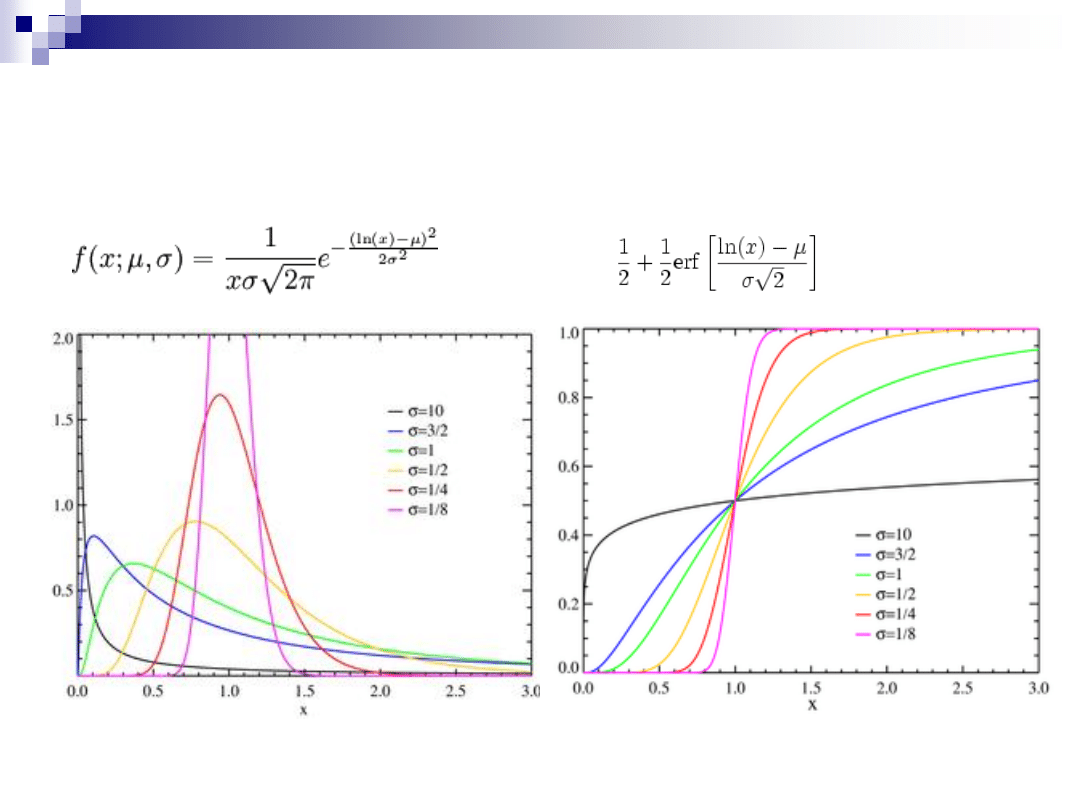
ROZKŁADY CIĄGŁE –

LOGARYTMO-NORMALNY

Funkcja gęstości

Dystrybuanta

ROZKŁADY CIĄGŁE –

LOGARYTMO-NORMALNY

-

ZASTOSOWANIE

•

ILOŚĆ WYKONANEJ PRACY dla WIELU OBIEKTÓW
NIENAPRAWIALNYCH ma rozkład logarytmo-normalny, do
takich obiektów zalicza się przykładowo:

-

Lampy elektronowe,

-

Obiekty, w których uszkodzenia są wynikiem zmęczenia
materiału.

•

W WIELU przypadkach CZAS NAPRAWY ma rozkład logarytmo-
normalny.

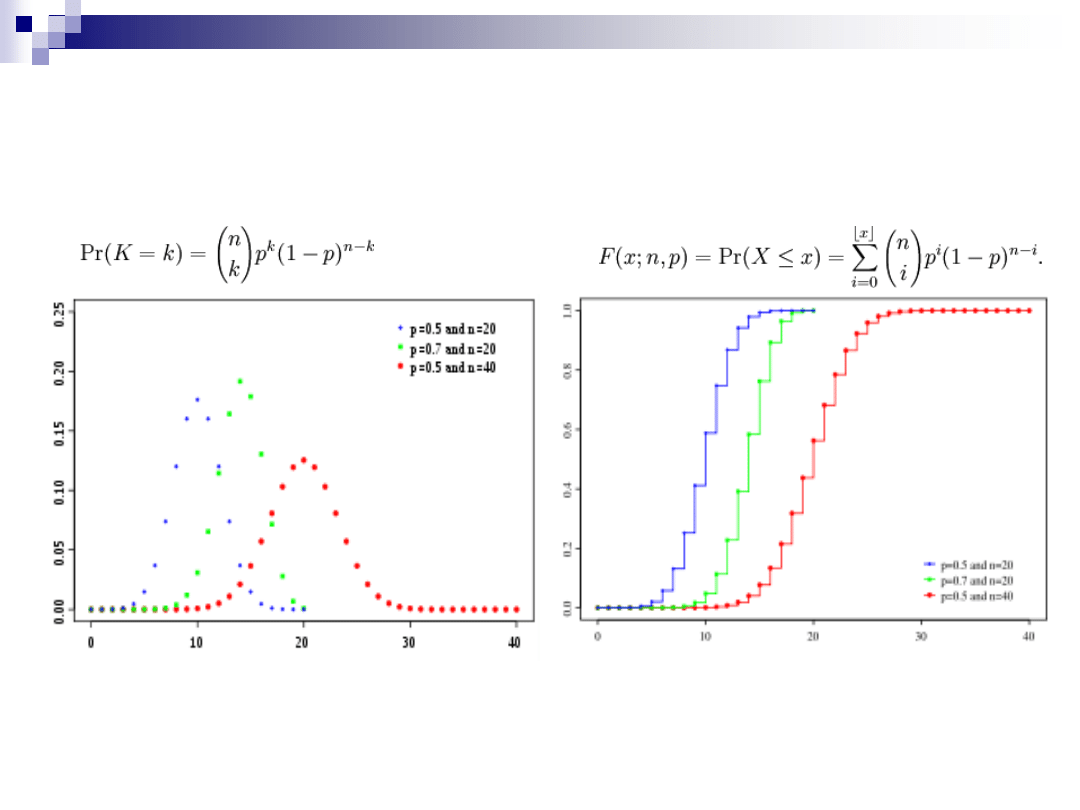
ROZKŁADY DYSKRETNE –

DWUMIANOWY

Funkcja gęstości

Dystrybuanta

ROZKŁADY DYSKRETNE –

DWUMIANOWY

-

ZASTOSOWANIE

•

W badanej GRUPIE obiektów NIENAPRAWIALNYCH dla
USTALONEJ ILOŚCI WYKONANEJ PRACY LICZBA
USZKODZONYCH OBIEKTÓW jest zmienną losową o rozkładzie
dwumianowym

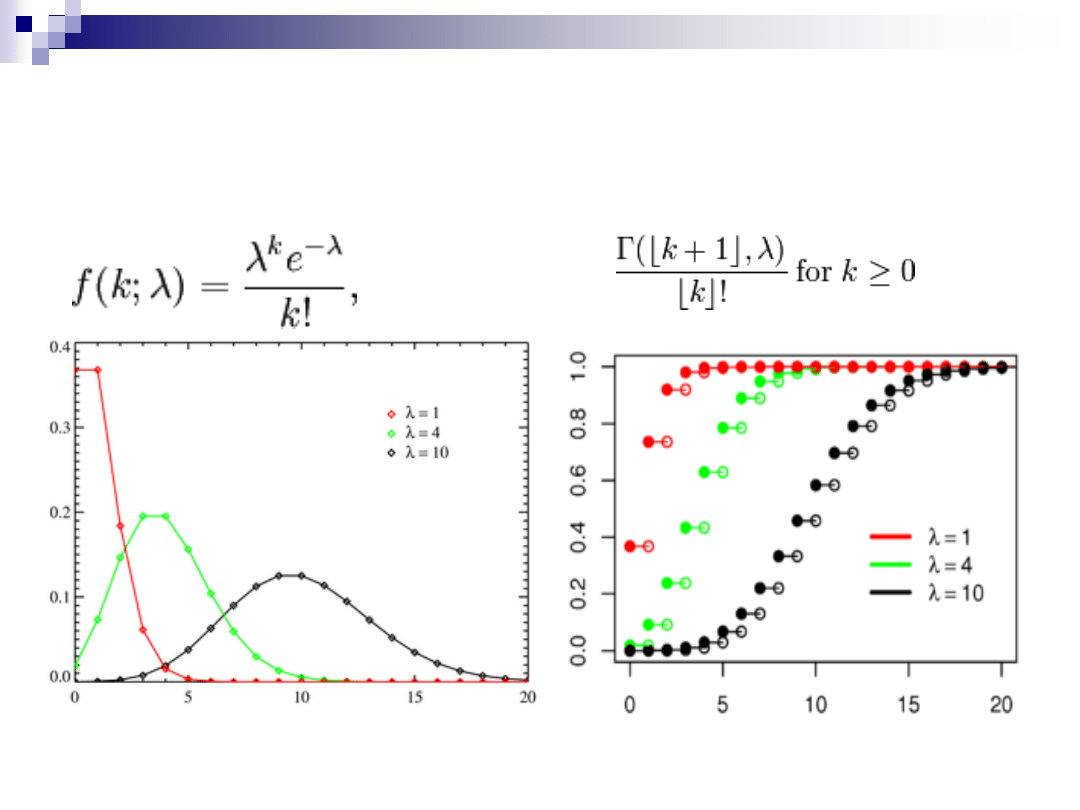
ROZKŁADY DYSKRETNE –

POISSONA

Funkcja gęstości

Dystrybuanta

ROZKŁADY DYSKRETNE –

POISSONA

-

ZASTOSOWANIE

•

Jeżeli dla obiektu naprawialnego strumień uszkodzeń jest
jednorodnym strumieniem Poissona, to LICZBA USZKODZEŃ
obiektu w czasie wykonywania określonej ilości pracy ma rozkład
Poissona,

•

W WIELU PRZYPADKACH przyjmuje się rozkład Poissona jako
DOBRE PRZYBLIŻENIE rozkładu dwumianowego.

PRZYKŁADOWE ZADANIA

•

ZADANIE 1:

Czas zdatności obiektu może być opisany rozkładem
wykładniczym. Jakie jest prawdopodobieństwo, że po upływie
czasu równego oczekiwanemu czasowi zdatności tego obiektu,
będzie on jeszcze zdatny do użytku?

Odp.: Prawdopodobieństwo, że po upływie oczekiwanego czasu

zdatności obiektu będzie on nadal sprawny wynosi 0,36.

PRZYKŁADOWE ZADANIA

•

ZADANIE 2:

Stwierdzono, że funkcja niezawodności pewnych urządzeń ma
postać :

Należy obliczyć gęstość prawdopodobieństwa uszkodzeń tych
urządzeń :