Politechnika Krakowska Fizyka Techniczna II Rok |
Michał Karczewski |
1999/2000 Semestr III |
Data :
|
Grupa : 1 Zespół : 2 |
|
Nr ćw.: 5 |
Podpis :
|
|
|
|
Ocena:
|
Badanie Drgań Tłumionych Wahadła Torsyjnego
![]()
Bryła sztywna obracalna około stałej osi obrotu i poddana momentowi sił M1, proporcjonalnemu do kąta odchylenia bryły z położenia równowagi φ, a skierowanemu przeciwnie do wychylenia
![]()
Wykonuje drgania proste, obrotowe o równaniu:
gdzie:
J - moment bezwładności bryły względem osi obrotu.
![]()
Rozwiązaniem tego równania jest:
gdzie:
Φ - amplituda kątowa drgań,
T - okres drgań
ε - faza początkowa.
Amplituda i okres są nie zmienne w czasie, przy czym okres nie zależy od amplitudy (izochronizm drgań). Jeżeli oprócz momentu M1 działają na ciało momenty sił skierowane przeciwnie do prędkości ciała, wówczas amplituda maleje z biegiem czasu; obserwujemy drgania zwane tłumionymi, zanikającymi lub gasnącymi
Prawo zanikania amplitudy zależy od rodzaju tłumienia. Rozpatrzmy dwa rodzaje tłumienia:
tłumienie momentem siły proporcjonalnym do prędkości ruchu φ i przeciwnie do niej skierowanym: M2 = k2 φ
tłumienie momentem stałym co do wartości, a przeciwnie skierowanym do φ;
Przypadek "a" występuje przy tłumieniu powolnych, mechanicznych drgań ciała zanurzonego w lepkiej cieczy lub przy tłumieniu drgań elektrycznych w obwodach elektrycznych. Przypadek "b" ma miejsce przy tłumieniu drgań mechanicznych tarciem kulombowskim. W przypadku "a" równanie ruchu ma postać:
Jego rozwiązaniem przy słabym tłumieniu ( k22 < 4Jk1 ) jest funkcja:
Stałe Ф i ε wyznaczamy z warunków początkowych. Niech np.: dla t=0, φ(0)= φ0 i φ(0)= φ0, wówczas:
Funkcja przedstawiona równaniem 2 nie jest funkcja periodyczną jak wynika z poniższego rysunku. Jej "okres ", tj czas, jaki upływa miedzy dwoma kolejnymi maksimami lub podwójny czas między dwoma kolejnymi przejściami przez 0 wynosi:
A więc jest dłuższy od okresu T drgań nie gasnących. Maksima funkcji [2] są przesunięte względem maksimów funkcji sinus kąta w lewo i wartości ich maleją z czasem. Ponieważ termin -amplituda- odnosi się do stałej wartości maksimów funkcji sinus, wyrażenie Фe-δt należało by nazwać amplitudę w cudzysłowie. "Amplituda" Фe-δt maleje z czasem według funkcji wykładniczej, logarytm "amplitudy" maleje liniowo z czasem
Obliczmy stosunek 2 kolejnych "amplitud" po tej samej stronie położenia równowagi
Stosunek ten jest stały i nosi nazwę stosunku tłumienia. Logarytm naturalny tego stosunku :
Nosi nazwę dekrementu logarytmicznego drgań tłumionych. Jest on również wartością charakterystyczną dla tych drgań.
W przypadku "b" równanie ma postać: Jφ = - kφ+M3
Rozwiązaniem tego równania a właściwie układu 2 równań różniczkowych jest drganie tłumione o amplitudzie malejącej według postępu arytmetycznego o wielkości Δφ=4M/k1 na 1 okres i nie zmienionym okresie :
Przyrząd składa się z kuli zawieszonej na stalowym drucie wlutowanym osiowo w walec, obracalny w łożysku za pośrednictwem pokrętła o niewielki kąt. Wiązka światła z rzutnika odbija się od zwierciadła przymocowanego do drutu i daje na skali plamkę świetlną. Podczas drgań obrotowych kuli plamka świetlna wykonuje drgania liniowe o odchyleniu x proporcjonalnym do kąta obrotu kuli φ, gdyż dla niewielkich kątów
(l jest odległością skali od zwierciadełka); stąd
Tłumienie proporcjonalne do prędkości ruchu realizujemy przez zanurzenie drgającej kuli w lepkiej cieczy, np. w wodzie; stąd nazwa tego rodzaju tłumienia: lepkościowe lub wiskotyczne. Tłumienie stałym momentem uzyskujemy, podstawiając pod kulę cienką blaszkę przesuwalną na statywie, której wysokość, a więc i nacisk na kulę można regulować za pomocą śruby.
Tłumienie pochodzące od lepkości powietrza i tarcia wewnętrznego w materiale drutu jest tak małe, że można je wobec obu rozpatrywanych momentów hamujących pominąć. Kulę wprawiamy w drganie przez powolny obrót zawieszenia z położenia zerowego w skrajne, a następnie szybki powrót do zera.
Pomiar okresu drgań wahadła torsyjnego:
Lp.
|
10 T [s] |
1. |
89,75 |
2. |
89,97 |
3. |
89,44 |
4. |
89,64 |
5. |
89,59 |
6. |
89,71 |
7. |
89,72 |
8. |
89,94 |
9. |
89,47 |
10. |
89,68 |
Średnia wartość 10T=89,68 [s]
Średnie odchylenie kwadratowe dane wzorem:
S10T= ~0,05 [s]
Smax=3* S10T ~0,02 [s]
Zatem okres drgań własnych wahadła torsyjnego wynosi :
T=+(8,97 ± 0,02) s
2.Pomiar amplitudy wychylenia względem czasu dla wahadła nietłumionego
Lp. |
X [dz] |
Lp. |
X[dz] |
1. |
162 |
11. |
157 |
161 |
12. |
154 |
|
159 |
13. |
155 |
|
159 |
14. |
154 |
|
160 |
15. |
152 |
|
166 |
16. |
155 |
|
157 |
17. |
155 |
|
159 |
18. |
153 |
|
156 |
19. |
154 |
|
155 |
20. |
154 |
3.Pomiar wychylenia wahadła torsyjnego tłumionego tarciem kulombowskim:
Lp. |
X [dz] |
Lp. |
X[dz] |
1. |
198 |
18. |
88 |
2. |
191 |
19. |
82 |
3. |
180 |
20. |
76 |
4. |
173 |
21. |
72 |
5. |
166 |
22. |
65 |
6. |
158 |
23. |
59 |
7. |
152 |
24. |
53 |
8. |
145 |
25. |
46 |
9. |
139 |
26. |
41 |
10. |
133 |
27. |
35 |
11. |
129 |
28. |
29 |
12. |
123 |
29. |
24 |
13. |
116 |
30. |
19 |
14. |
111 |
31. |
14 |
15. |
105 |
32. |
9 |
16. |
100 |
33. |
5 |
17. |
95 |
34. |
0 |
4.Pomiae okresu drgań tłumionych wahadła torsyjnego tłumionego oporem
wiskotycznym:
Lp.
|
10 T [s] |
1. |
90,22 |
2. |
90,31 |
3. |
90,28 |
4. |
90,69 |
5. |
90,37 |
6. |
90,46 |
7. |
90,53 |
8. |
90,34 |
9. |
90,53 |
10. |
90,20 |
Średnia wartość 10T=90,39 [s]
Średnie odchylenie kwadratowe dane wzorem:
S10T= ~0,05 [s]
Smax=3* S10T ~0,02 [s]
Zatem okres drgań własnych wahadła torsyjnego wynosi :
T=+(9,01 ± 0,02) s
4.Pomiar amplitudy wychylenia względem czasu dla wahadła tłumionego oporem wiskotycznym:
Lp. |
X[dz] |
Ln(X) |
Lp. |
X[dz] |
Ln(X) |
1. |
197 |
5,28 |
16. |
60 |
4,09 |
2. |
180 |
5,19 |
17. |
55 |
4,01 |
3. |
168 |
5,12 |
18. |
51 |
3,93 |
4. |
155 |
5,04 |
19. |
47 |
3,85 |
5. |
145 |
4,92 |
20. |
44 |
3,78 |
6. |
132 |
4,88 |
21. |
40 |
3,69 |
7. |
124 |
4,82 |
22. |
36 |
3,58 |
8. |
115 |
4,74 |
23. |
32 |
3,47 |
9. |
107 |
4,67 |
24. |
30 |
3,40 |
10. |
19 |
4,60 |
25. |
27 |
3,30 |
11. |
92 |
4,52 |
26. |
24 |
3,18 |
12. |
84 |
4,43 |
27. |
22 |
3,09 |
13. |
77 |
4,34 |
28. |
20 |
3,00 |
14. |
71 |
4,26 |
29. |
18 |
2,89 |
15. |
67 |
4,20 |
30. |
15 |
2,71 |
6.Obliczenie momentu kierującego k1:
k1 =4∏ , J= mR2
m=750 g
R=2,85 cm
Więc moment bezwładności:
J= 0,75 [kg]*(0,0285)2=243,68*10-6 kg*m2
k1=4*(3,1416)2 * =119,56 *10-3 [Nm]
7. Obliczenia dla ruchu wahadła torsyjnego tłumionego oporem
wiskotycznym
δϕ=
ϕ- spadek ampitudy na jeden okres
x~2ϕl
δx=2δϕl
k1 =119,56 *10-3 [Nm], współczynnik k1 jest taki sam jak dla dla drgań nietłumionych
δx=166 mm
l=86,5 cm
M===2,87*10-3[Nm]
8.Obliczenia dla ruchu wahadła torsyjnego tłumionego oporem
wiskotycznym
Wyznaczanie dekrementu logarytmicznego drgań na podstawie wykresu
ln(x)=f(x)
D== ln()=ln(ϕn) -ln(ϕn+1)
D=0,0854
k1= =118,5*10-6 [Nm]
k2==4,62*10-6 [Nms]
φ
t
3T
2T
T
Δφ
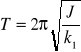
![]()
2T
6T
4T
8T
t
ln Φn
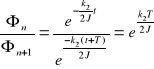
T
3T
2T
t
φ
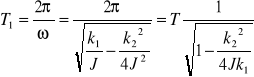
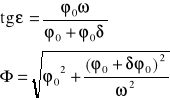
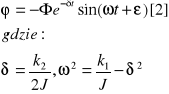
![]()
2T
T
3T
t
![]()
φ
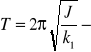
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
ćw.5, 05 Gorski, Politechnika Krakowska
ćw.5, 05 Bernady, Politechnika Krakowska
ćw.5, 05 Kuk 1, Politechnika Krakowska
ćw.19, 19 Karczewski, Politechnika Krakowska
ćw.19, 19 Karczewski, Politechnika Krakowska
ćw.17, 25 Karczewski, Politechnika Krakowska
ćw.40, 40 Karczewski, Politechnika Krakowska
ćw.21, 21, Politechnika Krakowska
ćw.34, opracowanie34, Politechnika Krakowska
ćw.27, 27, Politechnika Krakowska
ćw.5, 12 Balawender 2, Politechnika Krakowska
ćw.30, 42, Politechnika Krakowska
ćw.40, 40 Bernady, Politechnika Krakowska
ćw.19, 19 Bernady, Politechnika Krakowska
Konspekt do cw. lab.-termowizja, Energetyka Politechnika Krakowska Wydział Mechaniczny I stopień, Mi
ćw.39, 39 Gorski 2, Politechnika Krakowska
ćw.40, 40 Balawender, Politechnika Krakowska
Fizyka cw 1, Politechnika Krakowska BUDOWNICTWO, I ROK, Fizyka
ćw.33, 33 Bernady 2, Politechnika Krakowska
więcej podobnych podstron