I PRACOWNIA FIZYCZNA U. ŚL.
nr ćwiczenia:	temat :		Wyznaczanie napięcia powierzchniowego cieczy metodą rurek włoskowatych i metodą rozrywania warstwy powierzchniowej
22
imię i nazwisko :		ROBOT 23
rok studiów :		I		kierunek :	WYCHOWANIE TECHNICZNE
grupa :		10^30		data wykonania ćwiczenia :		7.05.19r.

Wstęp teoretyczny.

Siły Van der Waalsa (spójności).

Pomiędzy drobinami cieczy działają siły Van der Waalsa, zwane również siłami spójności. Ich wielkość zależy od odległości r pomiędzy drobinami:

gdzie:

C₁ i C₂ są stałymi, a wykładniki potęgowe n i m spełniają nierówność n<m, co w praktyce oznacza, że siły odpychające (drugi składnik równania) maleją wraz z odległością szybciej od sił przyciągających (składnik pierwszy). Dla bardzo małych odległości przeważają siły odpychające, a dla nieco większych - przyciągające. Obydwa rodzaje sił bardzo szybko maleją ze wzrostem odległości r.

Napięcie powierzchniowe.

Stosunek siły napięcia powierzchniowego do długości ograniczenia powierzchni cieczy nazywamy napięciem powierzchniowym:

Napięcie to ma podwójne znaczenie:

energetyczne - gdyż wyznacza energię potencjalną zmagazynowaną w 1m² błonki powierzchniowej:

siłowe - gdyż wyraża siłę przyłożoną do 1 m długości błonki:

Napięcie powierzchniowe zależy od:

• rodzaju cieczy: dla każdej cieczy jest ono inne, gdyż różne cząstki oddziaływują na siebie z różnymi siłami.

• temperatury: napięcie powierzchniowe maleje wraz ze wzrostem temperatury:

gdzie:

K - stała dla danej cieczy,

V - jej objętość molowa,

T_K - temperatura krytyczna.

Ciecze zwilżające i niezwilżające.

Działające między cieczą a ciałem stałym siły przylegania zależą od rodzaju ciał. Dla wody i szkła przewyższają one znacznie siły spójności. Z tego powodu woda pokrywa cienką warstwą powierzchnię ciała. Powierzchnia wody przy brzegu naczynia nie jest płaska. Siły powierzchniowe działają w kierunku jej zmniejszania, a przylegania - zwiększenia. W konsekwencji przy ściankach ciecz wznosi się w określony sposób. Jeżeli w cieczy zanurzymy rurkę szklaną lub rurkę włoskowatą, to w przypadku cieczy zwilżającej siły powierzchniowe spowodują wzniesienie jej menisku ponad poziom otaczającej cieczy lub obniżenie - w przypadku cieczy niezwilżającej (rtęć).

Siły powierzchniowe powodujące wzniesienie słupka cieczy działają na obwodzie kapilary (2r) i wynoszą:

.

Opracowanie wyników.

Do obliczeń błędów metodą statystyczną używam następujących zależności:

Wartość średnia

Odchylenie od średniej dla pojedynczego pomiaru:

Odchylenie standardowe dla próby:

Odchylenie standardowe pojedynczego pomiaru:

Błąd standardowy wartości średniej:

Metoda rurek włoskowatych.

1. Gęstość wody w temp 22⁰C
   

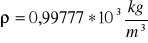
2. Wartość średnia h.

l.p.	h[mm]	i	i^2	s^2	s	σ	σm
1	74	-1	1	0,66667	0,8165	0,89443	0,36515
2	76	1	1
3	75	0	0
4	74	-1	1
5	76	1	1
6	75	0	0
hśr	75

3. Wartość średnia r.

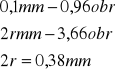
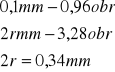
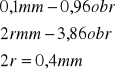
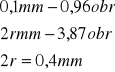
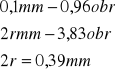
l.p.	2r	r[mm]	i	i^2	s^2	s	σ	σm
1	0,38	0,19	-0,001	0,00000	0,00012	0,01114	0,01245	0,00557
2	0,34	0,17	-0,021	0,00044
3	0,40	0,20	0,009	0,00008
4	0,40	0,20	0,009	0,00008
5	0,39	0,20	0,004	0,00002
rśr		0,191

4. Obliczam wartość σ i σ

ρ- gęstość badanej cieczy

g- przyspieszenie ziemskie

h- wysokość słupa cieczy

- kąt zetknięcia. Dla wody

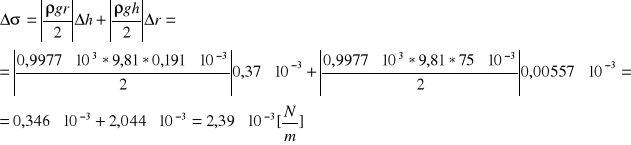
Metoda rozrywania warstwy powierzchniowej.

1. Wartość średnia l i l.

l.p.	l[mm]	i	i^2	s^2	s	σ	σm
1	43,35	-0,120	0,01440	0,00860	0,09274	0,10368	0,04637
2	43,60	0,130	0,01690
3	43,40	-0,070	0,00490
4	43,55	0,080	0,00640
5	43,45	-0,020	0,00040
lśr	43,470

2. Wartość średnia m₁ i m₁.

l.p.	m1[mg]	i	i^2	s^2	s	σ	σm
1	261	-6,4	40,96	182,53333	13,51049	14,8	6,04207
2	254	-13,4	179,56
3	252	-15,4	237,16
4	282	14,6	213,16
5	288	20,6	424,36
6	292	24,6	605,16
mśr	267,4

3. Wartość średnia m₂ i m₂.

l.p.	m2[mg]	i	i^2	s^2	s	σ	σm
1	423	-10	100	304	17,4356	19,09974	7,79744
2	450	17	289
3	408	-25	625
4	460	27	729
5	424	-9	81
6	398	-35	1225
mśr	433

4. Wartość średnia σ i σ.

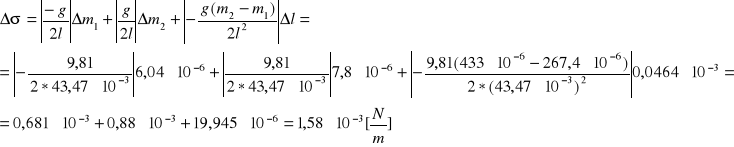
Wnioski.

Współczynniki obliczone dwoma różnymi metodami wynoszą odpowiednio:

dla metody rurek włoskowatych

;

dla metody rozrywania warstwy powierzchniowej

.

Współczynnik napięcia powierzchniowego dla wody w temperaturze 22⁰C wynosi
.

Jak widać współczynnik napięcia powierzchniowego obliczony metodą rurek włoskowatych jest zbliżony do odczytanego z tablic. Natomiast współczynnik napięcia powierzchniowego obliczony na podstawie rozrywania warstwy powierzchniowej znacznie odbiega od wartości tablicowej. Różnica ta może być spowodowana przez złe odczytanie masy m₁ lub m₂.

1

1