I PRACOWNIA FIZYCZNA U. ŚL.
nr ćwiczenia:	temat :		Wyznaczanie lepkości cieczy metodą Stokesa
20
imię i nazwisko :		Jordan
rok studiów :		I		kierunek :	WYCHOWANIE TECHNICZNE
grupa :		10^30		data wykonania ćwiczenia :		21.01.19r.

Wstęp teoretyczny.

Prawo Archimedesa

Ciało zanurzone w cieczy traci pozornie na wadze tyle ile waży wyparta przez nie ciecz.

Ciecz idealna - rzeczywista

Ciecze w danych warunkach posiadają wyraźnie określoną objętość, bardzo małą ściśliwość i wyraźnie ukształtowaną powierzchnię swobody. Przyjmujemy, że ciecz idealna jest nieściśliwa i nie posiada lepkości. Ciecz rzeczywista wykazuje dostrzegalną ściśliwość i lepkość.

Przepływ cieczy

Do opisu przepływu cieczy potrzebna jest znajomość prędkości przepływu w każdym jej punkcie i w każdej chwili. Prędkości te wyrażone są wzorami:

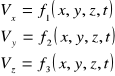
Składowe prędkości cząstek cieczy opisane są wzorami:

Równanie ciągłości cieczy wyrażające zasadę zachowania masy:

gdzie:

m - masa cieczy

S - przekrój poprzeczny

V - średnia prędkość przepływu

ρ - średnia gęstość przepływu

Przez każdy poprzeczny przekrój musi na jednostkę czasu przepłynąć taka sama masa cieczy. Dla cieczy idealnej:

Lepkość - wielkość zależna od temperatury, ciśnienia i rodzaju płynu, stanowiąca miarę tarcia wewnętrznego. Zgodnie z prawem Newtona:

gdzie:

F - siła styczna potrzebna do pokonania tarcia wewnętrznego

A- powierzchnia warstewek, odległych od siebie o dy, poruszających się prędkościami różniącymi się o dv

τ - naprężenie styczne proporcjonalne do gradientu prędkości względem odległości dv/dy

η - współczynnik proporcjonalności zwany lepkością dynamiczną

Jednostkami miary lepkości dynamicznej jest paskalosekunda.

Współczynnik lepkości obliczamy ze wzoru:

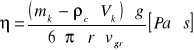
gdzie:

m_k - masa kulki

ρ_c - gęstość cieczy

V_k - objętość kulki

r - promień kulki

g - przyspieszenie ziemskie

v_gr - prędkość graniczna kulki w cieczy o nieograniczonych rozmiarach

I zasada dynamiki Newtona

Ciało, na które nie działają żadne siły lub działające siły się równoważą, porusza się ruchem jednostajnym prostoliniowym lub pozostaje w spoczynku.

II zasada dynamiki Newtona

Ciało, na które działa siła niezrównoważona porusza się względem inercjalnego układu odniesienia ruchem przyśpieszonym, z przyspieszeniem proporcjonalnym do odwrotności tej siły, skierowanym i zwróconym tak samo jak działająca siła. Współczynnikiem proporcjonalności jest masa ciała.

Opracowanie wyników.

1. Promień wewnętrzny rury wiskozymetru R. Błąd niepewności pomiarowej R.

l.p.	2R [mm]	R [mm]	i	i^2	s^2	s	σ	σm
1	60,40	30,200	0,162	0,02641	0,02047	0,14307	0,16520	0,08260
2	59,70	29,850	-0,188	0,03516
3	59,90	29,950	-0,088	0,00766
4	60,30	30,150	0,112	0,01266
Rśr		30,038

R=30,038
0,083 [mm]

2. Niepewność pomiarowa wagi laboratoryjnej wynosi
0,01 [mg]

L.p.	mk[mg]
1	242,0
2	249,2
3	198,0
4	261,8
5	263,2
6	239,0
7	217,8
8	244,6
9	269,0
10	228,6

3. wartości średnie promieni kulek. Błąd pomiaru.

l.p.	2r1 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,99	2,995	0,003	0,00001	0,00007	0,00850	0,01041	0,00601
2	5,96	2,980	-0,012	0,00014
3	6,00	3,000	0,008	0,00007
rśr		2,992

r₁=2,992
0,006 [mm]

l.p.	2r2 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,88	2,940	0,002	0,00000	0,00004	0,00624	0,00764	0,00441
2	5,86	2,930	-0,008	0,00007
3	5,89	2,945	0,007	0,00004
rśr		2,938

r₂=2,938
0,0044 [mm]

l.p.	2r3 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,90	2,950	0,228	0,05214	0,02657	0,16301	0,19965	0,11527
2	5,27	2,635	-0,087	0,00751
3	5,16	2,580	-0,142	0,02007
rśr		2,722

r₃=2,722
0,1153 [mm]

l.p.	2r4 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,97	2,985	0,007	0,00004	0,00017	0,01312	0,01607	0,00928
2	5,92	2,960	-0,018	0,00034
3	5,98	2,990	0,012	0,00014
rśr		2,978

r₄=2,985
0,0093 [mm]

l.p.	2r5 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	6,00	3,000	0,032	0,00100	0,00054	0,02321	0,02843	0,01641
2	5,92	2,960	-0,008	0,00007
3	5,89	2,945	-0,023	0,00054
rśr		2,968

r₅=2,968
0,0164 [mm]

l.p.	2r6 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	6,00	3,000	0,028	0,00080	0,00041	0,02014	0,02466	0,01424
2	5,92	2,960	-0,012	0,00014
3	5,91	2,955	-0,017	0,00028
rśr		2,972

r₆=2,972
0,0142 [mm]

l.p.	2r7 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,84	2,920	-0,023	0,00054	0,00029	0,01700	0,02082	0,01202
2	5,92	2,960	0,017	0,00028
3	5,90	2,950	0,007	0,00004
rśr		2,943

r₇=2,943
0,012 [mm]

l.p.	2r8 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,57	2,785	-0,073	0,00538	0,00404	0,06355	0,07784	0,04494
2	5,70	2,850	-0,008	0,00007
3	5,88	2,940	0,082	0,00667
rśr		2,858

r₈=2,858
0,045 [mm]

l.p.	2r9 [mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,91	2,955	-0,005	0,00003	0,00005	0,00707	0,00866	0,00500
2	5,94	2,970	0,010	0,00010
3	5,91	2,955	-0,005	0,00003
rśr		2,960

r₉=2,96
0,005 [mm]

l.p.	2r10[mm]	r1[mm]	i	i^2	s^2	s	σ	σm
1	5,98	2,990	0,022	0,00047	0,00027	0,01650	0,02021	0,01167
2	5,90	2,950	-0,018	0,00034
3	5,93	2,965	-0,003	0,00001
rśr		2,968

r₁₀=2,968
0,0117 [mm]

4. Wartości średnie opadania kulek V_k. Błąd V_k.

S=0.4 [m]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,3

0,1739

-5,21E-03

2,71E-05

2,71E-05

5,21E-03

0,0073672

0,0052094

2

2,17

0,1843

5,21E-03

2,71E-05

Vkśr

0,1791

V_k1=0,1791
0,00521 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,29

0,1747

-3,83E-04

1,47E-07

1,47E-07

3,83E-04

0,0005417

0,0003831

2

2,28

0,1754

3,83E-04

1,47E-07

Vkśr

0,1751

V_k2=0,1751
0,00038 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,36

0,1695

4,10E-03

1,68E-05

1,68E-05

4,10E-03

0,0057991

0,0041006

2

2,48

0,1613

-4,10E-03

1,68E-05

Vkśr

0,1654

V_k3=0,1654
0,0041 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,27

0,1762

-4,06E-03

1,65E-05

1,65E-05

4,06E-03

0,0057419

0,0040602

2

2,17

0,1843

4,06E-03

1,65E-05

Vkśr

0,1803

V_k4=0,1803
0,00406 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,21

0,1810

-4,11E-04

1,69E-07

1,69E-07

4,11E-04

0,0005817

0,0004114

2

2,20

0,1818

4,11E-04

1,69E-07

Vkśr

0,1814

V_k5=0,1814
0,0004114 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,25

0,1778

1,17E-03

1,37E-06

1,37E-06

1,17E-03

0,0016541

0,0011696

2

2,28

0,1754

-1,17E-03

1,37E-06

Vkśr

0,1766

V_k6=0,1766
0,00117 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,38

0,1681

1,05E-03

1,09E-06

1,09E-06

1,05E-03

0,0014794

0,0010461

2

2,41

0,1660

-1,05E-03

1,09E-06

Vkśr

0,1670

V_k7=0,167
0,001046 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,19

0,1826

-1,70E-03

2,89E-06

2,89E-06

1,70E-03

0,0024028

0,0016991

2

2,15

0,1860

1,70E-03

2,89E-06

Vkśr

0,1843

V_k8=0,1843
0,0017 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,03

0,1970

7,20E-03

5,18E-05

5,18E-05

7,20E-03

0,0101795

0,0071980

2

2,19

0,1826

-7,20E-03

5,18E-05

Vkśr

0,1898

V_k9=0,1898
0,00719 [m/s]

l.p.

S [m]

t [s]

Vk[m/s]

i

i^2

s^2

s

σ

σm

1

0,4

2,37

0,1688

-4,90E-03

2,40E-05

2,40E-05

4,90E-03

0,0069262

0,0048975

2

2,24

0,1786

4,90E-03

2,40E-05

Vkśr

0,1737

V_k10=0,1737
0,00489 [m/s]

5. Prędkość graniczna dla naczynia o nieskończonych rozmiarach.

;
;

;
;

;

;

;

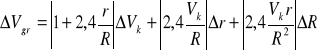
6. Wartość współczynnika lepkości .

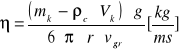
gdzie:

m_k - masa kulki

ρ_c - gęstość cieczy

V_k - objętość kulki

r - promień kulki

g - przyspieszenie ziemskie

v_gr - prędkość graniczna kulki w cieczy o nieograniczonych rozmiarach

Gęstość gliceryny w temp. 20⁰C=1,26*10³ kg/m³

8. Niepewność pomiarowa .

Lp		i	i^2	s^2	s	σ	σm
1	0,0789	-0,00884	0,00008	0,00010	0,01011	0,01065	0,00337
2	0,0944	0,00666	0,00004
3	0,0872	-0,00054	0,00000
4	0,0951	0,00736	0,00005
5	0,0981	0,01036	0,00011
6	0,0808	-0,00694	0,00005
7	0,0715	-0,01624	0,00026
8	0,0979	0,01016	0,00010
9	0,0994	0,01166	0,00014
10	0,0741	-0,01364	0,00019
śr	0,0877

87,7
0,34 [*10^-3 kg m^-1 s^-1]

Dyskusja błędów.

Średni współczynnik lepkości 87,7
0,34 [*10^-3 kg m^-1 s^-1]. Wartość tego współczynnika odczytana z tablic wynosi  [*10^-3 kg m^-1 s^-1]. Oba te współczynniki lepkości znacznie różnią się od siebie. Ta różnica może być spowodowana źle określoną drogą po której kulka poruszała się ruchem jednostajnym. Istotny wpływ na błąd ma mierzony za pomocą stopera czas trwania ruchu na drodze S.

1

7

---