Grzegorz Szalacha L 02

ĆWICZENIE 9

Sprawdzanie równania ruchu obrotowego brył

I. Zagadnienia do samodzielnego opracowania

Wielkości charakterystyczne w ruchu postępowym to :

droga s,

prędkość v=ds/dt ,

przyspieszenie a=dv/dt,

masa m,

pęd p=mv ,

siła F=ma

Wielkości charakterystyczne w ruchu obrotowym to :

kąt ,

prędkość kątowa =d/dt ,

przyspieszenie kątowe =d/dt ,

moment bezwładności I=mr2

kręt (moment pędu) K=mvr,

moment siły M=dK/dt

II. Część teoretyczna ćwiczenia.

Równanie ruchu obrotowego bryły ma postać

gdzie : I - moment bezwładności ,

- przyspieszenie kątowe.

W omawianym przypadku moment siły wyraża się wzorem:

gdzie : r - ramię siły, czyli promień tej części walca na którą nawija się nić,

m - masa ciężarka,

g - przyspieszenie ziemskie.

Moment bezwładności układu I równy jest sumie stałej części momentu Io i momentu walców W; przy czym moment bezwładności walców W zgodnie z prawem Steinera wynosi:

4 I1 + 4 MR2

gdzie: I1 - moment bezwładności walca W względem osi przechodzącej przez środek ciężkości i równoległej do osi obrotu przyrządu,

M - masa walca W

R - odległość środka ciężkości walca od osi obrotu.

Ze względów praktycznych odległość R zastępujemy odległościa przeciwległych walców d (d = 2R). Zatem całkowity moment bezwładności wyraża się wzorem :

I = I0 + 4 I1 + Md2

Pierwsze dwa wyrazy po prawej stronie tego wyrażenia są wielkościami stałymi. Wprowadzamy więc oznaczenie: Ic =I0 + 4 I1

i otrzymujemy I = Ic + Md2 .

Łącząc powyższe równania otrzymujemy:

Ze względu na to, że wektory
i
są prostopadłe do osi obrotu, a wektor
jest do niej równoległy, w powyższym równaniu możemy zaniedbać znaki wektorów.pamiętając że = a/r gdzie a = 2h/t2 i wykonując ponadto przekształcenia algebraiczne otrzymujemy:

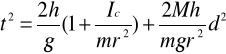
W układzie współrzędnych, w którym na osi y odkładamy t2 , a na osi x d2 , równanie powyższe jest równaniem prostej typu:

y = a + bx

a =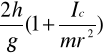

daje wartość rzędnej w punkcie, w którym prosta przecina oś rzędnych. Stromość otrzymanej prostej wyraża się poprzez :

b =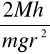

Prostoliniowy przebieg zależności t2 = f( d2 ) jest dowodem słuszności równania ruchu obrotowego bryły. Zależność tę wyznaczamy doświadczalnie.

III.Wykonanie ćwiczenia.

1. Właczyć przyrząd do sieci.

2. Przemieścić ciężarki w górę nawijając nitkę na szpulkę.

3. Wyzerować wskazania zegara.

4. Zwolnić ciężarki.

Tabela pomiarowa:

Lp	M	m	r	d	d2	t	t2	I	Ic
-	[ g ]	[ g ]	[ cm ]	[ cm ]	[ cm2 ]	[ s ]	[ s2 ]

h =43 cm

1						6.711	45,037
2						6.574	43,217
3				50	2500	6.453	41,641	6.81 * 10-2
4						6.435	41,409
5						6.804	46,294
1						6.116	37,405
2						5.810	33,756
3				44	1939	5.774	33,339	5.46 * 10-2
4						6.064	36,772
5						5.840	34,105
1						5.051	25,512
2						5.020	25,2
3	240	4x193	4	38	1444	4.870	23,716	4.28 * 10-2	8.14 * 10 -3
4						4.924	24,245
5						5.065	25,654
1						4.221	17,816
2						4.132	17,079
3				32	1024	4.276	18,290	3.27 * 10-2
4						4.101	16,823
5						4.413	19,480
1						3.918	15,356
2						3.844	14,776
3				26	676	3.805	14,478	2,44 * 10-2
4						3.803	14,462
5						3.820	14,592
1						3.195	10,208
2						3.147	9,903
3				20	400	3.101	9,616	1.77 * 10-2
4						3.121	9,740
5						3.144	9,884
1						2.656	7,054
2						2.740	7,507
3				14	196	2.714	7,365	1.28 * 10-2
4						2.595	6,734
5						2.677	7,166

h = 30 cm

1						5.348	28,601
2						5.377	28,912
3				50	2500	5.395	29,106	7.22 * 10-2
4						5.422	29,398
5						5.406	29,224
1						4.653	21,650
2						4.672	21,827
3				42	1764	4.572	20,903	5.45 * 10-2
4						4.605	21,206
5						4.569	20,875
1						4.166	17,355
2						4.055	16,443
3				34	1156	4.175	17,430	3.99 * 10-2	1.22 * 10 -2
4						4.093	16,752
5						3.978	15,824
1						3.244	10,523
2						3.333	11,108
3				26	676	3.173	10,067	2.84 * 10-2
4						3.253	10,582
5						3.312	10,969
1						2.576	6,635
2						2.534	6,421
3				18	324	2.409	5,803	1.99 * 10-2
4						2.477	6,135
5						2.601	6,765

h = 43 cm

tśr (dla d=50) = 6,59

tśr2 = 43,5

tśr (dla d=44) = 5,92

tśr2 = 35,05

tśr (dla d=38) = 4,98

tśr2 = 24,86

tśr (dla d=32) = 4,23

tśr2 = 17,88

tśr (dla d=26) = 3,84

tśr2 = 14,73

tśr (dla d=20) = 3,14

tśr2 = 9,87

tśr (dla d=14) = 2,67

tśr2 = 7,16

h = 30 cm

tśr (dla d=50) = 5,39

tśr2 = 29,05

tśr (dla d=42) = 4,61

tśr2 = 21,29

tśr (dla d=34) = 4,09

tśr2 = 16,75

tśr (dla d=26) = 3,26

tśr2 = 10,65

tśr (dla d=18) = 2,52

tśr2 = 6,34

Rysuję wykres zależności t2 = f(d2)

Określam błąd :

(d2) = 2* d *d

d = 0.2 (błąd ustawienia ciężarków)

(502)=2*50*0.2 = 20 i przyjmuję go jako błąd (d2)

Określam błąd:

(t2) = 2*t*t

t=0.2 s (błąd związany z niedokładnością pomiaru )

(6.592) = 2*6.59*0.2 = 2.636

Odczytuję z wykresu a oraz b, i obliczam moment bezwładności Ic oraz masę walca M.

a = 0.666

b = t2/d2=0.01162

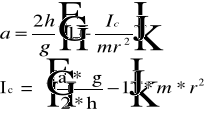
Ic = 1.22 * 10 -2 dla h = 30 cm

Ic = 8.14 * 10 -3 dla h = 43 cm

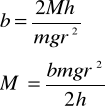
Po podstawieniu

M = 245 g

M = 234 g

Przyjmuję M = 240 g

Aby obliczyć I stosuję wzór :

I = Ic + Md2

h =43 cm

I(d=50) = 6.81 * 10-2

I(d=44) = 5.46 * 10-2

I(d=38) = 4.28 * 10-2

I(d=32) = 3.27 * 10-2

I(d=26) = 2,44 * 10-2

I(d=20) = 1.77 * 10-2

I(d=14) = 1.28 * 10-2

h = 30 cm

I(d=50) = 7.22 * 10-2

I(d=42) = 5.45 * 10-2

I(d=34) = 3.99 * 10-2

I(d=26) = 2.84 * 10-2

I(d=18) = 1.99 * 10-2

V. Wnioski

Masa otrzymana przez nas jest trochę większa od rzeczywistej. Przyczyną tego jest błąd systematyczny jaki popełnialiśmy przy mierzeniu odległości walców.

---