DŁUGI

Oznaczenia stosowane przy rozliczaniu długów:

S - wartość początkowa długu;

N - liczba rat umarzających dług;

T_n - n-ta rata długu, n-ta rata kapitałowa, część długu spłacana w n-tej racie łącznej, n=1, 2, …,N;

Z_n - n-ta rata odsetkowa, wartość odsetek spłacana w n-tej racie łącznej,
n=1, 2, …,N; Z_n=S_n-1r

A_n - n-ta rata łączna (spłata, płatność), A_n=T_n+Z_n;

S_n - pozostała część długu po spłaceniu n rat, dług bieżący, S₀=S;

Z - suma wartości nominalnych wszystkich rat odsetkowych, Z=Z₁+…Z_N=(A₁+…A_N)-S.

S=T₁+…+T_N

PLAN SPŁATY DŁUGÓW ŚREDNIO- I DŁUGOTERMINOWYCH

SPŁATA DŁUGU O ZADANYCH RATACH ŁĄCZNYCH ZGODNA

, n=1, 2, …, N

Z_n=S_n-1r; n=1, 2, …,N

T_n=A_n-Z_n=S_n-1-S_n; n=1, 2, …,N

Z=Z₁+…Z_N=(A₁+…+A_N) -S

RATY ŁĄCZNE O RÓWNYCH WYSOKOŚCIACH - spłaty zgodne

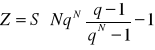
RATY ŁĄCZNE O RÓWNYCH WYSOKOŚCIACH - spłaty niezgodne

okres spłat jest równy okresowi kapitalizacji

spłaty częstsze niż kapitalizacja

oraz

kapitalizacja częstsza niż spłaty

…

SPŁATA DŁUGU O ZADANYCH RATACH KAPITAŁOWYCH - ZGODNA

Z_n=S_n-1r

A_n= T_n +Z_n

Z=Z₁+…Z_N=(A₁+…+A_N) -S

RATY KAPITAŁOWE O RÓWNYCH WYSOKOŚCIACH - spłaty zgodne

RATY KAPITAŁOWE O RÓWNYCH WYSOKOŚCIACH - spłaty niezgodne

Okres spłat równy okresowi kapitalizacji

• 
  ,
  

• 
  

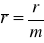
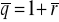
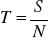
Spłaty częstsze niż kapitalizacja

W odniesieniu do pełnych okresów:

, (n=1, 2, …, N)

W odniesieniu do podokresów:

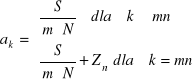
kapitalizacja częstsza niż spłaty

KREDYTY Z DODATKOWĄ OPŁATĄ

A_n=T_n+Z_n+G_n

Wysokość opłaty G_n:

• wartości części spłacanego długu T_n

G_n =T_n p

gdy
to
, (n=1, 2, …, N)

gdy A₁=A₂=…=A_N=A oraz
to

oraz

• reszty niespłaconego długu S_n-1

G_n =S_n-1 p

gdy
to
, (n=1, 2, …, N)

A_n=T_n+Z_n+G_n=T_n+ S_n-1(r+p)

.

gdy A₁=A₂=…=A_N=A to

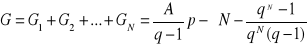
MATEMATYKA FINANSOWA WYKŁAD 4 i 5 1

Dr Anna Górska

---