Siły bezwładności unoszenia:

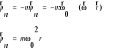
Siła bezwładności Coriolisa

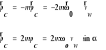
Równanie dynamiczne ruchu względnego:

Geometria mas. Teoria momentu bezwładności

1)Układ punktów materialnych- zbiór złożony z dowolnej liczby punktów materialnych o masach m1,m2,m3,…. których położenie definiują promienie - wektory r1,r2,r3,r4,… poprowadzone z dowolnie dobranego bieguna 0. Następnie wprowadźmy nieruchomy układ współrzędnych {0,x,y,z} o początku w biegunie 0.

2)Środek masy układu punktów materialnych - punkt którego promień wektor opisuje równanie:

3)Moment statyczny- układ punktów materialnych względem płaszczyzny x=0

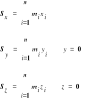
4)Moment bezładności ciała materialnego(ciało materialne- zbiór punktów o masach dm).

5)momenty bezwładności ciała względem osi 0Z:

p- gęstosć rozkładu masy

h- odległość od osi

6)Momenty bezwładności względem płaszczyzn:x=0,y=0,z=0,

analogicznie dla y=0,z=0

Moment bezwładności względem osi to suma momentów bezwładności względem płaszczyzn przeciągających się wzdłuż tej osi,

7)Biegunowy moment bezwładności:

8)Promienie bezwładności:

9)Momenty bezwładności niektórych przypadków:

a)cienki pręt:

b)Jednorodny walec:

c)cienka tarcza

d)kula

10)moment bezwładnościowe względem osi równoległych tw. Steinera

11)Moment odśrodkowy (zboczeniowy)

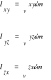
PED UKŁADU PUNKTÓW MATERIALNYCH

1)Siły działające na układ:

- zewnętrzne

- wewnętrzne

2)PĘD- jest to wielkość:

Lub ilość ruchu układu punktów materialnych (twierdzenie o pedzie):

KRĘT UKŁADU PUNKTÓW MATERIALNYCH

1)Kręt-momentem pędu punktu o masie m względem nieruchomego bieguna 0 nazywamy wielkość:

Gdzie: r- promień-wektor punktu

v- prędkość punktu

2)Kręt układu punktów:

Wypadkowa sił zewnętrznych na punkty o masie m

Wypadkowa sił wewnętrznych na punkty o masie m

dla i=1,2,3,4…..

Uwaga:

Zatem:

Oznaczenia:

1) Kręt układu punktów materialnych względem bieguna 0

2)Moment i-tej siły zewnętrznej

Ponieważ:

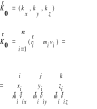
Zatem:

Dwa przypadki szczególne:

a)Ruch postępowy układu punktów materialnych:

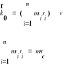
promień-wektor środka masy

Zatem:

b)Jednostajny ruch obrotowy:

Kręt elementowy względem osi OZ:

Gdzie: h- ramie pędu

Zatem:

Przykład:

Ciało sztywne z siłami ciężkości obracające się wokół osi pionowej OZ w idealnie gładkich łożyskach:

Moment bezwładności podczas ruchu ulega zmianie:

ZASADA D'ALEMBERTA

Dla punktów materialnych o mase m równanie dynamiczne ruchu ma postać:

Pierwszy człon to siły bezwładne,

Drugi człon to siły rzeczywiste,

WEKTOROWE RÓWNANIA RÓWNOWAGI DLA ŚRODKA MASY UKŁADU PUNKTÓW MATERIALNYCH

a)siły:

b)momenty:

UWAGA:

RUCH POSTĘPOWY CIAŁA SZTYWNEGO:

Na ciało działają siły zewnętrzne: P1,P2,P3,….Pi

przyśpieszenie środka masy

układ poruszający się ruchem postępowym razem z ciałem

Określić:

a)przyśpieszenie środka masy

b)warunek jaki musza spełniać siły P1… aby ciało poruszało się ruchem postępowym

Analiza:

Z zasady d'Alemberta:

Wypadkowe przyśpieszenie:

Kąt:

RUCH OBROTOWY CIAŁA SZTYWNEGO

Obrót wokół osi OZ, siły zewnętrzne P1,P2,P3…

prędkość kątowa

przyśpieszenie katowe

z TW. O kręcie:

(*)

Gdzie:

moment siły Pi względem OZ

moment główny względem osi OZ wszystkich sił Pi

Mamy:

Zatem równanie * ma postać:

Z (1) i (2) otrzymujemy równanie dynamiczne ruchu ciała obrotowego :

RÓWNANIE DYNAMICZNE RUCHU PŁASKIEGO CIAŁA SZTYWNEGO:

przyśpieszenie środka masy

siły zewnętrzne działające na ciało

Z TW o środku masy:

Z TW o kręcie względem środka:

Ale:

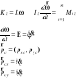
Zatem ostatecznie, równania ruchy płaskiego:

ENERGIA KINETYCZNA UKŁADU PUNKTÓW MATERIALNYCH

a) ruch postępowy

b)ruch obrotowy

TWIERDZENIE KOENIGA

Mamy dwa układy współrzędnych:

układ nieruchomy

układ ruchomy względem układu odniesienie

Rozkładamy wektor prędkości Vi na:

A więc:

Zatem :

Ostatecznie

Gdzie:

ENERGIA KINETYCZNA W PRZYPADKU OGÓLNEGO WUCHU CIAŁA SZTYWNEGO

Zatem:

TWIERDZENIE O ENERGI KINETYCZNEJ UKŁADU PUNKTÓW MATERIALNYCH I CIAŁA SZTYWNEGO

a)układ punktów materialnych

przyrost energii kinetycznej

suma prac siły zewnętrznych

suma prac sił wewnętrznych

b)ciało sztywne

RUCH KULISTY I RUCH OGÓLNY CIAŁA SZTYWNEGO

1)Kręt i energia w ruchu kulistym ciała sztywnego

Zatem dla trzech współrzędnych:

(*)

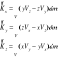
Ruch kulisty jest chwilowym ruchem obrotowym

Zatem:

Gdzie omega to prędkość chwilowa obrotowa

Podstawiamy do * i ostatecznie otrzymujemy:

Osie x,y,z są głównymi osiami bezwładności punktu

Energia Kinetyczna:

RÓWNANIE DYNAMICZNE EULERA:

układ współrzędnych osi poruszające się z ciałem

Ko-kręt działający na ciało

Składowe kretu układu osi głównych

Pochodna wzgledna i bezwzględna dowolnego wektora:

Dla Kretu:

Ponieważ

Otrzymujemy równania dynamiczne Eulera