Laboratorium z Teorii sygnałów

Ćw. 4 i 5

Generacja i splot sygnałów.

Dyskretna transformata Fouriera i splot kołowy.

Sprawozdanie wykonał:

Piotr Żytkowski

Gr. E5 sekcja 21

Zadania do wykonania przed laboratorium:

a)wyznaczyć splot y(n)=x₁(n)*x₂(n) następujących sygnałów dyskretnych:

x₁(n)= 0,9ⁿ dla n od 0....4 i x₁(n)=0 dl n>4

x₂(n)=1 dla n od 0..6 i x₂(n)=0 dla n>6

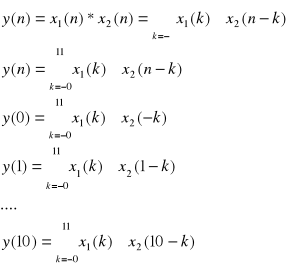
Na podstawie powyższych równań wyznaczono następujące wartości:

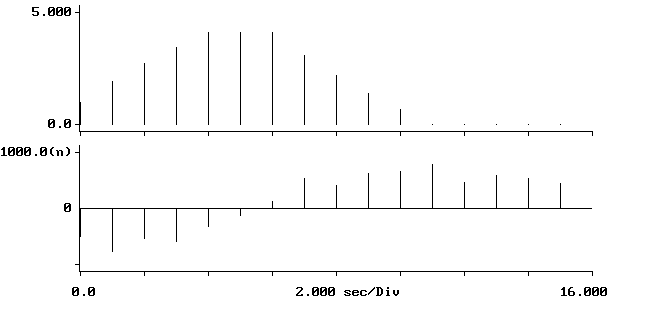
y(0)=1 y(1)=1,9 y(2)=2,71 y(3)=3,439 y(4)=4,0951 y(5)=4,0951

y(6)=4,0951 y(7)=3,0951 y(8)= 2,1951 y(9)=1,3851 y(10)=0,6561

b) wykazać, że splot dyskretny jest przemienny tzn. x₁(n)*x₂(n) =x₂(n)*x₁(n)

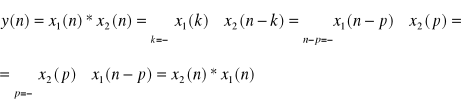
Zadanie 1: Splot dwóch impulsów prostokątnych:

Splot liniowy dwóch sygnałów dyskretnych x₁(n) i x₂(n) jest sygnałem dyskretnym y(n) określonym następująco:

Zawężenie przedziału sumowania ze względu na skończony czas

trwania x₁(n) i x₂(n):

y(8)= y

Liczba niezerowych próbek splotu liniowego y(n) wynosi: N_y=N_x1+N_x2-1 (w szczególności N_y=2N-1, jeżeli N=N_x1=N_x2).

1. splot gdy x₁(n)=x₂(n)

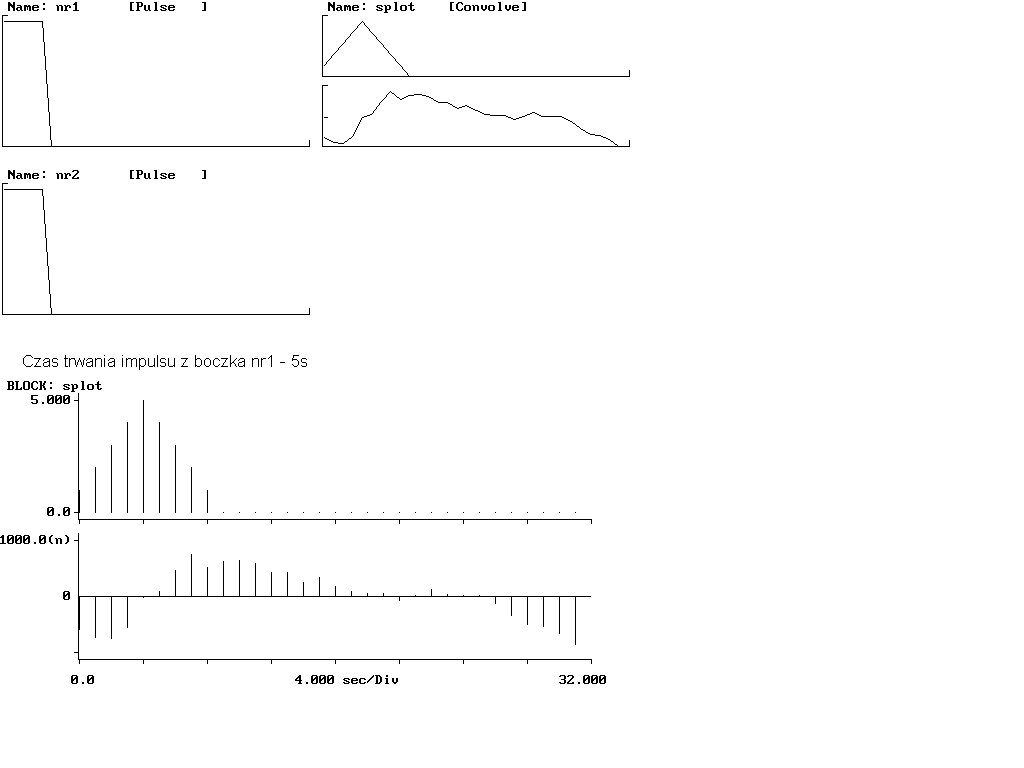
2. splot gdy x₁(n)=2x₂(n) i x₁(n)=3x₂(n)

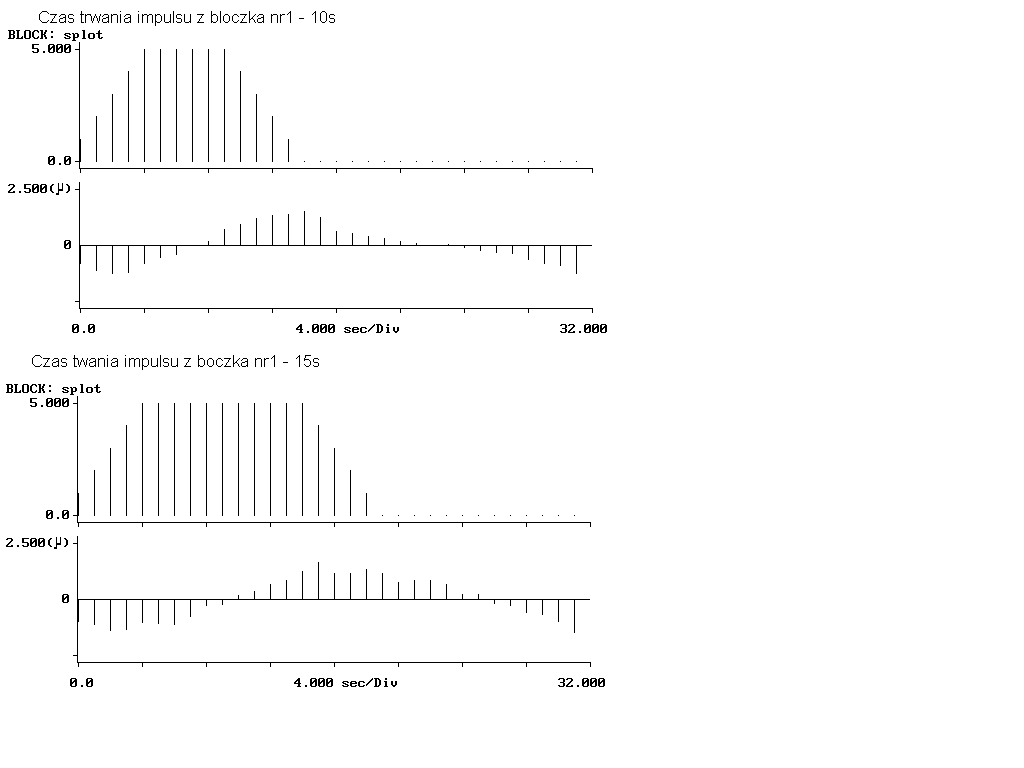
Na ekranie pojawiły się dwa rysunki: część rzeczywista i część urojona sygnału powstałego w rezultacie splotu dwóch impulsów prostokątnych. Szczątkowy (rzędu piko) sygnał urojony wynika z wykonania splotu w dziedzinie częstotliwości i kumulacji błędu obliczeń - splot dwóch sygnałów czysto rzeczywistych ma charakter czysto rzeczywisty.

Zgodnie z tym co napisałem na początku liczba niezerowych próbek splotu liniowego wynosi: N_x1=N_x2=5 wtedy N_y=9

N_x1=10 i N_x2=5 wtedy N_y=14

N_x1=15 i N_x2=5 wtedy N_y=19

Zadanie 2: Próbkowanie sygnału z generatora za pomocą programu AClab.

Zgodnie z twierdzeniem Kottelnikowa-Shannona-Nyguista - sygnał, którego widmo jest ograniczone do w_m można odtworzyć na podstawie próbek pobieranych z częstotliwością Ω₀ nie mniejszą niż 2w_m.

Po przekroczeniu częstotliwości ok. 5kHz mmy do czynienia z zjawiskiem aliasingu (powielone widma sygnału analitycznego zachodzą na siebie i widmo sygnału dyskretnego nie przypomina sygnału analogowego. Natomiast dla częstotliwości 10kHz otrzymujemy sygnał sinusoidalny, jednak nie jest to sygnał podany na wejście - jest to sygnał, którego częstotliwość jest różnicą pomiędzy częstotliwością próbkowania i częstotliwością sygnału próbkowanego.

Ćwiczenie 5

Zadania do wykonania przed ćwiczeniem:

1. Jaka jest zależność pomiędzy długością ciągu wejściowego N, a liczbą operacji arytmetycznych niezbędnych do wyznaczenia dyskretnej transformaty Fouriera oraz szybkiej transformaty Fourier?

Obliczenie DFT wymaga sporego nakładu obliczeń. Dla rzeczywistego ciągu x(n), wyznaczenie N- punktowej transformaty wymaga wykonania 2N² mnożeń rzeczywistych. W przypadku ciągu zespolonego liczba t wynosi 4 N² (co odpowiada N² mnożeń liczb zespolonych). Oprócz mnożeń trzeba wykonać N(N-1) sumowań liczb zespolonych.

Natomiast przy FFT zamiast wyznaczania transformaty N punktowej wyznaczamy dwie transformaty N/2 punktowe, przez co uzyskujemy wyraźną oszczędność nakładu obliczeń:

Obliczenie dwóch transformat N/2 punktowych wymaga wykonania 2(N/2)² mnożeń - dwukrotnie mniej niż w przypadku DFT N- punktowej. Jeżeli potrafimy zastąpić obliczenie transformaty N - punktowej transformatą N/2 punktową, to możliwe jest także kontynuowanie takiego podejścia tzn. obliczenie coraz krótszych transformat N/4, N/8 itd.

2. Jakie warunki musi spełniać sygnał x(n), by jego DFT była czysto rzeczywista lub czysto urojona?

Aby X(k) było liczbą rzeczywistą niezależnie od k, sygnał x(n) musi dać się przedstawić w postaci:

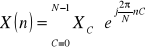
gdzie: X_C - dowolna liczba rzeczywista

Dowód:

,

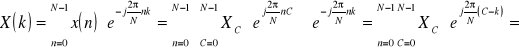
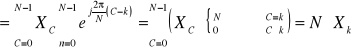
Aby transformata była czysto urojona, sygnał x(n) musi być wyrażony w postaci:

Dowód jest analogiczny do obliczeń przedstawionych dla transformaty czysto rzeczywistej.

Zadanie2: dyskretna i szybka transformata Fouriera.

a)

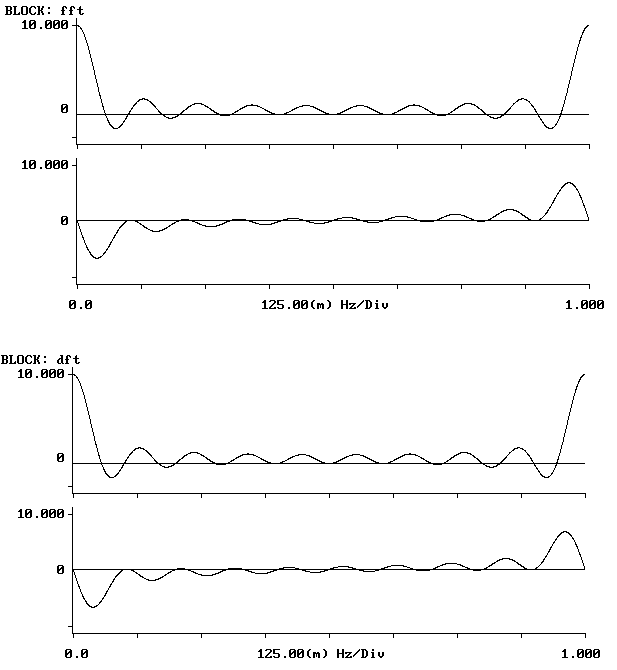
Wyniki obliczeń są jednakowe. Jednak przy badaniu 2048 próbek dokładnie widzimy różnię pomiędzy DFT i FFT - obliczenia FFT zajmują ok. 1s, natomiast obliczenie DFT zajmuje ok.15s.

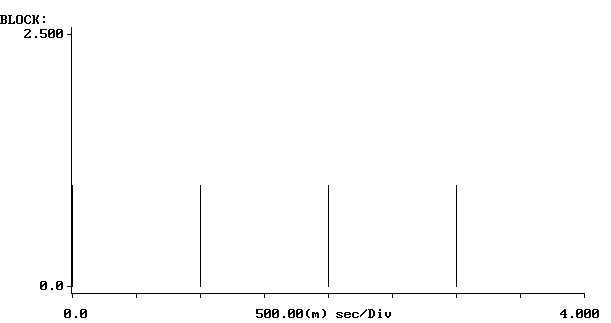
b) x(n)=1 dla n od 0...3 i x(n)=0 dla n>0

sygnał wejściowy

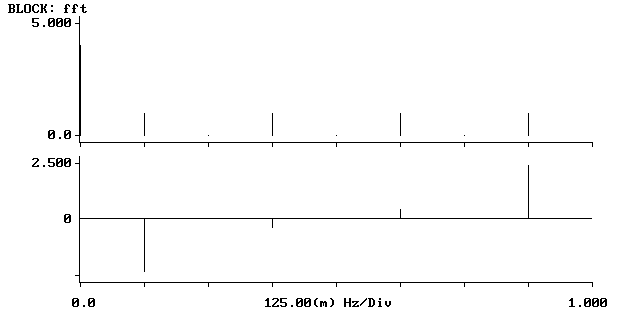
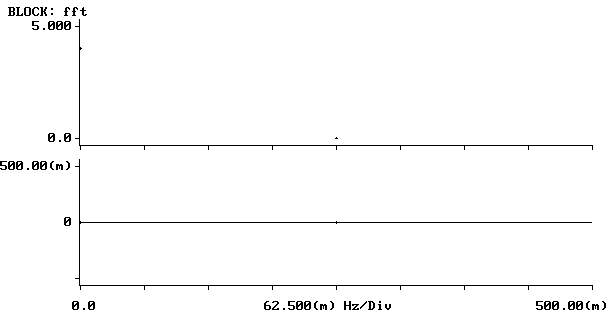
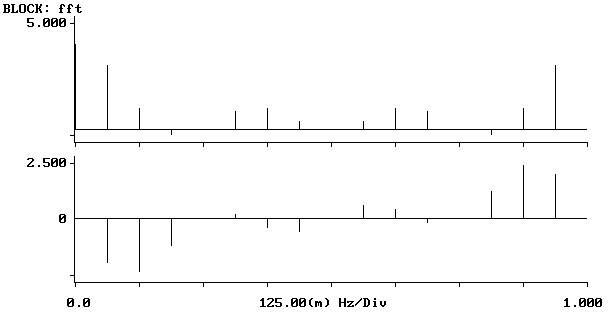
Transformata 4-punktowa Transformata 8-punktowa

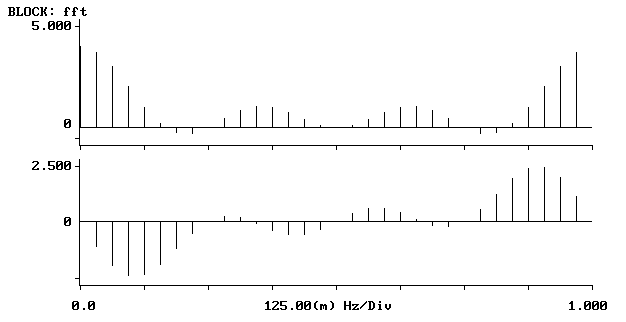
Transformata 16-punktowa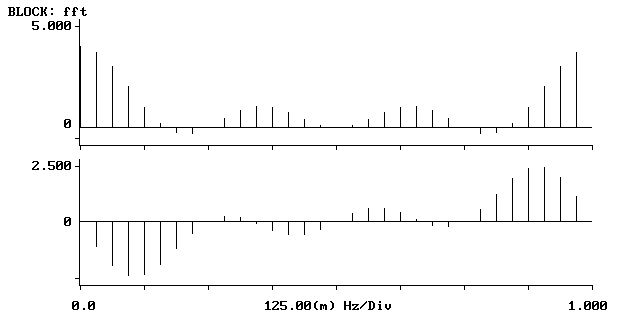
Transformata 32-punktowa

Transformata 64-punktowa

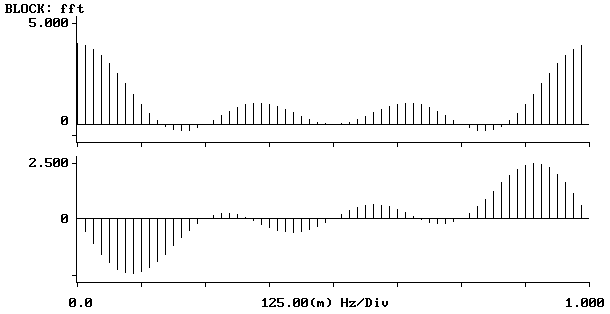
Jak widzimy z przebiegów zamieszczonych powyżej w miarę wzrostu liczby punktów transformaty dyskretne widmo ulega zagęszczeniu. Obserwowane wykresy zdążają w kierunku transformaty ciągłej sygnału dyskretnego.

c) porównanie 128-punktowych transformat idealnych sygnałów cosinusoidalnych o częstotliwościach 0,125Hz i 0,123Hz.

- sygnałów cosinusoidalny o częstotliwości 0,125Hz

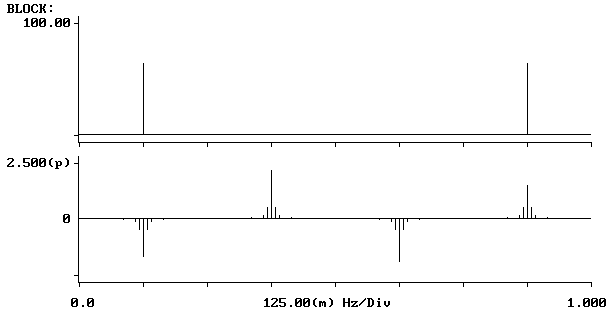
• sygnałów cosinusoidalny o częstotliwości 0,123Hz

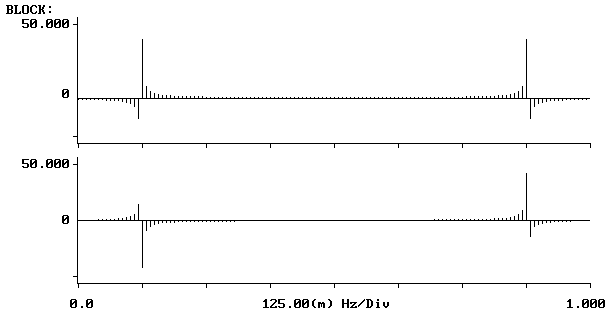
Dla częstotliwości sygnału 0.125 Hz oraz częstotliwości próbkowania 1 Hz, pierwsze 128 próbek to dokładnie 16 okresów sygnału wejściowego. Zachowana jest ciągłość (kształtu) sygnału pomiędzy ostatnią i pierwszą próbką. Obserwujemy dwa prążki o częstotliwościach 0.125 Hz i 0.875 Hz. Prążek o częstotliwości 0.125 Hz to składowa widma sygnału wejściowego, natomiast prążek o częstotliwości 0.875 Hz to składowa kopii widma sygnału wejściowego utworzona w procesie próbkowania (0.875 = 1-0.125).

Dla częstotliwości sygnału wejściowego 0.123 Hz, pierwsze 128 próbek to niecałe 16 okresów tego sygnału. Nie jest zachowana ciągłość kształtu pomiędzy ostatnią i pierwszą próbką, co objawia się w postaci dodatkowych niezerowych prążków widma. Zjawisko to nazywane jest przeciekiem widma.

Zadanie3: Uzupełnianie sygnału zerami.

1. sygnał cos 0,125Hz

2. sygnał cos 0,123Hz

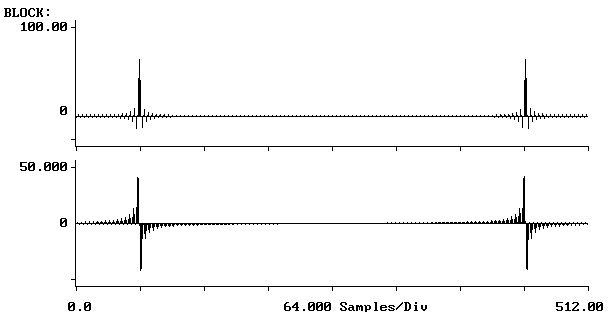
Widmo sygnału 0,125Hz w porównaniu do widma sygnału nie uzupełnionego zerami charakteryzuje się dodatkowymi prążkami o niezerowej amplitudzie.

Jeżeli zmieni się częstotliwość funkcji cosinus na 0.123 Hz to otrzymane w ten sposób widmo nie różni się praktycznie od widma cos 0.125Hz uzupełnionego zerami.
W obydwu przypadkach pojawiają się dodatkowe prążki poza prążkiem odpowiedniego cosinusa.

3. 512-punktowa transformata nieokresowego impulsu o długości 128 próbek

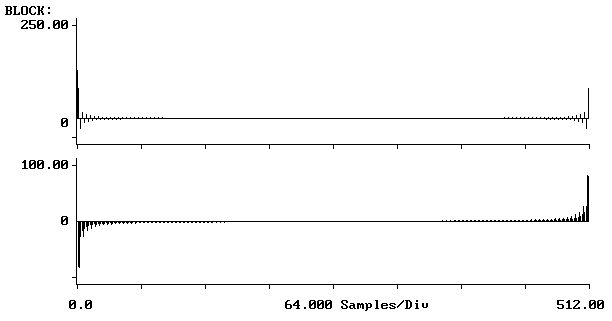
W wyniku porównania cosinusa 0,125Hz z impulsem prostokątnym (128 próbek uzupełnionych zerami) można zauważyć, że widma dyskretne tych sygnałów są podobne, mają one te same kształty, tylko prążki przypadają na inne częstotliwości.

d) mnożenie cosinusa przez impuls prostokątny

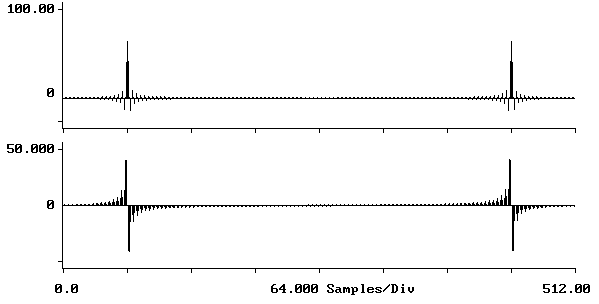
Na wyjściu układu mnożącego otrzymaliśmy sygnał identyczny jak w podpunkcie a) (wymnożenie przez siebie obydwu wymienionych sygnałów odpowiada dopisaniu 384 próbek zerowych do 128 próbek cosinusa). Tak więc i transformata z tego sygnału jest identyczna jak w podpunkcie a).

---