Funkcja liniowa - poziom podstawowy

Zad. 1 (3p) W tabeli podane są wartości funkcji liniowej f dla kilku argumentów :

x	-3	2	4	8	6
f(x)	-2,5	0	1	3	2

Wyznacz wzór funkcji f.

Zad. 2 (3p) Do wykresu funkcji liniowej należą punkty A(0;4), B(2;0). Sprawdź czy dla argumentu x=
wartość funkcji f jest równa 3-
.

Zad. 3 (5p) Punkty A(-4, -1), B(6;-1), C(1,4) są wierzchołkami trójkąta ABC. Trójkąt ten jest graficzną ilustracją zbioru rozwiązań pewnego układu nierówności liniowych. Zapisz ten układ nierówności.

Zad. 4 (3p) Wyznacz wzór funkcji liniowej o współczynnikach całkowitych. Wiedząc, że jej wykres przecina oś OY w punkcie A(0;5) zaś oś OX w punkcie którego odcięta jest mniejsza od -3.

Zad. 5 (3p) Dana jest funkcja f: R
R określona wzorem f(x)=(3m - 2)x + 2m - 1

a) Dla jakich wartości parametru m funkcja f jest malejąca ?

b) Dla jakich wartości parametru m miejscem zerowym funkcji jest liczba 1?

c)Dla jakich wartości parametru m kąt nachylenia wykresu funkcji f do osi OX na miarę 45^o?

Zad. 6 (3p) Dla jakich wartości x pełniony jest układ nierówności 5
f(x)
gdy f(x)=
x -
.

Zad. 7 (3p) Zaznacz w układzie współrzędnych zbiór punktów płaszczyzny, których współrzędne spełniają układ nierówności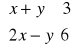

Zad. 8 (3p) Dla jakich wartości parametru m rozwiązanie układu (x_o, y_o) równań liniowych

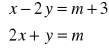
jest parą współrzędnych punktu należącego do płaszczyzny domkniętej do której należy punkt A(0,1) i której krawędź jest prostą o równaniu y = 2x.

Zad. 9 (3p) Na rysunku przedstawiony jest wykres funkcji liniowej f.

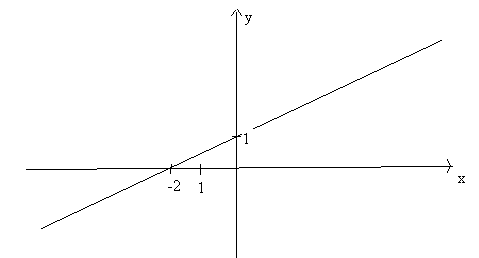
Rozwiąż nierówność 2

Zad. 10 (3p) Miara kąta nachylenia wykresu funkcji liniowej f do osi OX jest równa 135^o . Wykres funkcji f przecina oś OY w punkcie o rzędnej równej 3. Oblicz współrzędne punktu przecięcia wykresu funkcji f i wykresu funkcji określonej wzorem
g(x)= 3x -
.

Zad. 11 (6p) Współczynniki we wzorze funkcji liniowej f są liczbami całkowitymi. Dla argumentów x mniejszych od -6 wartości funkcji są ujemne. Wyznacz wzór funkcji f. Wiedząc, że f(3)

f(1)
.

Zad. 12 (4p) O funkcji liniowej f wiadomo, że przyjmuje wartości -8.

a)Napisz wzór tej funkcji i narysuj wykres.

b)Wyznacz wzór proporcjonalności prostej, której wykres jest prostopadły do wykresu funkcji f.

Zad. 13 (5p) Samochód zużywa średnio 6,8l na 100km.

a) Opisz zależność ilości zużytego paliwa do przebytej drogi i narysuj wykres tej funkcji. Czy ta funkcja jest proporcjonalnością prostą?

b)Przyjmując, że pojemność baku wynosi 55l oblicz, jaką najdłuższą drogę może przebyć ten samochód bez uzupełniania paliwa.

Zad. 14 (5p) Jakub kupił kurtkę, która wraz z 22% podatkiem VAT kosztowała 610zł.

a) Oblicz cenę kurtki bez VAT-u.

b)Jaki wzór ma funkcja wykazująca zależność miedzy cena towaru z VAT-em, a ceną bez VAT-u?

Czy to jest proporcjonalność prosta? Narysuj wykres.

Zad. 15 (5p) Jan i Zofia Wesołowscy gromadzą oszczędności na oddzielnych kontach w banku. Jeżeli mąż oddałby żonie 400zł to miałby na koncie kwotę o 14
%większą niż żona. Jeżeli natomiast żona oddałaby mężowi 400zł, to stan konta męża byłby dwa razy większy niż stan konta żony. Jakie oszczędności mają w banku Jan i Zofia?

Zad. 16 (5p) Właściciel schroniska chce kupić 75 koców. Na zakup może przeznaczyć 6500zł. Sprzedawca zaproponował dwa rodzaje koców: grube po 95zł i cienkie po 67zł za sztukę. Kupujący zdecydował się na kupno dwóch rodzajów koców, tak aby liczba koców grubych była możliwie największa. Ile koców obu rodzajów kupił właściciel schroniska?

Zad. 17 (6p) Narysuj wykres funkcji f(x)=3sgn(2x)-1 i określ jej zbiór wartości.

Zad. 18 (6p) Przeciwprostokątna trójkąta prostokątnego ABC zawiera się w prostej o równaniu x-5y+5=0, a jedna z przyprostokątnych w prostej x+y-1=0. Wierzchołkiem kąta prostego jest punkt B(3,-20).

a) Wyznacz równanie prostej zawierającej drugą przyprostokątną i znajdź pozostałe wierzchołki trójkąta. Wykonaj rysunek .

b) Opisz za pomocą nierówności zbiór punktów należących do trójkąta ABC.

Zad. 19 (6p) Państwo Nowakowie zaplanowali 6 godzinną podróż samochodem. W połowie drogi musieli zrobić nieplanowany postój, który trwał godzinę. Aby nie przekroczyć czasu 6 godzin zwiększyli prędkość o 40km/h. Z jaką średnia prędkością jechali pierwotnie i jaka była długość trasy?

Zad. 20 (6p) Wiadomo, że funkcja liniowa f przyjmuje wartości ujemne tylko dal x
, a jej wykres przechodzi przez punkt A(-1,7). Funkcja liniowa g jest proporcjonalnością prosta, której wykres jest prostopadły do prostej y=-
. Wyznacz wzory funkcji f i g, narysuj ich wykresy i odczytaj rozwiązanie nierówności f(x)
g(x).

Zad. 21 (5p) Firma produkuje samochodziki dla dzieci. Koszty produkcji w ciągu jednego miesiąca opisuje funkcja f(x)=1000+45x, gdzie 1000 jest kosztem stałym, a 45 to koszt produkcji jednego samochodziku, x to liczba samochodzików.

a) Ile samochodzików wyprodukowano w miesiącu, w którym koszt produkcji wyniósł 25300zł?

b)Jaki był zysk w miesiącu, w którym wyprodukowano 1200 samochodzików i sprzedano je po 60zł za sztukę?

Zad. 22 (5p) Dane są punkty A(1,1)i B(5,3). Wyznacz punkt C na osi OY, który jest równoległy od punktów A i B.

Zad. 23 (4p) Uczniowie zamierzają wynająć autokar na wycieczkę. Gdyby każdy z nich zapłacił 22zł to zabraknie 105zł, a jeśli każdy zapłaci 27zł to zostanie 70zł. Ile osób chce jechać na wycieczkę i jaki jest koszt wynajęcia autokaru?

Zad. 24 (6p) Dany jest odcinek o końcach A(-5,-3) B(7,-1). Wyznacz trzy punkty dzielące ten odcinek na trzy równe części.

Zad. 25 (6p) Dane są punkty A(-3,5), B(7,0), C(1,-5). Napisz równanie prostej, w której zawiera się wysokość poprowadzona z wierzchołka B oraz równanie symetralnej boku AC.

Zad. 26 (4p) Dla jakich wartości parametru m proste l:
, k :
, n:
przecinają się w jednym punkcie. Sprawdź rachunkowo, czy ten punkt należy do półpłaszczyzny określonej nierównością
.

Zad. 27 (4p) Bok AB równoległoboku ABCD jest zawarty w prostej o równaniu
, a jednym z wierzchołków jest punkt D (-3,7). Wyznacz równanie prostej zawierającej bok CD oraz bok AD jeśli wiesz, że bok AD tworzy z osią OX kąt
.

Zad. 28 (5p) Jeden z boków trójkąta równobocznego jest zawarty w osi OX, a jeden z wierzchołków to punkt O(0,0). Napisz równania prostych zawierających boki trójkąta oraz znajdź współrzędne wierzchołków jeśli wiesz, że długość boku jest równa 6.

Zad. 29 (4p) Wykaż, że punkt A
należy do prostej przechodzącej przez punkt B
i nachylonej do osi OX pod kątem
. Oblicz odległość miedzy punktami A i B.

Zad. 30 (5p) Dane są współrzędne trzech wierzchołków równoległoboku ABCD:
,
. Wyznacz współrzędne punktu D i środek symetrii równoległoboku.

Zad. 31 (4p) Wyznacz na osi OX taki punkt P, aby jego odległość od punktu
była równa
.

Zad.32 (6p) Sprawdź, czy w czworokąt o wierzchołkach
można wpisać okrąg. Znajdź parametr m tak, aby punkt
należał do prostej AC.

Zad. 33 (6p) Dla jakiej najmniejszej wartości parametru m punkt
należy do prostej l prostopadłej do prostej o równaniu
i przechodzącej przez punkt
? Oblicz odległość punktu A od osi OX.

Zad. 34 (6p) Oblicz długość środkowej trójkąta ABC poprowadzonej z wierzchołka C, jeśli
, a środek boku BC ma współrzędne
. Sprawdź czy środkowa jest prostopadła do odpowiadającego jej boku.

Zad. 35 (4p) Wykaż, że nie istnieje parametr m, taki aby proste l i k nie były równoległe gdy:

Zad.36 (5p) Dany jest wierzchołek
trójkąta ABC, środek
boku AB oraz środek
boku AC. Sprawdź rachunkowo czy kąt nachylenia boku BC do osi OX jest ostry czy rozwarty.

Zad. 37 (6p) Dany jest wierzchołek
kwadratu ABCD oraz równanie przekątnej BD:
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.

Zad. 38 (5p) Wykaż, że czworokąt o wierzchołkach
jest kwadratem.

Zad. 39 (5p) Wyznacz na osi OY punkt P równoodległy od punktów
. Oblicz pole trójkąta ABP.

Zad. 40 (4p) Wyznacz parametr m tak, aby proste l i k były prostopadłe jeśli l:
, k:

Zad. 41 (5p) Sprawdź, czy odległość punktu
od symetralnej odcinka o końcach
jest większa od 1.

Zad. 42 (6p) Dwa boki kwadratu ABCD zawarte są w wykresie funkcji
. Bok kwadratu ma długość
. Wyznacz wierzchołki tego kwadratu.

Zad. 43 (5p) Wyznacz na prostej
taki punkt C, aby suma kwadratów jego odległości od punktów
była najmniejsza. Oblicz tę odległość.

Zad. 44 (4p) Dla jakiej wartości parametru m punkt wspólny prostych
należy do II ćwiartki układu współrzędnych.

Zad. 45 (3p) Wiedząc, że punkty
są współliniowe wyznacz k.

Zad. 46 (4p) Dane są proste równolegle o równaniach
oraz
. Oblicz odległość między tymi prostymi.

Zad. 47 (3p) Odcinek AC jest przekątną kwadratu ABCD. Oblicz pole i obwód tego kwadratu gdy

Zad. 48 (6p) Dane są wierzchołki trójkąta
Wyznacz współrzędne punktu B i równania prostych zawierających boki trójkąta ABC, jeśli wiadomo, że sin kąta
.

Zad. 49 (7p) Kąt ostry rombu ma miarę 30
, pole jest równe 8, wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków rombu jeśli wiadomo, że bok AB jest równoległy do osi OX, a romb zawarty jest w I ćwiartce układu współrzędnych.

Zad. 50 (5p) Dane są proste o równaniach

a)Wyznacz liczbę a, tak aby proste były prostopadłe

b)Wyznacz liczbę a, tak aby proste przecinały oś OY w tym samym punkcie.

Zad. 51 (4p) Oblicz pole równoległoboku ABCD jeśli
.

Odpowiedzi

Funkcja liniowa - poziom podstawowy

1. f(x)=
x-1

2. f(x)=-2x+4, f(
)=3-
.

3. y
y
y

4. y=x+5

5. a)m
) b)m=

c)m=1.

6. x
16,2).

10. (
.

11. f(x)=x+2 lub f(x)=x+3.

12. a) f(x)=
, b)y=

13. a) y=0,068x,x
, x-droga w km, y- ilość paliwa b) 808,8km.

14. a)500zł , b)y=1.22x,x
,x-cena bez VAT-u, y- cena z VAT-em.

15. Jan ma 3600zł,a Zofia 2400zł.

16. Koców grubych 52 sztuki, a cienkich 23 sztuki.

17. ZW=
.

18. a) x-y-5=0 A(0,1) C(7
b)y
.

19. v=80km/h, s=480km.

20. f(x)=-x+6, g(x)=2x, x
,f(x)
.

21. a)540 b)17000zł.

22. C(0,8).

23. 35 osób, 875zł.

24. P(-1;-
), R(3; -
).

25. y=
, y=
.

26.
v
, punkt spełnia nierówność.

27. CD:
, AD:

28. AC:
, BC:
, AB:
, B
, C

29.
,

30..

31.

32. Nie można wpisać okręgu,

33.
więc

34.
proste nie są prostopadłe.

36. Kąt jest ostry.

37.
.

39.
,
.

40.

41.

42.

43.

44.

45. k=0

46. d=5

47. P=36, Obw.=24

48.

49.

50. a)
b)

51. P=40

---