PRZYGOTOWANIE DO SPRAWDZIANU -

FUNKCJA LINIOWA - POZIOM ROZSZERZONY

DOPUSZCZAJĄCY

1. Motocyklista jadący ze stałą prędkością w ciągu 4 sekund przejeżdża 32 metry.

Ile km przejedzie kolarz w ciągu 1,5 godziny, jadąc z tą samą prędkością.

2. Sprawdź algebraicznie, czy do wykresu funkcji liniowej
należy punkt :

a)
b)

3. Punkt
należy do wykresu funkcji liniowej
. Wyznacz b.

4. Na podstawie wykresu funkcji liniowej f :

1. wyznacz współczynnik kierunkowy tej funkcji

2. określ monotoniczność funkcji

3. Podaj współrzędne punktu przecięcia wykresu z osią OX

5. a) Oblicz miejsce zerowe funkcji liniowej
.

b) Dla jakich argumentów funkcja liniowa
przyjmuje wartości dodatnie ?

6. Napisz wzór oraz naszkicuj wykres funkcji liniowej :

1. do której wykresu należą punkty
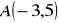
   i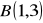
   

2. wiedząc, że miejscem zerowym jest liczba 3 oraz
   

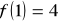
7. Wyznacz kąt nachylenia wykresu funkcji liniowej
do osi OX.

8. Wyznacz m, dla którego wykresy funkcji liniowych
oraz
są :

a) równoległe b) prostopadłe

9. Napisz wzór funkcji liniowej, której wykres jest :

1. równoległy do wykresu funkcji
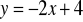
   i przechodzi przez punkt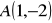
   ;

2. prostopadły do wykresu funkcji
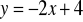
   i przechodzi przez punkt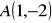
   .

10. W korporacji taksówkowej obowiązuje następujący system opłaty za przejazd : za pierwszy

kilometr 6,30 zł, a za każdy następny (rozpoczęty) kilometr 1,80 zł. Podaj wzór funkcji f

opisującej wysokość opłaty za przejazd w zależności od liczby n przejechanych kilometrów.

11. Rozwiąż równanie i nierówność : a)

b)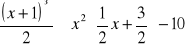

12. Rozwiąż układ równań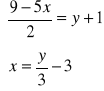
metodą podstawiania lub przeciwnych współczynników.

13. Podaj interpretację graficzną nierówności
w układzie współrzędnych.

14. Suma dwóch liczb jest równa 35. Jeżeli jedną z nich potroić, a drugą pomnożyć przez 4

to otrzymamy w sumie 125. Znajdź te liczby.

DOSTATECZNY

1. Wyznacz wzór funkcji liniowej
, wiedząc, że jej wykres przecina oś OY

w punkcie
oraz
.

2. Napisz wzór funkcji liniowej wiedząc, że :

1. jej wykres przechodzi przez punkt
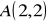
   i jest nachylony do osi OX pod kątem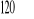
   .

b)
i
oraz narysuj wykres tej funkcji.

3. Dla jakich wartości parametru m, funkcja liniowa
ma

nieskończenie wiele miejsc zerowych.

4. Wyznacz wartości parametru k, dla których prosta określona równaniem

przechodzi przez I, II i III ćwiartkę układu współrzędnych.

5. Dana jest funkcja liniowa f o wzorze
.

a) Dla jakich a funkcja f jest malejąca ?

b) Dla
wyznacz zbiór tych argumentów, dla których wartości funkcji f należą do przedziału

.

6. Napisz wzór funkcji liniowej, której wykres otrzymujemy w wyniku przesunięcia równoległego

wykresu funkcji
o wektor
.

7. Dla jakich wartości parametru k, wykres funkcji liniowej
przecina oś OY

poniżej punktu
.

8. Dane są wzory funkcji liniowych : f(x) = 2x - 4, g(x) = x + 1, h(x) = ax - 7

Dla jakich a wykresy funkcji przecinają się w tym samym punkcie ?

9. Naszkicuj wykres funkcji f(x) =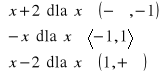
.

a) Oblicz wartość funkcji f dla argumentu 6.

b) Oblicz miejsca zerowe funkcji f

10. a) Rozwiąż równanie
.

b) Rozwiąż nierówność
. Wypisz wszystkie liczby naturalne spełniające

tę nierówność.

11. Dane jest równanie z niewiadomą x. Przedyskutuj liczbę i rodzaj rozwiązań równania

ze względu na wartość parametru m.

12. Dopisz brakujące równanie układu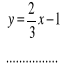
tak, aby powstały układ równań był :

a) sprzeczny b) nieoznaczony c) oznaczony

13. Dany jest układ równań z niewiadomymi x i y :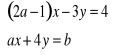
.

a) Rozwiąż ten układ dla
i
metodą wyznacznikową.

b) Dobierz współczynniki a i b tak, aby rozwiązaniem układu równań była para liczb
.

14. Rozwiąż układ równań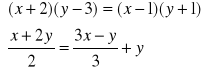
.

15. Podaj interpretację graficzną układu nierówności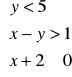
w układzie współrzędnych.

16. Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają równanie

17. Pan Nowak ma sklep z owocami i warzywami. W hurtowni kupił 80 kg jabłek oraz 20 kg

papryki czerwonej za łączną kwotę 328 zł. Do ceny hurtowej jabłek sklepikarz doliczył

20% marży, zaś do ceny hurtowej papryki doliczył 25% marży. Wówczas za 5 kg jabłek i 2 kg

papryki trzeba było zapłacić w sklepie pana Nowaka 29 zł. Ile kosztuje 1 kg jabłek oraz 1 kg

papryki czerwonej w hurcie, a ile w detalu ?

DOBRY

1. Wyznacz te wartości parametru m :

1. dla którego miejsce zerowe funkcji
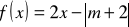
   jest liczbą nie mniejszą niż 4.

2. dla których wykresy funkcji f i g są równoległe, gdy
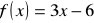
   oraz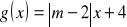
   .

3. dla których funkcji f i g są prostopadłe, gdy
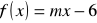
   oraz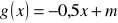
   .

4. dla których funkcja f dana wzorem
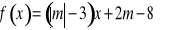
   jest rosnąca i jednocześnie

wykres funkcji f przecina oś OY poniżej punktu
.

2. Napisz wzór funkcji liniowej f, której wykres przechodzi przez punkt A(-
, -2) i jest nachylony

do osi OX pod takim kątem α, że cos α =
. Podaj wzór proporcjonalności prostej, której

wykres jest prostopadły do wykresu funkcji f.

3. Dane są dwie funkcje liniowe
oraz
. Wyznacz wartość parametru m,

dla którego zbiorem rozwiązań nierówności
jest przedział
.

4. Dane są dwie funkcje liniowe
oraz
. Wyznacz wartość

parametru m, dla którego zbiór rozwiązań nierówności
zawiera się

w przedziale
.

5. Rozwiąż układ nierówności :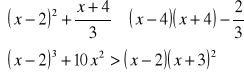

6. Rozwiąż równanie : a)
metodą algebraiczną

b)
metodą graficzną.

7. Rozwiąż nierówność : a)
metodą algebraiczną

b)
metodą graficzną.

8. Dane jest równanie z niewiadomą x. Przedyskutuj liczbę i rodzaj rozwiązań równania

ze względu na wartość parametru k.

9. W zależności od wartości parametru a przeprowadź dyskusję istnienia i liczby rozwiązań

układu równań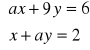
.

10. Dla jakich wartości parametru m rozwiązaniem układu równań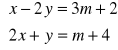
jest para

liczb ujemnych ?

11. Opisz za pomocą układu nierówności :

1. trójkąt o wierzchołkach
   ,
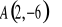
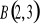
   i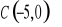
   .

2. przedstawioną figurę geometryczną

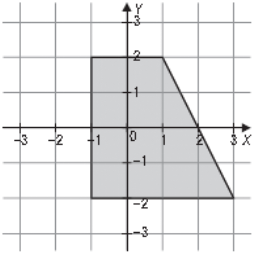
12. Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają równanie :

a)
b)

13. Oblicz, ile lat ma obecnie syn, ile lat ma jego ojciec, a ile dziadek, jeżeli wiadomo, że połowa

wieku ojca równa się
sumy lat dziadka i syna, że 5 lat temu ojciec miał o 35 lat mniej

niż dziadek i syn razem oraz że za 3 lata dziadek będzie miał o 7 lat więcej niż ojciec

i syn razem.

14. Suma cyfr pewnej liczby trzycyfrowej wynosi 18. Cyfra dziesiątek jest o 1 większa od cyfry

jedności. Jeśli zamienimy miejscami cyfrę setek i dziesiątek, to otrzymamy liczbę o 180 większą

od początkowej. Wyznacz liczbę początkową.

BARDZO DOBRY

1. Wyznacz wartość parametru m, dla której dziedziną funkcji
jest R.

2. Wyznacz wzór funkcji liniowej, która dla każdego
spełnia warunek
.

3. Narysuj wykres funkcji :
. Zbadaj liczbę rozwiązań równania f(x) = k,

k∈R, ze względu na wartość parametru k.

4. Naszkicuj wykres funkcji f(x) =
· x + 3, a następnie określ liczbę rozwiązań równania

f(|x|) = p w zależności od wartości parametru p (p
R).

5. Dana jest funkcja
, gdzie
.

a) Wyznacz wartości parametru k, dla których równanie
ma dwa rozwiązania ujemne.

b) Dla jakich wartości parametru a rozwiązania równania
są liczbami o różnych

znakach ?

6. Rozwiąż równanie
.

7. Rozwiąż nierówność
.

8. Przedyskutuj liczbę rozwiązań równania
w zależności od wartości

parametrów p i k. W przypadku istnienia rozwiązania, wyznacz je i przedstaw w najprostszej

postaci.

9. Dla jakich wartości parametru k rozwiązanie układu równań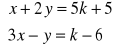

spełnia warunek
?

10. Rozwiąż układ równań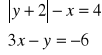
.

11. Wyznacz wartości parametru m, dla których punkt wspólny prostych określonych równaniami :

oraz
należy do kwadratu ABCD, gdzie
,
,

,
.

12. Zilustruj w układzie współrzędnych zbiór punktów, których współrzędne spełniają równanie

.

13. Miejscowości A, B oraz C lezą przy tej samej drodze, przy czym miejscowość B leży pomiędzy

A i C. Z miejscowości A i B, odległych o 36 km, wyruszają jednocześnie dwaj rowerzyści.

Każdy z nich jedzie ze stałą prędkością. Gdyby obaj jechali naprzeciw siebie, to spotkaliby się

po
godz. Gdyby jechali w kierunku miejscowości C, to po 5 godzinach jazdy odległość

między nimi wynosiłaby 24 km. Z jaką prędkością jedzie każdy rowerzysta ?

---