Jurasz Witold
KBI gr. 2
PROJEKT nr 1
1.Określenie parametrów geotechnicznych podłoża:
Zgodnie zPN-86/B-024480:
Pg- piasek gliniasty
Pd-piasek drobny
Gπ-glina pylasta
Ps-piasek średni
1.1).Wartości normowe:
Zgodnie z PN-81/B-03020 wartości parametrów geotechnicznych dla poszczególnych
rodzajów gruntów wynoszą:
Pg Pd Gπ Ps
γ(n) zg. z tabl.2 dla zg. z tabl.1 dla zg. z tabl.2 dla zg. z tabl.1
(ciężar objętościowy) ρ=2,15tmˉ³ ρ=1,9tmˉ³ ρ=2,00tmˉ³ ρ=2,00tmˉ³
γ=21,09kN/m³ γ=18,64kN/m³ γ=19,62kN/m³ γ=19,62kN/m³
Ø(n) zg. z rys.4 zg. z rys.3 zg.z rys.4 zg. z rys.3
(kąt tarcia wewnętrznego) dla gr. C dla gr.C
Ø=15º Ø=30º Ø=12º Ø=32º
C(n)
(spójność) 17[kPa] !!!!!!!!! 12[kPa] !!!!!!!!!
M0 zg. z rys.7 zg. z rys.6 zg. z rys7 zg. z rys.6
(moduł ściśliwości gruntu 30000[kPa] 52000[kPa] 20000[kPa] 95000[kPa]
pierwotnej)
M
(moduł ściśliwości gruntu zg. z tabl.3 zg. z tabl.3 zg. z tabl.3 zg. z tabl.3
wtórnej) dla β=0,60 dla β=0,80 dla β=0,60 dla β=0,90
zg. ze wzorem 50000[kPa] 65000[kPa] 33333,3[kPa] 105555,6[kPa]
β=M0/M
1.2).Wartości obliczeniowe:
--dla Pg : γ(r) =21,09 x 0,9=18,98[kN/m³] ; Ø(r)=13,5º ; c(r)=15,3[kPa] ;
--dla Pd : γ(r)= 16,78[kN/m³] ; Ø(r)= 27º ; c(r)= ----------- ;
--dla GΠ: γ(r)= 17,66[kN/m³] ; Ø(r)= 10,8º ; c(r)= 10,8[kPa} ;
--dla Ps: γ(r)= 17,66[kN/m³] ; Ø(r)= 28,8º ; c(r)= ----------- ;
2.Określenie poziomu posadowienia:
poz. Posadowienia - 1,50 [m] w Pg, o IL=0,18
3.Wstępne przyjęcie wymiarów fundamentu:
qf = (1+0,3·B/L)·Nc·c(r)+(1+1,5·B/L)·ND·γD(r)·Dmin+(1-0,25·B/L)·NB·γB·B
Przyjmując L=B (stopa fundamentowa o podstawie kwadratowej), oraz posadowienie jej w gruncie spoistym ( w którym zakładamy dość małe kąty tarcia):
qfprzybliż. = 1,3·Nc·c(r)+2,5·ND·γD(r)·Dmin
wg.PN - 81/B-03020 zg. z rys. 21-1:
dla Pg - Ø(r) = 13,5º
NC=10
ND=3,5
Dmin=1,5[m]
qfprzybl.= 1,3·10·15,3+2,5·3,5·18,98·1,5 = 448[kN/m²]
Obliczenie powierzchni podstawy fundamentu:
F = N/(qfprzybl - 22·D)
γgr. przybl = 22[kN/m³] , D = 1,5[m] , N = 1080[kN]
F = 1080/(448-22·1,5) = 26020[cm²]
F=B x L
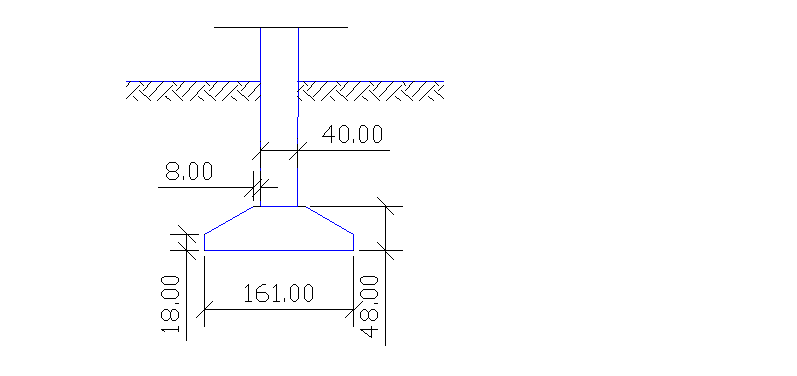
B=161[cm] L=161[cm]
aS - wymiar równoległy słupa
hfekon = α·(L-aS) = 0,4·(161-40) = 48[cm]
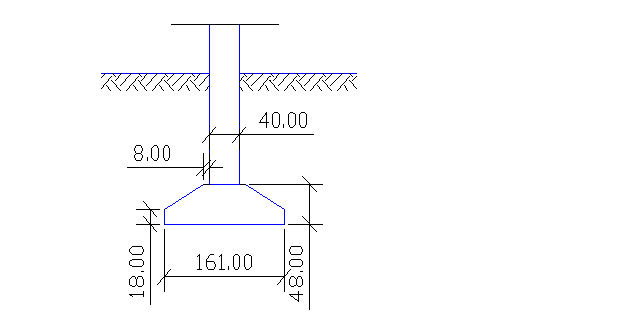
Przyjęcie wymiarów stopy fundamentowej:
4.Obliczenie obciążeń w poziomie posadowienia:
Dla obciążeń pionowych:
Gs - ciężar słupa
Gf - ciężar fundamentu
Gz - ciężar gr. na odsadzkach fund.
γb - ciężar objętościowy betonu - 24[kN/m³]
Vs - objętość słupa
Vf - objętość fundamentu
Vz - objętość gruntu zalegającego nad fundamentem
γz(r) - wartość obliczeniowa ciężaru objętościowego gr. nad stopą fund.
Gs=Vs·γb·1,1
Vs=0,4·0,4·(1,5-0,48)=0,1632[m³]
Gs=0,1632·24·1,1=4,308[kN]
Gf=Vf·γb·1,1
Vf=F·0,18+1/3·0,3·(F+A+√(F·A))
A=(0,08+0,4+0,08)²=0,3136[m²]
Vf=2,602·0,18+1/3·0,3·(2,602+0,3136+√(0,3136·2,602))=0,85025[m³]
Gf=0,85025·24·1,1=22,4466[kN]
Gz=Vz·γz(r)
Vz=1,5·(1,61)²-Vs-Vf=2,876[m³]
Gz=2,876·18,98=54,59[kN]
Nrc=N+Gs+Gf+Gz=1080+4,308+22,4466+54,59=1161,34[kN]Dla momentu: eB=ΣM/ΣN=(M+Hr·D)/Nrc=(6,8+6,8·1,5)/1161,34~1,5[c
m]
Wartość zredukowana szerokości stopy fundamentowej: B=B-2·eB=1,61-2·1,5=1,58[m]
5.Sprawdzenie warunków obliczeniowych:
5.1.Pierwszy stan graniczny:
Qr ≤ m·Qf
Nr ≤ m·QfNB
≤ m·QfNL
QfNB= B·L·[(1+0,3·B/L)·NC·c(r)·iC+(1+1,5·B/L)·ND·γD·Dmin·iD+(1-0,25·B/L)·NB·γB(r)·B·iB]
Gdzie: L=L
NB=0,44
tgδL=Hr/Nr=6,8/1136,7=0,005982
tgδL/tgØ(r)=0,0249 - to zgodnie z Z1-2:
ic,iD,iB=1
γD(r)=18,98[kN/m³]
γB(r):
γ'=(γS-γW)·(1-n)
n= (γS -γd)/ γS
γd=γ/(1+wn)
zg z PN dla Pd o Id=0,40 -- γ=19[kN/m³] , wn=0,24
γd=19/(1+0,24)=15,32[kN/m³]
n=(26,5-15,32)/26,5½0,422
γ'=(26,5-10)·(1-0.422)=9,537[kN/m³]
γB=(18,98·1,3+9,537·0,4)/1,7=16,76[kN/m³]
QfNB=1,61·1,58·[(1+0,3·1,58/1,61)·10·15,3·+(1+1,5·1,58/1,61)·3,5·1,5·18,98·1+
+(1-0,25·1,58/1,61)·0,44·16,76·1,58·1] = 1152,76
Ponieważ warunek Nr ≤ m·QfNB , gdzie m=0.81 nie został spełniony, przewymiarowuję
fundament.
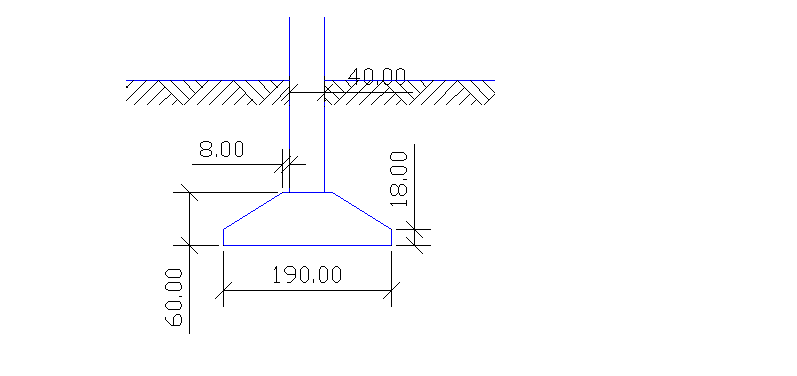
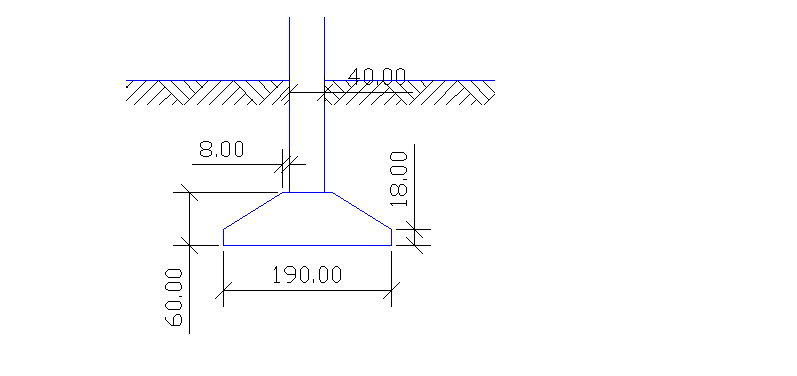
Przyjmuję następujące wymiary stopy fund: B=L=1,9[m]
hfekon=0,4·(1,9-0,4)=0,60[m]
4.Obliczenie obciążeń w poziomie posadowienia:
Vs=0,4·0,4·(1,5-0,60)=0,144[m³]
Gs= Vs·γb·1,1=0,144·24·1,1=3,8016[kN]
F=(1,9)²=3,61[m²]
Vf=F·0,18+1/3·0,42·(3,61+0,3136+√(3,61·0,3136))=1,348064[m³]
Gf=Vf·γb·1,1=1,34864·24·1,1=35,5889[kN]
Vz=1,5·F-Vf-Vs=1,5·3,61-1,34806-0,144=3,92294[m³]
Gz=Vz·γz(r)=3,92294·18,98=74,4574[kN]
Nrc=N+Gs+Gf+Gz=1080+3,8016+35,5889+74,4574=1193,8479[kN]
Dla momentu: eB=(M+Hr·D)/Nr+(6,8+6,8·1,5)/1193,8479=1,42[cm]
B=B-2· eB=1,7-2·1,42=1,872[m]
L=L
5.Sprawdzenie warunków obliczeniowych :
5.1.Pierwszy stan graniczny:
Nr ≤ m·QfNB
QfNB= 1,872·1,9·[(1+0,3·1,872/1,9)·10·15,3·1+(1+1,5·1,872/1,9)·3,5·18,98·1,5·1+
+(1-0,25·1,872/1,9)·0,44·16,76·1,872·1]=1620,26[kN]
Nr=1193,8479 ≤ m·QfNB=0,81·1620,26=1312,41
5.2. Uwzględnienie wpływu warstwy słabej:
Ponieważ na głębokości h≤2B od poziomu posadowienia pojawia się warstwa słabsza niż ta, w której fundament został posadowiony rozpatruję warunek pierwszego stanu granicznego z uwzględnieniem tej właśnie warstwy.
Nr' = Nr+B'·L'·h·γ(r)
B=B'-2·eB' L=L'-2·eL'
D'min= Dmin+h=1,5+2,2=3,7[m]
B'=B+b
Dla gruntów spoistych i h=2,2>B=1.9 :
b=h/3=2,2/3=0,73[m]
B'=1,9+0,73=2,63[m]
L'=L+b=1,9+0,73=2,63[m]
Nr'= Nr+B'·L'·h·γ(r)
γ(r)=( γ(r)(Pg)·h1+γ'(Pd)·h2)/( h1+ h2)=(18,98·1,3+9,537·0,9)/2,2=15,12[kN/m³]
Nr'=1193,8479+2,63·2,63·2,2·15,12=1423,93[kN]
tgδB=Hr/Nr'=6,8/1423,93=0,0048
dlatego przyjmuję wsp.iC=1 , iD=1 , iB=1
Dla warstwy słabej:
Ø(r)=10,8º , c(r)=10,8 , γB=γ'=10,03[kN/m³]
γD=(9,537·0,9+18,98·2,8)/3,7=16,68[kN/m³]
eB'=(Nr· eB+Hr·h)/Nr'=(1193,8479·0,0142+6,8·2,2)/1423,93=0,0224[m]
dla Ø(r)=10,8º => Nc=8,39 , ND=2,59 , NB=0,24
B=2,63-2·0,0224=2,58[m]
L=L'=2,63[m]
Q'fNB= B·L·[(1+0,3·B/L)·NC·c(r)·iC+(1+1,5·B/L)·ND·γD·D'min·iD+(1-0,25·B/L)·NB·γB(r)·B·iB]
Q'fNB=2,58·2,63·[(1+0,3·2,58/2,63)·8,39·10,8·1+(1+1,5·2,58/2,63)·2,59·16,68·3,7·1+
+(1-0,25·2,58/2,63)·0,24·10,03·2,58·1]=3508,18
Nr'=1423,93<m· Q'fNB=0,81·3508,18=2841,63
Warunek został spełniony.
5.3. Drugi stan graniczny:
Układ Warstw |
z [m] |
h [m] |
σzγ [kPa] |
z B |
η |
σzs [kPa] |
σzd [kPa] |
M [kPa] |
M0 [kPa] |
S'' [cm] |
S' [cm] |
S [cm] |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
p.p.- 1.5 [m] Pg -Il=0,18 γ=21,09 |
0 |
1,5 |
31,635 |
|
|
31,635 |
243,95 |
|
|
|
|
|
Pg - Il=0,18 γ=21,09 |
0,3 |
0,6 |
44,289 |
0,16 |
0,85 |
26,89 |
207,36 |
50000 |
30000 |
0,032 |
0,41 |
0,442 |
Pg - Il=0,18 γ=21,09 |
0,95 |
0,7 |
59,052 |
0,5 |
0,5 |
15,82 |
121,98 |
50000 |
30000 |
0,022 |
0,285 |
0,307 |
Pd - ID=0,40 γ'= 9,537 |
1,75
|
0,9 |
67,635 |
0,92 |
0,3 |
9,4905 |
73,185 |
65000 |
52000 |
0,0131
|
0,1267
|
0,1398
|
Gπ - Il=0,36 γ'= 10,03 |
2,50
|
0,6 |
73,653 |
1,32 |
0,14 |
6,011 |
46,351 |
33333,3 |
20000 |
0,0108 |
0,1390 |
0,1498
|
Gπ - Il=0,36 γ'= 10,03 |
3,10 |
0,6 |
79,671 |
1,63 |
0,15 |
4,7453 |
36,593 |
33333,3 |
20000 |
0,0085 |
0,1098
|
0,1183
|
Ps - ID=0,48 γ'= 10,197 |
3,85 |
0,9 |
88,85 |
2,03 |
0,1 |
3,164 |
24,395 |
105555,6 |
95000 |
0,0027 |
0,0231
|
0,0258
|
Σsi = 0,7533 [cm]
Obliczenia do tabeli:
Dla h=1,5 - Pg Il=0,18
σzγ=1,5·21,09=31,635[kPa]
σzd=q- σzs
q=Nr/L·B·1,2=1193,8479/1,9·1,9·1,2=275,59[kPa]
σzd=275,59-31,635=243,95[kPa]
Dla h=0,6 - Pg Il=0,18
σzγ=0,6·21,09+31,635=44,289[kPa]
ηS=0,85
σzs=q· ηS=31,635·0,85=26,89[kPa]
σzd=243,95·0,85=297,36[kPa]
s''= σzs·h/M=26,89·0,6/50000=0,032[cm]
s'= σzd·h/M0=207,36·0,6/30000=0,41[cm]
Dla h=0,7 - Pg Il=0,18
σzγ=0,7·21,09+44,289=59,052[kPa]
ηS=0,5
σzs=0,5·31,635=15,82[kPa]
σzd=0,5·243,95=121,975[kPa]
s''=15,82·0,7/50000=0,022[cm]
s'=121,975·0,7/30000=0,285[cm]
Dla h=0,9 - Pd Id=0,40
γ'=9,537[kN/m³]
σzγ=0,9·9,537+59,052=67,635[kPa]
ηS=0,3
σzs=0,3·31,635=9,4905[kPa]
σzd=0,3·243,95=73,185[kPa]
s''=9,4905·0,9/65000=0,01314[cm]
s'=73,185·0,9/52000=0,1267[cm]
Dla Gп - IL=0,36 h=0,6[m]
γ'=10,03[kN/m³]
σzγ=0,6·10,03+67,635=73,653[kPa]
ηS=0,19
σzs=0,19·31,635=6,011[kPa]
σzd=0,19·243,95=46,351[kPa]
s''=6,011·0,6/33333,3=0,0108[cm]
s'=46,351·0,6/20000=0,1390[cm]
Dla Gп - IL=0,36 h=0,6[m]
γ'=10,03[kN/m³]
σzγ=0,6·10,03+73,653=79,671[kPa]
ηS=0,15
σzs=0,15·31,635=4,74525[kPa]
σzd=0,15·243,95=36,5925[kPa]
s''=4,74525·0,6/33333,3=0,0085[cm]
s'=36,5925·0,6/20000=0,1098[cm]
Dla h=0,9 - Ps ID=0,40
γ=20[kN/m³]
wN=0,22
γs=26,5[kN/m³]
γd= γ/(1+ wN)=20/(1+0,22)=16,39[kN/m³]
n= (γs- γd)/ γs=(26,5-16,39)/26,5=0,382
γ'=( γs- γw)·(1-n)=(26,5-10)·(1-0,382)=10,197[kN/m³]
σzγ=0,9·10,197+79,671=88,85[kPa]
ηS=0,1
σzs=0,1·31,635=3,164[kPa]
σzd=0,1·243,95=24,395[kPa]
s''=3,164·0,9/105555,6=0,0027[cm]
s'=24,395·0,9/95000=0,0231[cm]
Osiadanie średnie budowli:
Sśr=Σ Sj·Fj/Σ Fj
-S1=1,18[cm] F1=(1,9m)²
-S2=1,24[cm] F2=(2,5m)²
-S3=1,06[cm] F3=(2,0m)²
-S4=1,28[cm] F4=(1,9m)²
-S5=1,36[cm] F5=(2,5m)²
-S6=1,20[cm] F6=(2,0m)²
-S7=1,20[cm] F7=(1,9)²
-S8=1,24[cm] F8=(2,5m)²
-S9=1,00[cm] F9=(2,0m)²
Sśr=[1,18·(1,9)²+1,24·(2,5)²+1,06·2²+1,28·(1,9)²+1,36·(2,5)²+1,2·2²+1,2·(1,9)²+1,24·(2,5)²+1·2²]/
[(1,9)²+(2,5)²+2²+(1,9)²+(2,5)²+2²+(1,9)²+(2,5)²+2²]=50,2526/41,58=1,208[cm]
Sśr=1,208[cm] < Sśrdop=7[cm]
Warunek na osiadanie średnie budowli został spełniony.
2.Przechylenie budowli Θ:
S=ax+by+c
a,b,c - niewiadome wsp. Równania
x,y - bieżące współrzędne poziome
aΣxj²+bΣ xjyj+cΣxj=Σxjsj
aΣxjyj+bΣyj²+cΣyj=Σyjsj
aΣ xj+bΣyj+nc=Σsj
Σxj²=(-9)²+0²+9²+(-9)²+0²+9²(-9)²+0²+9²=486
Σxjyj=-9·6+0·6+9·6+(-9)·0+0+9·0+(-9)·(-6)+0·(-6)+9·(-6)=0
Σyj²=6²+6²+6²+0²(-6)²+(-6)²+(-6)²=216
Σ xj=-9+0+9-9+0+9-9+0+9=0
Σyj=6+6+6+0-6-6-6=0
Σxjsj=-9·0,018+0+9·0,0106-9·0,0128+0+9·0,012-9·0,012+0+9·0,01=-0,0918
Σyjsj=6·0,018+6·0,012+6·0,0106+0-6·0,012-6·0,0124-6·0,01=0,0396
Σsj=0,018+0,0124+0,0106+0,0128+0,0136+0,012+0,012+0,0124+0,01=0,1138
486a+0b+0c=-0,0918 a=0,00018889
0a+216b+0c+0,0396 => b=0,0001833
0a+0b+9c=0,1138 c=0,01264
Θ=(a²+b²)=[(0,00018889)²-(0,0001833)²]1/2=0,000263
Θ=0,000263 < Θdop=0,003
Warunek został spełniony.
3.Strzałka ugięcia budowli f0:
f0=1/l·(l·s0-l1·s2-l2·s1)
Rozpatruję przypadek dla stóp 1- 5 - 9:
s1=1,18[cm] , s5=1,36[cm] , s9=1,00[cm]
l2= l1=(6²+9²)1/2=10,817[m]=1081,7[cm]
l=2163,3[cm]
f0=1/2163,3·(2163,3·1,36-1081,7·1-1081,7·1,18)=0,2699[cm]
f0=0,2699[cm] , f0dop=1[cm]
Warunek został spełniony.
Wnioski końcowe:
Ponieważ zarówno 1-szy jak i 2-gi stan graniczny dla przyjętej stopy fundamentowej jest spełniony ostateczne wymiary są następujące:
10
Wyszukiwarka
Podobne podstrony:
Mechanizm wrzodotwórczej reakcji stresowej gr 5b wtorek
Sprawozdanie Gr, Poniedziałek - Materiały wiążące i betony, 07. (17.11.2011) Ćw I - Badanie właściwo
Mechanizm wrzodotwórczej reakcji stresowej gr 5b wtorek
13 ZACHOWANIA ZDROWOTNE gr wtorek 17;00
Mat termoizol gr 10 ponoc zzzz wnioskami, Poniedziałek - Materiały wiążące i betony, 07. (17.11.201
Kolokwium 1 (zbiorcze opracowane), GRUPA PONIEDZIAŁKOWA: (gr
Temat 9 gr wtorek 17 30 alkohol i narkotyki
13 ZACHOWANIA ZDROWOTNE gr wtorek 17;00
PRI gr 414 11 30 wtorek
Mechanika gr proj 2
Mechanika gr proj TG
Mechanika gr proj TG
mapy do celow proj
26 poniedziałek
Aksjologia (gr
Budżet i podatki gr A2
SEM odcinek szyjny kregoslupa gr 13 pdg 1
więcej podobnych podstron