Wojskowa Akademia Techniczna
im. Jarosława Dąbrowskiego

Laboratorium Fizyki Ogólnej

Sprawozdanie z ćwiczenia laboratoryjnego

Nr 28

Tytuł: Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej.

Wykonał: Paweł Wojno gr. C04H Warszawa dnia: 31.12.2004r

Prowadzący zajęcia: mgr inż. Piotr Marciniak

Ocena przygotowania do zajęć:……….……………………..

Ocena końcowa:………………………………

I. Opis teoretyczny

Zjawisko rozchodzenia się fal o rozmaitych kształtach powierzchni falowych ,jak również zjawiska: ugięcia (dyfrakcji), odbicia i załamania można opisywać za pomocą zasady Huyghensa (czyt. Hojhensa), według której każdy punkt ośrodka, do którego dociera czoło fali, staje się samodzielnym źródłem wysyłającym elementarne fale kuliste. W następnej fazie ruchu fali, fale wytworzone w ten sposób nakładają się. Zasadę ta Mozy również zastosować dla fal płaskich Zjawisko to nazywamy dyfrakcją albo ugięciem fali.

Podobne zjawisko nastąpi, gdy zamiast dużej przegrody z otworkiem ustawić na drodze fali małą przeszkodę. Wtedy fala ugina się na brzegach przeszkody. Możemy takie zjawisko zaobserwować, gdy źródło dźwięku jest odgrodzone od obserwatora jakąś przeszkodą. Fale świetlne, jak wiemy, polegają na rozchodzeniu się zmiennych pól: elektrycznego i pola magnetycznego, które opisywane są przez wektor elektryczny i wektor magnetyczny. Wrażenie świetlne, jak stwierdzono, wywołuje wektor elektryczny, dlatego nazywany jest wektorem świetlnym. W zjawisku interferencji światła, polegającym na nakładaniu się fal świetlnych, wektory świetlne fal składowych dodają się. Przekonuje nas o tym doświadczenie wykonane przez Younga, który to ustawił ekran zaopatrzony w mały otworek prostopadle do promieni światła Słonecznego. Zgodnie z zasadą Huygensa otworek ten działa jako źródło rozchodzących się elementarnych fal kulistych, które padając na otworki umieszczone w drugim ekranie ponownie generują dwie fale kuliste. Na trzecim ekranie Young otrzymał szereg rozłożonych na przemian jasnych i ciemnych prążków.

Warunkiem wystąpienia interferencji światła było wystąpienie zjawiska dyfrakcji światła. Takie następstwo jest charakterystyczne dla doświadczeń interferencyjnych, także dla wykonywanego przez nas doświadczeniu z siatką dyfrakcyjną.

Rozważmy obecnie, jakie muszą być spełnione warunki, aby w danym punkcie ekranu wystąpiło maksimum, względnie minimum natężenia światła. Wiemy, że przy superpozycji dwóch drgań równoległych o jednakowych częstotliwościach amplitudy drgań dodają się, gdy fazy są zgodne, jednak odejmują się, gdy fazy są przeciwne. Zatem, gdy fazy fal docierających do rozważanego punktu (rys. 1.1) będą zgodne, to w punkcie tym wystąpi maksimum. Fazy fal będą zaś zgodne, jeżeli w różnicy dróg optycznych
zawierać się będzie wielokrotność długości fali, wiec:

,
(1.1)

Jeżeli w omawiany punkcie fazy fal będą przeciwne, to wystąpi minimum, co nastąpi wówczas, jeżeli odcinek
będzie zawierał nieparzystą wielokrotność połówek długości fali.

Na podstawie przeprowadzonych wyżej rozważań możemy stwierdzić, że fale o jednakowych długościach wzmacniają się najsilniej, jeżeli różnica ich dróg optycznych ∆L jest równa wielokrotności długości fali, a maksymalnie się osłabiają, jeżeli różnica ich dróg optycznych jest nieparzystą wielokrotnością połówek długości fali.

Rys. 1.1 ilustracja warunku wzmocnienia interferencyjnego

Liczbę k nazywamy rzędem obrazu interferencyjnego i stanowi ona numer porządkowy kolejnych obrazów. Jeżeli bowiem będziemy wstawiać do równania (1.1) wartości k=0, 1, 2, ...to fizycznie będzie to odpowiadać różnicom dróg równym odpowiednio 0,
, 2
,..., a więc obrazom interferencyjnym powstałym pod coraz większymi kątami
:

Prążek zerowy (nieugięty)

Prążek pierwszego rzędu

Prążek pierwszego rzędu

Prążek pierwszego rzędu

Siatką dyfrakcyjną nazywamy zbiór dużej liczby jednakowych, równoległych szczelin, między którymi występują równe odstępy. Rys. 1.1 pokazuje fragment siatki składający się z dwóch szczelin o szerokości a. Odległość d między ich środkami nazywamy s t a ł ą siatki dyfrakcyjnej. Należy zauważyć, że zależność (1.1) jakkolwiek wyprowadzona dla układu dwóch szczelin słuszne są również dla siatki dyfrakcyjnej.

Jeśli równanie (28.1) przekształcimy do postaci:

Widzimy, że kąt pod jakim ugięte jest k-te widmo interferencyjne zależy od długości fali oraz od stałej siatki d. Jeżeli użyte w doświadczeniu światło będzie niemonochromatyczne, np. białe, to wszystkie prążki interferencyjne prócz zerowego (nieugiętego) będą sobą przedstawiały widmo użytego światła.

II. Opis układu pomiarowego

Rys. 1.2 Schemat układu pomiarowego

Źródłem światła Z dającym widmo liniowe (lampa rtęciowa lub sodowa) oświetlamy wąską (~1mm) prostokątną szczelinę w ekranie E. Wiązka promieni po przejściu przez szczelinę w ekranie pada na siatkę dyfrakcyjną. Promienie przez nią ugięte wchodzą do umieszczonego za siatką oka ludzkiego. Na przedłużeniu wiązek ugiętych wchodzących do oka, obserwator ujrzy na tle ekranu pozorne widmo źródła światła utworzone przez siatkę dyfrakcyjną (szereg prążków barwnych z prawej i lewej strony szczeliny).

III. Wykonywane czynności, pomiary

Pierwszym wykonywanym przez nas pomiarem jest pomiar odległości(L) siatki dyfrakcyjnej od ekranu. Wykonujemy piec pomiarów tej odległości.

W doświadczeniu wykonujemy pomiary dla widma czerwonego i zielonego. Wykonujemy po 5 pomiarów odległości h dla każdego z 4 prążków danego koloru. Według tego wykonujemy po piec pomiarów prążka czerwonego pierwszego rzędu z lewej i z prawej, i po pięć pomiarów prążka drugiego rzędu po lewej po prawej stronie. Analogicznie wykonujemy pomiary prążka zielonego.

Poniższe tabela przedstawiają rezultaty wykonywanych pomiarów:

Pomiary odległości L
pomiar	odległość L
1	75,60
2	75,50
3	75,70
4	75,45
5	75,50

Pomiary dla widma czerwonego
rząd	prawa strona	lewa strona
1	1[cm]	[cm]
		8,95	9,05
		8,90	9,10
		9,00	9,00
		8,80	8,95
		9,00	8,95
	2	[cm]	[cm]
		18,25	18,40
		18,30	18,40
		18,15	18,35
		18,40	18,30
		18,30	18,30

Pomiary dla widma zielonego
rząd	prawa strona	lewa strona
1	[cm]	[cm]
		7,85	7,80
		7,90	7,95
		8,00	7,90
		7,90	7,90
		7,80	7,95
	2	[cm]	[cm]
		16,00	16,00
		16,10	16,05
		16,10	16,10
		16,15	16,20
		15,90	16,10

IV. Obliczenia

Wyznaczam wartości średnie h_s jako średnie arytmetyczne dziesięciu pomiarów położeń prążków oddzielnie dla pierwszego i drugiego rzędu widma.

Obliczam długości poszczególnych fal na podstawie mierzonych linii widma.

Korzystam z następującej zależności:

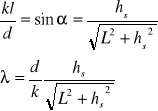
wyliczamy ze wzoru ,gdzie stała siatki dyfrakcyjnej d wynosi 5,2

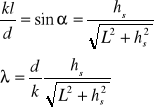
Żólta 1:

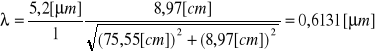
Żólta 2:

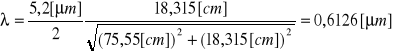
Fioletowa 1:

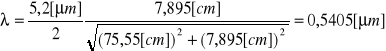
Fioletowa 2:

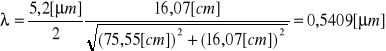
Błąd :

(zakładamy ze stała siatki d nie jest obarczona błędem)

Do obliczenia odchylenia standardowego wykorzystujemy wzór:

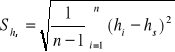
obliczamy błąd względny korzystając ze wzoru:

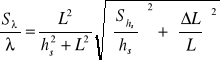
Żólta 1 :

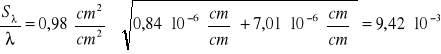
Żólta 2 :

Fioletowa 1 :

Fioletowa 2 :

następnie wyliczamy wartość średnia tych błędów dla widma każdej barwy:

fioletowa

żólta

V. Tabela z wynikami

	k
zolty	1	8,95	9,05	8,97	0,0823	75,55	0,2	0,6131	0,6128	0,0058	0,0043
												8,90	9,10
												9,00	9,00
												8,80	8,95
												9,00	8,95
			2									18,25	18,40	18,315	0,0784			0,6126		0,0029
												18,30	18,40
												18,15	18,35
												18,40	18,30
												18,30	18,30
		fioletowy	1									7,85	7,80	7,895	0,0643	75,55	0,2	0,5405	0,5407	0,0046	0,0038
												7,90	7,95
												8,00	7,90
												7,90	7,90
												7,80	7,95
			2									16,00	16,00	16,07	0,0856			0,5409		0,0031
												16,10	16,05
												16,10	16,10
												16,15	16,20
												15,90	16,10

VI. Wnioski

W naszym doświadczeniu uzyskaliśmy następujące wyniki naszych obliczeń:

Wyniku uzyskane w naszym doświadczeniu są dość dokładne i wiarygodne(maja sens fizyczny). Największy wpływ na dokładność pomiarów miał pomiar odległości sitki dyfrakcyjnej od ekrany i pomiar odległości h poszczególnych prążków. Można zmniejszyć te nie dokładności przez zastosowanie bardziej precyzyjnego urządzenia do pomiarów tych odległości. Niestety nie znamy rzeczywistych wartości mierzonych fal i nie możemy stwierdzić czy mieszczą się one w granicy wyznaczonego błędu.

---