1. Dane

Przedmiotem analizy niezawodnościowej jest belka żelbetowa, prostokątna poddana zginaniu. Zostanie przeanalizowany stan graniczny nośności.

;

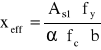
 = 0,85

f_c - wytrzymałość betonu na ściskanie

f_y - granica plastyczności stali

A_s1 - pole przekroju zbrojenia podłużnego

b - szerokość belki

d -użyteczna wysokość przekroju betonowego

_{eff, lim} - maksymalna wysokość względna strefy ściskanej przekroju betonowego

Przeanalizowano dwa równania projektowe:

Do obliczeń przyjęto element o następujących charakterystykach:

Zmienna	Wartość założona	lX	VX	mX	sX
fy	350	1,14	0,04	399	15,96
fc	25	1,25	0,16	31,25	5
b	35	1,01	0,04	35,35	1,414
d	56	0,99	0,04	55,44	2,2176
As	19,64	1	0,015	19,64	0,2946

Analizę przeprowadzono dla 100 losowych danych ( w tabeli podane pierwsze 30 danych):

i	b	d	As	fy	fc
1	0,902913328	0,418712167	0,121227438	0,662789592	0,772650264
2	0,482076753	0,672600039	0,38352118	0,785992666	0,018348551
3	0,687114492	0,816308538	0,772833273	0,445303993	0,412445508
4	0,3627518	0,177475306	0,206902373	0,541846093	0,838661259
5	0,796753594	0,196309312	0,19953145	0,681804289	0,703554557
6	0,128376345	0,165084472	0,809700869	0,211250167	0,820635892
7	0,995412562	0,505923585	0,283559845	0,899215901	0,676424048
8	0,158103184	0,886859321	0,052564805	0,41068666	0,371898941
9	0,942692876	0,05671588	0,450279653	0,565010881	0,630830628
10	0,398066291	0,217981465	0,407795995	0,183185228	0,598929139
11	0,62037499	0,007299429	0,175797141	0,273451834	0,294401644
12	0,914106538	0,899017479	0,715052071	0,781790888	0,529874601
13	0,651641068	0,461986906	0,737711863	0,179636992	0,109778834
14	0,978252363	0,384731688	0,279537402	0,42622888	0,349254251
15	0,627788204	0,661234114	0,548156604	0,205156144	0,237330482
16	0,719282052	0,191561434	0,657338583	0,049814706	0,033985976
17	0,28035959	0,536172274	0,933548977	0,441557523	0,987595906
18	0,622863222	0,959231586	0,595825512	0,747756736	0,390723389
19	0,351032263	0,824732292	0,813682567	0,930232825	0,505730575
20	0,699182763	0,907167262	0,387822136	0,02789991	0,991305222
21	0,885244836	0,501005125	0,012525224	0,216342947	0,819914499
22	0,200856768	0,58265835	0,221553175	0,915407437	0,591618934
23	0,825648263	0,498985988	0,085062201	0,427762326	0,50087574
24	0,647436335	0,752713185	0,607205837	0,265132649	0,311971096
25	0,683575838	0,607519687	0,579856575	0,079074778	0,079462577
26	0,60963465	0,662177659	0,982745777	0,804718864	0,613296829
27	0,433226325	0,458120903	0,757605115	0,355290123	0,399485244
28	0,927069693	0,416713655	0,65116369	0,515629539	0,555911414
29	0,962779467	0,756132318	0,289929301	0,209034209	0,817328395
30	0,668477221	0,186817729	0,606994846	0,136289924	0,193495438
…	…	…	…	…	…

2. Rozkład normalny poszczególnych zmiennych

rozład normalny		bi=μb+zi*σb	rozład normalny		di=μd+zi*σd
szerokość belki b			wysokość użyteczna belki d
ui	zi	bi	ui	zi	di
0,902913328	1,298332176	37,1858417	0,418712167	-0,20518923	54,98497236
0,482076753	-0,04494188	35,28645218	0,672600039	0,44710413	56,43149812
0,687114492	0,487687771	36,03959051	0,816308538	0,901386248	57,43891414
0,3627518	-0,35111313	34,85352603	0,177475306	-0,92502931	53,388655
0,796753594	0,830081112	36,52373469	0,196309312	-0,85487794	53,54422268
0,128376345	-1,13410003	33,74638256	0,165084472	-0,97377362	53,28055961
0,995412562	2,60547094	39,03413591	0,505923585	0,014848693	55,47292846
0,158103184	-1,0022842	33,93277015	0,886859321	1,209993901	58,12328247
0,942692876	1,577788363	37,58099274	0,05671588	-1,58295486	51,9296393
0,398066291	-0,25835561	34,98468517	0,217981465	-0,77902826	53,71242693
0,62037499	0,306465966	35,78334288	0,007299429	-2,44218031	50,02422095
0,914106538	1,366484932	37,28220969	0,899017479	1,275973432	58,26959868
0,651641068	0,38975494	35,90111349	0,461986906	-0,09542919	55,22837623
0,978252363	2,018921186	38,20475456	0,384731688	-0,29307706	54,7900723
0,627788204	0,326001181	35,81096567	0,661234114	0,415833702	56,36215282
0,719282052	0,580709902	36,1711238	0,191561434	-0,87215659	53,50590554
0,28035959	-0,58177348	34,5273723	0,536172274	0,09079488	55,64134673
0,622863222	0,313009526	35,79259547	0,959231586	1,741837339	59,30269848
0,351032263	-0,3825352	34,80909522	0,824732292	0,933551182	57,5102431
0,699182763	0,522051449	36,08818075	0,907167262	1,323511453	58,375019
0,885244836	1,201621505	37,04909281	0,501005125	0,002519462	55,44558716
0,200856768	-0,83856467	34,16426956	0,58265835	0,208698973	55,90281084
0,825648263	0,937107015	36,67506932	0,498985988	-0,00254174	55,43436344
0,647436335	0,378408408	35,88506949	0,752713185	0,683052333	56,95473685
0,683575838	0,47772168	36,02549846	0,607519687	0,27286043	56,04509529
0,60963465	0,278367094	35,74361107	0,662177659	0,418413788	56,36787442
0,433226325	-0,16816604	35,11221322	0,458120903	-0,10516874	55,2067778
0,927069693	1,454309438	37,40639355	0,416713655	-0,21030805	54,97362086
0,962779467	1,783892308	37,87242372	0,756132318	0,693915007	56,97882592
0,668477221	0,43571227	35,96609715	0,186817729	-0,8896841	53,46703654
…	…	…	…	…	…

rozład normalny		Asi=μAs+zi*σAs	rozład normalny		fyi=μfy+zi*σfy
pole powierzchni prętów zbrojeniowych As			granica plastycznosci stali fy
ui	zi	Asi	ui	zi	fyi
0,121227438	-1,1688731	19,29564998	0,662789592	0,42008858	405,7046137
0,38352118	-0,29624599	19,55272593	0,785992666	0,792593324	411,6497895
0,772833273	0,748209835	19,86042262	0,445303993	-0,13753485	396,8049438
0,206902373	-0,81721623	19,3992481	0,541846093	0,105085551	400,6771654
0,19953145	-0,84329584	19,39156504	0,681804289	0,472750204	406,5450933
0,809700869	0,876794354	19,89830362	0,211250167	-0,80209076	386,1986315
0,283559845	-0,57229849	19,47140087	0,899215901	1,27709682	419,3824652
0,052564805	-1,62047804	19,16260717	0,41068666	-0,22577909	395,3965657
0,450279653	-0,12495473	19,60318834	0,565010881	0,163686109	401,6124303
0,407795995	-0,23321829	19,57129389	0,183185228	-0,90329279	384,583447
0,175797141	-0,93150127	19,36557972	0,273451834	-0,60240621	389,3855969
0,715052071	0,568204761	19,80739312	0,781790888	0,778255571	411,4209589
0,737711863	0,636306911	19,82745602	0,179636992	-0,91674927	384,3686816
0,279537402	-0,58421615	19,46788992	0,42622888	-0,18598345	396,0317041
0,548156604	0,121005248	19,67564815	0,205156144	-0,82334399	385,8594299
0,657338583	0,405210553	19,75937503	0,049814706	-1,64665273	372,7194224
0,933548977	1,502755933	20,0827119	0,441557523	-0,14702145	396,6535376
0,595825512	0,242556635	19,71145718	0,747756736	0,667446976	409,6524537
0,813682567	0,891548586	19,90265021	0,930232825	1,477527535	422,5813395
0,387822136	-0,28499999	19,556039	0,02789991	-1,91259472	368,4749882
0,012525224	-2,24062262	18,97991258	0,216342947	-0,78460358	386,4777268
0,221553175	-0,76695799	19,41405418	0,915407437	1,374827232	420,9422426
0,085062201	-1,37180456	19,23586638	0,427762326	-0,18207402	396,0940986
0,607205837	0,272043976	19,72014416	0,265132649	-0,6276009	388,9834897
0,579856575	0,201526636	19,69936975	0,079074778	-1,4113228	376,4752882
0,982745777	2,114078437	20,26280751	0,804718864	0,858597952	412,7032233
0,757605115	0,698619399	19,84581328	0,355290123	-0,37107706	393,0776101
0,65116369	0,38846423	19,75444156	0,515629539	0,039187319	399,6254296
0,289929301	-0,55359117	19,47691204	0,209034209	-0,80977667	386,0759643
0,606994846	0,271495203	19,71998249	0,136289924	-1,09714098	381,48963
...	…	…	…	…	…

rozład normalny		fci=μfc+zi*σfc
wytrzym. betonu na ściskanie fc
ui	zi	fci
0,772650264	0,747603061	34,9880153
0,018348551	-2,08911658	20,80441711
0,412445508	-0,22125878	30,14370609
0,838661259	0,988970698	36,19485349
0,703554557	0,5346514	33,923257
0,820635892	0,917791049	35,83895525
0,676424048	0,45772243	33,53861215
0,371898941	-0,3268283	29,6158585
0,630830628	0,334054259	32,9202713
0,598929139	0,250576416	32,50288208
0,294401644	-0,54057095	28,54714523
0,529874601	0,074954471	31,62477235
0,109778834	-1,2277055	25,11147248
0,349254251	-0,38733475	29,31332625
0,237330482	-0,71491574	27,67542131
0,033985976	-1,82519195	22,12404023
0,987595906	2,244375244	42,47187622
0,390723389	-0,27743429	29,86282856
0,505730575	0,014364838	31,32182419
0,991305222	2,378365508	43,14182754
0,819914499	0,915039187	35,82519593
0,591618934	0,231711567	32,40855784
0,50087574	0,002195144	31,26097572
0,311971096	-0,49027093	28,79864534
0,079462577	-1,40869608	24,20651959
0,613296829	0,287922301	32,68961151
0,399485244	-0,25467985	29,97660075
0,555911414	0,140611041	31,9530552
0,817328395	0,905230526	35,77615263
0,193495438	-0,86508713	26,92456436
…	…	…

3. Obliczenie nośności Rn dla wartości dokładnych

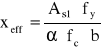
→ x_eff = 9,24 cm < x_eff,lim = 30,8 cm

→ Rn = 35318,6 kNcm = 353,19 kNm

4. Obliczenie nośności Rn dla zmiennych losowych

i	bi	di	Asi	fyi	fci	xeff	Rn
1	37,1858	54,985	19,2956	405,7046	34,988	7,0787	402,7335
2	35,2865	56,4315	19,5527	411,6498	20,8044	12,8989	402,2993
3	36,0396	57,4389	19,8604	396,8049	30,1437	8,53434	419,0313
4	34,8535	53,3887	19,3992	400,6772	36,1949	7,24882	386,8093
5	36,5237	53,5442	19,3916	406,5451	33,9233	7,48566	392,6116
6	33,7464	53,2806	19,8983	386,1986	35,839	7,47524	380,7225
7	39,0341	55,4729	19,4714	419,3825	33,5386	7,33836	423,0276
8	33,9328	58,1233	19,1626	395,3966	29,6159	8,87003	406,7868
9	37,581	51,9296	19,6032	401,6124	32,9203	7,48658	379,3656
10	34,9847	53,7124	19,5713	384,5834	32,5029	7,78738	374,9755
11	35,7833	50,0242	19,3656	389,3856	28,5471	8,68456	344,4728
12	37,2822	58,2696	19,8074	411,421	31,6248	8,13141	441,7171
13	35,9011	55,2284	19,8275	384,3687	25,1115	9,94526	383,0017
14	38,2048	54,7901	19,4679	396,0317	29,3133	8,0993	391,2037
15	35,811	56,3622	19,6756	385,8594	27,6754	9,01216	393,6931
16	36,1711	53,5059	19,7594	372,7194	22,124	10,827	354,1861
17	34,5274	55,6413	20,0827	396,6535	42,4719	6,39072	417,7784
18	35,7926	59,3027	19,7115	409,6525	29,8628	8,88774	442,9766
19	34,8091	57,5102	19,9027	422,5813	31,3218	9,07533	445,5253
20	36,0882	58,375	19,556	368,475	43,1418	5,44511	401,0267
21	37,0491	55,4456	18,9799	386,4777	35,8252	6,5018	382,8644
22	34,1643	55,9028	19,4141	420,9422	32,4086	8,68336	421,3676
23	36,6751	55,4344	19,2359	396,0941	31,261	7,8184	392,5812
24	35,8851	56,9547	19,7201	388,9835	28,7986	8,73246	403,3965
25	36,0255	56,0451	19,6994	376,4753	24,2065	10,0052	378,5476
26	35,7436	56,3679	20,2628	412,7032	32,6896	8,41997	436,1717
27	35,1122	55,2068	19,8458	393,0776	29,9766	8,71942	396,6552
28	37,4064	54,9736	19,7544	399,6254	31,9531	7,77035	403,3115
29	37,8724	56,9788	19,4769	386,076	35,7762	6,52916	403,9079
30	35,9661	53,467	19,72	381,4896	26,9246	9,13962	367,8523
…	…	...	…	…	…	…	…

i	Pi	Ri sort	zi
1	0,009901	339,533	-2,33008
2	0,019802	344,473	-2,05785
3	0,029703	354,089	-1,88518
4	0,039604	354,186	-1,7553
5	0,049505	355,772	-1,64967
6	0,059406	358,571	-1,55978
7	0,069307	358,758	-1,48097
8	0,079208	360,212	-1,41042
9	0,089109	367,852	-1,34626
10	0,09901	371,767	-1,28721
11	0,108911	374,947	-1,23234
12	0,118812	374,975	-1,18095
13	0,128713	375,327	-1,1325
14	0,138614	377,161	-1,08657
15	0,148515	378,201	-1,04282
16	0,158416	378,548	-1,00099
17	0,168317	379,366	-0,96084
18	0,178218	380,532	-0,92218
19	0,188119	380,723	-0,88485
20	0,19802	382,617	-0,84872
21	0,207921	382,864	-0,81366
22	0,217822	383,002	-0,77957
23	0,227723	385,248	-0,74637
24	0,237624	385,856	-0,71397
25	0,247525	386,381	-0,6823
26	0,257426	386,809	-0,6513
27	0,267327	387,034	-0,62092
28	0,277228	387,372	-0,5911
29	0,287129	387,966	-0,56179
30	0,29703	389,565	-0,53296
31	0,306931	390,403	-0,50457




























5. Parametry statystyczne nośności

Rn	mRn	sRn	lRn	VRn
353,19	400,41	24,46	1,13	0,06

Kombinacje wartości średnich obciążeń




σ²_Qmax = σ²_D + σ²_{L max}

Obliczenie μ_R




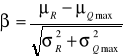
σ_X = V_X ·μ_{X →} σ_R = V_R·μ_R




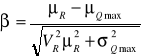
β = 4,0 → μ_R

Przykład:

zmienna	Xn	λx	Vx	λxmax	Vxmax	λxave	Vxave	μ	σ	μmax	σmax	μave	σave
Dn	20	1,05	0,1					21	2,1
Ln	80			1	0,18	0,24	0,65			80	14,4	19,2	12,48







Proporcje obciążeń							równ. 1	równ. 2	przyjęte φ		Nośności		μR nowe		σ^2Rmax nowe		beta
Dn	Ln	Dn/(Dn+Ln)	μRmax	σ^2Rmax	μR	Rn	φ 1	φ 2	φ 1	φ 2	R1	R2	μR1	μR2	σ^2R1max	σ^2R2max	β1	β2
0	100	0	100	324	184,53	162,769	1,04443	0,86012	1	0,95	170	147,37	192,73	167,07	11,771038	10,203995	5,57033	5,95244
10	90	0,1	100,5	263,54	178,26	157,238	1,06208	0,89037	1	0,95	167	147,37	189,33	167,07	11,563313	10,203995	5,43185	5,75983
20	80	0,2	101	211,77	172,42	152,087	1,07833	0,92053	1	0,95	164	147,37	185,93	167,07	11,355589	10,203995	5,28829	5,56283
30	70	0,3	101,5	168,68	167,13	147,421	1,09211	0,94966	1	0,95	161	147,37	182,52	167,07	11,147865	10,203995	5,13938	5,36134
40	60	0,4	102	134,28	162,59	143,416	1,10169	0,97618	1	0,95	158	147,37	179,12	167,07	10,940141	10,203995	4,98482	5,15525
50	50	0,5	102,5	108,56	159,01	140,258	1,1051	0,99816	1	0,95	155	147,37	175,72	167,07	10,732417	10,203995	4,82428	4,94447
60	40	0,6	103	91,53	156,65	138,177	1,10004	1,0132	1	0,95	152	147,37	172,32	167,07	10,524692	10,203995	4,6574	4,72889
70	30	0,7	103,5	83,18	155,73	137,365	1,0847	1,01918	1	0,95	149	147,37	168,92	167,07	10,316968	10,203995	4,4838	4,50842
80	20	0,8	104	83,52	156,39	137,947	1,05838	1,01488	1	0,95	146	147,37	165,52	167,07	10,109244	10,203995	4,30307	4,28295
90	10	0,9	104,5	92,54	158,63	139,923	1,02199	1,00055	1	0,95	143	147,37	162,12	167,07	9,9015199	10,203995	4,11475	4,05239
100	0	1	105	100,25	160,58	141,643	0,9884	0,9884	1	0,95	140	147,37	158,72	167,07	9,6937957	10,203995	3,91836	3,81664

Po przeprowadzeniu w analogiczny sposób pozostałych kombinacji otrzymano:










1




---