Łukasz Łużyński 15.V.2002

Ćwiczenie 5a

Temat: Badanie ruchu obrotowego bryły sztywnej i wyznaczenie momentu bezwładności przyrządu (wahadło Oberbecka).

1. PODSTAWY TEORETYCZNE

1) Pierwsza zasada dynamiki ruchu obrotowego

W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem jednostajnym, gdy nie działają na nią żadne momenty sił lub, gdy momenty działające równoważą się wzajemnie.

Warunek równowagi bryły w ruchu obrotowym:

2) Druga zasada dynamiki ruchu obrotowego

Jeżeli na bryłę obracającą się wokół osi OZ kartezjańskiego układu współrzędnych działa niezrównoważony moment siły M, wtedy nadaje on tej bryle przyspieszenie kątowe ε, którego wartość jest proporcjonalna do wartości momentu siły, a zwrot i kierunek są identyczne ze zwrotem i kierunkiem tego momentu siły.

Moment bezwładności bryły złożonej z kilku części jest równy sumie momentów bezwładności poszczególnych części bryły względem tej samej osi obrotu. Moment bezwładności zależy od wyboru osi, względem której go obliczamy. Jeżeli jest to oś 0-0 przechodząca przez środek masy S, to moment bezwładności I₀ jest parametrem charakteryzującym daną bryłę. Moment bezwładności I_d względem dowolnej osi d-d równoległej do osi 0-0 można obliczyć z twierdzenia Steinera:

gdzie:

m - masa bryły

r - odległość obydwu osi

II. OPIS PRZEPROWADZONEGO DOŚWIADCZENIA

Celem doświadczenia było wyznaczenie momentu bezwładności dla dwóch różnych konfiguracji wahadła Oberbecka przedstawionych na poniższych rysunkach. W doświadczeniu tym dokonywaliśmy pomiaru czasu spadania odważnika, przyczepionego do nici nawiniętej na walcu stanowiącego oś obrotu wahadła Oberbecka. Otrzymane pomiary umieszczone zostały w tabeli i wykorzystane do obliczeń zgodnie ze wzorem roboczym.

III. WYPROWADZENIE WZORU ROBOCZEGO

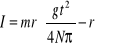
IV. OBLICZENIA I WYZNACZANIE NIEPEWNOŚCI POMIARÓW

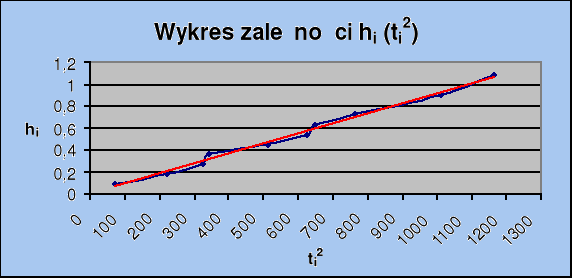
1) Zależność h(t²)

1. Położenie skrajne

Lp.	N	t [s]		t^2
1	24	34,1	1,078195	1162,81	0,000927	0,001854
2	20	31,8	0,898495	1011,24	0,000889	0,001777
3	16	27,66	0,718796	765,0756	0,00094	0,001879
4	14	25,46	0,628947	648,2116	0,00097	0,001941
5	12	24,97	0,539097	623,5009	0,000865	0,001729
6	10	22,59	0,449248	510,3081	0,00088	0,001761
7	8	18,56	0,359398	344,4736	0,001043	0,002087
8	6	18,03	0,269549	325,0809	0,000829	0,001658
9	4	14,87	0,179699	221,1169	0,000813	0,001625
10	2	8,47	0,08985	71,7409	0,001252	0,002505

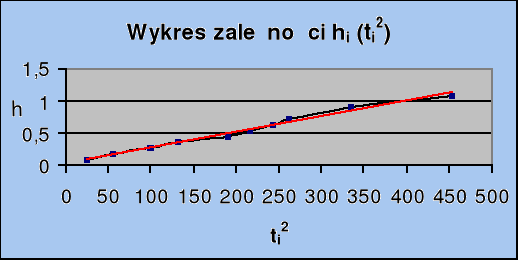
b) Położenie środkowe

Lp.	N	t [s]		t^2
1	24	21,31	1,078195	454,1161	0,002374	0,004749
2	20	18,28	0,898495	334,1584	0,002689	0,005378
3	16	16,19	0,718796	262,1161	0,002742	0,005485
4	14	15,62	0,628947	243,9844	0,002578	0,005156
5	12	14,71	0,539097	216,3841	0,002491	0,004983
6	10	13,78	0,449248	189,8884	0,002366	0,004732
7	8	11,5	0,359398	132,25	0,002718	0,005435
8	6	10	0,269549	100	0,002695	0,005391
9	4	7,47	0,179699	55,8009	0,00322	0,006441
10	2	4,97	0,08985	24,7009	0,003638	0,007275

2) Wyznaczanie momentu bezwładności

Masa ciężarka

Przyspieszenie ziemskie

Promień walca

Liczba nawiniętych zwojów

1. Skrajne położenie

ti [s]
24	0,122	0,014884
24,56	-0,438	0,191844
23,9	0,222	0,049284
24,54	-0,418	0,174724
24,6	-0,478	0,228484
24,15	-0,028	0,000784
24,03	0,092	0,008464
23,91	0,212	0,044944
23,78	0,342	0,116964
23,75	0,372	0,138384

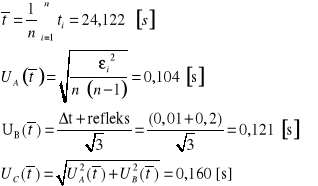
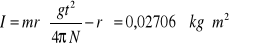
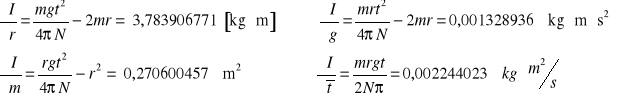
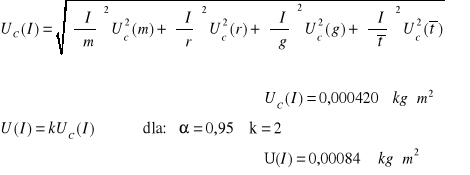
2. Środkowe położenie

ti [s]
14,41	-0,15	0,0225
13,59	0,67	0,4489
13,78	0,48	0,2304
13,59	0,67	0,4489
14,66	-0,4	0,16
14,56	-0,3	0,09
14,71	-0,45	0,2025
14,15	0,11	0,0121
14,62	-0,36	0,1296
14,53	-0,27	0,0729

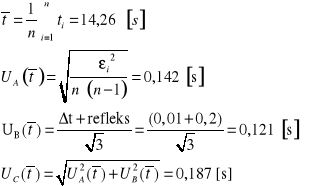
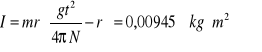
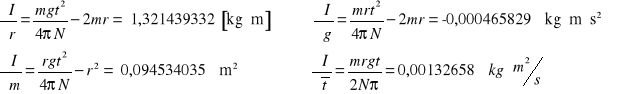
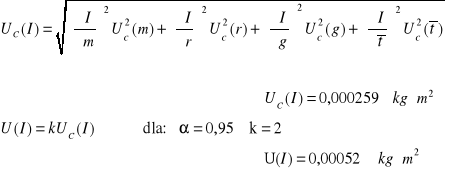
V. WNIOSKI

• wykresy zależności h(t²) są wykresami funkcji liniowo rosnących, jest to dowodem tego, że odważnik porusza się ruchem jednostajnie przyspieszonym,

• Dokonywaliśmy pomiarów momentów bezwładności dla dwóch różnych konfiguracji, w pierwszym przypadku odważniki wahadła były położone w skrajnej odległości od środka osi obrotu, w drugim przypadku odważniki znajdowały się o połowę bliżej środka wahadła. Moment bezwładności w pierwszym przypadku jest znacznie większy od przypadku drugiego, można tu nawiązać do przykładu łyżwiarza, który by zwiększyć swoją prędkość obrotową zmniejsza swój moment bezwładności poprzez złożenie ramion wzdłuż ciała.

---