Nr.ćw 104	Data: 14.03 96	Sebastian Rabcewicz	Wydział Elektryczny	Semestr II	Grupa 9 - ( E7 )
					Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat :Wyznaczanie prędkości dźwięku w powietrzu metodą przesunięcia fazowego

1. Rozchodzenie się dźwięku odbywa się w postaci fali mechanicznej i może mieć miejsce tylko w ośrodku sprężystym .Falą nazywamy proces rozchodzenia się drgań w ośrodku .

Można wyróżnić fale poprzeczne ( gdy kierunek drgań cząsteczek jest zgodny z kierunkiem fali) oraz fale podłużne ( kierunek drgań jest prostopadły do kierunku fali ). Charakter fali zależy od własności sprężystych ośrodka w którym się rozchodzi .

Najczęściej spotykanym ruchem drgającym jest ruch harmoniczny , w którym wychylenie y zmienia się w czasie zgodnie ze wzorem :

,

A - jest amplitudą ,

- częstością kołową ,

0 - fazą początkową .

Faza początkowa określa stan ruchu w chwili t=0 . Kolejne punkty ośrodka pobudzane są do drgań i osiągają tę samą fazę z pewnym opóźnieniem . Prędkością fali jest prędkość przesuwania się wychylenia o stałej fazie .

Wychylenie y dowolnej cząstki w chwili t , w odległości x od źródła drgań opisane jest funkcją falową :

gdzie : - częstość kołowa ,

k = 2/ - liczba falowa ,

- długość fali ,

0 - faza w punkcie x = 0 i w chwili t = 0 .

Równanie to jest podwójnie okresowe : względem czasu i przestrzeni . Długością fali jest odległość pomiędzy najbliższymi punktami posiadającymi tę samą fazę .

Związek pomiędzy prędkością a długością fali :

Prędkość fali w powietrzu .

Prędkość rozchodzenia się fal podłużnych w ośrodku ciągłym :

E - jest modułem Younga ośrodka , jego gęstością .

Przekształcając prawo Hooke'a można napisać :

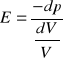
dp i dV są różniczkowymi zmianami ciśnienia i objętości gazu o objętości V.

Drgania dźwiękowe rozchodzą się tak szybko , że ściskanie i rozrzedzanie gazu można uznać za przemiany adiabatyczne , wobec czego zmiana stanu gazu zachodzi zgodnie ze wzorem Poissona :

ℵ- stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości .

Różniczkując wzór Poissona otrzymujemy :

Stosując równanie stanu gazu we wzorze na gęstość otrzymujemy :

gdzie n - ilość moli gazu

R - stała gazowa ,

T - temperatura .

Ilość moli n można wyrazić jako stosunek całej masy gazu do masy 1 mola : n=m/.

Uwzględniając to w powyższych równaniach otrzymujemy wzór na prędkość dźwięku :

2. Tabela pomiarów.

częstotliwość	odczyt	dł. fali	śr.dł.fali	prędkość	różniczka log.	śr.prędkość	UWAGI
[Hz] +/- 1	[m] +/- 0.001	[m]	[m]	[m/s]	[m/s]	[m/s]
2205	0.604
	0.281	0.646					błąd
	0.605	0.648	0.646667	1425.9			gruby
	0.282	0.646
4001	0.799
	0.703	0.096
	0.614	0.089
	0.477	0.137					bł. gruby
	0.377	0.100
	0.278	0.099	0.096375	385.5964	4.097375
	0.377	0.099
	0.478	0.101
	0.613	0.135					bł. gruby
	0.702	0.089
	0.800	0.098
6002	0.863
	0.804	0.059
	0.740	0.064
	0.679	0.061
	0.616	0.063
	0.557	0.059	0.0611	366.7222	6.0631
	0.616	0.059
	0.678	0.062
	0.741	0.063
	0.804	0.063
	0.862	0.058
8016	0.865
	0.817	0.048
	0.777	0.040
	0.729	0.048
	0.686	0.043
	0.640	0.046	0.0451	361.5216	8.0611
	0.687	0.047
	0.728	0.041
	0.777	0.049
	0.817	0.040
	0.866	0.049
częstotliwość	odczyt	dł. fali	śr.dł.fali	prędkość	różniczka log.	śr.prędkość	UWAGI
[Hz]	[m]	[m]	[m]	[m/s]	[m/s]	[m/s]
10020	0.853
	0.816	0.037
	0.780	0.036
	0.748	0.032
	0.711	0.037
	0.678	0.033	0.035	350.7	10.055
	0.711	0.033
	0.748	0.037
	0.781	0.033
	0.817	0.036
	0.853	0.036
12012	0.842
	0.815	0.027
	0.784	0.031
	0.756	0.028
	0.726	0.030
	0.695	0.031	0.0294	353.1528	12.0414
	0.726	0.031
	0.756	0.030
	0.785	0.029
	0.815	0.030
	0.842	0.027
14045	0.838
	0.812	0.026
	0.788	0.024
	0.763	0.025
	0.738	0.025
	0.711	0.027	0.0254	356.743	14.0704
	0.738	0.027
	0.764	0.026
	0.788	0.024
	0.813	0.025
	0.838	0.025

częstotliwość	odczyt	dł. fali	śr.dł.fali	prędkość	różniczka log.	śr.prędkość	UWAGI
[Hz]	[m]	[m]	[m]	[m/s]	[m/s]	[m/s]
16016	0.835
	0.813	0.022
	0.791	0.022
	0.769	0.022
	0.747	0.022
	0.726	0.021	0.0219	350.7504	16.0379
	0.748	0.022
	0.770	0.022
	0.791	0.021
	0.813	0.022
	0.836	0.023
						360.7409107

Uwagi:

1. Wartość długości fali w tabeli obliczałem odejmując dwie sąsiednie odległości .

2. Prędkość dźwięku w tabeli obliczałem mnożąc średnią długość fali przez daną częstotliwość f.

3. Błąd wartości złożonej obliczyłem za pomocą różniczki logarytmicznej

4. Obliczenie wartości odchylenia standardowego średniej.

- odchylenie standardowe średniej obliczam ze wzoru

- - odchylenie wartości poszczególnego pomiaru od wartości średniej

V	Vśr
385.5964		24.85546	617.7941
366.7222		5.981289	35.77582
361.5216		0.780689	0.609476
350.7	360.7409	-10.0409	100.8199	928.3723	5.56289
353.1528		-7.58811	57.57942
356.743		-3.99791	15.98329
350.7504		-9.99051	99.8103

Ponieważ odchylenie standardowe wartości średniej obliczałem dla siedmiu pomiarów, otrzymałem zaniżoną wartość tego odchylenia. Aby otrzymać wartość odchylenia standardowego średniej odpowiadającą dużej serii pomiarów mnożę przez tzw. współczynnik Studenta - Fishera t_n

- dla siedmiu pomiarów współczynnik ten wynosi 1.1

3. Obliczam prędkość dźwięku na podstawie równania

- do obliczeń przyjmuję :

Otrzymuje ( jest to prędkość dźwięku dla temperatury 20^o C )

4. WNIOSKI

Wyznaczona doświadczalnie średnia prędkość dźwięku w powietrzu wynosi 360.74 m/s i jest porównywalna z wartością otrzymaną ze wzoru 342.84 m/s

W czasie doświadczenia w kilku przypadkach otrzymane wartości dość znacznie różniły się od pozostałych i dlatego zostały odrzucone jako tzw. błędy grube. Przyczyną ich powstania mogły być błędy odczytu lub specyficzne właściwości zestawu pomiarowego.

Ze względu na małą liczbę pomiarów ( < 10 ) wartość odchylenia standardowego średniej arytmetycznej została pomnożona przez tzw. współczynnik Studenta - Fishera.

Innymi źródłami błędów mogła być niedokładność odczytu odległości mikrofonu od głośnika, oraz przede wszystkim niedokładność odczytu z oscyloskopu.

Prędkość we wzorze została obliczona dla temperatury 20^o C . Temperatura w laboratorium mogła się różnić od założonej co miało również wpływ na wynik końcowy.

---