Statystyka

Wykład trzeci

Związek pomiędzy wiekiem żony i męża małżeństw zawartych w roku 1933:

Wiek żony (w latach)	Wiek Męża (w latach)													Razem
		15 - 20	20 - 25	25-30	30 - 35	35 - 40	40 - 45	45 - 50	50 - 55	55 - 60	60 - 65	65 - 70	70 - 75		75 i więcej
15-20	33	189	56	8	2	-	-	-	-	-	-	-	-	288
20-25	18	682	585	106	19	5	2	1	-	-	-	-	-	1418
25-30	1	140	511	179	40	14	6	3	1	1	-	-	-	896
30-35	-	11	75	101	42	20	10	5	2	1	1	-	-	268
35-40	-	2	75	24	28	19	13	8	5	2	1	-	-	112
40-45	-	-	10	5	9	14	12	10	6	4	2	1	-	64
45-50	-	-	1	1	3	5	9	9	7	4	3	1	-	42
50-55	-	-	-	-	-	1	3	7	6	5	3	1	-	26
55-60	-	-	-	-	-	-	1	3	5	4	3	1	-	17
60-65	-	-	-	-	-	-	-	1	1	4	3	2	-	11
65-70	-	-	-	-	-	-	-	-	1	1	3	2	1	8
70 i więcej	-	-	-	-	-	-	-	-	-	-	1	1	1	3
RAZEM	52	1024	1238	424	78	78	56	47	34	26	20	9	2	3153

Związek korelacyjny - taki związek cech, w którym odmianom cechy niezależnej towarzyszą różne co do swojej wartości średnie arytmetyczne cechy zależnej. Im bardziej zróżnicowane są średnie arytmetyczne tym silniejszy jest związek korelacyjny. Każdy związek korelacyjny jest związkiem stochastycznym.

Każdy związek korelacyjny to stochastyczny, ale nie każdy stochastyczny to korelacyjny.

Metody liczenia związku korelacyjnego:

1. Funkcje regresji - empiryczne funkcje regresji i funkcje regresji pierwszego rodzaju

2. Funkcje teoretyczne, drugiego rodzaju, są na podstawie próby a nie całej zbiorowości

Galton wprowadził funkcję regresji

x- cecha niezależna

, j=1,…u;
, i=1,…z - Te funkcje nie są funkcjami odwrotnymi

Funkcje regresji mogą być pozytywne lub negatywne

Siły związku korealcyjnego

1. STOSUNEK KORELACJI

e_xy - x - cecha niezależna, y- cecha zależna

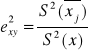
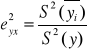
jest zawsze dodatnia

wadą tej miary jest brak kierunku związku korelacyjnego, jest czuła na rozpiętość szeregu statystycznego

zaletą jest: jedna z cech może być niemierzalna (objaśniana), może mierzyć związki o różnych kształtach (np. funkcje wykładnicze)

2. KOWARIANCJA (wariancja wspólna)

zależność cechy x od y

C_xy=C_{yx - kowariancja jest symetryczna}

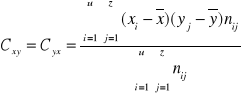
Właściwości kowariancji:

1. jest symetryczna

2. nie zależy od poziomu wag lecz od ich relacji

3. 
   

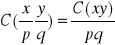
C(x=p,y+q)=C(x,y)

4. posiada dziwne miano

5. Współczynnik korelacji


;



;


Funkcja regresji







Wspólnymi pierwiastkami obu funkcji są
oznacza to, że funkcje w tym punkcie się przecinają





jeśli α=0 tzn. że obie funkcje pokrywają się 0⁰≤ α≤90⁰

jeśli α= 0⁰ następuje związek stochastyczny

jeśli α= 90⁰ następuje niezależność związku korelacyjnego

teoretycznie -∞ ≤ C(xy) ≤ ∞

Kowariancja nie liczy związków nieprostoliniowych

y_i=AB^xi

logy_i=logA+x_ilogB

Współczynnik korelacji liniowej

(Brawas-Pearson)


;-1<r_xy=r_yx<1

współczynnik korelacji jest miarą niemianowaną




obie cechy muszą być mierzalne


jeśli jest to związek liniowy = o

jeśli jest to związek nieliniowy ≠0

KORELACJA WIELORAKA (WIELOKROTNA)

Cecha: 1,2, … n

Rachunek korelacji cząstkowej

Mamy cechy 1,2,3

r_12*3 - zależność cechy 1,2 z wyłączeniem cechy 3










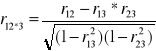
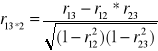
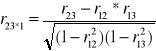
Współczynnik korelacji całkowitej:




R jest zawsze dodatni

0≤R≤1

0 oznacza, że dana cecha nie zależy od innych cech

1 - oznacza, że poznaliśmy wszystkie cechy, które uzależniają daną cechę

jeśli R=0,85 tzn., że wpływ innych czynników na wartość danej cechy wynosi 0,15

wzór uproszczony dla jednej cechy zależnej od dwóch cech







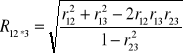
Statystyka Wykłady 2002-11-26, 8:52 a52/p52

4




y od x










Skorelowanie negatywne

Nie ma zw. korelacyjnego, jest zw. stochastyczny

Pozytywne skorelowanie

x od y

x

y







---