Konspekt wykładu 2 (A.Jóźwikowska)
ZBIORY LICZB, KRES DOLNY, KRES GÓRNY
Niech A będzie dowolnym niepustym podzbiorem zbioru R,![]()
.
Zbiór A nazywamy ograniczonym z góry, jeżeli istnieje liczba M taka, że
![]()
.
Kresem górnym zbioru nazywamy najmniejsze z ograniczeń górnych tego zbioru.
Kres górny oznaczamy ![]()
, czytamy supremum A.
![]()
.
Dla zbioru nieograniczonego z góry przyjmujemy, że ![]()
.
Nie należy mylić kresu górnego zbioru z największą liczbą w zbiorze, którą -jeżeli istnieje-oznaczamy ![]()
. Oczywiście ![]()
istnieje wtedy i tylko wtedy, gdy ![]()
i wówczas ![]()
Analogicznie:
Zbiór A nazywamy ograniczonym z dołu, jeżeli istnieje liczba m taka, że
![]()
.
Kresem dolnym zbioru nazywamy największe z ograniczeń dolnych tego zbioru.
Kres dolny oznaczamy ![]()
, czytamy infimum A.
![]()
.
Własności kresu górnego
Jeśli ![]()
, to
a) ![]()
,
b) jeśli ![]()
, to w zbiorze A istnieje element większy od b,
c) jeśli ![]()
, to ![]()
.
Otoczeniem punktu ![]()
o promieniu r (![]()
) nazywamy zbiór
![]()
Otoczeniem plus nieskończoności nazywamy przedział otwarty ![]()
, gdzie a jest dowolną liczbą.
Otoczeniem minus nieskończoności nazywamy przedział otwarty![]()
, gdzie a jest dowolną liczbą.
Sąsiedztwem punktu ![]()
o promieniu r (![]()
) nazywamy zbiór
![]()
![]()
Ciągi Liczbowe
Funkcję odwzorowującą zbiór liczb naturalnych N w zbiór liczb rzeczywistych R
![]()
nazywamy ciągiem liczbowym (nieskończonym) i oznaczamy ![]()
gdzie ![]()
.
![]()
Zasada indukcji matematycznej
Niech ![]()
oznacza twierdzenie dotyczące liczby naturalnej n.
Jeżeli
istnieje, taka liczba naturalna
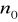
, że twierdzenie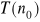
jest prawdziwedla każdej liczby naturalnej
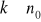
z prawdziwości twierdzenia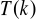
wynika prawdziwość twierdzenia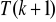
to twierdzenie ![]()
jest prawdziwe dla każdej liczby naturalnej ![]()
.
Przykład
Udowodnić, że dla każdej liczby naturalnej n prawdziwa jest równość
![]()
Ciągi monotoniczne
Ciąg ![]()
jest
![]()
![]()
![]()
![]()
.
Ciągi ograniczone
Ciąg ![]()
jest:
![]()
![]()
![]()
![]()
Granica ciągu
Ciąg zbieżny do granicy skończonej (właściwej)
Def 1:
Liczbę g nazywamy granicą ciągu ![]()
, jeżeli spełniony jest warunek
![]()
.
dla dowolnej liczby dodatniej ![]()
istnieje liczba ![]()
taka, że wszystkie wyrazy ciągu o wskaźnikach większych od ![]()
różnią się od g mniej niż o ![]()
.
Zapisujemy ![]()
lub ![]()
.
Zwrot „Prawie wszystkie wyrazy ciągu” oznacza wszystkie wyrazu ciągu z wyjątkiem co najwyżej skończenie wielu.
Def 1a:
Liczbę g nazywamy granicą ciągu ![]()
, jeżeli w dowolnym otoczeniu liczby g leżą prawie wszystkie wyrazy tego ciągu.
Ciąg, który ma granicę (skończoną) nazywamy zbieżnym.
Zbieżność ciągu oznacza istnienie skończonej granicy tego ciągu.
Ciąg, który nie ma granicy skończonej nazywamy rozbieżnym.
Ciągi rozbieżne
Def 2:
Ciąg ![]()
nazywamy rozbieżnym do ![]()
jeżeli
![]()
dla dowolnej liczby A istnieje liczba ![]()
taka, że wszystkie wyrazy ciągu o wskaźnikach większych od ![]()
są większe od liczby A.
Def 3:
Ciąg ![]()
nazywamy rozbieżnym do ![]()
, jeżeli
![]()
![]()
Zapisujemy
![]()
lub ![]()
.
![]()
lub ![]()
.
Mówimy, że ![]()
, (![]()
) jest granicą niewłaściwą ciągu.
Istnieją ciągi rozbieżne (czyli takie, które nie mają skończonej granicy), które nie są rozbieżne ani do ![]()
ani do ![]()
.
Przykład. Ciąg ![]()
jest rozbieżny.
Rachunek granic skończonych
Tw.
Jeżeli ![]()
i ![]()
, to
1. ![]()
2. ![]()
3. ![]()
przy założeniu, że ![]()
.
Tw. 1
Jeśli ciąg jest zbieżny, to ma dokładnie jedną granicę.
Tw. 2 (dowód)
Jeżeli ciąg jest zbieżny, to jest ograniczony.
Wniosek
Ciąg, który nie jest ograniczony jest ciągiem rozbieżnym.
Uwaga! Twierdzenie odwrotne nie zachodzi.
Ciąg ograniczony, może być ciągiem rozbieżnym.
Tw. 3 (dowód)
Jeżeli ciąg jest monotoniczny i ograniczony, to jest zbieżny.
LITERATURA
Zbiory zadań
Banaś J., Wędrychowicz S., Zbiór zadań z analizy matematycznej, WNT, 1997
Krysicki W., Włodarski L., Analiza matematyczna w zadaniach,t.1, PWN,1998
Stankiewicz W: Zadania z matematyki dla wyższych uczelni technicznych, PWN, 1982
Podręczniki
Żakowski W., Decewicz G., Matematyka cz.I, WNT, (seria podręczników dla elektroniki PW)
R. Leitner, Zarys matematyki wyższej dla inżynierów, Tom I i II, WNT 2000
Gewert M., Skoczylas Z., Analiza matematyczna 1,oficyna wydawnicza GIS,2008,(Politechnika Wrocław)
Dla dociekliwych studentów
Rudnicki R. Wykłady z analizy matematycznej, PWN,2006
G.M. Fichtenholz, Rachunek różniczkowy i całkowy. Tom I i II, PWN, Warszawa 1999.
W. Rudin, Podstawy analizy matematycznej, PWN, Warszawa 2000.
8
Wyszukiwarka
Podobne podstrony:
AM FM SSB Empfänger Teil 1
2006 EGZ WSTĘPNY NA AM
cwiczenie8b am 13 14
2009 EGZ WSTEPNY NA AM ODP(2) Nieznany
AM zaliczenie 4 styczeń 2012 i odpowiedzi wersja B
African am slang
2007 EGZ WSTĘPNY NA AM ODP
sila termoelektryczna, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania),
UMOWY O RATOWNICTWO, AM SZCZECIN, ratownictwo morskie
Rostwory''wejściówka'' teoria, AM, CHEMIA- WICZENIA
83 - 86, AM SZCZECIN, GMDSS ( GOC ), Egzamin
anestezy-wklejone z lepu, AM, rozne, anestezjologia, anestezja
genetyka 2 kolo, AM, rozne, genetyka, genetyka, geny
dusznica bolesna stabilna - ktostam - 4 rok - am bydgoszcz, IV rok Lekarski CM UMK, Kardiologia, Ćwi
Radiotelefon - pytania i odpowiedzi, AM SZCZECIN, GMDSS ( GOC ), wsio
PCR, AM, rozne, genetyka, genetyka, GENETYKA, Genetyka ze strony
odp test 4, AM, rozne, patofizjologia, patofizjo, Patofizjologia
Autyzm wczesnodzieciecy-1, AM, rozne, med rodzinna, Medycyna Rodzinna
więcej podobnych podstron