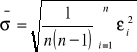Nr ćwiczenia: 303	Data: 28-03-2001r.	Marek Frątczak		Wydział Elektryczny	Semestr II	Grupa: E-9
Prowadzący: mgr Jarosław Gutek			Przygotował: Marek Frątczak	Wykonał: Marek Frątczak	Opracował: Marek Frątczak	Ocena:

Temat: Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego

oraz metodą Bessela.

1. Wstęp teoretyczny.

• Soczewką nazywamy ciało przezroczyste ograniczone dwoma powierzchniami sferyczny-mi.

• Osią optyczną soczewki nazywamy oś łączącą środki krzywizny obu powierzchni soczewki.

• Środkiem optycznym soczewki nazywamy punkt przez który przechodzący promień nie ulega załamaniu niezależnie od kąta padania na soczewkę, doznaje on tylko nieznacznego przesunięcia równoległego.

• Światło przechodzące przez soczewkę ulega kolejno załamaniu na obu jej powierzchniach.

• Ogniskiem nazywamy punkt, w którym skupia się wiązka promieni biegnąca równolegle do osi optycznej .

• Ogniskową nazywamy odległość ogniska od środka soczewki (f).

Położenie ogniska zależne jest od współczynnika załamania n materiału soczewki względem ośrodka, w którym się znajduje, oraz od promieni krzywizn obu powierzchni ograniczających R1 i R2. Zależność ogniskowej f od powyższych parametrów określona jest równaniem:

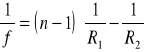
• Ogniskowa układu składającego się z dwóch soczewek cienkich o ogniskowych f1 i f2, znajdujących się we wzajemnej odległości d wyraża się wzorem:

• Zdolność skupiająca soczewki - jest to odwrotność ogniskowej (
  ).

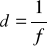
• Dioptria - jest to jednostka zdolności skupiającej [m^-1].

• Równanie soczewkowe - określa ono położenie obrazu zależne od położenia przedmiotu oraz od ogniskowej soczewki:

,

gdzie p jest odległością przedmiotu od soczewki, o - odległość obrazu od soczewki.

• Warunki stosowania równania soczewkowego:

- promienie wybiegające z P tworzą niewielki kąt z osią optyczną,

- soczewka jest cienka, tzn. jej grubość jest mała w porównaniu z promieniami krzywizny.

• Znaki wielkości występujących w równaniu soczewkowym:

- p jest zawsze dodatnie,

- o, R oraz f są dodatnie, gdy leżą po przeciwnej stronie soczewki niż przedmiot,

- o, R i f są ujemne, gdy leżą po tej samej stronie co przedmiot.

• Powiększeniem liniowym nazywamy stosunek wielkości obrazu do wielkości przedmiotu. Jest on także równy stosunkowi odległości o i p

Znak „-„ został wprowadzony po to, żeby powiększenie było dodatnie, gdy obraz jest prosty, a ujemne, gdy odwrócony.

• Metoda Bessela

Fizyczną konsekwencją symetrii równania soczewkowego jest możliwość uzyskania ostrego obrazu przy dwóch położeniach soczewki względem przedmiotu.Przy stałej odległości l przedmiotu od ekranu obraz powstaje w odległości o oraz o' = p od soczewki. Przy jednym położeniu obraz jest pomniejszony, a przy drugim powiększony w stosunku do przedmiotu.

Ogniskowa soczewki wyznaczona metodą Bessela.

Aby wyznaczyć ogniskową soczewki lub układu soczewek z powyższego równania należy zmierzyć odległość przedmiotu od ekranu l odległość e między dwoma położeniami soczewki, przy których obraz na ekranie jest ostry.

l = o + p - odległość przedmiotu od ekranu

e = o - p - odległość między dwoma położeniami soczewki

2. Opis przeprowadzonego ćwiczenia.

• Umieścić badaną soczewkę w uchwycie ruchomego wózka.

• Dobierając położenie soczewki doprowadzić do uzyskania ostrego obrazu na ekranie.

• Wyznaczyć odległość przedmiotu i obrazu od soczewki dla kilku położeń. Pomiary przeprowadzić dla soczewek skupiających i układu: soczewka skupiająca + soczewka rozpraszająca.

• Dla każdego położenia ekranu obliczyć ogniskową ze wzoru soczewkowego i następnie wartości średnie dla każdej z soczewek.

• Dla tych samych soczewek zastosować metodę Bessela. Zmierzyć odległość l oraz e dla różnych położeń ekranu.

• Obliczyć ogniskowe soczewek skupiających i układu ze wzoru:
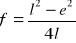
  oraz ogniskową soczewki rozpraszającej z równania: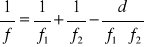
  .

• Obliczyć wartość średniej dla każdej soczewki.

3. Dane eksperymentalne.

Dla soczewki skupiającej „C”:

• Z równania soczewkowego

L.p.	p	o		WART.ŚREDNIA	BŁ. ŚR. KWAD. ŚRED. ARYTM.	surowy wynik pomiaru dla średniej
1.	249	551	171,50	171,85	0,01745667	171,85±0,01745667
2.	249,5	550,5	171,69
3.	250	550	171,87
4.	250,5	549,5	172,06
5.	250	550	171,87
6.	250,5	549,5	172,06
7.	249,5	550,5	171,69
8.	250	550	171,87
9.	250,5	549,5	172,06
10.	250	550	171,87

• Metoda Bessela

L.p.	e	l		WART.ŚREDNIA	BŁ. ŚR. KWAD. ŚRED. ARYTM.	surowy wynik pomiaru dla średniej
1.	351,5	800	161,39	161,51	0,01857481	146,44±0,01857481
2.	352	800	161,28
3.	351	800	161,50
4.	350	800	161,71
5.	351,5	800	161,39
6.	350	800	161,71
7.	350,5	800	161,61
8.	351	800	161,50
9.	351	800	161,50
10.	351	800	161,50

Dla układu soczewek „C i 3”:

• Z równania soczewkowego

Lp.	d	p	o	fs	f3	f	WART. ŚREDNIA	BŁ. ŚR. KWAD. ŚRED. ARYTM.	surowy wynik pomiaru dla średniej
1.	8	171,5	628,5	171,85	594,71	134,73	135,13	0,02220064	135,13±0,02220064
2.	8	172,5	627,5	171,85	606,54	135,3
3.	8	172	628	171,85	600,68	135,02
4.	8	171,5	628,5	171,85	598,71	134,73
5.	8	172,5	627,5	171,85	606,54	135,3
6.	8	172	628	171,85	600,68	135,02
7.	8	173	627	171,85	612,70	135,59
8.	8	172,5	627,5	171,85	606,54	135,3
9.	8	172	628	171,85	600,68	135,02
10.	8	172,5	627,5	171,85	606,54	135,3

• Metoda Bessela

Lp.	d	e	l		WART.ŚREDNIA	BŁ. ŚR. KWAD. ŚRED. ARYTM.	surowy wynik pomiaru dla średniej
1.	8	512,5	800	117,92	117,98	0,00439934	117,98±0,00439934
2.	8	512	800	118,08
3.	8	512	800	118,08
4.	8	513	800	117,76
5.	8	512,5	800	117,92
6.	8	512,5	800	117,92
7.	8	512	800	118,08
8.	8	511,5	800	118,24
9.	8	512,5	800	117,92
10.	8	512,5	800	117,92

4. Przykładowe obliczenia.

5. Zestawienie wyników.

Dla ogniskowej soczewki skupiającej:

• Ze wzoru soczewkowego:

f_c =171,85±0,01745667 mm

• Metodą Bessel'a:

f_c =146,44±0,01857481 mm

Dla układu soczewek C+3 :

• Ze wzoru soczewkowego:

f₃=135,13±0,0222006

• Metodą Bessel'a:

f₃ =117,98±0,00439934

6. Wnioski.

Celem powyższego ćwiczenia było zmierzenie wartości ogniskowych soczewek z równania soczewkowego oraz metodą Bessela. Otrzymane wartości zestawione zostały powyżej. Widać, że otrzymane wartości z równania soczewkowego różnią się od wartości z metody Bessela. Błędy pomiarowe wynikały z ograniczonych możliwości ludzkiego oka (tzn. chodzi tu o jednakowe odczytanie ostrości obrazu za każdym pomiarem), jednak różnice w pomiarach były niewielkie. Z tego powodu wynikają błedy w obliczeniach.

---