Nr ćwiczenia 74 |
Temat ćwiczenia Polarymetr |
Ocena z teorii |
Nr zespołu 10 |
Imię i Nazwisko Miłosz Gąsiorowski |
Ocena z wykonania |
Data 20.02.2001 |
Wydział, kierunek, rok, grupa EAIiE, Automatyka i Robotyka, rok 1, gr.2 |
Uwagi |
Konspekt.
Celem ćwiczenia jest wyznaczanie kąta skręcenia płaszczyzny kąta polaryzacji oraz wykorzystanie tego zjawiska do wyznaczania stężenia roztworów cukru i grubości płytek z materiałów optycznie czynnych wpierw wzorcując przyrząd posiadanymi wzorcami.
Zapoznanie się z podstawą teoretyczną ćwiczenia.
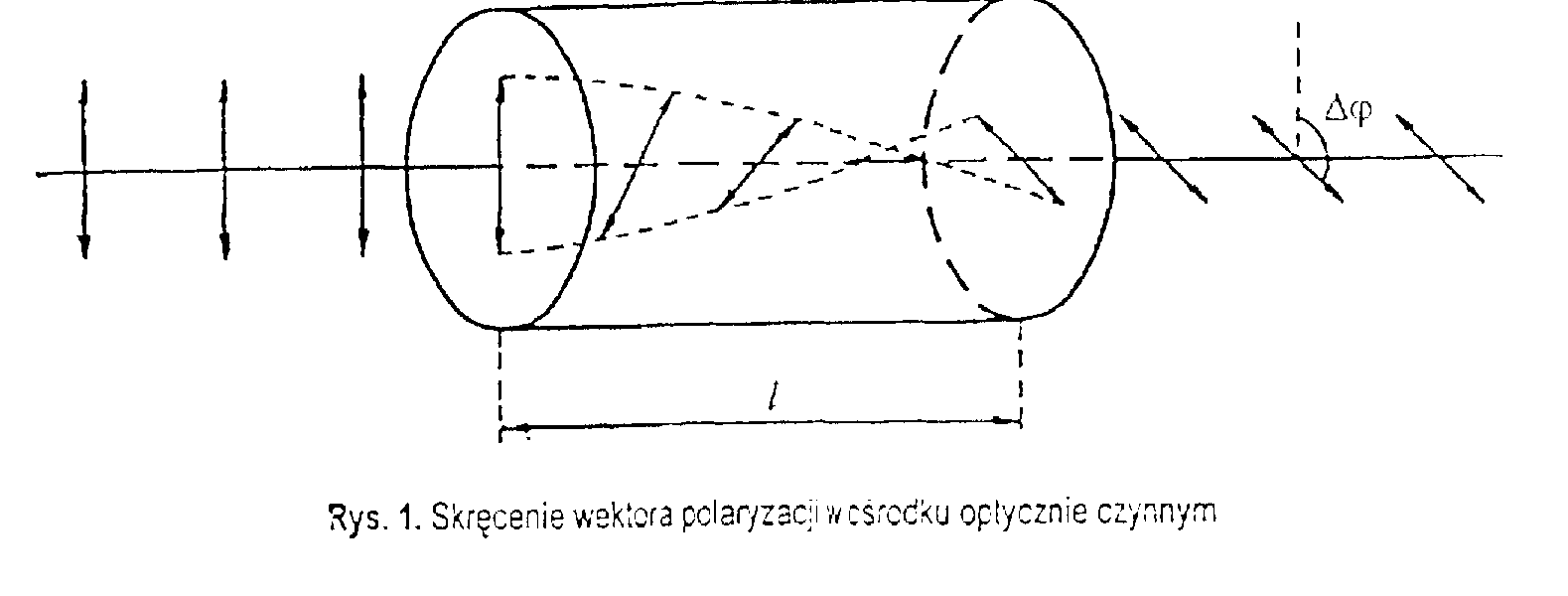
Światło liniowo spolaryzowane rozchodzi się bez zmiany płaszczyzny polaryzacji w próżni i w większości ośrodków przeźroczystych. Istnieją jednak ośrodki zwane optycznie aktywnymi, które wywołują skręcenie kierunku polaryzacji. Wektor E fali elektromagnetycznej w tych ośrodkach nie leży w jednej płaszczyźnie, lecz zatacza linie śrubową.
Skręcenie wektora polaryzacji w ośrodku optycznie czynnym
Wyjaśnienie mechanizm skręcenia wektora polaryzacji rozważyć można przy pomocy wyimaginowanej cząsteczki w kształcie śruby. Padające światło w kierunku osi y posiada pole Ey poruszające ładunkami w górę i w dół po lini śrubowej. W skutek więzów cząsteczkowych elektrony muszą pozostawać na linii śrubowej, czyli także w kierunku x .
Tak więc powstaje dodatkowa x składowa pola elektrycznego, która w wyniku superpozycji daje wypadkową zrotowaną do padającej o mały kąt
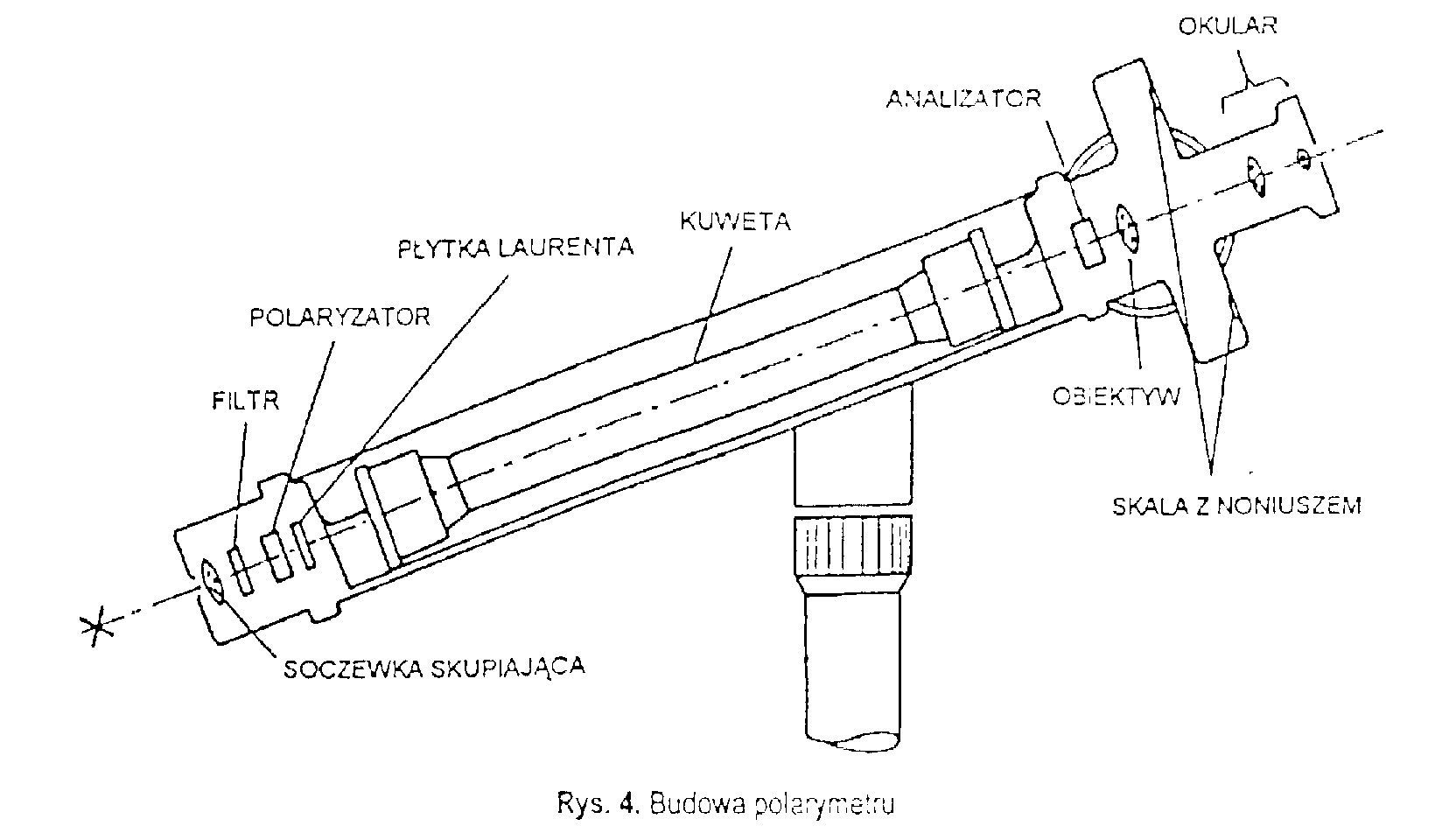
Zapoznanie się z budową przyrządu
Budowa polarymetru
Pomiar stężenia
Dla niezbyt dużych stężeń przyjąć można, że kąt skręcenia płaszczyzny polaryzacji będzie proporcjonalny do liczby cząstek, jakie napotka światło na swojej drodze. Oznacza to, że kąt skręcenia płaszczyzny polaryzacji będzie proporcjonalny do długości l i stężenia roztworu c:
k·c·l
Współczynnik proporcjonalności k nazywamy skręceniem właściwym roztworu
Dla substancji stałych możemy wykorzystać do wyznaczanie grubości płytek gdyż kąt skręcenia jest proporcjonalny do grubości:
k1·l
Wykonanie:
Ustawić położenie zerowej polarymetru.
Pomiar grubości płytki (pomiar polegający na wykorzystaniu znanych wzorców):
Ustawić pusty polarymetr w pozycji zerowej- 0, powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla płytek o znanych grubościach z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytek o znanych grubościach- =0o zacząć od najcieńszej, pomiar powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla płytki o nieznanej grubości, z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytki o nieznanej grubości- =0, pomiar powtórzyć 5-10 razy
Wyznaczyć prostą regresji dla otrzymanych pomiarów metoda najmniejszych kwadratów, wyliczyć współczynniki prostej.
Metodą interpolacji wyznaczyć grubość płytki.
Pomiar stężenia roztworu (pomiar polegający na wykorzystaniu znanych wzorców):
Ustawić położenie zerowe dla kuwety z rozpuszczalnikiem- 0, powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla kuwet z roztworami o znanych stężeniach z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla płytek o znanych grubościach- =0 zacząć od najcieńszej, pomiar powtórzyć 5-10 razy
Wyznaczyć położenie dla których pole jest zaciemnione rownomiernie- dla kuwety z roztworem o nieznanym stężeniu, z tego wyznaczyć kąt skręcenia płaszczyzny polaryzacji dla kuwety z roztworem o nieznanym stężeniu - =0, pomiar powtórzyć 5-10 razy
Wyznaczyć prostą regresji dla otrzymanych pomiarów metoda najmniejszych kwadratów, wyliczyć współczynniki prostej.
Metodą interpolacji wyznaczyć stężenie roztworu.
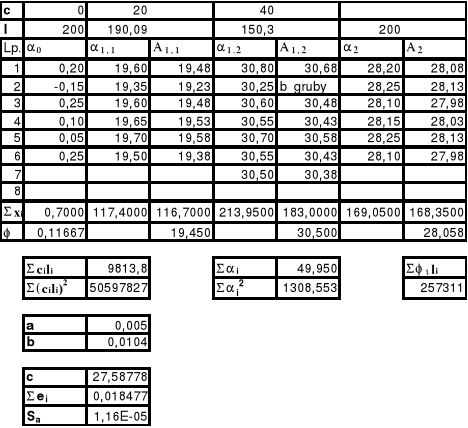
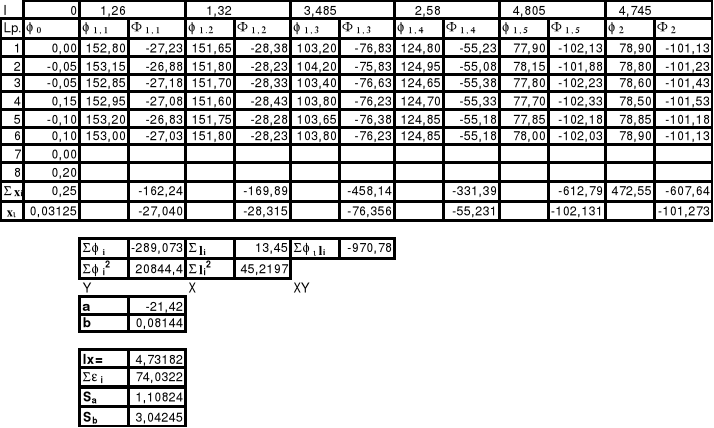
Tabela pomiarów-wyznaczanie grubości płytki
Lp. |
0 |
, |
, |
, |
, |
, |
, |
, |
, |
, |
, |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
xi2 |
|
|
|
|
|
|
|
|
|
|
|
Lp. |
1.6 |
, |
, |
, |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
xi |
|
|
|
|
|
|
xi2 |
|
|
|
|
|
|
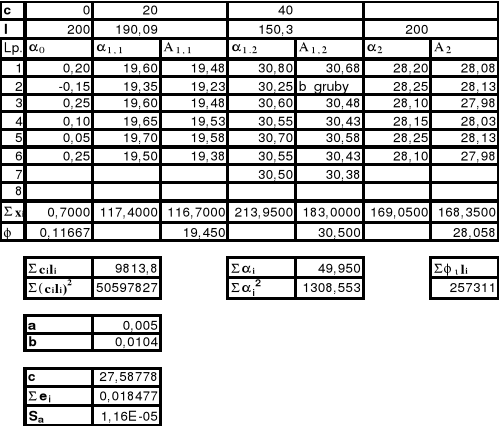
Tabela pomiarów-wyznaczanie stężenia roztworów
Lp. |
0 |
, |
, |
, |
, |
, |
, |
, |
, |
, |
, |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
xi2 |
|
|
|
|
|
|
|
|
|
|
|
Lp. |
1.6 |
, |
, |
, |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
xi |
|
|
|
|
|
|
xi2 |
|
|
|
|
|
|
Stosujemy metodę wyrównawczą Gaussa do analizy wyników (wynik najmniejszych kwadratów):
Ogólna zależność wyników w zależności liniowej
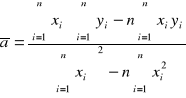
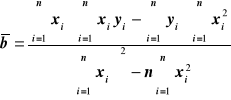
![]()
Wzory na wyliczenie współczynników zależności liniowej, mając n par punktów pomiarowych xi yi zależnych liniowo.
![]()
Sposób wyliczenia odchylenia standardowego
![]()
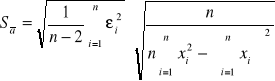
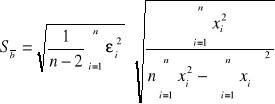
Jeżeli znajdziemy współczynniki a i b znając obliczymy l oraz odchylenie standardowe Sa
![]()
![]()
gdyż
identycznie jeżeli będziemy znali średnie obliczymy stężenie cx
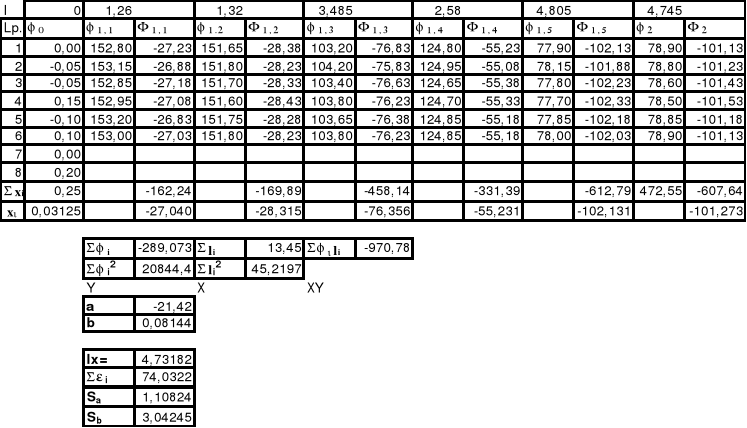
Błąd wyznaczanie zarówno stężenia roztworu zależy od kilku zmiennych tak wiec błędy będziemy wyznaczać metodą różniczki zupełnej
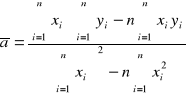
![]()
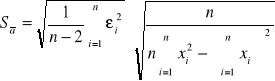
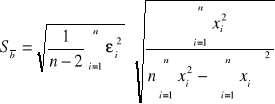
![]()
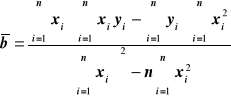
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Lab 8 - Polarymetr, sprawozdanie Magdy 74, GRUPA 10
Sprawka Lab, Bomba Kalorymetryczna - spr, Ćwiczenie nr:
Nr ćwiczenia, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 10 Badanie
lab fiz sem 5, lab 4b, Nr ćwiczenia : 4
Lab 8 - Polarymetr, Cwiczenie 074, Nazwisko i imię:
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Nr ćwiczenia
Zaliczenie nr 1 ćwiczenie 4E
Sprawozdanie nr 3 Ćwiczenie M 8
Ćw nr 9, ćwiczenie 9, Paweł karaś
galwanotechnika, ĆWICZENIE NR 3, ĆWICZENIE NR 3
Lab 4 - Gazoprzepuszczalność, SKALY4R, Nr. ˙wiczenia
LABFIZ 1(2), Nr ćwiczenia:
cw14sk , Nr ćwiczenia:
Nr ćwiczenia02(1)
Sprawozdanie nr 1 Cwiczenie E 3
Nr Ćwiczenia 6
54+, Politechnika Rzeszowska, Elektrotechnika, semestr 2, Fizyka Lab, Sprawozdania, Fizyka Laborator
więcej podobnych podstron