31

Rozdział 2

Konstrukcje geometryczne

32

Przez ponad dwa tysiące lat do najważniejszych problemów w matematyce zaliczane były

problemy konstrukcyjne. W Akademii Platońskiej ustalono kanon postępowania z zadaniami kon-
strukcyjnymi za pomocą klasycznych dziś środków konstrukcyjnych: cyrkla i linijki. Starożytni
sformułowali też wiele problemów, które ostatecznie zostały rozwiązane dopiero w XIX w.

Obecnie konstrukcje już nie należą do najważniejszych zagadnień matematyki. W dalszym

ciągu jednak zadania konstrukcyjne odgrywają istotną rolę w poznawaniu klasycznej geometrii
i matematyki w ogóle.

Przypomnij sobie, jakie konstrukcje wykonywałeś do tej pory na lekcjach geometrii.
Opisz tok postępowania podczas rozwiązywania zadania konstrukcyjnego.
Wykonaj i dokładnie opisz jedną ze znanych ci konstrukcji.

Konstrukcje geometryczne zrodziły się najprawdopodobniej z rozwiązywania problemów

praktycznych, m.in. związanych z odtwarzaniem podziału gruntów po wylewach rzek i powo-
dziach – geometria rozwijała się najszybciej w cywilizacjach powstałych nad wylewają-
cymi często rzekami. Podziały kątów i odcinków, konstrukcje różnych wielokątów – były
to typowe zadania, z którymi stykali się rzemieślnicy różnych zawodów. Dopiero jednak staro-
żytni Grecy ustalili kanon postępowania z zadaniami konstrukcyjnymi, który w zasadzie obo-
wiązuje do dziś.

Najpierw zadanie należy precyzyjnie określić. Rozpatrzmy to na przykładzie konstrukcji pro-

stej stycznej do okręgu: chcemy przez zadany punkt na płaszczyźnie poprowadzić prostą styczną
do okręgu.

Określamy zatem

dane

: punkt i okrąg na płaszczyźnie.

Ustalamy, co chcemy skonstruować (dawniej używany był termin

szukane

): styczną do dane-

go okręgu przechodzącą przez zadany punkt.

Trzeba jeszcze ustalić

środki konstrukcyjne

: linijka i cyrkiel.

33

2. KONSTRUKCJE GEOMETRYCZNE

U

WAGA

Powróćmy do zadania.
Wzorcowe rozwiązanie zadania przebiega w czterech etapach:

1. analiza zadania,
2. opis konstrukcji,
3. dowód poprawności konstrukcji,
4. dyskusja.

Zacznijmy od analizy zadania. Zazwyczaj polega ona na dokładnym przyjrzeniu się danym

i wykorzystaniu własności pewnych figur. Można też określić własności obiektów, które dopiero
mają być skonstruowane.

Nasze zadanie polega na skonstruowaniu stycznej do okręgu,

ale w sformułowaniu zadania nie jest wyraźnie zaznaczone, gdzie
leży punkt, z którego mamy poprowadzić prostą styczną. Należy
więc rozpatrzyć trzy przypadki. Jeden odrzucamy natychmiast:
gdy punkt leży wewnątrz koła, styczna nie istnieje.

Zajmijmy się przypadkiem, gdy punkt leży na zewnątrz koła.

Przyjrzyjmy się rysunkowi, na którym styczna już jest poprowa-
dzona.

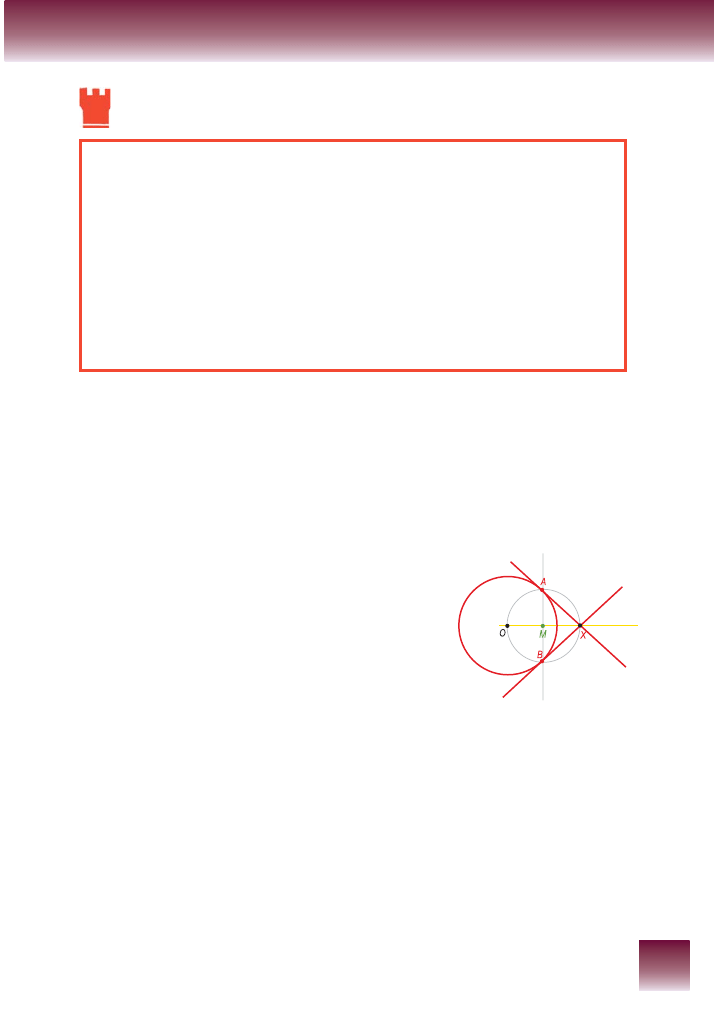
Zauważmy, że dany punkt X, środek okręgu O oraz punkt styczności A wyznaczają trójkąt

prostokątny (dlaczego?). Jeśli potrafimy skonstruować ten trójkąt, to potrafimy również skon-
struować styczną.

Jak skonstruować trójkąt prostokątny, gdy mamy jego przeciwprostokątną? Wykorzystajmy

własności kąta prostego wpisanego w okrąg.

Oto opis konstrukcji (w uproszczeniu):

– łączymy prostą punkty X i O,
– znajdujemy środek M odcinka XO,
– zakreślamy okrąg o środku M i promieniu XM,
– punkty przecięcia tego okręgu z okręgiem wyjściowym są punktami styczności poszukiwanej

prostej; prowadzimy prostą przez punkt X i jeden z tych punktów.

Można zadać pytanie, dlaczego środków konstrukcyjnych nie zaliczymy do danych.
Między danymi a środkami konstrukcyjnymi występuje pewna subtelna różnica. Dane to
figury, którymi dysponujemy na początku konstrukcji: punkty, proste, odcinki, okręgi itp.
Natomiast środki konstrukcyjne to sposoby dołączania nowych figur do danych.
Jeśli mówimy, że mamy linijkę, to nie chodzi nam o kawałek drewna lub plastiku z podziałką,
tylko o możliwość połączenia dwóch punktów fragmentem linii prostej lub narysowania do-
wolnego fragmentu prostej. W praktyce nie mówimy o fragmencie lub odcinku prostej, tylko
o prostej.
Podobnie, gdy dany jest cyrkiel, tzn., że z dowolnego punktu możemy wykreślić okrąg o za-
danym promieniu albo po prostu taki okrąg można zaliczyć do zbioru danych.

Cyrkiel i linijkę nazywamy

klasycznymi środkami konstrukcyjnymi

, a konstrukcje powsta-

łe za ich pomocą

konstrukcjami klasycznymi

albo

konstrukcjami platońskimi

.

34

2. KONSTRUKCJE GEOMETRYCZNE

Dlaczego konstrukcja jest poprawna? W zasadzie poprawność wynika z analizy zadania: pro-

sta przechodząca przez punkty X i A jest prostopadła do odcinka OA, ponieważ kąt XAO jest
prosty jako oparty na średnicy okręgu.

W czwartym etapie rozwiązywania zadania poświęconym dyskusji rozważa się różne pytania

dotyczące istnienia rozwiązania, jego jednoznaczności, liczby rozwiązań, możliwości uogólnień
itp. Można też analizować różne szczególne sytuacje.

W zadaniu o prostej stycznej do okręgu widzimy, że gdy punkt leży na zewnątrz koła, to

mamy dwa rozwiązania – możemy skonstruować dwie proste styczne. Gdy punkt leży na okręgu,
styczna w tym punkcie będzie tylko jedna.

Z

ADANIE

Przeanalizuj dokładnie przypadek, gdy punkt leży na okręgu.

Pojawia się pytanie o proste styczne do dwóch okręgów. Proponujemy to jako temat innego

zadania.

Zanim przejdziemy do kolejnych zadań, przypomnijmy najważniejsze konstrukcje, które mogą

być znane z wcześniejszej nauki.

Są to:

– konstrukcja prostej prostopadłej do danej prostej i przechodzącej przez zadany punkt,
– konstrukcja prostej równoległej do danej prostej i przechodzącej przez zadany punkt,
– konstrukcja symetralnej odcinka,
– konstrukcja środka odcinka,
– konstrukcja dwusiecznej kąta,
– podział odcinka na kilka równych części,
– konstrukcja kwadratu o zadanym boku,
– konstrukcja trójkąta równobocznego o zadanym boku,
– konstrukcja trójkąta o zadanych bokach.

Z

ADANIE

Jeśli nie znasz którejś z powyższych konstrukcji, to potraktuj jej wykonanie lub znalezienie sposo-
bu jej wykonania (samodzielnie lub w literaturze) jako zadanie.

Zauważmy, że wiele zadań i twierdzeń z geometrii można sprowadzić do zadań konstrukcyjnych.

Przejdźmy do przykładów. W poprzednim rozdziale mówiliśmy o okręgach wpisanych w trójkąt

i opisanych na trójkącie. Zdobytą wiedzę możemy przetestować w następujących przykładach.

P

RZYKŁAD

1

Dany jest trójkąt; skonstruuj okrąg opisany na tym trójkącie.

Idea rozwiązania: konstruujemy symetralne dwóch boków, ich punkt przecięcia jest poszuki-

wanym środkiem okręgu.

Uzasadnij pisemnie poprawność tej konstrukcji.

Równie proste jest rozwiązanie kolejnych zadań.

35

2. KONSTRUKCJE GEOMETRYCZNE

Z

ADANIE

Dany jest trójkąt; skonstruuj okrąg wpisany w ten trójkąt.

P

RZYKŁAD

2

Dane są dwa okręgi; skonstruuj styczną do tych okręgów.

Rozważmy jedynie przypadek, gdy okręgi są zewnętrznie rozłączne.
Podamy tylko opis konstrukcji, a Ty, drogi Czytelniku, spróbuj przeanalizować tę konstrukcję

i uzasadnić jej poprawność.

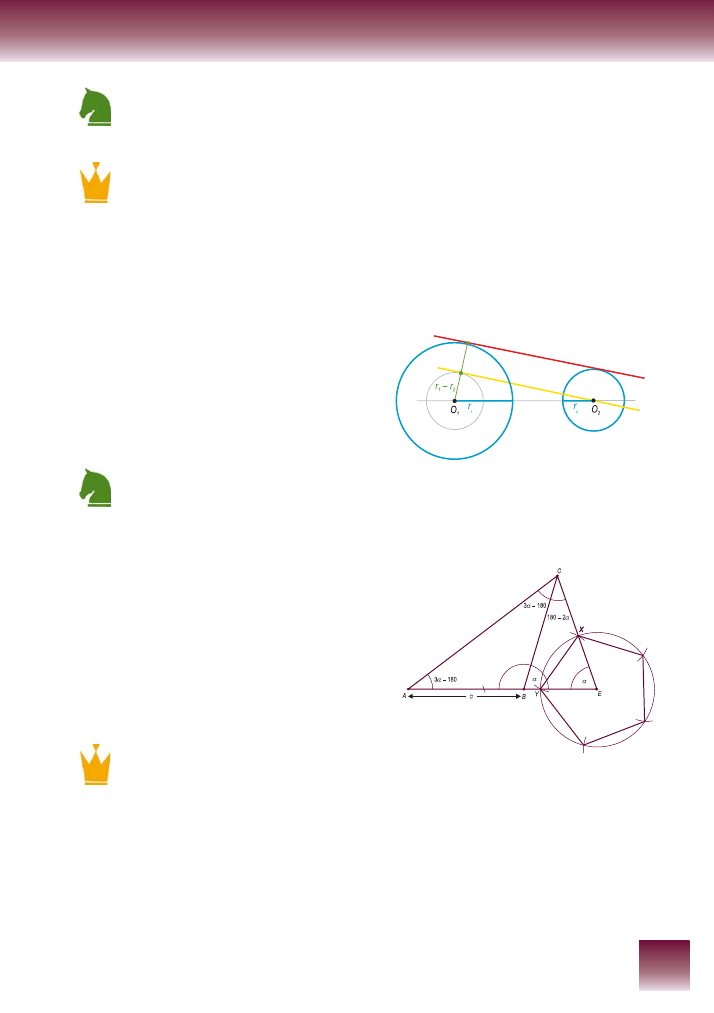
Przypomnijmy dane: okrąg

o O r

1 1

(

)

,

i okrąg

o O r

2

2

(

)

,

;

r

r

1

2

>

.

Najpierw konstruujemy okrąg

o O r r

1

1

2

(

)

−

,

.

Następnie konstruujemy styczną do tego okręgu

z punktu O

2

.

Przez punkt styczności i punkt O

1

prowadzimy

prostą.

Konstruujemy prostopadłą do tej prostej w punk-

cie jej przecięcia z okręgiem o(O

1

, r

1

). Jest to poszuki-

wana styczna.

Z

ADANIE

Przeanalizuj różne inne przypadki z powyższego przykładu w zależności od wzajemnego położenia
dwóch okręgów. Ile można skonstruować stycznych do dwóch danych okręgów? Jak te styczne będą
położone?

Konstrukcje trójkątów

Cała seria zadań konstrukcyjnych dotyczy trójkątów.
Zazwyczaj podajemy w nich trzy dane, a gdy chce-

my skonstruować trójkąt równoramienny – dwie dane.
W starszych zbiorach zadań dane podaje się, stosując
standardowe oznaczenia dla trójkąta (np. bok a leży
naprzeciwko wierzchołka A).

P

RZYKŁAD

3

Skonstruuj trójkąt, gdy dane są dwa boki i kąt.

Dane są: a, b i

γ

) lub a, b i

α

.

)

Rozwiążmy zadanie, zakładając, że dane są a, b i

α

.

)

Na prostej odkładamy odcinek o długości a.
W jednym z końców tego odcinka odkładamy

α

.

)

Konstruujemy okrąg o środku w drugim końcu odcinka i o promieniu a.
Punkt przecięcia okręgu i drugiego ramienia kąta wyznaczy trzeci wierzchołek trójkąta.

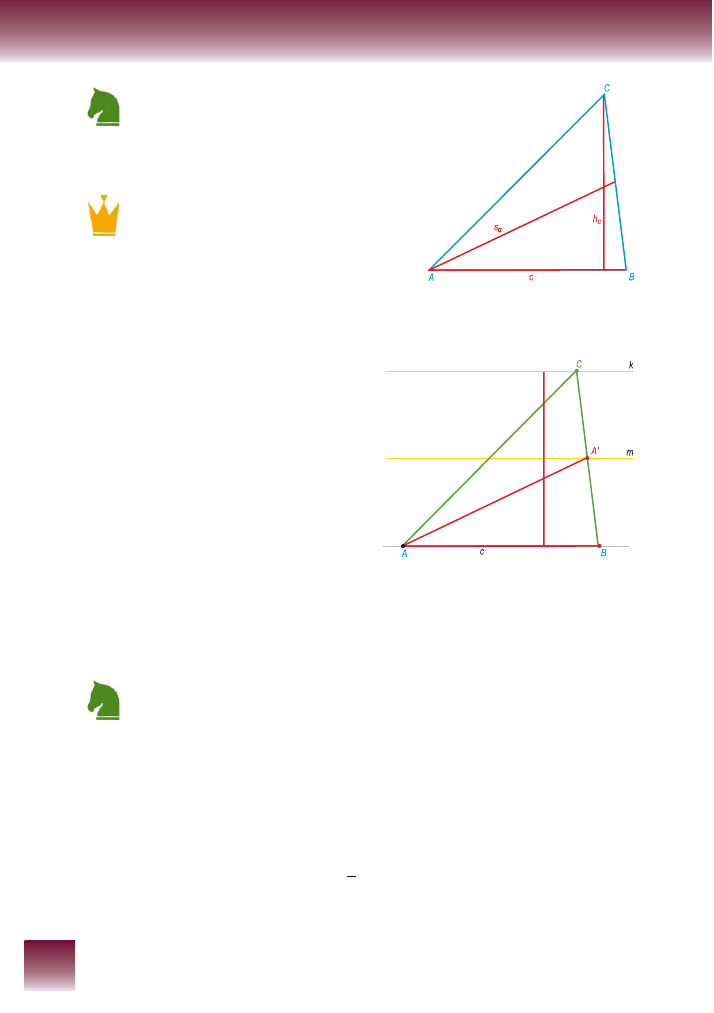
36

2. KONSTRUKCJE GEOMETRYCZNE

Z

ADANIE

Skonstruuj trójkąt, gdy dane są a,

α

)

,

β

.

)

I jeszcze jeden przykład.

P

RZYKŁAD

4

Dane są c, h

c

, s

a

.

Skonstruuj trójkąt.

Przyglądając się rysunkowi, widzimy, że dane są dwa

wierzchołki trójkąta wraz z odcinkiem c. Za pomocą wysokości h

c

wyznaczymy prostą, na której

będzie leżał trzeci wierzchołek, a za pomocą s

a

środek jednego z boków.

Opis konstrukcji jest następujący:

– na prostej odkładamy odcinek AB o długości c,
– konstruujemy prostopadłą do tej prostej,
– na prostopadłej odkładamy wysokość h

c

tak, żeby

jeden jej koniec leżał na prostej zawierającej AB,

– przez drugi koniec wysokości prowadzimy pro-

stą k równoległą do AB,

– wyznaczamy środek wysokości h

c

i konstruujemy

równoległą do AB prostą m przechodzącą przez
ten środek,

– konstruujemy okrąg, którego środek jest jednym

z końców odcinka AB – np. A, a promień jest
równy s

a

,

– przez punkt A

′, w którym okrąg przecina się

z prostą m, i przez punkt B prowadzimy prostą,

– punkt przecięcia tej prostej z prostą k jest poszukiwanym trzecim wierzchołkiem konstruowa-

nego trójkąta.

Uzasadnienie poprawności konstrukcji proponujemy jako zadanie.

Ostatni przykład można uogólnić.

Z

ADANIE

W trójkącie dany jest jeden z boków, wysokość i środkowa. Skonstruuj ten trójkąt.

W omawianych przykładach milcząco zakładamy, że dane są tak dobrane, iż konstrukcja

trójkąta jest możliwa, np. długość s

a

jest taka, że istnieje punkt przecięcia odpowiedniego okręgu

z prostą m.

Proponujemy przeanalizowanie przykładów właśnie pod kątem takiego doboru danych – dłu-

gości odcinków – żeby konstrukcję można było wykonać.

W przykładzie 4 na pewno musi być

c

s

h

1
2

≥

a

.

Czy to już wystarczy, żeby konstrukcja mogła

być wykonana?

37

2. KONSTRUKCJE GEOMETRYCZNE

* Przyjrzyjmy się jeszcze jednej konstrukcji.

P

RZYKŁAD

5

W trójkącie równoramiennym dany jest bok i promień okręgu wpisanego. Skonstruuj ten trójkąt.

Mamy tu dwa przypadki do rozpatrzenia.

Pierwszy przypadek: dany bok jest podstawą trójkąta równoramiennego.
Konstrukcja może wyglądać tak:

– ze środka podstawy prowadzimy prostopadłą,
– odkładamy na niej promień tak, by jeden jego koniec leżał na podstawie,
– z drugiego końca promienia zakreślamy okrąg o tym promieniu,
– z końców podstawy prowadzimy styczne do okręgu,
– punkt przecięcia stycznych wyznacza wierzchołek trójkąta równoramiennego.

Bez trudu zauważamy, że promień okręgu wpisanego musi być krótszy od połowy podstawy,

żeby konstrukcja była możliwa.

Drugi przypadek: dany bok jest ramieniem trójkąta.
Tu spotyka nas przykra niespodzianka. Konstrukcji nie da się wykonać! Nie dlatego, że dane

są źle dobrane. Po prostu za pomocą cyrkla i linijki nie możemy skonstruować poszukiwanego
trójkąta. Można to udowodnić, wykorzystując odpowiednie teorie matematyczne.

Istnieją więc dające się prosto sformułować zadania, których nie można rozwiązać za pomo-

cą klasycznych środków.

U

WAGA

U

WAGI

HISTORYCZNE

Kanon postępowania przy rozwiązywaniu zadań konstrukcyjnych, a także dobór środ-
ków konstrukcyjnych zostały ustalone w Akademii Platońskiej. W starożytności i jesz-
cze długo później panowało przekonanie, że za pomocą cyrkla i linijki można rozwią-
zać wszystkie zadania konstrukcyjne, chociaż starożytni Grecy znali problemy, któ-
rych nie umieli rozwiązać środkami im dostępnymi. Dopiero w XIX w. został stworzony
odpowiedni aparat matematyczny, który umożliwiał sprawdzenie, czy konkretny pro-
blem jest rozwiązywalny za pomocą środków klasycznych, czy też nie.

Akademia Platońska, założona w V w. p.n.e. przez jednego z największych

filozofów starożytności Platona, może być uznana za pierwszą wyższą uczelnię.
Nazwę swą zawdzięcza gajowi Akademosa, gdzie spotykali się pierwsi jej założy-

ciele. Przetrwała ponad tysiąc lat i została rozwiązana dopiero na początku VI w. na

mocy dekretu cesarza Bizancjum Justyniana.

Sam Platon (428–347 p.n.e.), autor wielu rozpraw filozoficznych, nie napisał żadnego dzieła

matematycznego, chociaż jego nazwisko na trwałe weszło do matematyki; mówimy dziś o kon-
strukcjach platońskich i bryłach platońskich. Używany jest też przyrząd konstrukcyjny nazywany
krzyżakiem Platona.

Należy odróżnić niemożność wykonania konstrukcji z powodu nieistnienia konstruowanego
obiektu (bo np. dane są źle dobrane) od niewykonalności konstrukcji ze względu na to, że
środki są niewystarczające. Konstrukcja, której jeszcze nikt nie wykonał, to „konstrukcja nie-
wykonana”, a nie „konstrukcja niewykonalna” (co często bywa mylone).

Platon

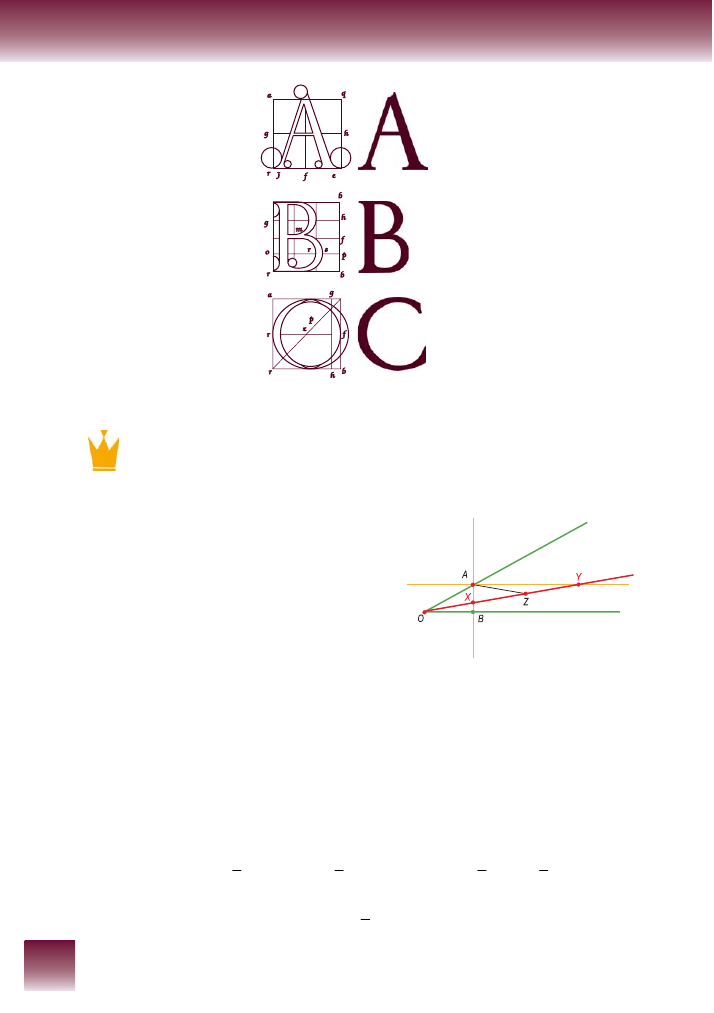
38

2. KONSTRUKCJE GEOMETRYCZNE

Oto jeden z przykładów zadań, których nie można rozwiązać środkami klasycznymi.

P

RZYKŁAD

6 (

TRYSEKCJA

KĄTA

)

Dany kąt podziel na trzy równe części.

Konstrukcję wykonamy środkami nieklasycznymi.

Na jednym z ramion kąta o wierzchołku O wybierz-

my punkt A i poprowadźmy przez niego prostą równo-
ległą i prostą prostopadłą do drugiego ramienia. Pro-
sta prostopadła przecina drugie ramię w punkcie B.
Teraz na linijce zaznaczmy punkty X i Y takie, że
|XY|=2|OA|. Za pomocą tej linijki poprowadźmy pro-
stą przez punkt O w taki sposób, żeby punkt X leżał na
AB, a punkt Y na prostej równoległej do ramienia OB.

Kąt XOB jest poszukiwanym kątem.

Choć posługujemy się tylko cyrklem i linijką, konstrukcja nie jest klasyczna, bo linijka ma

wyróżnione punkty.

Uzasadnienie opiera się na wykorzystaniu własności kątów w trójkącie i kątów naprzemian-

ległych.

Na odcinku XY wybieramy teraz środek Z i łączymy z punktem A.
Zauważamy, że |OA|=|XZ|=|ZY|=|ZA| (dlaczego?), czyli trójkąty OAZ i AZY są równora-

mienne.

W związku z tym

XOB

AYZ

AZY

AZO

AZO

AOZ

1

1

1

1

(180

)

(180 (180

))

2

2

2

2

=

=

−

=

−

−

=

=

,

)

)

)

)

)

)

czyli

XOB

AOB

1

.

3

=

)

)

39

2. KONSTRUKCJE GEOMETRYCZNE

U

WAGA

Podamy jeszcze przykład zadania, w którym wykorzystamy tylko cyrkiel.

P

RZYKŁAD

7

Skonstruuj za pomocą samego cyrkla sześciokąt foremny wpisany w dany okrąg.

Oczywiście, skonstruować możemy tylko wierzchołki tego sześcioką-

ta, bo nie mamy linijki.

Konstrukcja jest powszechnie znana. Na danym okręgu zaznaczamy

z wybranego punktu łuk okręgu o tym samym promieniu, następnie
z punktu przecięcia tego łuku z okręgiem jeszcze raz zakreślamy taki
sam łuk i tak w sumie sześć razy. Punkty przecięcia łuków z wyjściowym
okręgiem wyznaczają wierzchołki sześciokąta foremnego.

Z

ADANIA

1

1. Przypomnij sobie konstrukcje trójkąta równobocznego i kwadratu.

1

2. Podaj konstrukcję okręgu stycznego do dwóch danych okręgów. Rozważ różne możliwości.

1

3. Skonstruuj trójkąt, mając dane trzy jego środkowe.

1

4. Przypomnij sobie konstrukcję odcinków o długościach równych iloczynowi lub ilorazowi dłu-

gości dwóch danych odcinków.

1

5. Dany jest okrąg bez środka. Skonstruuj jego środek. Ile sposobów możesz wskazać?

1

6. Skonstruuj romb, mając dane przekątną i wysokość.

1

7. Skonstruuj romb, mając dane wysokość i bok.

1

8. Skonstruuj równoległobok, mając dane dwie przekątne i bok.

1

9. Skonstruuj trapez ABCD, mając dane podstawę AB, wysokość oraz boki BC i AD.

10. Skonstruuj trójkąt ABC, mając dane kąty

α β

,

i dwusieczną kąta

α

.

11. Skonstruuj trójkąt ABC, mając dane

α

)

, dwusieczną CD oraz

CDA

)

.

Tu i w wielu innych zadaniach nie stosujemy formalnego rozróżnienia między kątem i jego
miarą. Podobnie postępujemy przy oznaczaniu odcinków; np. h

a

oznacza i wysokość, i jej

długość – w zależności od kontekstu i potrzeb. Wydaje się, że nie powinno dojść do nieporo-
zumień.