1

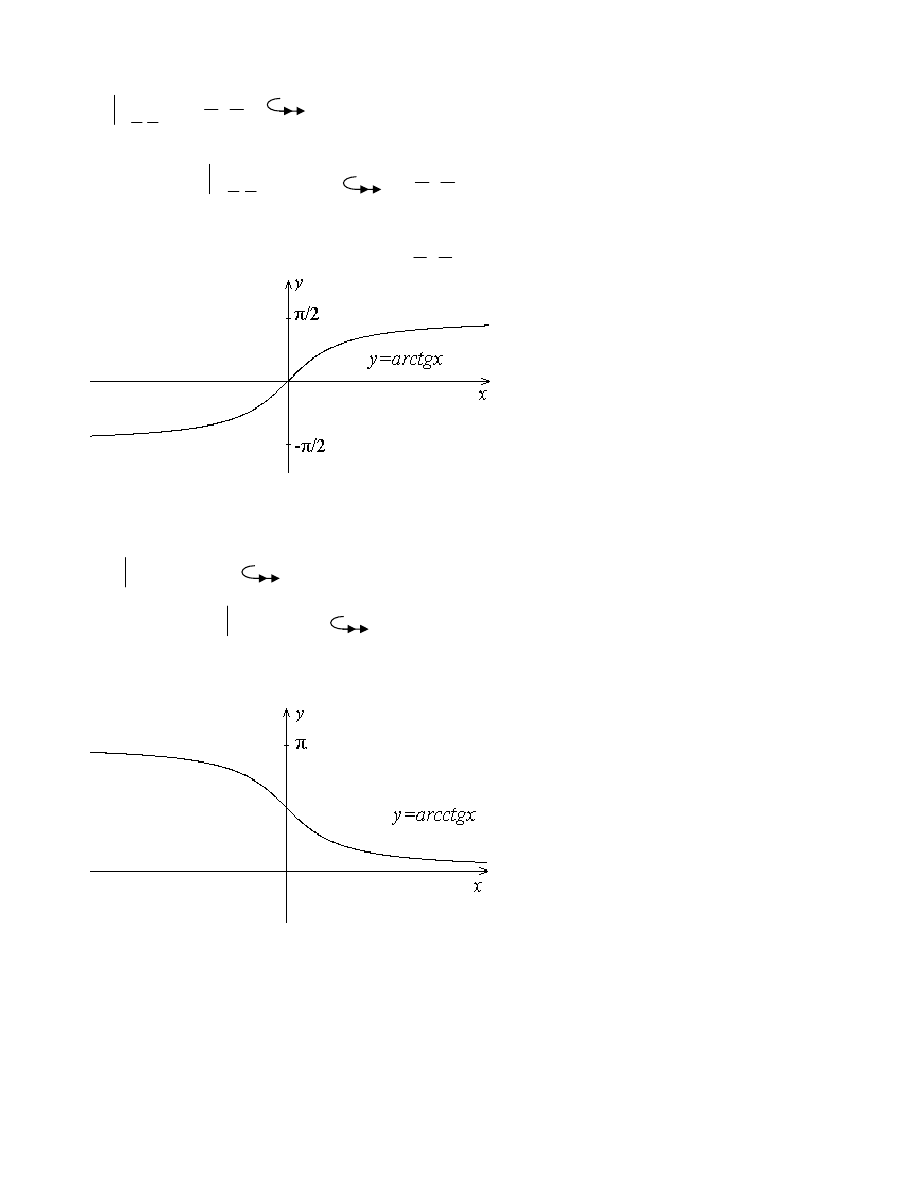
Funkcje cyklometryczne (funkcje odwrotne do pewnych restrykcji funkcji trygonometrycznych)

( )

(

)

2

2

,

,

:

2

2

π

π

π

π

−

−

tg

R

( )

R

tg

arctg

:

:

1

,

2

2

−

−

=

π

π

(

)

2

2

,

π

π

−

Niech

R

y

∈

. Wtedy:

( )

(

)

2

2

,

π

π

−

∈

∧

=

⇔

=

x

tgx

y

x

y

arctg

( )

( )

π

π

,

0

:

,

0

tg

c

R

( )

(

)

R

tg

c

arcctg

:

:

1

,

0

−

=

π

( )

π

,

0

Niech

R

y

∈

. Wtedy:

( )

( )

π

,

0

∈

∧

=

⇔

=

x

ctgx

y

x

y

arcctg

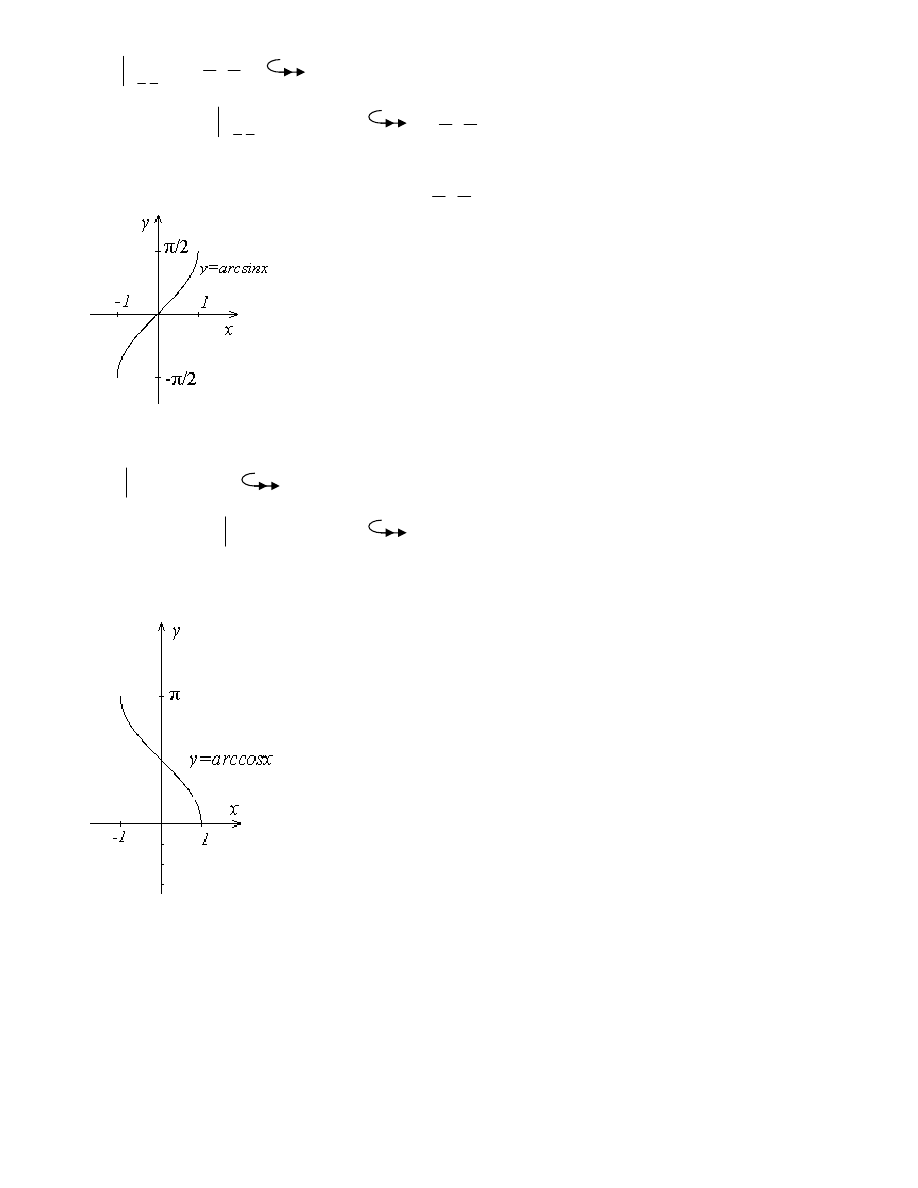
2

[ ]

[

]

2

2

,

,

:

sin

2

2

π

π

π

π

−

−

[ ]

1

,

1

−

[ ]

(

)

[ ]

1

,

1

:

sin

:

arcsin

1

,

2

2

−

=

−

−

π

π

[

]

2

2

,

π

π

−

Niech

[ ]

1

,

1

−

∈

y

. Wtedy:

( )

[

]

2

2

,

sin

arcsin

π

π

−

∈

∧

=

⇔

=

x

x

y

x

y

[ ]

[ ]

π

π

,

0

:

cos

,

0

[ ]

1

,

1

−

[ ]

(

)

[ ]

1

,

1

:

cos

:

arccos

1

,

0

−

=

−

π

[ ]

π

,

0

Niech

[ ]

1

,

1

−

∈

y

. Wtedy:

( )

[ ]

π

,

0

cos

arccos

∈

∧

=

⇔

=

x

x

y

x

y

3

Własno ci:

( )

x

tgx

arctg

=

, je li

(

)

2

2

,

π

π

−

∈

x

(

)

y

arctgy

tg

=

, je li

R

y

∈

( )

x

ctgx

arcctg

=

, je li

( )

π

,

0

∈

x

(

)

y

arcctgy

ctg

=

, je li

R

y

∈

(

)

x

x

=

sin

arcsin

, je li

[

]

2

2

,

π

π

−

∈

x

(

)

y

y

=

arcsin

sin

, je li

[ ]

1

,

1

−

∈

y

(

)

x

x

=

cos

arccos

, je li

[ ]

π

,

0

∈

x

(

)

y

y

=

arccos

cos

, je li

[ ]

1

,

1

−

∈

y