
Rozdzia÷10
Funkcje cyklometryczne
Witold Walas, Marek Ma÷olepszy
10.1.
Oblicz:
a)
arcsin
1
2
2 arccos
1
2
+ 3 arcctg 0;
b)
arccos
p
2
2
+ 3 arctg 1
2 arcsin
p
3
2
;
c)
arcsin
p
3
2
2 arccos
1
2
+arcctg
p
3 ;
d)
arcctg
p
3
3
+ arcsin
1
2
;
e)
arccos (0)
3 arctg ( 1) ;
f )
(2 + arctg 0) arcsin
p
2
2
;
g)
arcsin ( 1) + arccos
p
2
2
2
;
h)
1
arccos
p
3
2
2
arctg
p
3
3
;
i)
2
arcctg
p
3
3
3 arcsin
1
2
;
j)
(2 + arctg )
arcsin 0
;
k)
arctg
p
3
3
+ 2 arcctg ( 1) ;
l)
v
u
u
t
arctg
p
3
arccos
p
2
2
;
m)
s
3 arcctg ( 1)
arccos ( 1)
;
n)
arctg
p
3
3
arcctg 1
1
arcsin 1
;
o)
+ arccos 1
arctg
p
3 + arcctg
p
3
;
p)
arccos
p
3
2
arctg
p
3
1
:
10.2.
Oblicz:
a)
arccos cos
5
arctg tg
10
;
b)
arccos ( 1) 2 arcctg ( 1)+arctg
tg
5
;
c)
arcsin sin
3
arctg ctg
6
;
d)
sin arcsin
1
3
arctg
p
3
3
+ arccos 0;
e)
sin
2
(arctg 2) + cos
2
(arctg 2)
tg (arctg 2)
;
f )
arccos cos
2
7
arcsin sin
3
7
;
g)
jtg (arctg 3)
5j + ctg (arcctg ( 2)) ;
h)
2 arctg tg
5
3 arcctg ctg
8
;
i)
arcsin sin
1
2
+ arccos cos
5
4
1
;
j)
s
arcsin
sin
3
tg arctg
1
12
;
k)
arctg tg
1
4
cos arcsin
p
3
2
1
;
l)
arcsin cos
25
6
2 arctg ctg
11
4
:

2
Witold Walas, Marek Ma÷olepszy
10.3.
Oblicz:
a)
arctg tg
9
4
arcctg ctg
4
3
;
b)
arcsin sin
17
8
+ arccos cos
5
4
;
c)
arcsin cos
7
6
arccos cos
2
3
;
d)
arctg tg
10
7
+ arcctg ctg
18
7
;
e)
arcsin
sin
16
5
+ arccos cos
23
10
;
f )
arctg tg
85
11
arcctg ctg
126
11
;
g)
tg (arcctg 7) ;
h)
sin arccos
1
5
;
i)
arccos sin
9
5
;
j)
cos 2 arcsin
2
3
;
k)
arctg ctg
8
7
;
l)
arcctg tg
18
5
:
10.4.
Wyznacz zbiór warto´sci funkcji:
a)
f (x) =
+ 2 arcsin x;
b)
f (x) =
arccos (2x) ;
c)
f (x) =
4 arctg (x
1) ;
d)
f (x) =
2
arcctg x ;
e)
f (x) = 1 + 2
p
arccos x;
f )
f (x) = 2
2
arctg x
;
g)
f (x) = sin (arcctg (2x
1)) ;
h)
f (x) =
1
arcsin x
:
10.5.
Naszkicuj wykres funkcji:
a)
f (x) = 2 arcsin (x
1) ;
b)
f (x) = arccos jxj ;
c)
f (x) =
2
arccos x;
d)
f (x) = jarcsin (x + 1)j ;
e)
f (x) =
2 arctg x;
f )
f (x) =
1
2
arcctg (x
3) ;
g)
f (x) =
arctg x +
2
;
h)
f (x) =
jarctg xj ;
i)
f (x) = arcsin (2x + 1) +
2
;
j)
f (x) = 2 arccos
1
2
x
3
2
:
10.6.
Naszkicuj wykres funkcji:
a)
f (x) = arccos x
arcsin x;
b)
f (x) = arcsin x + arccos
1
x
;
c)
f (x) = sin (arcsin x) ;
d)
f (x) = arcsin (sin x) ; x 2
2
;
2
;
e)
f (x) = arcsin (cos x) ; x 2 [
; ] ;
f )
f (x) = cos(arcsin x);
g)
f (x) = ctg (arcctg (x
2)) ;
h)
f (x) = arctg (tg x) :
10.7.
Zbadaj parzysto´s´c (nieparzysto´s´c) funkcji:
a)
f (x) = jxj arcsin x;
b)
f (x) = x
3
arctg x;
c)
f (x) = x + arcsin
1
x
;
d)
f (x) = x
2
arccos x;
e)
f (x) = arcctg x
arcctg ( x) ;
f )
f (x) = (cos x + 1) arcsin (x
1) ;
g)
f (x) =
1
1 x
2
arccos jxj ;
h)
f (x) = sin x arcctg x;
i)
f (x) = cos (arcsin x) :
10.8.
Rozwi ¾
a·
z równanie:
a)
arcsin (x
2) =
4
;
b)
arctg(1
2x) =
4
;
c)
arccos ( 2x + 3) =
3
;
d)
arcctg (5x
2) =
6
;
10. Funkcje cyklometryczne
3
e)
arcsin 2
p
3x =
3
;
f )
arccos
x+1
3
=
5
6
;
g)
2 arcctg
1
3
x
1 =
4
3
;
h)
arctg (2x + 3) =
arctg 5;
i)
arccos (2
x)
2
= arcsin
p
3
2
;
j)
arcsin (3x
2) =
arccos
1
2
;
k)
arctg j2
xj = ;
l)
arcctg
1
3
x + 2 =
2
3
:
10.9.
Rozwi ¾
a·
z równanie:
a)
arcctg jxj =
3
;
b)
arcsin j2x
1j =
6
;
c)
2
+ arccos x =
3
;
d)
arctg
1
x
=
6
;
e)
arctg 6x
2
= arctg (5x + 6) ;
f )
arcctg x
2
2x
2 =
4
;
g)
arcsin x
2
x
1 = arccos 0;
h)
arccos(3x
2
+
1
2
x) =
3
;
i)
arccos
x
2
1
x+3
=
2
;
j)
arcsin
x
x 1
=
6
;
k)
arctg
2
x
2
1
=
4
;
l)
arcctg
2
p
3x
x+1
=
5
6
:
10.10.
Rozwi ¾
a·
z równanie:
a)
arcctg
2
x =
2
arcctg x;
b)
16
2
arctg
2
x = 1;
c)
4 arccos
2
x
4 arccos x +
3
4
2
= 0;
d)
3 arcsin
2
x
2 arcsin x =
2
;
e)
arcsin x
arcsin x
6
=
1
2
;
f )
arccos x
arccos x
2
=
2;
g)
arctg x =
arctg x
2 + arctg x
;
h)
2 arccos x
3 arccos x
+ 3 arccos x
= 0;
i)
ctg (2 arctg x) =
p
3
3
;
j)
sin (4 arcctg x) = 1;
k)
arcctg x = arctg x;
l)
arccos x + arccos 2x =
2
:
10.11.
Rozwi ¾
a·
z nierówno´s´c:
a)
arccos (2x
1) >
3
;
b)
2 arcsin (2
3x)
6
3
;
c)
1
2
arcsin x
2
>
4
;
d)
arctg (x + 1)
>
4
;
e)
2 arcctg (1
x) +
<
5
2
;
f )
arccos
1
2
x < arccos (x + 1) ;
g)
arctg (x
1)
> + arcctg (x + 1) ;
h)
arcsin
1
2
x + 1 < arcsin (2 + x) ;
i)
arcctg (4
3x) < arctg 1;
j)
arctg (2x
1)
> arcctg
p
3
3
:
10.12.
Rozwi ¾
a·
z nierówno´s´c:
a)
jarcsin (x
1)j 6
3
;
b)
arccos jxj <
4
;
c)
arctg j2x + 1j > arctg 3;
d)
2
arcctg x <
6
;
e)
arctg 2x
2
x <
4
;
f )
arcctg x
2
6 < arcctg x;
g)
arcctg 2x
2
> arcctg (3
x) ;
h)
arcsin x
2
1
2
x >
6
;
i)
2
arcsin x
<
6
;
j)
arcsin
1
2
x
6 arccos (x 1)
2
:
4
Witold Walas, Marek Ma÷olepszy
10.13.
Wyznacz dziedzin ¾
e funkcji:
a)
f (x) = arcsin (2x
1) ;
b)
f (x) = arccos x
2
+ x
1 ;
c)
f (x) = arccos (2 sin x) ;
d)
f (x) =
q
2
arctg (x
1)
1
2
;
e)
f (x) = arccos
p
x
2
4x + 4;
f )
f (x) = arctg
2
arcsin
1
3
x + 1
1
;
g)
f (x) = arcsin
x 1
3x+2
;
h)
f (x) =
p
arctg (arcsin (1
x
2
));
i)
f (x) = arcsin
x
p
x
2
+1
;
j)
f (x) =
p
arcctg (arcsin (x
2
4x + 3));
k)
f (x) =
1
q
3
arcsin 2x
1
2
;
l)
f (x) =
q
4
arcctg
2x
x+1
1
:
Odpowiedzi
10.1.
a)
b)
5
6
c)
11
6
d)
2
e)
5
4
f )
2
g)
2
16
h)
18
i)
1
3
j)
1
k)
5
3
l)
2
3
m)
3
2
n)
p
6
3
o)
6
p)
2
10.2.
a)
10
b)
7
10
c)
0
d)
+1
3
e)
1
2
f )
2
3
g)
0
h)
40
i)
4
3
j)
2
p
k)
4
l)
5
6
10.3.
a)
12
b)
7
8
c)
d)
e)
2
f )
3
5
g)
1
7
h)
2
p
6
5
i)
7
10
j)
1
9
k)
5
14
l)
9
10
10.4.
a)
[ 2 ; 0]
b)
[0; ]
c)
( 2 ; 2 )
d)
[0;
2
)
e)
[1; 1 + 2
p
]
f )
1
2
; 2
g)
(0; 1]
h)
( 1;
2
] [ [
2
; +1)
10.5.
a)
x
y
1 2
π/2
π
−π/2
−π
b)
x
y
1
−1
π/2
−π/2
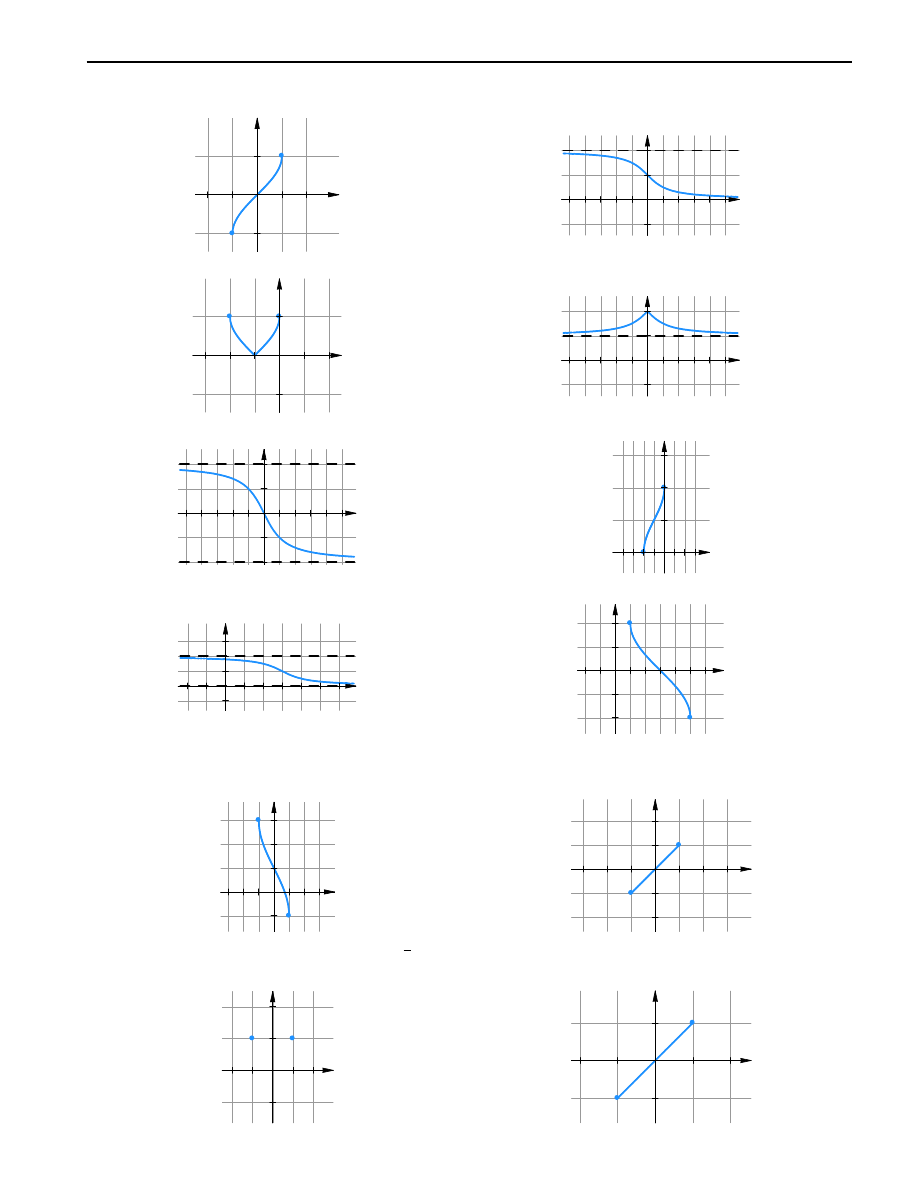
10. Funkcje cyklometryczne
5
c)
x
y
1
−1
π/2
−π/2
d)
x
y
1
−1
−2
π/2
−π/2
e)
x
y
1
−1
π/2
π
−π/2
−π
f )
x
y
1
3
π/2
π/4
−π/4
3π/4
g)
x
y
1
−1
π/2
π
−π/2
h)
x
y
1
−1
π/2
π
−π/2
i)
x
y
1
−1
π/2
π
j)
x
y
1
3
5
π/2
π
−π/2
−π
10.6.
a)
x
y
1
−1
π/2
π
3π/2
−π/2
wskazówka: arcsin x + arccos x =
2
b)
x
y
1
−1
π/2
π
−π/2
c)
x
y
1
−1
1
−1
d)
x
y
π/2
π
−π/2
−π
π/2
−π/2
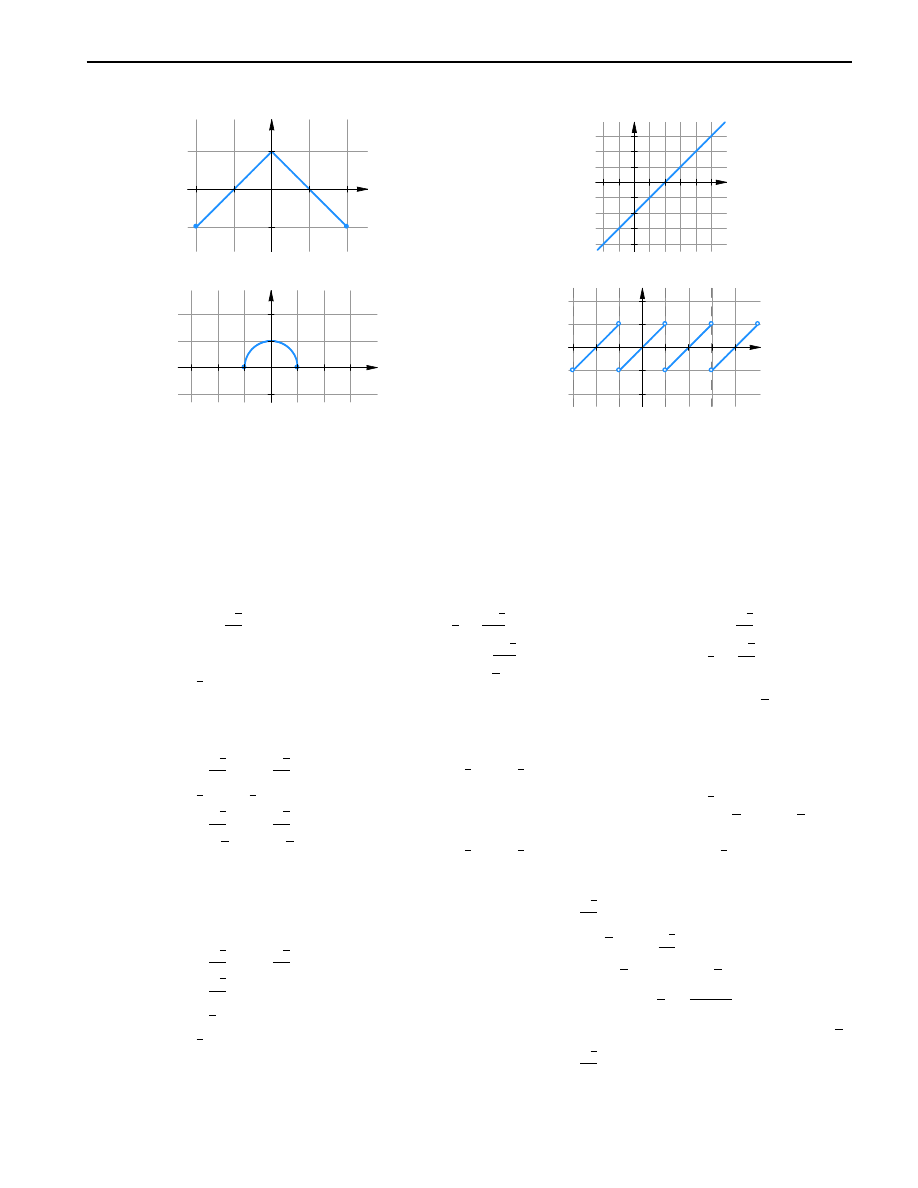
6
Witold Walas, Marek Ma÷olepszy
e)
x
y
π/2
π
−π/2
−π
π/2
−π/2
f )
x
y
1
−1
1
−1
g)
x
y
1 2
1
−1
h)
x
y
π/2
π
3π/2 2π
−π/2
−π
−3π /2
π/2
π
−π/2
−π
10.7.
a)
nieparzysta;
b)
parzysta;
c)
nieparzysta;
d)
nie jest parzysta ani nieparzysta;
e)
nieparzysta;
f )
nie jest parzysta ani nieparzysta;
g)
parzysta;
h)
nie jest parzysta ani nieparzysta;
i)
parzysta.
10.8.
a)
x = 2 +
p
2
2
b)
x = 1
c)
x =
5
4
d)
brak pierwiastków
e)
x =
1
2
+
2
p
3
3
f )
x =
1
3
p
3
2
g)
x = 3
p
3
h)
x =
4
i)
x = 2 +
p
3
2
j)
x =
2
3
p
3
6
k)
brak pierwiastków
l)
x =
6
p
3
10.9.
a)
x =
p
3
3
; x =
p
3
3
b)
x =
1
4
; x =
3
4
c)
x =
p
3
2
; x =
p
3
2
d)
x =
p
3; x =
p
3
e)
x =
2
3
; x =
3
2
f )
x =
1; x = 3
g)
x =
1; x = 2
h)
x =
1
2
; x =
1
3
i)
x =
1; x = 1
j)
x =
1
3
k)
x =
p
3; x =
p
3
l)
x =
1
3
10.10.
a)
x = 0
b)
x =
1; x = 1
c)
x =
p
2
2
; x =
p
2
2
d)
x =
p
3
2
e)
x =
1
2
f )
x =
1
2
g)
x = 0; x =
tg 1
h)
x =
p
3
2
; x = 1
i)
x =
p
3; x =
p
3
3
j)
x = 1
p
2; x = 1 +
p
2;
wskazówka: tg
x
2
=
sin x
1+cos x
, cos x 6= 1
k)
x = 1; wskazówka: arctg x + arcctg x =
2
l)
x =
p
5
5
10.11.
10. Funkcje cyklometryczne
7
a)
x 2 [0;
3
4
)
b)
x 2
5
6
; 1
c)
brak rozwi ¾
aza´n
d)
x 2 [ 2; +1)
e)
x 2 ( 1; 2)
f )
x 2
1
2
;
1
4
g)
brak rozwi ¾
aza´n
h)
x 2 ( 2; 1]
i)
x 2 ( 1; 1)
j)
x 2
h
p
3+1
2
; +1
10.12.
a)
x 2
h
1
p
3
2
; 1 +
p
3
2
i
b)
x 2
h
1;
p
2
2
[
p
2
2
; 1
i
c)
x 2 ( 1; 2) [ (1; +1)
d)
x 2
p
3
3
;
p
3
3
e)
x 2
1
2
; 1
f )
x 2 ( 1; 2) [ (3; +1)
g)
x 2
3
2
; 1
h)
x 2
h
1
p
17
4
;
1
2
[ 1;
1+
p
17
4
i
i)
x 2 [ 1; 0) [ (
p
3
2
; 1]
j)
x 2 0;
2
3
;
wskazówka: arcsin x + arccos x =
2
10.13.
a)
x 2 [0; 1]
b)
x 2 [ 2; 1] [ [0; 1]
c)
x 2
6
+ k ;
6
+ k
; k 2 Z
d)
x 2 [2; +1)
e)
x 2 [1; 3]
f )
x 2 [ 6; 0)
g)
x 2 ( 1;
3
2
] [ [
1
4
; +1)
h)
x 2
p
2;
1 [ 1;
p
2
i)
x 2 R
j)
x 2 2
p
2; 2 +
p
2
k)
x 2
1
p
3
4
;
1+
p
3
4
l)
x 2 ( 1; 1) [ (1; +1)
Wyszukiwarka
Podobne podstrony:
C1a[1]. Funkcje cyklometryczne
Funkcje cyklometryczne 3
funkcje cyklometryczne
lista funkcje cyklometryczne
wykład, Funkcje cyklometryczne wykład dodatkowy, Funkcje cyklometryczne
Funkcje cyklometryczne 2
funkcje cyklometryczne
2 Funkcje cyklometryczne (2)
Funkcje cyklometryczne
Funkcje cyklometryczne, Geodezja, studia III rok
Ca│ki funkcji cyklometrycznych
Funkcje cyklometryczne 2
Całki funkcji cyklometrycznych
więcej podobnych podstron