1

Pomiar momentu obrotowego użytecznego silnika torsjometrem

Wstęp

Doświadczalne wyznaczenie sprawności energetycznej układu napędowego silników nie
badanych na stanowisku próbnym sprawia na ogół wiele kłopotów ze względu na trudność
zmierzenia w warunkach roboczych mocy efektywnej oddawanej na wał przez układ
napędowy. Szybki rozwój techniki pomiarowej przyniósł jednak jeszcze w okresie przed
drugą wojną światową szereg przyrządów, których prototypy sięgają roku 1900,
umożliwiających pomiar mocy efektywnej na wale bez potrzeby rozmontowania wału czy też
przenoszenia silnika na stanowisko próbne. Stało się to możliwe dzięki zastosowaniu w
przyrządach pomiarowych czujników i układów lamp elektronowych, dających bardzo duże
wzmocnienie wielkości mierzonych.
Przykład pomiarów torsjometrycznych jest jeszcze jednym dowodem jak wielką pomocą
mogą się stać z odpowiednio zastosowane układy wzmacniakowe do pomiarów wielkości
mechanicznych. Prawie wszystkie nowoczesne torsjometry wykorzystują do pomiaru mocy
efektywnej odkształcenie wału wynikłe z działania momentu skręcającego. Odkształcenie to
jest niezmiernie małe i wyraża się liczbą rzędu 0,05° na 1 m długości wału, przy obciążeniu
nominalnym. Wielkość ta charakteryzuje trudności, z jakimi spotyka się konstruktor
przyrządu. Dokładne zmierzenie takiej wielkości przy jednoczesnym zachowaniu zasady
ekonomiczności przyrządu i możliwie łatwych warunków eksploatacji jest prawie niemożliwe
bez układów wzmacniakowych i odpowiednich czujników mechaniczno-elektrycznych. Tą
drogą poszły też wysiłki konstruktorów w wyniku czego opracowano kilka torsjometrów, z
których najczęściej używane są: torsjometr Siemens-Forda oparty na zasadzie indukcyjnej
oraz torsjometr Maihaka — akustyczny.
Zasada pomiaru w obu torsjometrach jest zbliżona, jakkolwiek zastosowano w nich różne
czujniki. Polega ona na porównaniu przyrostu nieznanego, mierzonego odkształcenia wału ze
znanym, dokładnie wycechowanym przyrostem odkształcenia identycznego układu
pomiarowego umieszczonego w przyrządzie. Porównanie to przez zastosowanie indykatorów
elektrycznych, jak np. lampy oscylograficznej, może być dokonana praktycznie bezbłędnie.
W wypadku odkształcenia wału wielkość mierzona jest transformowana w zmiany wielkości
elektrycznej, np. w zmiany częstotliwości — jak to jest w torsjometrze Maihaka — lub w
zmiany indukcyjności — w torsjometrze Siemens—Forda. Elementem przetwarzającym jest
czujnik mechaniczno-elektryczny, w którym wyjściowa wielkość elektryczna jest ściśle
związana z wejściową wielkością nieelektryczną, np. kątem skręcenia wału. Zależność ta jest
dokładnie znana.
W zerowej metodzie porównania, jaka jest stosowana w wyżej wymienionych torsjometrach,
wpływ części elektrycznej na dokładność pomiaru jest praktycznie pomijalny. Według
literatury fachowej błąd pomiaru torsjometru Maihaka i Siemens—Forda wynosi, 2% co dla
tego rodzaju przyrządów stanowi bardzo dużą dokładność.

Podstawy teoretyczne pomiaru mocy na wale

Zależności mechaniczne

Wał śrubowy obciążony momentem M

s

, ulega w czasie pracy skręceniu o kąt

φ Kat ten jcsi

proporcjonalny do długości bazy pomiarowej l, to znaczy do długości odcinka wału, na
którym mierzone jest skręcenie (rys.1).

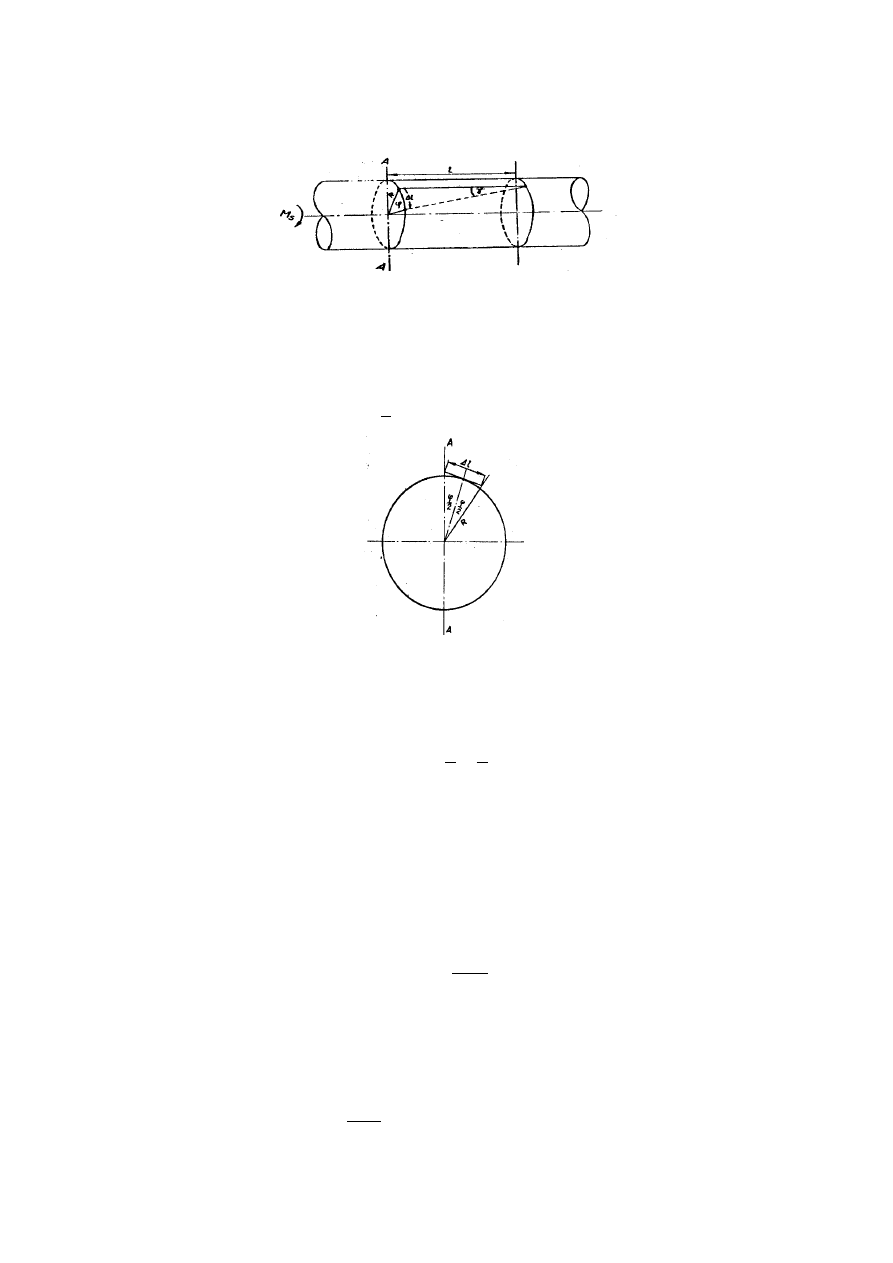
2

Rys. 1. Skręcenie wału pod wpływem działania momentu M

s

Na rys. 2 pokazany jest przekrój A-A wału, z którego widać, że:

2

tg

R

2

l

φ

⋅

=

∆

(1)

Rys. 2. Przekrój wału skręcanego

Dla małych kątów

φ można przyjąć:

2

2

tg

φ

≅

φ

(2)

Uwzględniając (2) w równaniu (1) otrzymujemy:

φ

⋅

≅

∆

R

l

(3)

Z teorii wytrzymałości wiemy, że kąt skręcenia wału obciążonego momentem skręcającym
M

s

mierzony na odcinku l wynosi:

o

s

I

G

l

M

⋅

⋅

=

φ

(4)

gdzie:

G - moduł odkształcenia postaciowego (kN/m

2

),wynoszący dla stali 8.14

⋅10

7

[kN/m

2

],

I

o

- biegunowy moment bezwładności przekroju wału (m

4

):

Dla wału pełnego;

32

D

I

4

o

⋅

π

=

(5)

3

D – średnica zewnętrzna wału (m),
M

s

– moment skręcający (Nm),

l – baza pomiarowa (l).

Podstawiając obliczoną wartość

φ do równania (3) oraz rozwiązując je względem M

s

otrzymujemy:

l

R

I

G

l

M

o

s

⋅

⋅

⋅

∆

=

(6)

Moc silnika (W), przenoszona przez wał skręcany momentem M

s

i obracający się z

prędkością obrotową n (obr/min), jest:

30

n

M

M

P

s

s

e

⋅

π

⋅

=

ω

⋅

=

(7)

Uwzględniając powyższe równania otrzymujemy ostatecznie wyrażenie na moc przenoszona
przez wał jako funkcję odkształcenia

∆l mierzonego na odcinku wału l:

30

n

l

R

I

G

l

P

o

e

⋅

π

⋅

⋅

⋅

⋅

∆

=

(8)

Dla danego wału wielkości: G, I

o

, R, l, są stałe i można je zastąpić przez współczynnik K:

30

l

R

I

G

K

o

π

⋅

⋅

⋅

=

(9)

Otrzymamy ostatecznie wzór na moc przenoszona przez wał, w funkcji odkształcenia wału

∆l

i prędkości obrotowej n:

n

K

l

P

e

⋅

⋅

∆

=

(10)

Dane do obliczeń:

1. długość pomiarowa: l = 80 mm = 0.08m,
2. odległość strun pomiarowych od osi symetrii wału: R = 108.1 mm = 0.1081 m,
3. stała struny (nr. 18700): C

1

= 3.87

⋅10

-5

cm/działka = 3.87

⋅10

-7

m/działka,

4. stała struny (nr. 23381): C

2

= 4.02

⋅10

-5

cm/działka = 4.02

⋅10

-7

m/działka,

5. średnica wału: D = 145 mm = 0.145 m,
6. moduł sprężystości wały: G = 8.14

⋅10

7

kNm/m

2

.

Objaśnienia uzupełniające:

∆l – wydłużenie lub skrócenie struny struny,

∆l

1

=C

1

(z

1

-z

01

) = C

1

⋅∆z

1

∆l

2

=C

2

(z

02

-z

2

) = C

2

⋅∆z

2

2

z

C

z

C

l

2

2

1

1

śr

∆

⋅

+

∆

⋅

=

∆

z

01

, z

02

– wyniki zerowania strun 1 i 2,

z

1

, z

2

– wyniki odczytane dla strun 1 i 2 w czasie pomiaru momentu obrotowego (pod

obciążeniem).

4

Obliczenia:

1. Stała K

32

D

I

4

o

⋅

π

=

32

145

.

0

14

.

3

I

4

o

⋅

=

30

l

R

I

G

K

o

π

⋅

⋅

⋅

=

44

.

42658

25944

.

0

10

67306

.

110

30

08

.

0

1081

.

0

14

.

3

10

33

.

4

10

14

.

8

K

2

5

7

=

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

=

−

2. Odkształcenie wału ∆l

śr

2

z

C

z

C

l

2

2

1

1

śr

∆

⋅

+

∆

⋅

=

∆

(

) (

)

[

]

2

7

1

7

sr

z

10

87

.

3

z

10

02

.

4

5

.

0

l

∆

⋅

⋅

+

∆

⋅

⋅

=

∆

−

−

3. Moc użyteczna P

e

(

) (

)

[

]

n

z

87

.

3

z

02

.

4

10

22

.

21329

n

K

l

P

2

1

7

śr

e

⋅

∆

⋅

+

∆

⋅

⋅

=

⋅

⋅

∆

=

(

) (

)

[

]

n

z

87

.

3

z

02

.

4

10

132922

.

2

P

2

1

3

e

⋅

∆

⋅

+

∆

⋅

⋅

=

[kW]

Układy pomiaru zużycia paliwa

Wprowadzenie

Ilość paliwa zużytego przez silnik przypadająca na jednostkę wytworzonej pracy lub też na
jednostkę drogi przebytej przez pojazd jest miarą jego sprawności. W badaniach silników
ilość zużytego paliwa określa się w postaci dwóch wielkości:

• Godzinowego,

• Jednostkowego zużycia paliwa.

Godzinowe (lub sekundowe) zużycie paliwa B w kg/h (lub g/s) określa masę paliwa zużytego
przez silnik w jednostce czasu i wyraża się zależnością:

t

V

B

p

p

ρ

⋅

=

lub

t

m

B

=

gdzie:
V

p

- objętość paliwa zużytego w czasie pomiaru, m

3

,

ρ

p

- gęstość paliwa w warunkach pomiaru, kg/m

3

,

t - czas zużycia paliwa podczas pomiaru, s,
m - masa paliwa zużytego podczas pomiarów, kg.

Jednostkowe zużycie paliwa b (g/kWh) określa ilość paliwa zużytego przez silnik
przypadającą na jednostkę mocy:

5

e

P

B

b

=

gdzie:
P

e

- jest mocą użyteczną silnika wyrażoną w kW.

Pomiar godzinowego zużycia paliwa nie nastręcza większych trudności, natomiast w celu
wyznaczenia jednostkowego zużycia paliwa należy wykonać pomiary następujących
wielkości: prędkości obrotowej wału korbowego, momentu obrotowego silnika, masy
zużytego paliwa oraz czasu, w jakim dokonywano pomiaru.

Metody pomiaru zużycia paliwa

Do pomiaru zużycia paliwa najczęściej wykorzystuje się metody objętościową i wagową.
Najprostszą metodą pomiaru zużycia paliwa przez silnik zarówno podczas pomiarów
eksploatacyjnych, jak i podczas badań silnika na hamowni, jest metoda objętościowa. Pomiar
średniego objętościowego zużycia paliwa wykonuje się za pomocą zbiornika pomiarowego.
Naczynie pomiarowe połączone jest z układem zasilania silnika za pomocą trójdrożnego
zaworu, który pozwala na pracę w trzech położeniach:

• zasilanie ze zbiornika pomiarowego,
• zasilanie ze zbiornika głównego,

• zasilanie połączone z napełnianiem zbiornika pomiarowego.

Czas zużycia określonej objętości paliwa wyznacza się, mierząc czas obniżania się poziomu
paliwa od górnej do dolnej kreski zaznaczonej na zbiorniku pomiarowym. Masę paliwa
określa iloczyn objętości i gęstości paliwa w czasie pomiaru.
Pomiar zużycia paliwa metodą objętościową obarczony jest błędem tym większym, im
mniejsza jest dokładność wyznaczania objętości zużytego paliwa i czasu pomiaru. Wadą
metody objętościowej jest również konieczność uwzględnienia zmian gęstości paliwa w
czasie pomiarów.
W czasie badań silnika należy pamiętać o tym, aby po zakończeniu pomiaru zużycia paliwa z
wykorzystaniem naczynia pomiarowego przedstawionego przełączyć zawór trójdrożny do
pozycji zapewniającej zasilanie silnika ze zbiornika głównego. Jest to szczególnie ważne w
przypadku silników z zapłonem samoczynnym. gdyż nieodpowiednio prowadzony pomiar
może spowodować zapowietrzenie układu paliwowego.

Wyznaczanie gęstości produktów naftowych

Rozróżnia się dwa określenia gęstości ciał (masy właściwej):

• gęstość bezwzględna – gęstością bezwzględną p danego ciała nazywamy stosunek

masy m do objętości V, wyznaczonych w tej samej temperaturze:

6

• gęstość względna - gęstością względną d

tr

nazywamy stosunek gęstości badanego ciała

w temperaturze odniesienia t do gęstości innej substancji w temperaturze odniesienia
t

r

, np. do gęstości wody w temperaturze 4°C, wyrażoną wzorem:

Jeżeli objętości obu substancji są równe (V = V

w

), to:

Temperatura odniesienia to temperatura, w której należy oznaczyć lub, do której należy
odnieść gęstość badanej substancji w innej temperaturze. Zgodnie z normą temperaturą
odniesienia dla gęstości jest 15°C. Jeśli pomiar gęstości jest wykonywany w innej
temperaturze, należy przeliczyć gęstość w temperaturze; oznaczania na gęstość w
temperaturze 15°C. W tym celu należy posłużyć się tablicą, która zawiera przeliczenia
gęstości produktów naftowych w temperaturze oznaczania (t) na gęstość w temperaturze
odniesienia (t = 15°C).
Przy wyznaczaniu gęstości ciał stałych jako ciało wzorcowe przyjmuje się wodę destylowaną,
której gęstość w temperaturze 20°C jest równa 1000 kg/m

3

.

Masa ciała jest wielkością stałą, natomiast ciężar ciała jest zmienny i zależy np. od szerokości
geograficznej położenia ciała. Jeżeli objętość ciała nie zmienia się, to gęstość jest wielkością
stałą, a ciężar właściwy jest zmienny i zmienia się wraz z ciężarem ciała. Ciężar właściwy ma
wartość liczbowo równą gęstości danego ciała w średnich szerokościach geograficznych
(zmienia się tylko jednostka).
Przy wyznaczaniu gęstości paliw silnikowych należy mieć na uwadze, że pod względem
chemicznym nie są one ciałami jednorodnymi, ale stanowią mieszaniny różnych związków.
Najliczniejszą grupę stanowią węglowodory. których gęstość zawiera się w szerokim zakresie
od 621 kg/m

3

dla izopentanu (C

5

H

12

) do 884 kg/m

3

dla benzenu (C

6

H

6

). Stosunkowo

niewielką grupę stanowią takie związki, jak siarka, żywice, kwasy i zasady rozpuszczalne w
wodzie, a także sama woda.
W skład paliw wchodzą różne związki, gęstość paliwa należy więc rozumieć jako gęstość
mieszaniny tych związków. Znając gęstość paliwa, można zaszeregować je do napędu
określonej grupy silników spalinowych. Silniki o zapłonie iskrowym zasilane są paliwem o
mniejszej gęstości, a silniki o zapłonie samoczynnym - paliwem o większej gęstości.
Zestawienie gęstości paliw w zależności od przeznaczenia silnika przedstawiono w tablicy.

7

Tablica

Gęstość paliw stosowanych w silnikach spalinowych

Rodzaj paliwa

silnikowego

Gęstość w temp.

20°C,

kg/m

3

Zastosowanie w silnikach spalinowych

Benzyna

700

÷785

z zapłonem iskrowym

Nafta

760

÷860

z zapłonem iskrowym i z urządzeniami podgrzewającymi

paliwo

Olej napędowy

830

÷920

z zapłonem samoczynnym - trakcyjne

Olej opałowy

890

÷950

z zapłonem samoczynnym - okrętowe

Do pomiaru gęstości paliw płynnych i olejów silnikowych stosowanych w silnikach
spalinowych używa się najczęściej areometru, wagi hydrostatycznej lub piknometru.
Znajomość prawa Pascala oraz prawa Archimedesa pozwala wyznaczyć gęstość cieczy za
pomocą areometru i wagi hydrostatycznej, a umiejętność ważenia jest przydatna do pomiaru
gęstości za pomocą piknometru.
Metoda oznaczania gęstości areometrem
Metodę tę stosuje się do oznaczania gęstości produktów naftowych, które w normalnych
warunkach są cieczami i których prężność par jest nie większa niż 180 kPa (wg PN-84/C-
04036).
Areometr

to wąska rurka szklana zakończona kulistym zbiornikiem wypełnionym śrutem lub

rtęcią. Często w jego wnętrzu umieszcza się termometr i wtedy mamy do czynienia z
termoareometrem. Górna część areometru jest wyskalowana tak, że można odczytywać
wyniki z dokładnością do czwartego miejsca znaczącego. Areometr zanurzony w cieczy
pływa w pozycji pionowej. Każda inna pozycja wskazuje na jego uszkodzenie.
Przebieg pomiarów i przyrządy:

1. Zestaw areometrów szklanych z podziałką elementarną 0.001 g/ml i z podziałką

cząstkową 0.050 g/ml.

2. Cylinder mierniczy z bezbarwnego szkła o średnicy wewnętrznej co najmniej 0.25

mrn większej od zewnętrznej średnicy stosowanego areometru. Wysokość cylindra
powinna być taka, aby dolny koniec areometru znajdował się co najmniej 25 mm od
dna cylindra.

3. Zestaw termometrów o zakresie pomiarowym od -15°C do 102°C z podziałką

elementarną 0.5°C.

Przygotowanie przyrządów, pomiar:

Przed wykonaniem pomiarów przyrządy przemyć benzyną (ekstrakcyjną) lub

eterem naftowym i osuszyć.

Do cylindra mierniczego wlać badany produkt, tak aby nie utworzyły się

pęcherzyki powietrza.

Zmierzyć temperaturę badanego produktu.

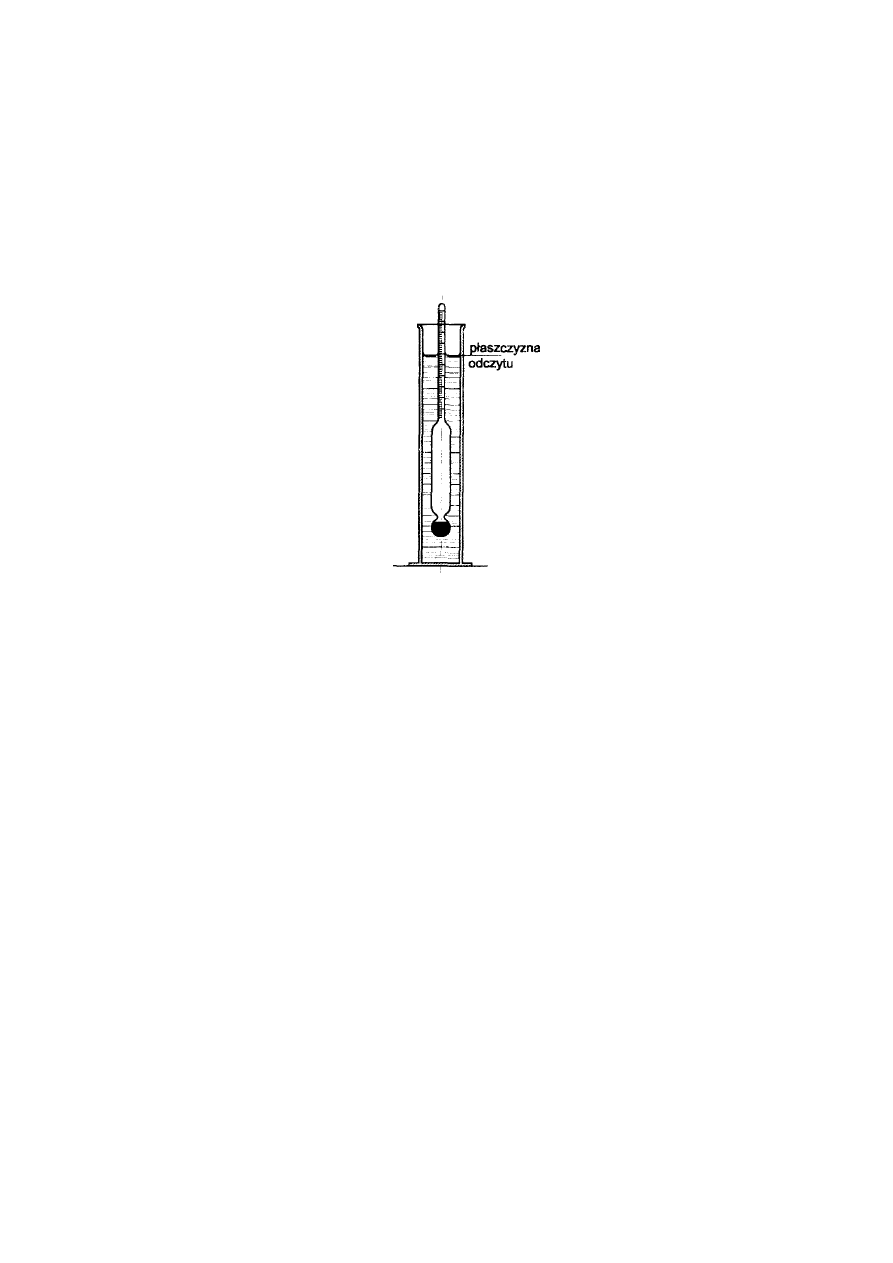
8

Areometr zanurzyć ostrożnie w badanej cieczy, tak aby nie nastąpiło uderzenie

o dno naczynia (co mogłoby spowodować zniszczenie areometru). Areometr lekko
nacisnąć, aby zanurzył się mniej więcej na 2 działki skali, po czym pozwolić mu na
swobodne ustalenie położenia (ważne w przypadku produktów o dużej lepkości).
Odczytać wartość gęstości z podziałki areometru z dokładnością do najbliższej
działki elementarnej według menisku górnego.

Rys. Odczytywanie wskazań areometru

Zmierzyć ponownie temperaturę badanego produktu. Za temperaturę

oznaczenia (tr) przyjąć średnią wartość temperatury przed odczytaniem gęstości i po
odczycie, przy czyn różnica między nimi nie może być większa niż 0.5°C. Jeśli
różnica przekracza tę wartość, cały pomiar należy powtórzyć. Jeśli pomiar był
wykonany w temperaturze innej niż 15°C, należy wynik pomiarów sprowadzić do
warunków standardowych, tj. do temperatury 15°C.

Wyniki pomiarów wykonywane w tych samych warunkach i tym samym

przyrządem należy uznać za prawidłowe, jeśli nie różnią się między sobą więcej niż
o 0.001 g/ml. Wyniki pomiaru należy zawsze podawać wraz z temperaturą.