Ćwiczenie 6
Pomiary wielkości elektrycznych za pomocą oscyloskopu
6.1. Cel ćwiczenia
Zapoznanie z budową, zasadą działa oscyloskopu oraz oscyloskopowymi metodami
pomiarowymi. Wykonanie pomiarów wielkości elektrycznych (okresu, wartości maksymalnej
i międzyszczytowej, przesunięcia fazowego, częstotliwości) za pomocą oscyloskopu.
6.2. Pomiar czułości wejść X i Y badanego oscyloskopu
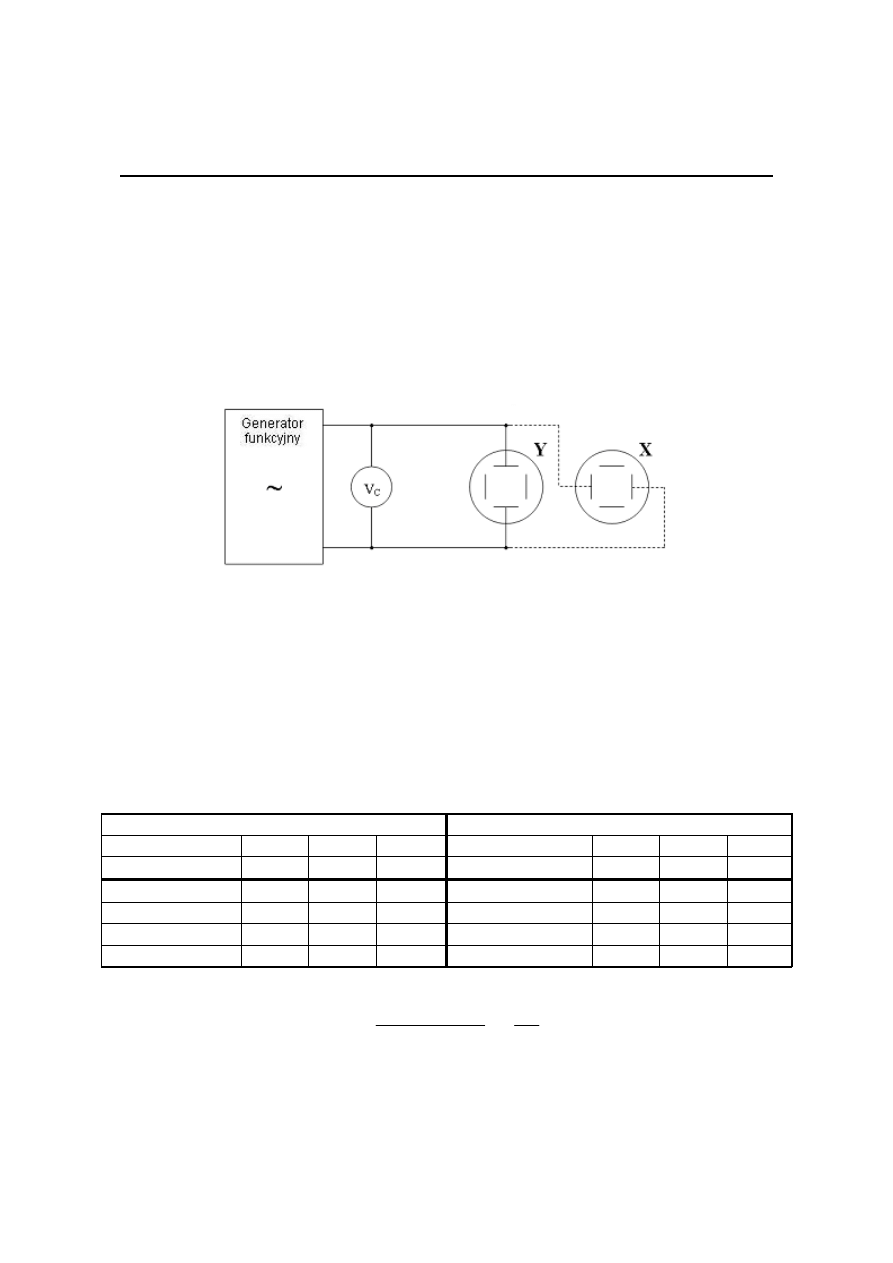
6.2.1. Schemat układu pomiarowego
UWAGA!
Pomiary należy wykonać w położeniu 1 V/div (1 V/cm) przełącznika obwodu
wejściowego X i Y. W tym celu należy wyłączyć podstawę czasu (pokrętło regulacji
podstawy czasu skręcić maksymalnie w prawą stronę) i zmieniając wartość napięcia
podawanego z generatora na wejście oscyloskopu, mierzyć długość linii na ekranie. Wyniki
zanotować w tabeli.
6.2.2. Tabela pomiarowa
Wejście X
Wejście Y
Długość linii
U
v
U
m
S
x
Długość linii
U
v
U
m
S
y
div
V V
div/V
div
V V
div/V
10
8
8
6
6
4
4
2
⎥⎦
⎤
⎢⎣
⎡
⋅
=
V
div
U
linii
dlugosc
S
m
2
1
6.3. Obserwacja i odwzorowanie różnych przebiegów okresowo zmiennych
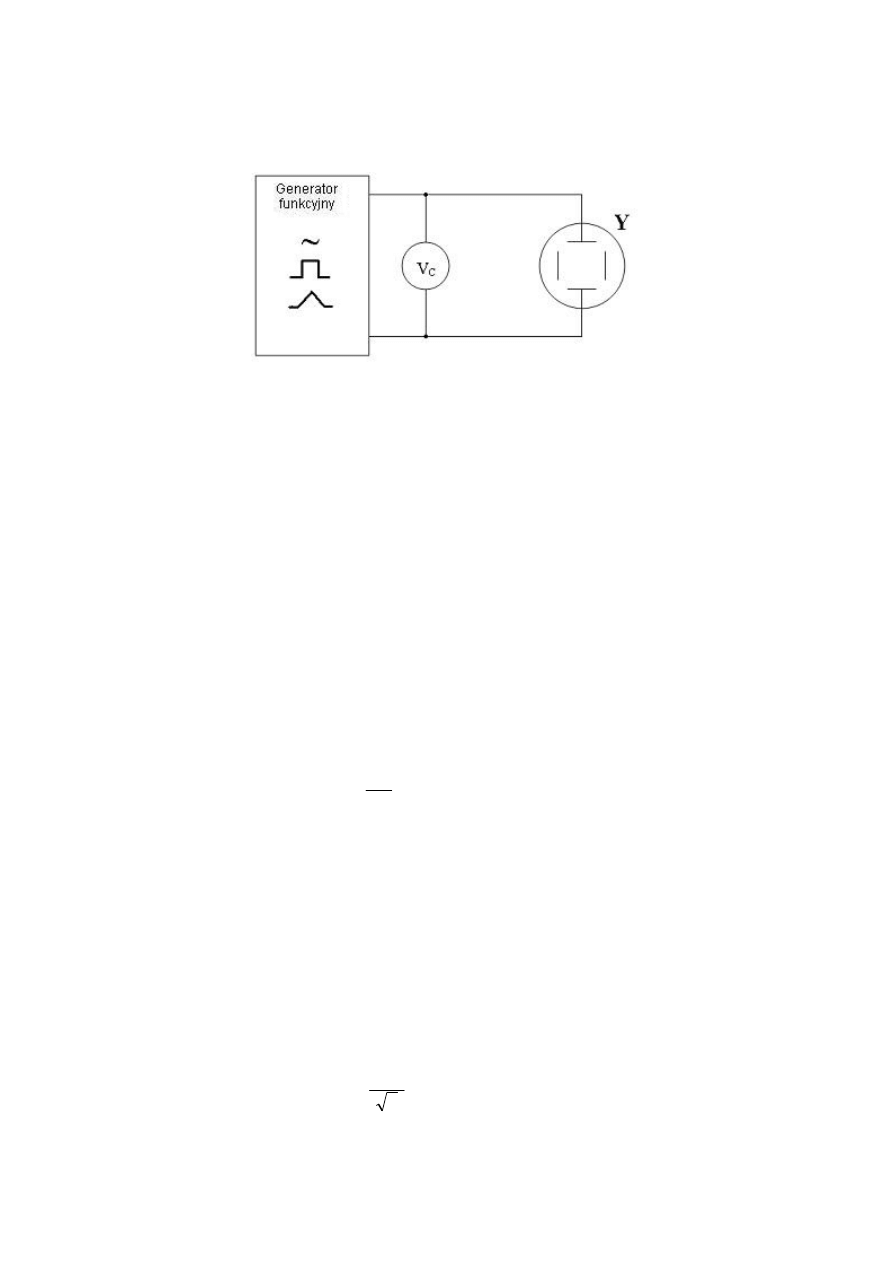
6.3.1. Schemat układu pomiarowego
6.3.2. Oscylogramy i podstawowe parametry przebiegów napięcia
sinusoidalnie zmiennego, prostokątnego oraz trójkątnego.
Dla częstotliwości i napięć podanych przez nauczyciela należy odrysować
z oscyloskopu przebiegi napięcia sinusoidalnie zmiennego, prostokątnego oraz
trójkątnego. W oparciu o oscylogramy wyznaczyć podstawowe parametry przebiegów:
okres, częstotliwość, amplitudę oraz napięcie międzyszczytowe. Zaznaczyć na
oscylogramach następujące wielkości: okres, amplitudę oraz napięcie międzyszczytowe.
Pracować w trybie z włączoną podstawą czasu.
W oparciu o podane wzory należy wykonać obliczenia, a wyniki zanotować obok
oscylogramów.
•
obl
T
– okres obliczony w oparciu o oscylogram
l
P
T
t
obl
⋅
=
– wybrana podstawa czasu
t
P
l
– długość okresu w działkach odczytana z oscylogramu
•
obl
f
– częstotliwość obliczona w oparciu o oscylogram
obl
obl
T
f
1
=
•
gen
f
– częstotliwość przebiegu ustawiona na generatorze
•
obl
m
U
– amplituda przebiegu obliczona w oparciu o oscylogram
l
C
U
y
m
obl
⋅
=
– stała podziałki wejścia Y
y
C
l
– długość amplitudy w działkach odczytana z oscylogramu
•
obl
pp
U
– międzyszczytowa wartość napięcia obliczona w oparciu o oscylogram
obl
obl
m
pp
U
U
⋅
= 2
•
V
U
–skuteczna wartość napięcia wskazywana przez woltomierz
•
obl
U
– obliczona wartość napięcia skutecznego
2
obl
m
obl
U
U
=
2
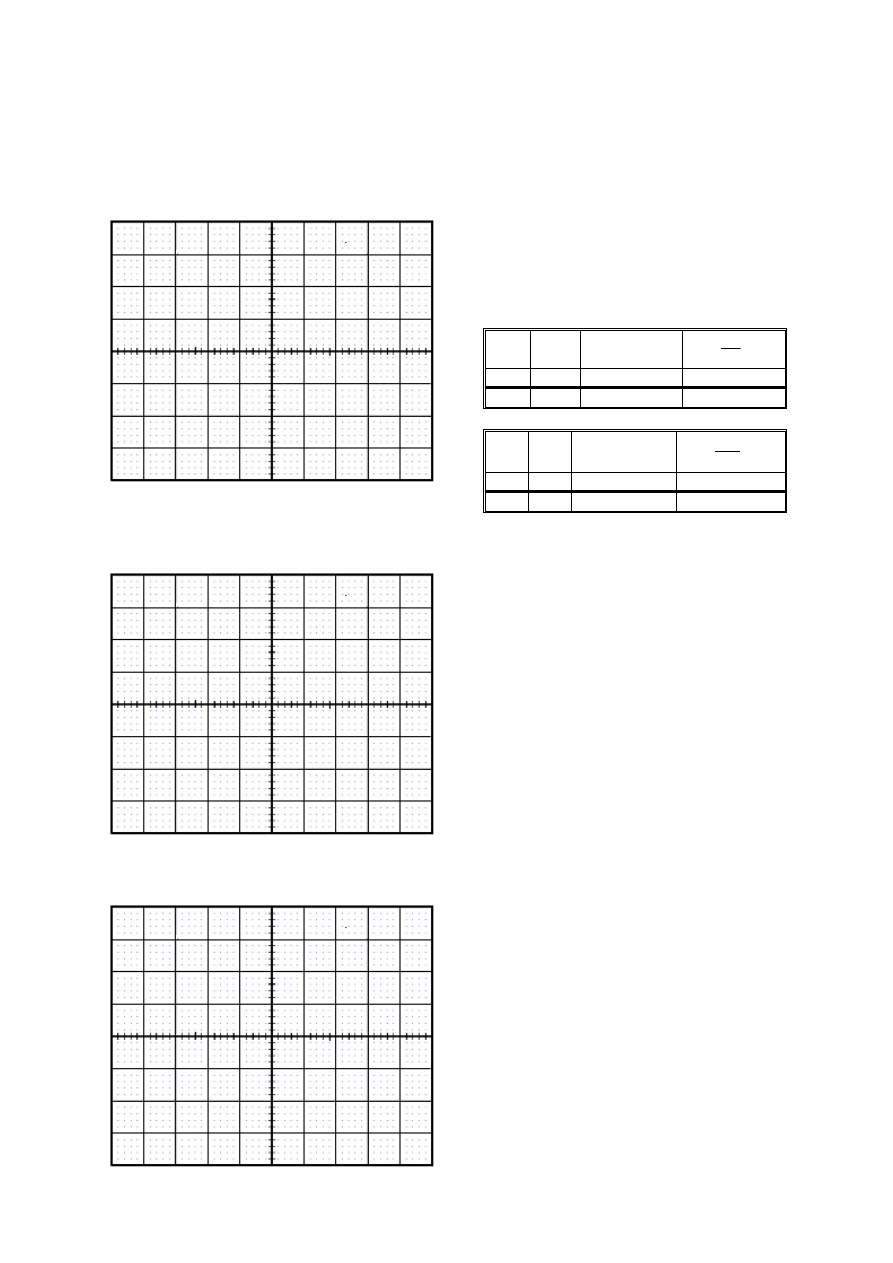
UWAGA:
Na wejście Y oscyloskopu podać sygnał o częstotliwości f = ........... Hz i ustawić
na woltomierzu napięcie U
V
= ........... V (wartości te podaje nauczyciel). Nie zmieniać tych
wartości tylko rodzaj przebiegu (sinusoidalnie zmienny, prostokątny, trójkątny).
t
P
=
......................................
= ......................................
y
C
Przebieg sinusoidalny
obl
T
= ......................................
obl
f
= ......................................
obl
pp
U
= .....................................
U
V
U
obl
V
obl
U
U
U
−
=
Δ
%
100
⋅
Δ
=
V
U
U
U
δ
V V
V
%
f
gen
f
obl
gen
obl
f
f
f
−
=
Δ
%
100
⋅
Δ
=
gen
f
f
f
δ
Hz Hz
Hz
%
Przebieg prostokątny
obl
T
= ......................................
obl
f
= ......................................
obl
pp
U
= .....................................
Przebieg trójkątny
obl
T
= ......................................
obl
f
= ......................................
obl
pp
U
= .....................................
3
6.4. Pomiar nieznanej częstotliwości za pomocą krzywych (figur) Lissajous
Podstawowymi narzędziami do pomiaru częstotliwości przebiegów elektrycznych
są częstościomierze o różnych zasadach działania i budowach. W niektórych badaniach,
szczególnie przy dużych częstotliwościach radiowych stosowana jest metoda zwana
porównawczą, w której wykorzystujemy krzywe Lissajous.
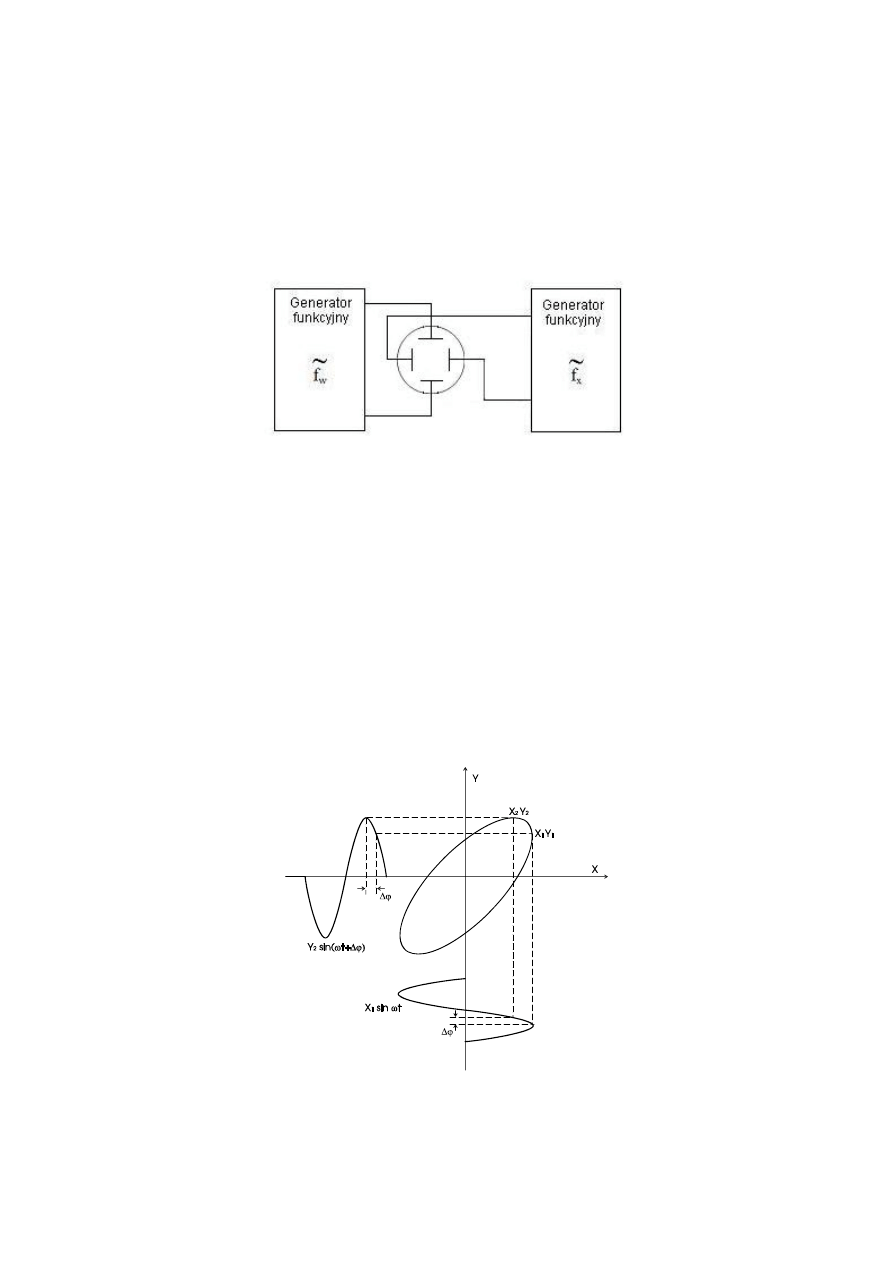
6.4.1. Schemat układu pomiarowego i charakterystyka stosowanej metody
Metoda porównawcza polega na zrównaniu częstotliwości wzorcowej f
w
z częstotliwością mierzoną f
x
. Zgodność częstotliwości można zaobserwować na ekranie
oscyloskopu w postaci krzywych Lissajous. W ten sposób mogą być porównywane tylko
częstotliwości, których stosunek jest liczbą całkowitą. Pomiar metodą porównawczą może
być bardzo dokładny, jeżeli dysponuje się bardzo dokładnym, regulowanym wzorcem
częstotliwości.
Zasadę podłączenia do oscyloskopu napięć o porównywanych częstotliwościach
podaje powyższy rysunek. Dwa napięcia sinusoidalne, doprowadzone do płytek
odchylających X i Y pracującego w trybie dwukanałowym, tworzą na ekranie oscyloskopu
(z wyłączoną podstawą czasu) obrazy, tzw. Krzywe Lissajous, których kształt zależy od
stosunku amplitud, stosunku częstotliwości i przesunięcia fazowego między obydwoma
napięciami. W przypadku, gdy stosunek częstotliwości jest równy stosunkowi liczb
całkowitych, na ekranie oscyloskopu obserwuje się obraz nieruchomy, w innych przypadkach
obraz jest w ciągłym ruchu. Sposób powstawania krzywych Lissajous przedstawia
następujący rysunek:
Wyróżniamy kilka rodzajów krzywych Lissajous, zależy to od stosunku częstotliwości
wzorcowej i częstotliwości mierzonej. Najczęściej mamy do czynienia z krzywymi Lissajous
pierwszego rodzaju (f
w
:f
x
= 1:1). Są niemi elipsa, okrąg i prosta. Czasami możemy mieć
jednak do czynienia z krzywymi Lissajous wyższych rzędów. Przykładowe krzywe Lissajous
wyższych rzędów mają postać:
4
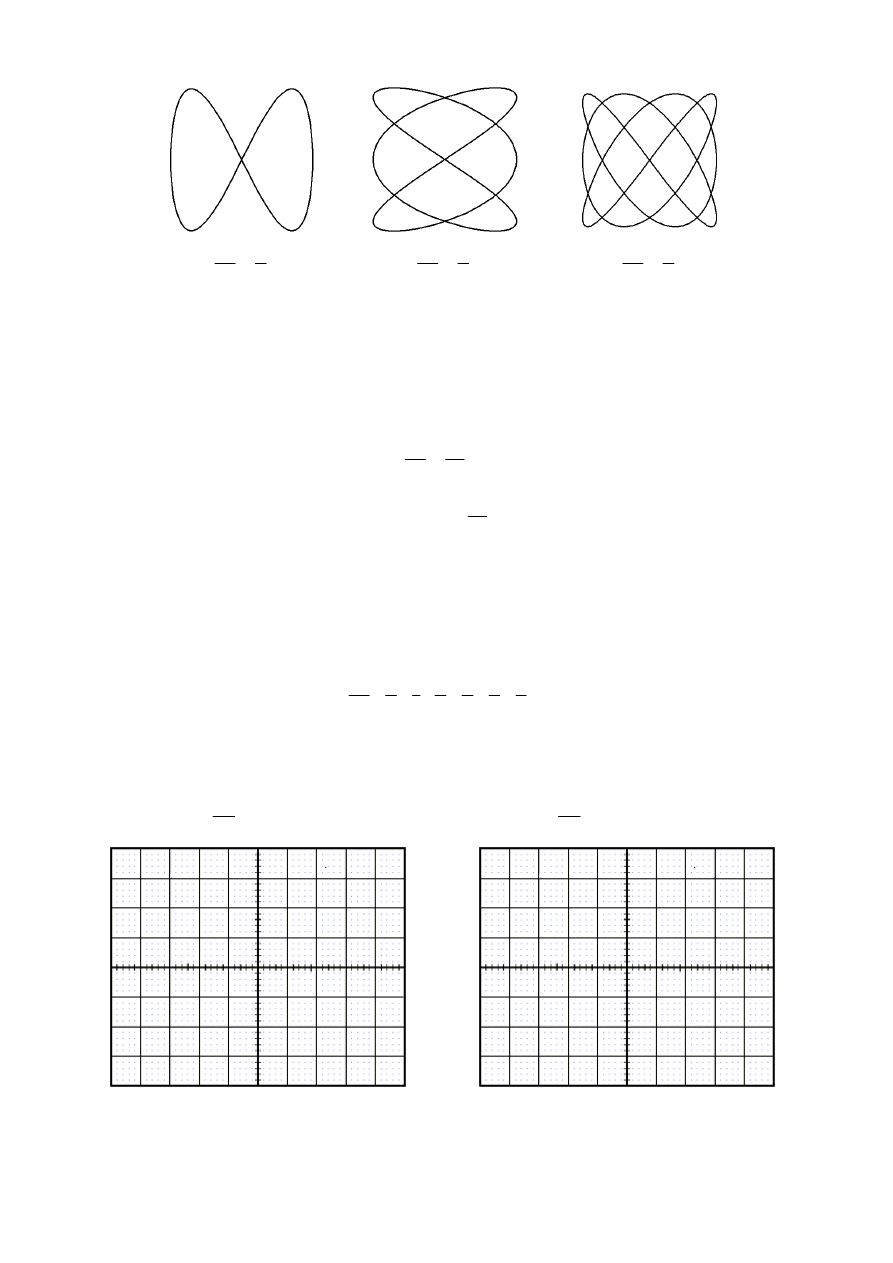
1
2
=
x
w
f
f
3
2
=
x
w
f
f
3
4
=
x
w
f
f
Pomiar
częstotliwości z wykorzystaniem figur Lissajous polega na wyznaczeniu
stosunek częstotliwości wzorcowej i mierzonej. W tym celu oblicza się liczbę punktów
przecięcia krzywej z prosta równoległą do osi poziomej (osi X) oraz liczbę punktów
przecięcia z prostą równoległą do osi pionowej (osi Y). Proste powinny być tak prowadzone,
aby nie przechodziły przez punkty węzłowe krzywych. Następnie obliczenia częstotliwości
nieznanej dokonujemy w oparciu o następujący wzór:
x
y
w
x
y
x
x
w
n
n
f
f
n
n
f
f
⋅
=
=
gdzie: n
x
– liczba punktów przecięcia krzywej z osią poziomą oscyloskopu, n
y
– liczba
punktów przecięcia krzywej z osia pionową, f
w
– częstotliwość podawana z generatora
wzorcowego, f
w
– częstotliwość wzorcowa.
UWAGA:
Odrysować oscylogramy dla dwóch spośród wymienionych stosunków częstotliwości
wskazanych przez prowadzącego
x
w
f
f :
2
1
,
1
1
,
1
2
,
2
3
,
1
6
,
5
3
.
6.4.2. Oscylogramy
..........
..........
..........
=
x
w
f
f
..........
..........
..........
=
x
w
f
f
5
6.5. Pomiar przesunięcia fazowego pomiędzy napięciem i prądem
w obwodzie za pomocą oscyloskopu dwukanałowego
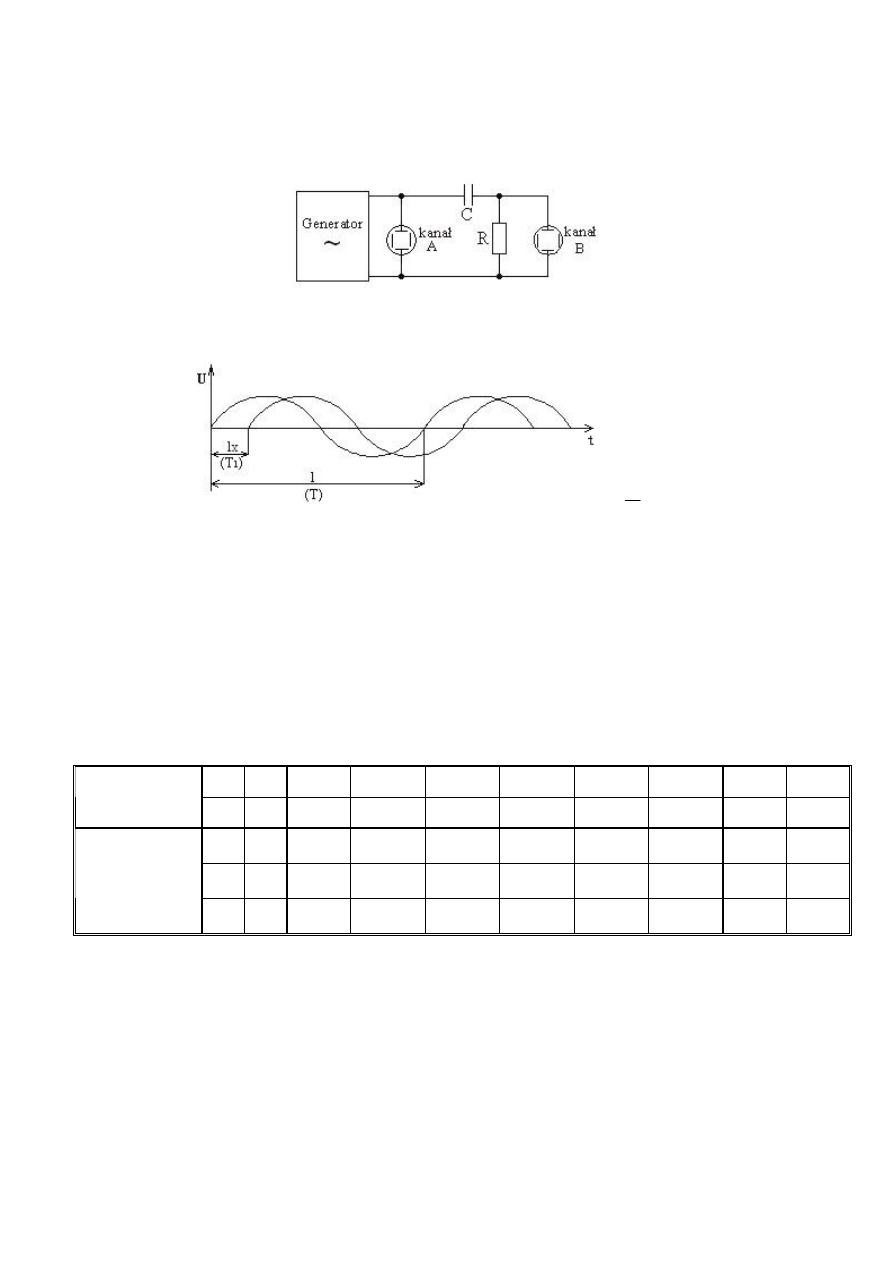
6.5.1. Schemat układu pomiarowego
6.5.2. Rysunek wyjaśniający zasadę pomiaru
ϕ =
0
360
⋅
l
x
l
UWAGA:
Dokonać pomiaru kąta przesunięcia fazowego pomiędzy napięciem sinusoidalnym
podawanym z generatora funkcyjnego i napięciem na rezystorze R. Pracować należy w trybie
z włączoną podstawą czasu oraz w trybie dwukanałowym. Skuteczna wartość napięcia
zmierzona na rezystancji R podzielony prze wartość rezystancji jest równy wartości
skutecznej prądu płynącego w obwodzie.
Wartość rezystancji R oraz pojemności C podaje prowadzący.
6.5.3. Tabela pomiarowa
Lp.
-
1
2
3
4
5
6
7
8
Przesuwnik
fazowy
f
Hz
100
200
300
400
500
600
700
800
l
dz
lx
dz
Przesuwnik 1
C = …….….nF
R = ………..Ω
ϕ
°
6
Document Outline