1
min
620
,
59
05
,
0
25
,
0
log
*
min
027
,
0
303
,
2
log
*
303
,
2
:
/
log
*
303
,
2
*
/*
log
*
303
,
2
log
303
,
2
.......
...
..
1
=
=
−
=
−
=
−
=
−
=
−
M
M
x
a
a
k
t
k
x
a
a
t
k
t
x
a
a
t
k
x
a
a
t
k
reakcji
szybkoć
stala
KINETYKA REAKCJI - zadania dodatkowe
Zadanie 1. Obliczyć czas potrzebny do zmniejszenia stężenia substratu:
a)
z 0,15 M do 0,03 M przy stałej szybkości reakcji k = 0,209 1/min.
b)
z 0,5 M do 0,15 M przy stałej szybkości reakcji k = 0,115 min
-1
.
c)
z 0,1 M do 0,04 M przy stałej szybkości reakcji k = 0,009 s
-1
.
d)
z
0
,
25 M do 0
,
05
M
pr
zy s
t
a
ł
e
j s
zy
bko
ś
ci reakc
j
i k = 0,
027 min
-1
.
t - czas reakcji ?
k = stała szybkość reakcji 0,027 min
-1
a – stężenie początkowe 0,25 M
(a-x) – stężenie końcowe w danym momencie 0,05 M
zamieniamy k na t miejscami
Zadanie 2.
a)
Ile razy wzrosła szybkość pewnej reakcji, jeśli jej temperaturowy współczynnik wynosi γ=5, a
temperatura wzrosła o 8
o
C?
γ
= 5
∆
T = 8
b)
Ile razy wzrosła szybkość pewnej reakcji, jeśli jej temperaturowy współczynnik wynosi γ=6, a
temperatura wzrosła o 5
o
C?
c)
Temperaturowy współczynnik pewnej reakcji wynosi γ=3. O ile stopni należy podnieść temperaturę,
aby szybkość reakcji wzrosła 10 razy?
γ
= 3 Temperaturowy współczynnik pewnej reakcji
∆
T = ? Różnica temperatury
d)
Temperaturowy współczynnik pewnej reakcji wynosi γ=5. O ile stopni należy podnieść temperaturę, aby
szybkość reakcji wzrosła 10 razy?
e)
Temperaturowy współczynnik pewnej reakcji wynosi γ=2. O ile stopni należy podnieść temperaturę, aby
szybkość reakcji wzrosła 3 razy?
f)
Temperaturowy współczynnik pewnej reakcji wynosi γ=4. O ile stopni należy podnieść temperaturę, aby
szybkość reakcji wzrosła 3 razy?
62
,
3
5
10
8
10
1
2
=
=
=
∆Τ
γ
V
V
10
1
2
∆Τ
=
γ
v
v
log
*
10
1
2
∆Τ
=
γ
v
v
10
1
2
log
log
ΛΤ
=
γ
v
v
C
0
83
,
20
83
,
20
48
,
0
:
48
,
0
*
10
10
*
48
,
0
*
10
1
3
log
10
10
log
log
10
10
log
=
∆Τ
∆Τ
=
∆Τ
=
∆Τ
=
∆Τ
=
∆Τ
=
γ

2
Zadanie 3.
Po 5 min
r
eakcji przereagowała połowa substratu o początkowym stężeniu 4 . 10.
5
mol·dm
-3
.
Szybkość maksymalna reakcji wynosiła 2,04 *10
-5
M·min
-1
. Obliczyć K
M
oraz stężenie produktu po
1
0 min.
1.
t = 5 min / połowa substratu / po 10 min
2.
[S] = 4* 10
-5
mol * dm
-3
.
3.
V max = 2,04 *10
-5
M·min
-1
4.
k = ? Stała szybkości reakcji
5.
v = ?
Szybkość początkowa reakcji
6.
K
M
= ? Stała Michaelisa.
[S]
5
= a-x = 50% [S] = 0,5 * 4* 10
-5
mol * dm
-3
= 2* 10
-5
mol * dm
-3
Stężenie produktu po 10 min?
1.
t = 10 min
2.
[S] = stężenie substratu 4* 10
-5
mol * dm
-3
.
3.
k =
stała szybkość reakcji
0, 139 min-
1
4.
( a - x) stężenie substratu po 10 min
5.
x = ? Stężenie produktu po 10 min
zamiana miejscami
1
3
5
3
5
min
139
,
0
*
10
*
2
*
10
*
4
log
min
5
303
,
2
)
(
log
1
−
−
−
−
−
=
=
−
=
dm
mol
dm
mol
x
a
a
t
k
1
6
5
1
min
*
10
*
78
,
2
10
*
2
*
min
139
,
0
)
(
*
−
−
−
−
=
=
−
=
M
x
a
k
v
(
)
t
x
a
a
t
k
*
log
303
,
2
−
=
(
)
303
,
2
:
log
303
,
2
x
a
a
kt
−
=
(
)
x
a
a
kt
−
=
log
303
,
2
(
)
303
,
2
log
kt
x
a
a
=
−
(
)
303
,
2
10
kt
x
a
a
=
−
(
)
303
,
2
10
*
139
,
0
10
=
−
x
a
a
(
)
603
,
0
10
=
−
x
a
a
(
)
(
)
x
a
x
a
a
−
=
−
603
,
0
10
(
)
603
,
0
10
*
x
a
a
−
=

3
Odp. Stężenie substratu po 10 min wynosi 1*10
-5
mol/dm
-3
.
Odp. Po 10 min powstało 3*10
-5
mol.*dm
-3
produktu.
a) Po 5 min reakcji przereagowała połowa substratu o początkowym stężeniu 3
⋅
10
-5
mol
⋅
dm
-3
. Szybkość
maksymalna reakcji wynosiła 4,02
⋅
10
-5
M
⋅
min
-1
. Obliczyć K
M
oraz stężenie produktu po 10 min.
b) Po 3 min reakcji przereagowała połowa substratu o początkowym stężeniu 4
⋅
10
-3
mol
⋅
dm
-3
. Szybkość
maksymalna reakcji wynosiła 12
⋅
10
-3
M
⋅
min
-1
. Obliczyć K
M
oraz stężenie produktu po 9 min.
Zadanie 4.
Stała Mi
c
haelisa w reakcji hydrolizy peptydu wynosi 4 . 10
-3
M. Przy stężeniu początkowym
substratu 8 . 10
-5
M, po 2 minutach zhydrolizowało 10% peptydu. Obliczyć stałą szybkości reakc
ji
oraz
szybkość maksymalną V
max
K
M
= 4*10
-3
M
[S
0
] = 8*10
-5
[S
1
] = (a-x) zhydrolizowało 10% peptydu to pozostało 90%. 90% z 8 = 0,9 * 8 * 10
-5
= 7,02 * 10
-5
V max = ?
k = ?
v = ?
a)
Stała Michaelisa w reakcji hydrolizy peptydu wynosi 2
⋅
10
-3
M. Przy stężeniu początkowym substratu 4
⋅
10
-5
M, po 2 minutach zhydrolizowało 20% peptydu. Obliczyć stałą szybkości reakcji oraz szybkość
maksymalną V
max
.
b)
Stała Michaelisa w reakcji hydrolizy peptydu wynosi 12
⋅
10
-5
M. Przy stężeniu początkowym substratu
3
⋅
10
-5
M, po 2 minutach zhydrolizowało 15% peptydu. Obliczyć stałą szybkości reakcji oraz szybkość
maksymalną V
max
.
(
)
1
5
5
min
065
,
0
10
*
02
,
7
10
*
8
log
min
2
303
,
2
log
303
,
2
−
−
−
=
=
−
=
M
M
x
a
a
t
k
(
)
6
5
10
*
56
,
4
10
*
02
,
7
*
065
,
0
−
−
=
=
−
=
x
a
k
v
[ ]
[ ]
[ ]
max
1
*
1
*
1
max
V
S
K
v
S
K
S
K
V
v
M
M
M
=
+
+
+
=
[ ]
3
6
5
3
max
max
10
*
28
,
2
10
*
56
,
4
*
1
10
*
8
10
*
4
*
1
−
−
−
−
=
+
=
+
=
V
v
S
K
V
M
(
)
603
,
0
603
,
0
10
:
10
*
x
a
a
−
=
x
a
a
−
=
603
,
0
10
4
10
*
4
-5
=
−
x
a
3
5
5
*
10
*
1
4
10
*
4
−
−
−
=
=
−
dm
mol
x
a
5
10
*
1
−
−
=
x
a
3
5
5
5
/
10
*
3
10
*
1
10
*
4
−
−
−
−
=
−
=
dm
mol
a
4
10
*
4
)
(
5
−
=
−
x
a

4
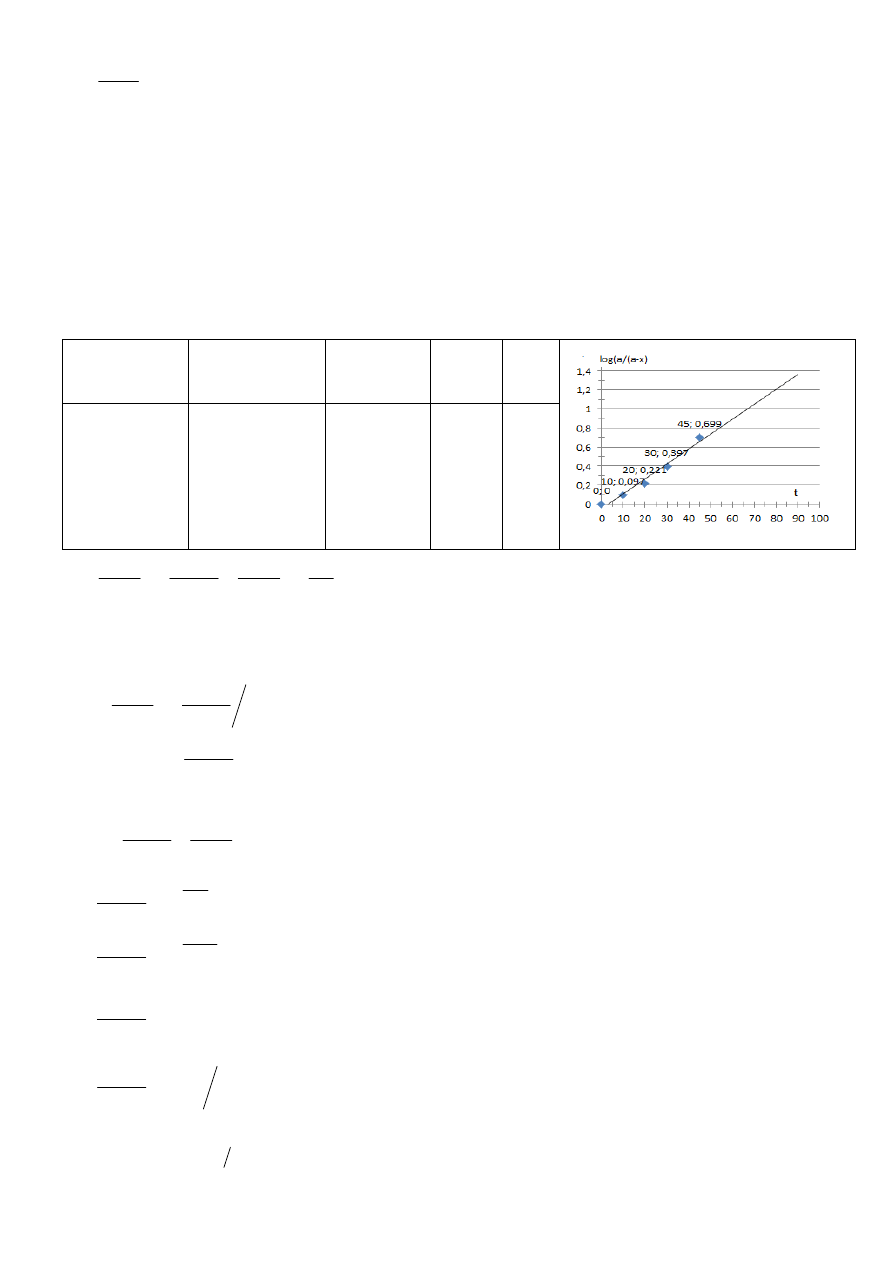
Zadanie 5. Określić rząd reakcji oraz obliczyć stałą szybkości reakcji denaturacji białka o stężeniu
15
mg/cm
3
,
jeśli uzyskano następujące wyniki:
Ile białka natywnego pozostanie w roztworze po 15 min ogrzewania?
zamiana miejscami
Czas
ogrzewania
[min]
Stężenie białka
natywnego
[mg/cm
3
]
(a
-
x)
Stężenie białka
zdenaturowanego
[x]
log(a/(a-
x)) i
1/(a-x)
0
2
4
6
8
10
15,0
14,0
13,0
12,0
11,0
10,0
0
15-
14
=1
2
3
4
5
0
0,03
0,06
0,09
0,13
0,17
0,067
0,071
0,076
0,083
0,091
0,1
(
)
1
min
35
,
1
1
15
log
2
303
,
2
log
303
,
2
−
=
=
−
=
x
a
a
t
k
(
)
t
x
a
a
t
k
*
log
303
,
2
−
=
(
)
303
,
2
:
log
303
,
2
x
a
a
kt
−
=
(
)
x
a
a
kt
−
=
log
303
,
2
(
)
303
,
2
log
kt
x
a
a
=
−
(
)
303
,
2
10
kt
x
a
a
=
−
(
)
303
,
2
15
*
35
,
1
10
=
−
x
a
a
(
)
79
,
8
10
=
−
x
a
a
(
)
(
)
x
a
x
a
a
−
=
−
79
,
8
10
(
)
79
,
8
10
*
x
a
a
−
=
(
)
79
,
8
79
,
8
10
:
10
*
x
a
a
−
=
x
a
a
−
=
79
,
8
10
79
,
8
10
a
x
a
=
−
5
Odp. po 15 min zostało 2,43*10
-8
białka natywnego.
Odp. po 15 minutach białka denaturowanego powstanie 14,99 mg/cm
3
Zadanie 6.
Określić rząd reakcji oraz obliczyć stałą szybkości reakcji hydrolizy skrobi, jeśli uzyskano następujące
stężenie produktu:
Czas
ogrzewania
[min]
Stężenie
produktu
[mg/cm
3
]
(a-x)
3
log(a/(a-
x)) i
1/(a-
x)
0
10
20
30
45
60
90
0
0,6
1,2
1,8
2,4
3,0
3,0
3
3-0,6=2,4
1,8
1,2
0,6
0
0
0
0,097
0,221
0,397
0,699
0,33
0,42
0,56
0,83
0,42
Ile skrobi pozostanie w roztworze po 120 min ogrzewania?
Zamiana miejscami
(
)
1
min
02
,
0
4
,
2
3
log
10
303
,
2
log
303
,
2
−
=
=
−
=
x
a
a
t
k
(
)
t
x
a
a
t
k
*
log
303
,
2
−
=
(
)
x
a
a
kt
−
=
log
303
,
2
(
)
303
,
2
log
kt
x
a
a
=
−
(
)
303
,
2
10
kt
x
a
a
=
−
(
)
04
,
1
10
=
−
x
a
a
(
)
303
,
2
10
*
02
,
0
10
=
−
x
a
a
(
)
(
)
x
a
x
a
a
−
=
−
*
10
04
,
1
(
)
04
,
1
04
,
1
10
10
*
x
a
a
−
=
8
79
,
8
10
*
43
,
2
10
15
−
=
=
−
x
a
8
10
*
43
,
2
−
−
=
x
a
3
8
/
99
,
14
10
*
43
,
2
15
cm
mg
a
=
−
=
−
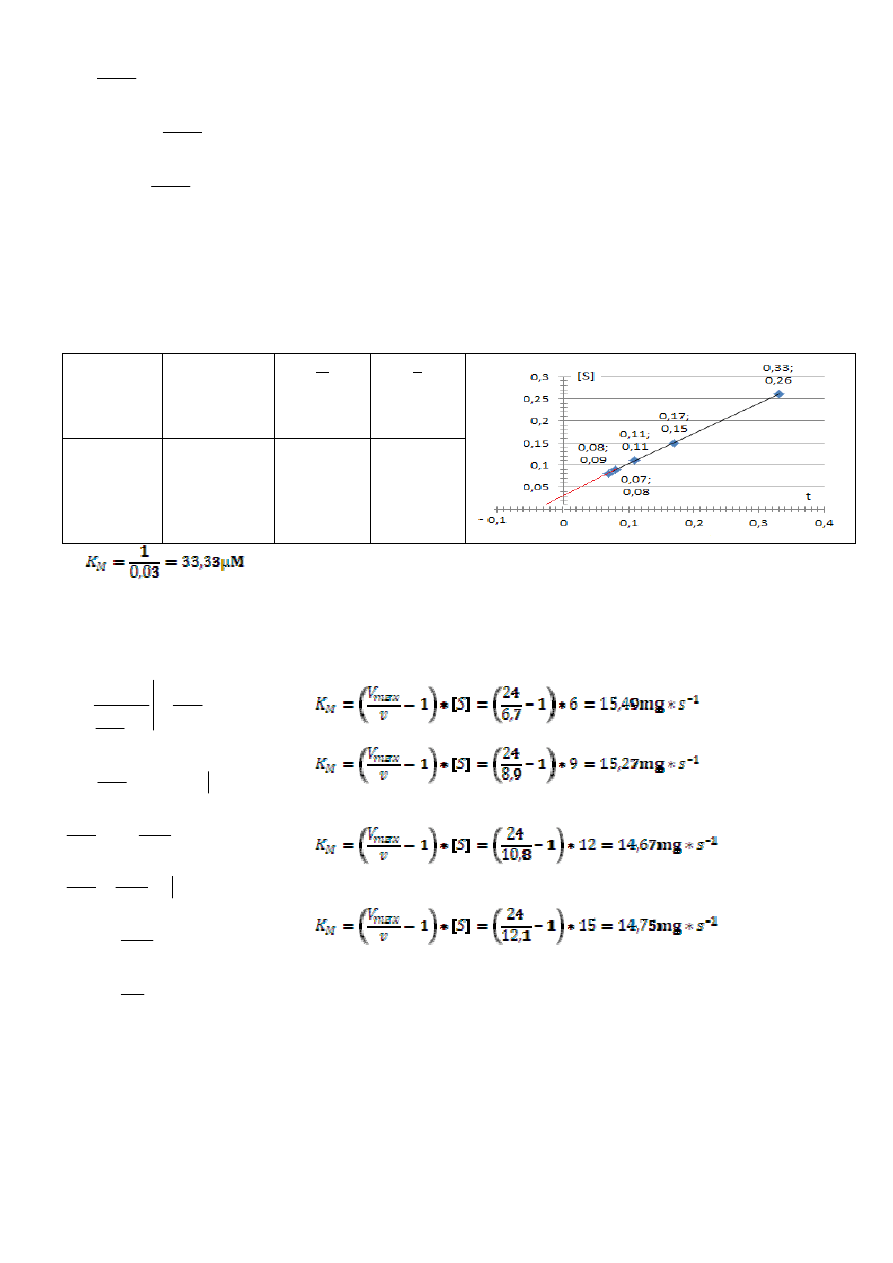
6
Po 120 min zostanie 0,27 mg/cm
3
skrobi.
Zadanie 7.
Oznaczono szybkości początkowe v
0
dla reakcji enzymatycznej przy różnych stężeniach substratu:
Początkowe
stężenie
substratu
[µM]
Szybkość
początkowa
v
0
[mg
⋅
s
-1
]
1
[S]
1
[V
0
]
3
6
9
12
15
3,9
6,7
8,9
10,8
12,1
0,33
0,17
0,11
0,08
0,07
0,26
0,15
0,11
0,09
0,08
Wartość szybkości maksymalnej V
max
= 24,0 mg
⋅
s
-1
. Obliczyć K
M
oraz podać dla jakiego stężenia substratu
szybkość reakcji osiągnie wartość maksymalną.
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
1
-
max
max
max
max
max
s
mg
46
,
15
3
*
1
9
,
3
24
*
1
*
1
1
:
1
*
1
*
1
=
−
=
−
=
−
=
=
+
=
+
+
+
=
M
M
M
M
M
M
M
K
S
v
V
K
S
v
V
S
K
v
V
S
K
v
V
S
K
v
S
K
S
K
V
v
(
)
x
a
a
−
=
04
,
1
10
(
)
04
,
1
10
a
x
a
=
−
3
04
,
1
/
27
,
0
10
3
)
(
cm
mg
x
a
=
=
−
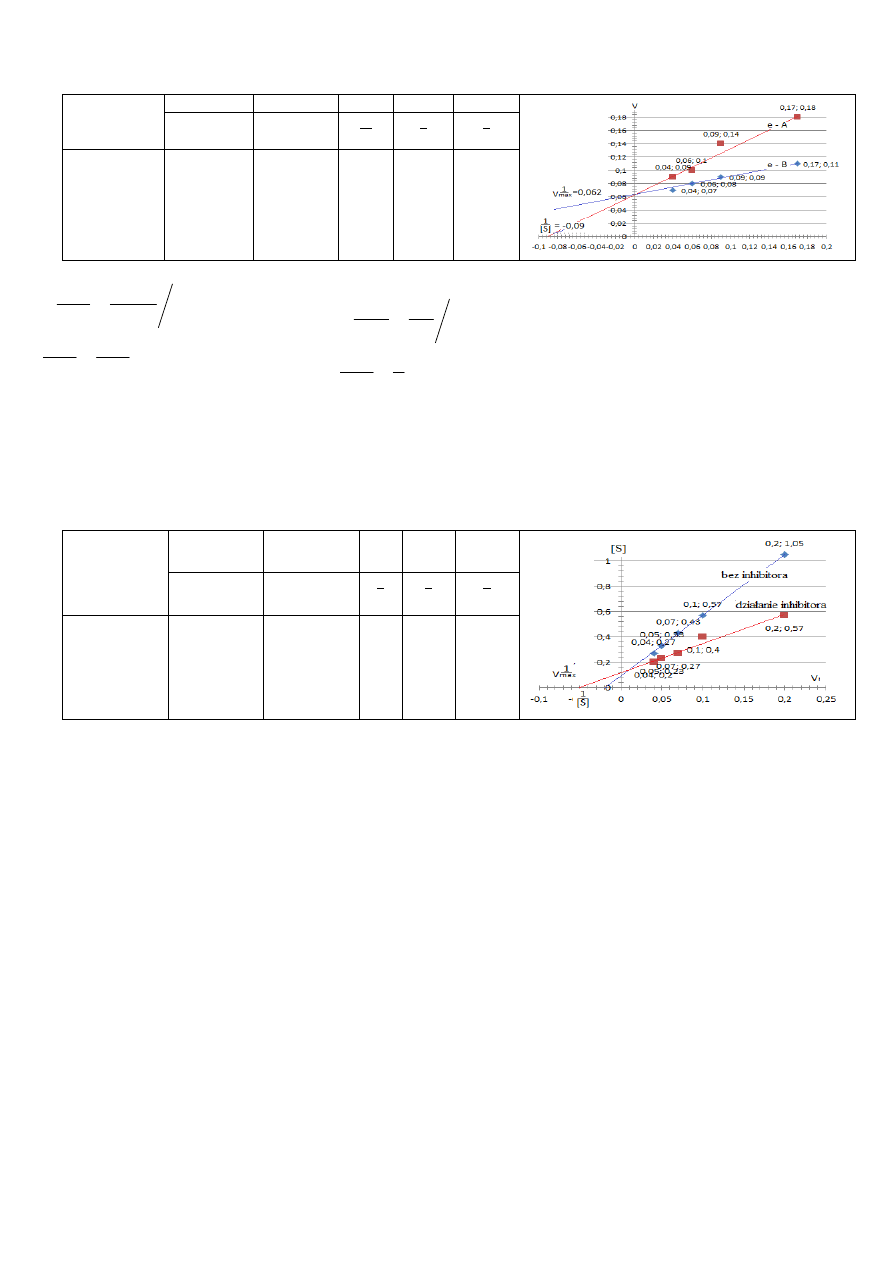
7
Zadanie 8. W wyniku działania dwóch różnych enzymów na substrat o zmiennym stężeniu określono
szybkości początkowe:
enzym A
enzym B
e - A
e - B
Początkowe
stężenie
substratu [µM]
v
0
[µ M
⋅
min
-1
]
v
0
[µ M
⋅
min
-1
]
1
[S]
1
[V
0
]
1
[V
0
]
5,8
10,2
15,6
25,0
8,7
11,1
12,5
13,7
5,3
7,4
9,3
11,1
0,17
0,09
0,06
0,04
0,11
0,09
0,08
0,07
0,18
0,14
0,10
0,09
a)
Określić stałe kinetyczne K
M
i V
max
metodą podwójnych odwrotności.
b)
Który z enzymów wykazuje większe powinowactwo do substratu? –
eB
c)
Określić rodzaj inhibicji – kompetencyjna.
d)
Podać w jaki sposób można cofnąć działanie inhibitora – dodając substratu.
Zadanie 9.
Oznaczono szybkości początkowe reakcji bez i z dodatkiem inhibitora. Otrzymano:
bez
inhibitora
działanie
inhibitora
bez /
inh.
dz /
inh.
Początkowe
stężenie
substratu
[µM]
v
0
[µM
⋅
min
-1
]
v
0
[µM
⋅
min
-1
]
1
[S]
1
[V
0
]
1
[V
0
]
5
10
15
20
25
0,95
1,74
2,35
3,03
3,64
1,74
2,50
3,64
4,44
5,00
0,2
0,1
0,07
0,05
0,04
1,05
0,57
0,43
0,33
0,27
0,57
0,4
0,27
0,23
0,2
a)
Wyznaczyć stałe kinetyczne
b)
Określić rodzaj inhibicji - kompetencyjna.
c)
Podać w jaki sposób można cofnąć działanie inhibitora – związki wiążące inhibitor…
Zadanie 10.
a)
Stała Michaelisa w reakcji hydrolizy peptydu wynosi 3
⋅
10
-3
M. Przy stężeniu początkowym substratu 6
⋅
10
-5
M, po 5 minutach zhydrolizowało 30% peptydu. Obliczyć stałą szybkości reakcji oraz szybkość
maksymalną V
max
oraz stężenie produktu po 10 min.
b)
Po 5 min reakcji przereagowała połowa substratu o początkowym stężeniu 3
⋅
10
-5
mol
⋅
dm
-3
. Szybkość
maksymalna reakcji wynosiła 2,02
⋅
10
-5
M
⋅
min
-1
. Obliczyć K
M
oraz stężenie produktu po 10 min.
c)
Po 3 min reakcji przereagowało 15% substratu o początkowym stężeniu 4
⋅
10
-3
mol
⋅
dm
-3
. Szybkość
maksymalna reakcji wynosiła 8
⋅
10
-3
M
⋅
min
-1
. Obliczyć K
M
oraz stężenie produktu po 8 min.
1
1
1
min
*
1
,
11
09
,
0
1
1
)
1
(
*
09
,
0
1
1
−
=
=
−
−
=
−
M
K
K
M
M
µ
1
1
2
min
*
5
,
0
2
1
1
)
1
(
*
2
1
1
−
=
=
−
−
=
−
M
K
K
M
M
µ
Wyszukiwarka
Podobne podstrony:
A cw 2 koło 1 kinetyka reakcji zadania dodatkowe 2
KINETYKA REAKCJI, Matury i zadania maturalne z chemii
06 Kinetyka reakcji enzymatycznych
4 Badanie kinetyki reakcji zmy Nieznany (2)
w 1 - wartość pieniądza w czasie - zadania dodatkowe, wszop ZZIP, II semestr, finanse i rachunkowość
04 Kinetyka reakcji chemicznych i kataliza
kinetyka reakcji enzymatycznych I
Noworyta, inżynieria bioreaktorów, równania kinetyczne reakcji
Cwiczenia nr 4 zadanie dodatkowe 4
zadania dodatkowe, Ekonomia- studia, Finanse publiczne i rynki finansowe
Zadania dodatkowe, FINANSE PRZEDSIĘBIORSTW JAWORSKI, finanse przedsiębiorstw
Zadanie dodatkowe nr 1
Zadanie dodatkowe dla chętnych
kinetyka reakcji
15 Kinetyka reakcji 1 rzedu
Kinetyka reakcji inwersji sacharozy
m2 dynamika koła zadanie dodatkowe
więcej podobnych podstron