Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
1
CZĘŚĆ 1
UWAGI WSTĘPNE
Przemianą gazu zawartego w układzie nazywa się ciągłą zmianę jego stanu
termodynamicznego
(określanego przez parametry stanu gazu, którymi są: ciśnienie,
temperatura, objętość właściwa). Do bliższego określenia przemiany nie wystarczy znajomość
stanu początkowego i końcowego. Należy również podać, w jaki sposób ta przemiana dokonuje
się. Sposób zmiany stanu termodynamicznego odwzorowany w odpowiednim układzie
parametrów stanu wyznacza krzywą, którą nazywa się drogą przemiany.
Przemia
ny mogą odbywać się w układach zamkniętych i w układach otwartych. Za
układ zamknięty uznaje się układ o stałej ilości substancji (czynnika termodynamicznego) w nim
zawartej, przy czym substancja do niego nie dopływa ani z niego nie odpływa. Układ, przez
k
tóry przepływa substancja jest otwarty. Przykładem przemiany w układzie zamkniętym może
być ogrzewanie gazu w zamkniętym zbiorniku lub rozprężanie gazu w cylindrze maszyny
tłokowej z zamkniętymi zaworami. Przemianę w układzie otwartym stanowi przepływ gazu
w
rurociągu.
Przemiany mogą być odwracalne i nieodwracalne. W przemianie odwracalnej po
dokonaniu przemiany jest możliwy powrót do stanu wyjściowego układu i otoczenia. Jeśli
powrót układu do stanu wyjściowego jest związany ze skończonymi zmianami w stanie
otoczenia to układ podlega przemianie nieodwracalnej.
Rozważane będą przemiany gazów doskonałych odbywające się w układach
zamkniętych, odwracalne, charakteryzujące się stałym ciepłem właściwym (przemiany
politropowe).
Zgodnie z pierwszą zasadą termodynamiki stan termodynamiczny czynnika w układzie
zamkniętym można zmienić przez wymianę z otoczeniem energii w postaci pracy lub ciepła.
Pomiędzy dwoma stanami czynnika termodynamicznego można zrealizować
nieskończenie wiele przemian termodynamicznych. Zmiana sposobu przejścia pomiędzy
obydwoma stanami powoduje zmianę ilości wykonanej pracy oraz zmianę ilości pochłoniętego
ciepła. Jeżeli rozpatrywana przemiana przebiega w układzie zamkniętym, to różnica wykonanej
pracy i ciepła pochłoniętego przez czynnik jest niezależna od drogi przemiany, gdyż zgodnie
z
równaniem pierwszej zasady termodynamiki, wyraża ona spadek energii wewnętrznej.
Praca wymieniana z otoczeniem jest przedstawiana w układzie współrzędnych p – v
zwanym wykresem pracy
a ciepło wymieniane z otoczeniem jest przedstawiane w układzie
współrzędnych T – s zwanym wykresem ciepła (gdzie s jest oznaczeniem entropii).
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
2
ENTROPIA
Entropia jest kolejną, oprócz energii wewnętrznej i entalpii, funkcją stanu
termodynamicznego. Będzie wykorzystana do wprowadzenia wykresu przemiany w układzie
współrzędnych temperatura bezwzględna – entropia, zwanego wykresem ciepła. Entropia jest
określana zależnością:
T
dQ
dS
i ma wymiar [J/K].
W odniesieniu do 1 kg czynnika jest zapisywana następująco:
T
dq
ds
i ma wymiar [J/(kg∙K)].
W powyższym wyrażeniu dq przedstawia pewną skończoną porcję ciepła, a T średnią
temperaturą tego ciepła.
W obliczeniach przyjmuje się zwykle, że entropia ciała jest równa zeru wtedy, gdy ciało
ma temperaturę 273 K i znajduje się pod ciśnieniem 101325 Pa.
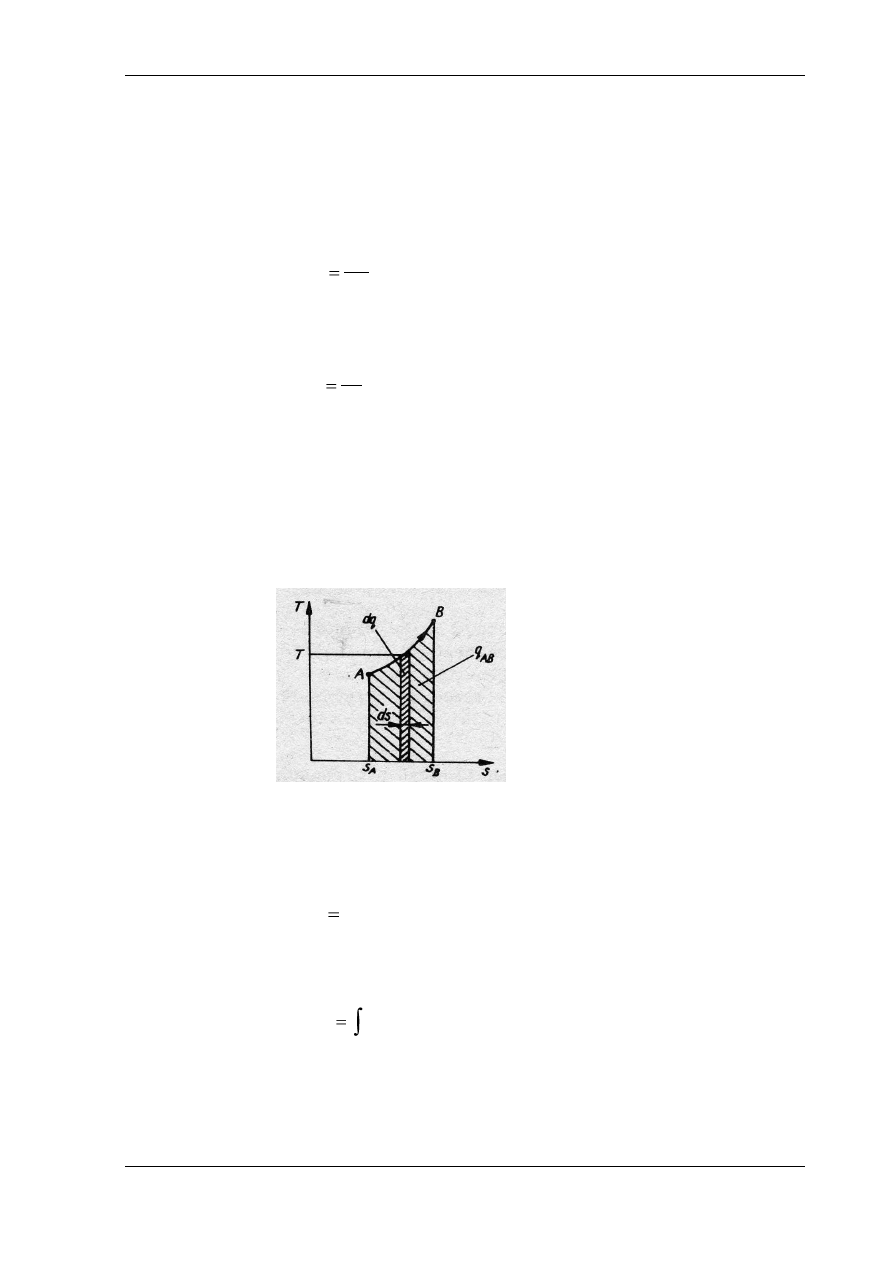
Wykres ciepła – układ współrzędnych T-s
Krzywa A -
B przedstawia dowolną zmianę stanu układu w układzie współrzędnych T – s.
Jeśli wyodrębnić elementarne pole o podstawie ds i średniej rzędnej T, to elementarny przyrost
ciepła dq będzie reprezentować pole stanowiące iloczyn T∙ds:
ds
T
dq
Wtedy
przyrost energii układu dostarczonej za pośrednictwem ciepła z otoczenia po drodze A-B
będzie równy:
B
A
AB
ds
T
q
Ten przyrost energii przedstawi
a pole zakreskowane pod krzywą A-B. W przypadku
dodatniego przyrostu entropii pole pod krzywą przedstawia ciepło dostarczone do
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
3
układu, a w przypadku ujemnego przyrostu entropii pole pod krzywą A-B przedstawia
ciepło oddane przez układ do jego otoczenia.
Pojęcie entropii jest trudne do prostego zdefiniowania. Względnie łatwo jest obliczyć jej
zmiany. Treść fizyczna entropii w termodynamice fenomenologicznej
1
(tutaj rozpatrywanej)
sprowadza się do takiej funkcji stanu, która w procesie termodynamicznym (quasistatycznym)
równa się stosunkowi ciepła pobranego przez układ w temperaturze bezwzględnej, do tej
temperatury, czyli:
T
dq
ds
Zakładając, że dq przedstawia skończoną porcję ciepła otrzymuje się:
T
q
s
Jeśli Δq będzie dzielić się przez niewielką liczbę stopni temperatury T, to przyrost Δs będzie
duży; natomiast gdy liczba stopni jest duża, to przyrost Δs jest mały. A zatem, przyrost entropii
Δs jest miarą jakości wkładu ciepła:
Δs duże – zła lokata ciepła, marnowanie jakości energii cieplnej,
Δs małe – ciepło ulokowane korzystnie.
A zatem, ciepło należy doprowadzać przy jak najwyższej temperaturze.
PRZEMIANA POLITROPOWA
WYPROWADZE
NIE RÓWNANIA PRZEMIANY POLITROPOWEJ
Przemiana politropowa charaktery
zuje się tym, że ciepło właściwe podczas przemiany jest
stałe:
.
const
dT
dq
c
Równanie przemiany politropowej we współrzędnych p-v można wyprowadzić
z I zasady termodynamiki:
dv
p
dT
c
dq
v
Ponieważ dla politropy:
dT
c
dq
,
więc:
0
dv
p
dT
c
dT
c
v
1
Termodynamika fenomenologiczna
– metoda badań zjawisk termodynamicznych polegająca na badaniu związków
między wielkościami makroskopowymi badanego układu termodynamicznego: temperaturą, ciśnieniem, energią, nie
wnikając w mikrostrukturę czynnika.
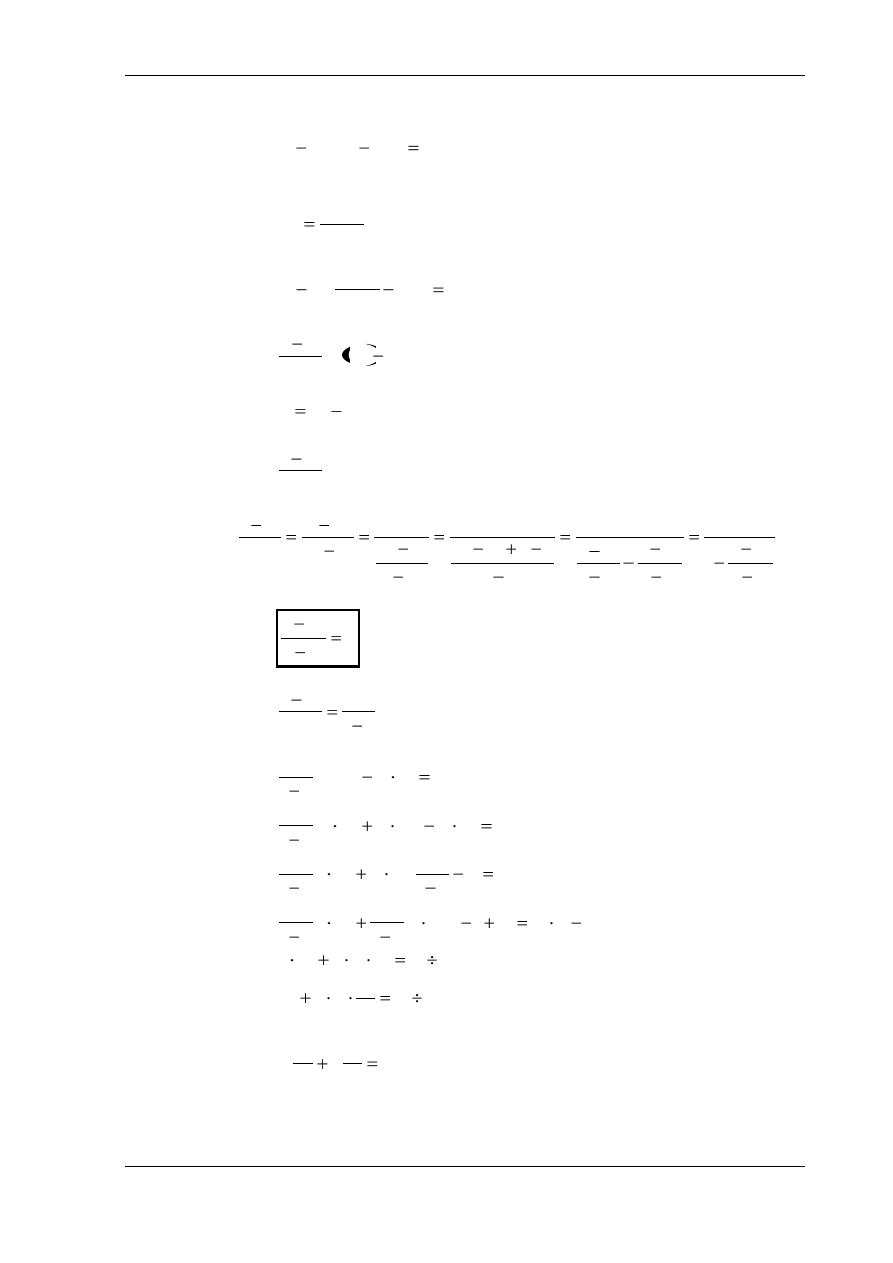
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
4
lub:
0
)
(
dv
p
dT
c
c
v
(1)
Z równania stanu:
R
pv
d
dT
)
(
Po podstawieniu do (1) otrzymuje się:
0
)
(
)
(
dv
p
R
pv
d
c
c
v
lub:
dv
p
pv
d
R
c
c
v
(2)
Ponieważ:
v
p
c
c
R
to wyrażenie :
R
c
c
v
można przekształcić do postaci
v
p
v
p
c
v
v
v
p
v
v
p
v
p
v
v
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
R
c
c
1
1
1
1
1
Oznaczając:
n
c
c
c
c
v
p
(3)
gdyż jest to wielkość stała dla danej przemiany, otrzymuje się:
n
R
c
c
v
1
1
Stąd po podstawieniu do (2) i dokonaniu przekształceń:
p
v
dv
p
n
dp
v
dv
p
n
dp
v
n
n
dv
p
n
dp
v
n
n
dv
p
dp
v
n
dv
p
dv
p
dp
v
n
dv
p
pv
d
n
/
0
/
0
)
1
(
/
0
)
1
1
(
1
1
1
1
0
)
1
1
1
(
1
1
0
)
(
1
1
0
)
(
1
1
otrzymuje się równanie różniczkowe politropy:
0
v
dv
n
p
dp
(4)
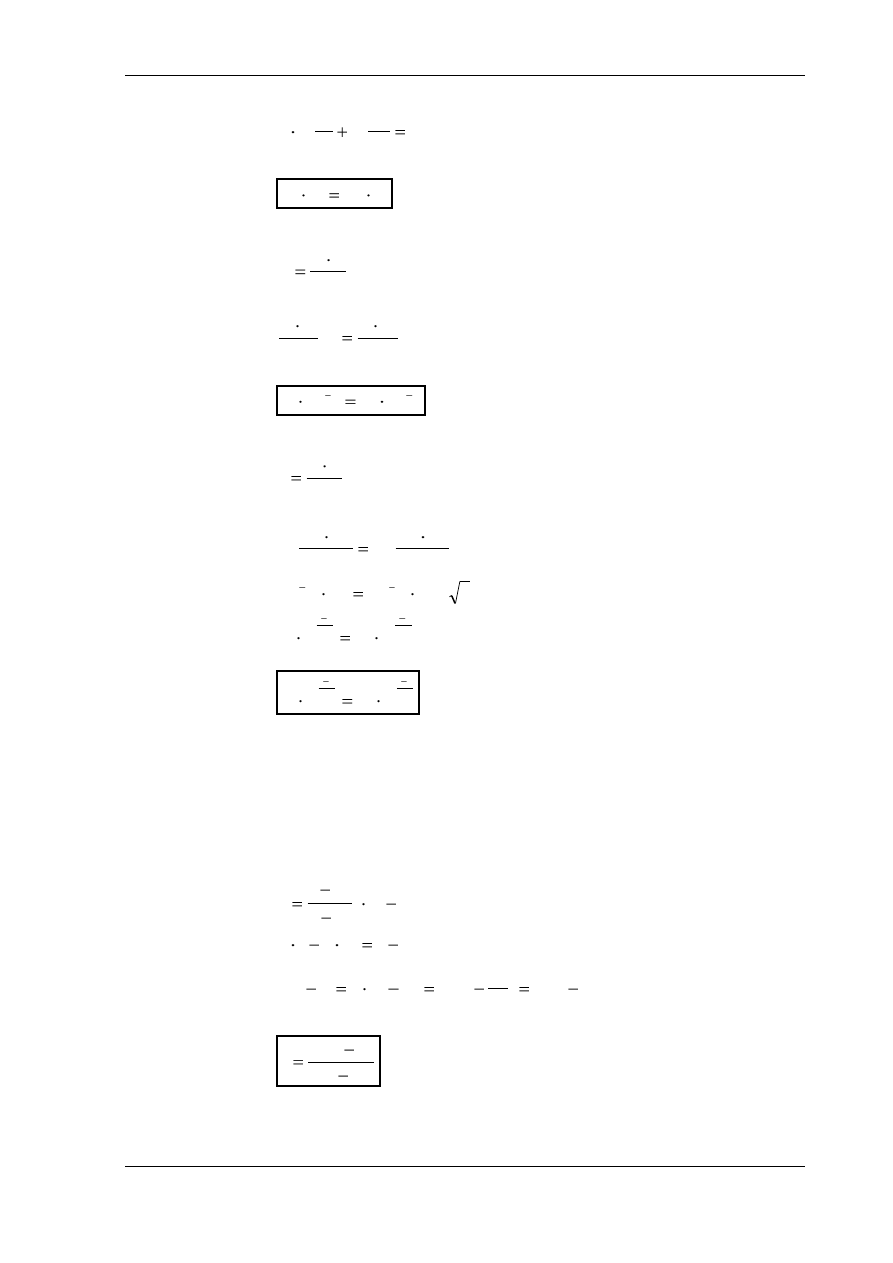
Po scałkowaniu równania (4) otrzymuje się:
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
5
0
ln
ln
1
2
1
2
p
p
v
v
n
lub:
n
n
v
p
v
p
2
2
1
1
(5)
Wykorzystując równanie stanu gazu można otrzymać inną postać tego równania. Podstawiając
do równania (5):
v
T
R
p
i dokonując przekształceń:
n
n
v
v
T
R
v
v
T
R
2
2
2
1
1
1
otrzymuje się:
)
1
(
2
2
)
1
(
1
1
n
n
v
T
v
T
(6)
Podstawiając do równania (5):
p
T
R
v
i dokonując przekształceń:
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
p
T
p
T
T
p
T
p
p
T
R
p
p
T
R
p
1
2
2
1
1
1
2
)
1
(
2
1
)
1
(
1
2
2
2
1
1
1
/
otrzymuje się
n
n
n
n
p
T
p
T
1
2
2
1
1
1
(7)
CIEPŁO WŁAŚCIWE PRZEMIANY POLITROPOWEJ
Wykorzystując definicję wykładnika politropy (3) można otrzymać zależność pozwalającą
obliczyć wartość ciepła właściwego przemiany, jeśli jest znany wykładnik politropy n:
)
(
)
(
)
1
(
)
(
/
k
n
c
c
c
n
c
c
c
n
n
c
c
c
c
n
c
n
c
c
c
c
c
c
n
v
v
p
v
p
v
p
v
v
v
p
Stąd:
1
)
(
n
k
n
c
c
v
Ciepło właściwe c może mieć wartość ujemną. Czynnik termodynamiczny ma ujemną
pojemność cieplną (ciepło właściwe) wówczas, gdy mimo doprowadzenia ciepła temperatura
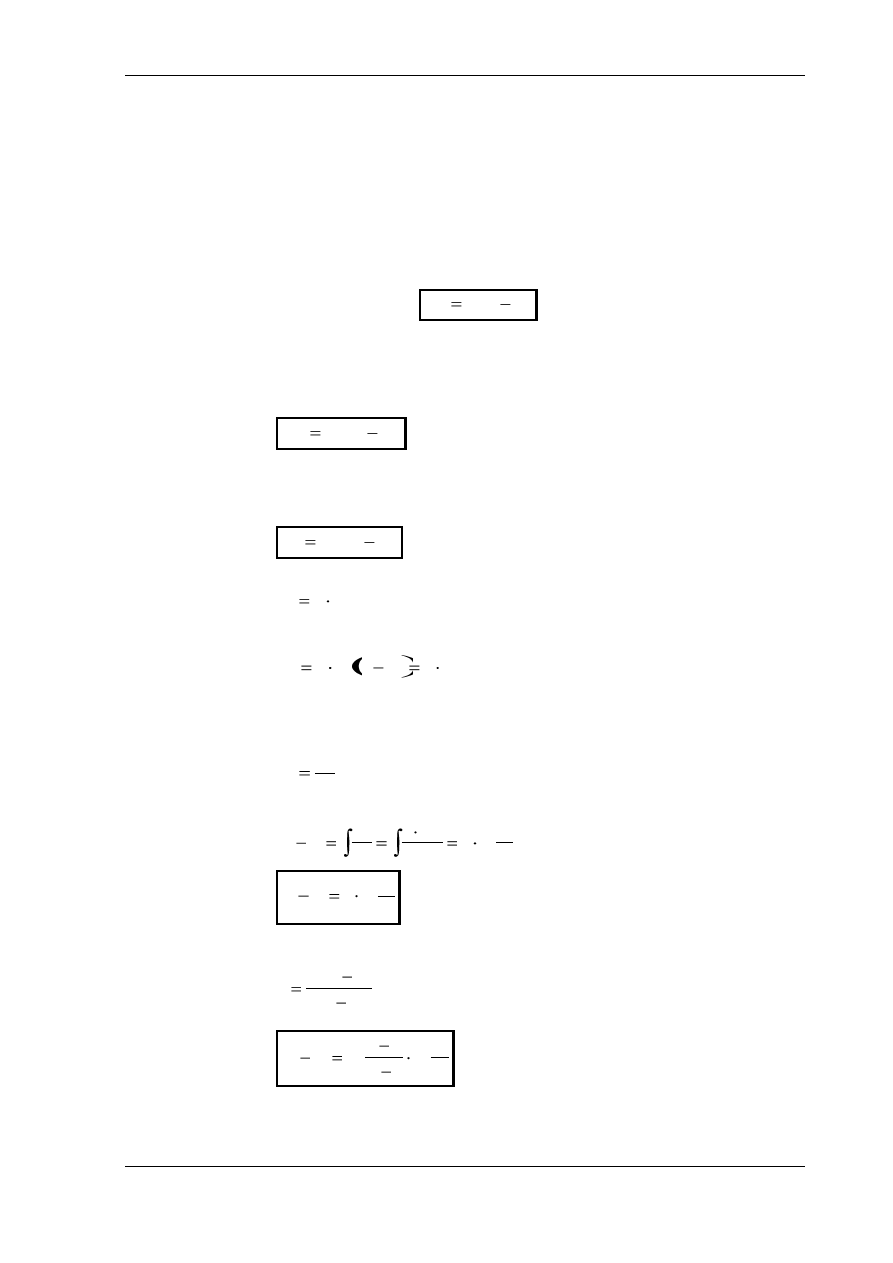
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
6
czynnika obniża się lub mimo odprowadzenia ciepła temperatura podwyższa się. Taka sytuacja
ma miejsce w sprężarkach – mimo odbierania ciepła temperatura gazu przy rozprężaniu
podwyższa się. W chłodzonych sprężarkach występuje więc przemiana o ujemnej pojemności
cieplnej.
CIEPŁO PRZEMIANY POLITROPOWEJ
)
(
1
2
2
,
1
T
T
c
q
ENERGIA WEWNĘTRZNA
Zgodnie z definicją:
)
(
1
2
2
,
1
T
T
c
u
v
ENTALPIA
Zgodnie z definicją:
)
(
1
2
2
,
1
T
T
c
i
p
Uwzględniając, że:
v
p
c
k
c
otrzymuje się:
2
,
1
1
2
2
,
1
u
k
T
T
c
k
i
v
ENTROPIA
Z definicji entropii:
T
dq
ds
Po scałkowaniu:
2
1
1
2
2
1
1
2
ln
T
T
c
T
dT
c
T
dq
s
s
1
2
1
2
ln
T
T
c
s
s
lub po podstawieniu:
1
)
(
n
k
n
c
c
v
o
trzymuje się:
1
2
1
2
ln
1
T
T
n
k
n
c
s
s
v
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
7
PRACA W PRZEMIANIE POLITROPOWEJ
UMOWA DOTYCZĄCA ZNAKU PRACY
wg: Bogumił Staniszewski „Termodynamika”, Stefan Wiśniewski „Termodynamika techniczna”,
Jan Szargut „Termodynamika”
Praca wykonana przez układ ma znak dodatni, wykonana zaś przez otoczenie nad
układem jest ujemna.
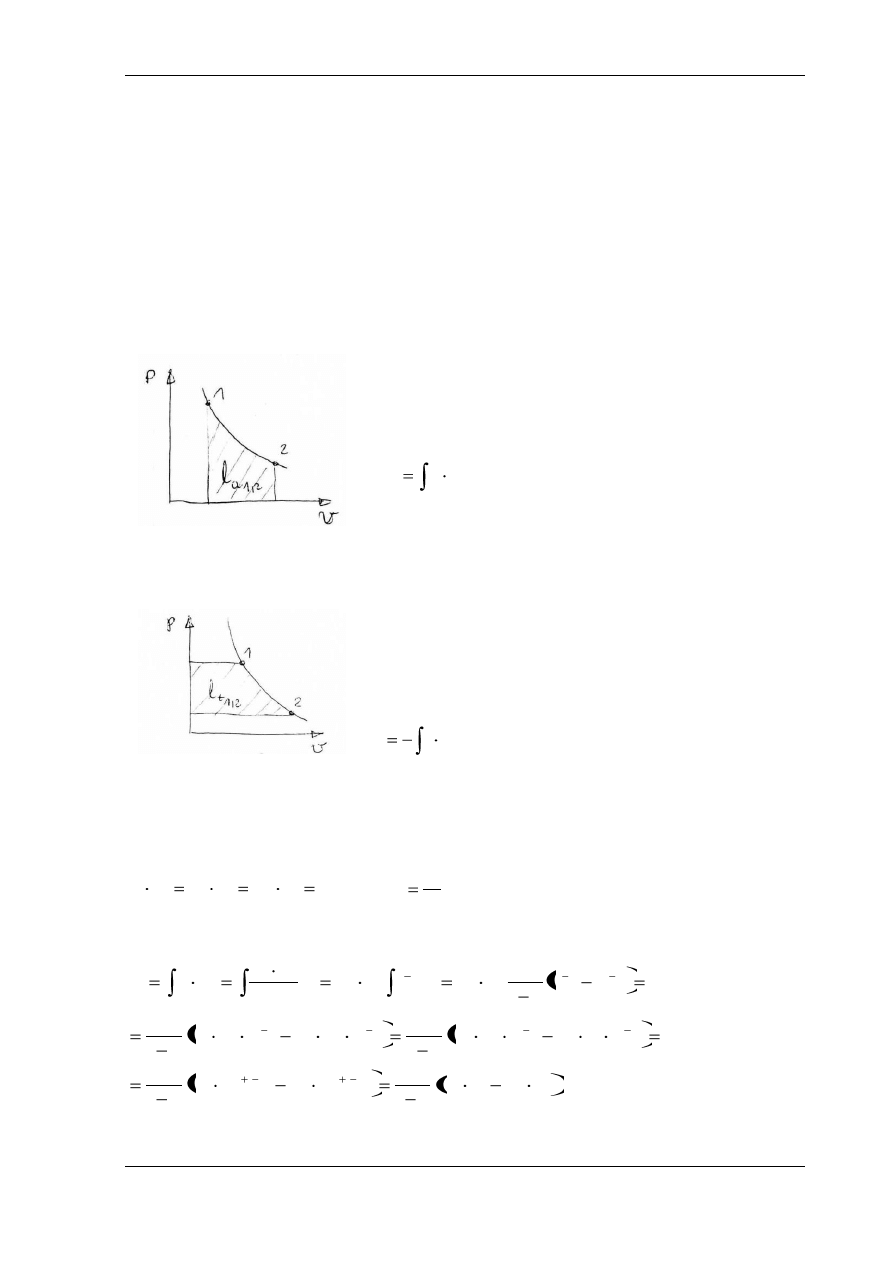
Praca absolutna
(praca zmiany objętości)
Praca zmiany objętości jest dodatnia podczas ekspansji
(zwiększania objętości) dv>0, a ujemna podczas kompresji
(zmniejszania objętości) dv<0.
2
1
2
,
1
dv
p
l
a
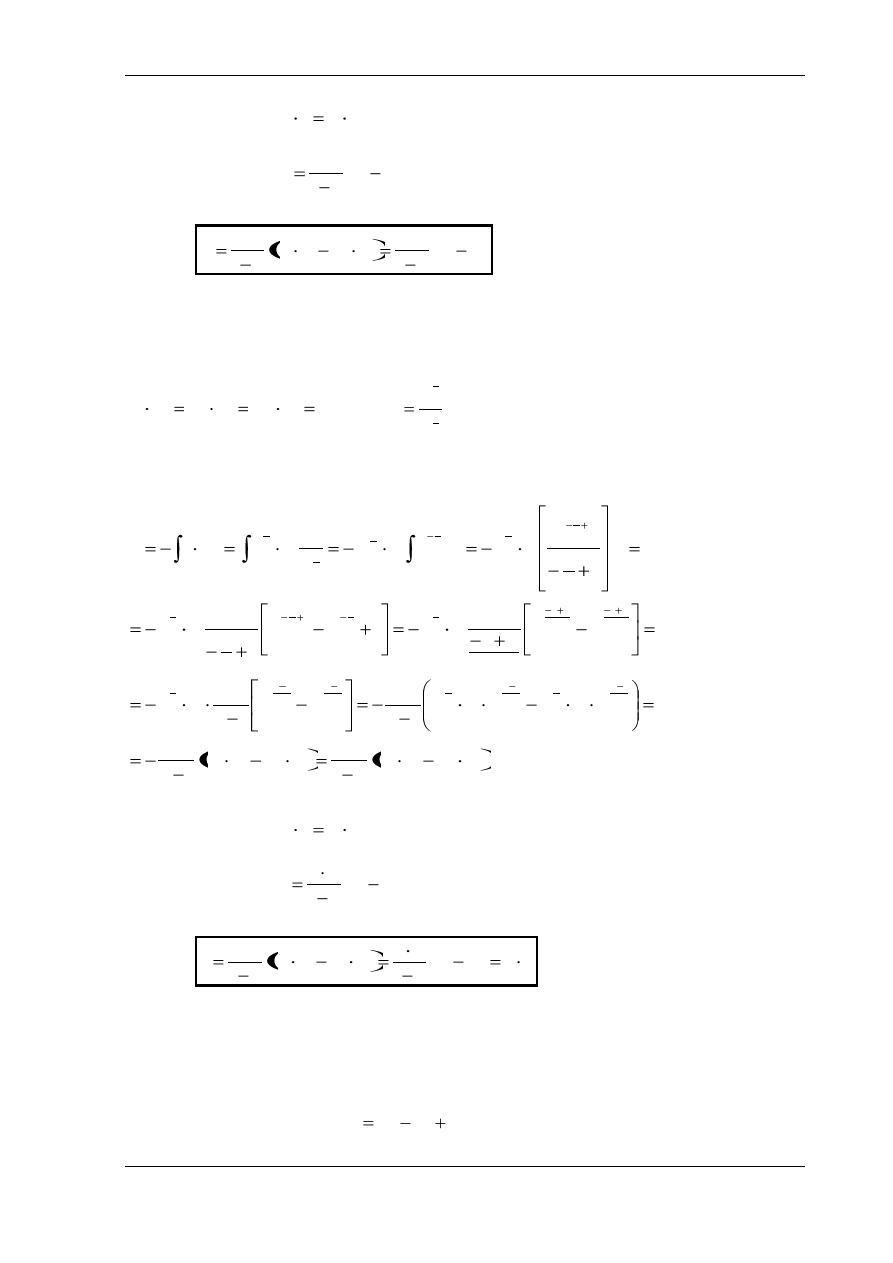
Praca techniczna
Pr
aca techniczna jest dodatnia przy rozprężaniu dp<0,
a
ujemna przy sprężaniu dp>0 (dlatego znak minus przed
całką).
2
1
dp
v
l
t
PRACA ABSOLUTNA
Równanie politropy:
....
2
2
1
1
n
n
n
v
p
v
p
v
p
stąd:
1
1
p
v
v
p
n
n
Praca absolutna:
lub po podstawieniu:
1
1
2
2
)
1
(
1
1
)
1
(
2
2
1
1
1
1
1
2
2
2
1
1
1
1
1
2
1
1
1
1
1
2
2
1
1
1
1
1
2
1
1
1
2
1
1
1
1
1
1
1
1
1
1
1
v
p
v
p
n
v
p
v
p
n
v
v
p
v
v
p
n
v
v
p
v
v
p
n
v
v
n
v
p
dv
v
v
p
dv
v
v
p
dv
p
l
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
8
T
R
v
p
otrzym
uje się:
)
(
1
1
2
T
T
n
R
l
a
A zatem:
)
(
1
1
1
1
2
1
1
2
2
T
T
n
R
v
p
v
p
n
l
a
PRACA TECHNICZNA
Równanie politropy:
....
2
2
1
1
n
n
n
v
p
v
p
v
p
stąd:
1
1
1
1
v
p
p
v
n
n
Praca techniczna:
lub po podstawieniu:
T
R
v
p
otrzym
uje się:
)
(
1
1
2
T
T
n
R
n
l
t
A zatem:
a
t
l
n
T
T
n
R
n
v
p
v
p
n
n
l
)
(
1
1
1
2
1
1
2
2
I. ZASADA TERMODYNAMIKI
-
dla układów zamkniętych:
2
,
1
1
2
2
,
1
A
L
U
U
Q
1
1
2
2
1
1
2
2
1
1
1
1
1
1
2
1
1
1
1
1
1
2
1
1
1
1
1
1
2
1
1
1
1
1
1
1
2
1
1
1
2
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
v
p
v
p
n
n
v
p
v
p
n
n
p
v
p
p
v
p
n
n
p
p
n
n
v
p
p
p
n
n
v
p
p
p
n
v
p
n
p
v
p
dp
p
v
p
p
dp
v
p
dp
v
l
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
p
p
n
n
n
n
n
n
t
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
9
albo:
2
,
1
2
,
1
2
,
1
A
L
Q
U
- dla
układów otwartych:
2
,
1
1
2
2
,
1
t
L
I
I
Q
albo:
2
,
1
2
,
1
2
,
1
t
L
Q
I
Wykres przemiany politropowej
(przykładowy)
Na rysunku poniżej jest przedstawiona przemiana politropowa o wykładniku 1<n<k
w
układzie współrzędnych p - v i T – s.
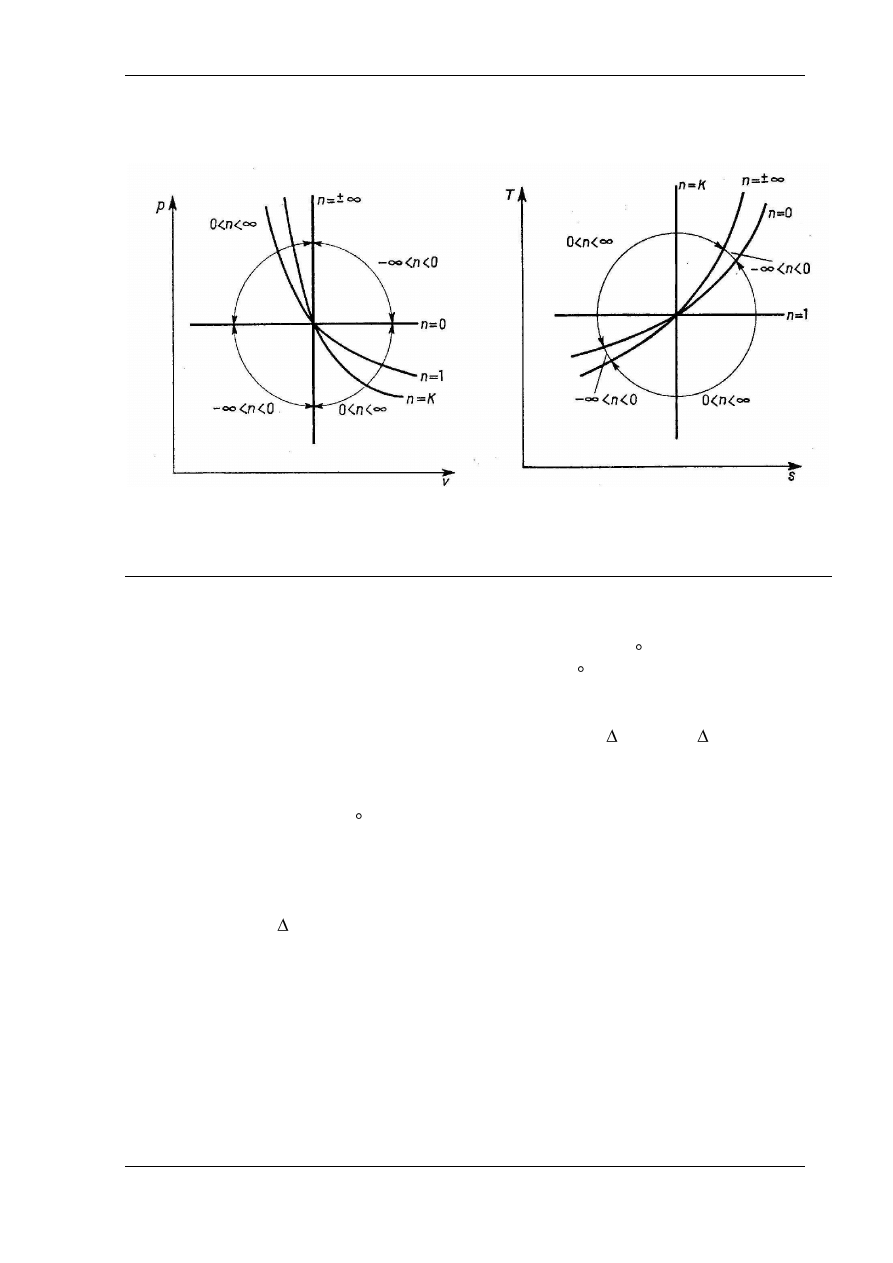
Przebieg przemiany politropowej
o wykładniku 1<n<k w układach: a) p – v, b) T – s
Na wykresie p
–v są oznaczone pola pracy absolutnej l
a1,2
(dodatniej, wykonanej przez gaz)
i pracy technicznej l
t1,2
(dodatniej), a na wykresie T
– s jest oznaczone pole ciepła przemiany
q
1,2
(dodatnie
– dostarczone z zewnątrz).
Na wykresie T
– s można również znaleźć:
- pole przyrostu
energii wewnętrznej – jest to pole pod logarytmiką v=const. przechodzącą
przez punkt
o wyższej energii wewnętrznej (w tym przykładzie jest to punkt 1 i logarytmika v
1
)
i
przecinającą izotermę przechodzącą przez punkt o niższej energii wewnętrznej (punkt 2
i izoterma T
2
)
– pole b,d,1,s
1
(w tym przykładzie – ujemny przyrost energii wewnętrznej),
- pole przyrostu entalpii -
jest to pole pod logarytmiką p=const. przechodzącą przez punkt
o
wyższej entalpii (w tym przykładzie jest to punkt 1 i logarytmika p
1
) i
przecinającą izotermę
przechodzącą przez punkt o niższej entalpii (punkt 2 i izoterma T
2
)
– pole a,c,1,s
1
(w tym
przykładzie – ujemny przyrost entalpii),
- po
le pracy absolutnej (w tym przykładzie wykonanej przez gaz – dodatniej) – pole b,d,1,2,s
2
),
- pole pracy technicznej (dodatniej)
– pole a,c,1,2,s
2
),
-
pole energii umieszczenia (energii przetłaczania) – pole a,c,1,d,b.
Przemiany gazu doskonałego
Opracowanie: Ewa Fudalej-Kostrzewa
10
Przebieg przemiany politropowej na wykresach p
– v i T – s zależy od wykładnika
politropy.
Przemiany politropowe na wykresie p
– v
Przemiany politropowe na wykresie T
– s
ZADANIA
ZADANIE 1
Powietrze o masie M=1,5 kg, ciśnieniu p
1
=0,9 bar, temperaturze t
1
=18 C zostało sprężone do
ciśnienia p
2
=10 bar, przy czym temperatura wzrosła do t
2
=125 C. Obliczyć wykładnik politropy,
objętość końcową, pracę absolutną i techniczną, ciepło przemiany oraz zmianę energii
wewnętrznej i entalpii. Stała gazowa powietrza: R=287 J/kg*K, k=c
p
/c
v
=14
Odp.: n=1,148, V
2
=0,171 m
3
, L
a
=-311 kJ, L
t
=-357 kJ, Q=-196 kJ, U=115 kJ, I=161,2 kJ
ZADANIE 2
Powietrze o temperaturze t
1
=20 C jest sprężane w sprężarce według politropy o wykładniku
n=1,2 od ciśnienia p
1
=0,1 MPa do ciśnienia p
2
=1 MPa. Obliczyć parametry końcowe przemiany,
pracę absolutną, pracę techniczną, ciepło właściwe, ciepło przemiany, zmianę entropii.
R=287 J/kg*K, k= c
p
/c
v
=1,4.
Odp.: T
2
=430 K, v
2
=0,123 m
3
/kg, l
a
=-196,6 kJ/kg, l
t
=-236 kJ/kg, c=-717,5 j/kg*K,
q=-98,3 kJ/kg, s=-275 J/kg*K