Statystyczne planowanie eksperymentu

1

StatGraph.lnk

PLANOWANIE EKSPERYMENTU
1. INFORMACJE WST

Ę

PNE

Planowanie eksperymentu

(PE) ang. The Design of Experiments

⇒

R.A. Fisher 1935 rok (w ramach prac dotycz

ą

cych analizy

wariancyjnej).

Eksperyment

- seria do

ś

wiadcze

ń

, np. w metalurgii seria wytopów

stali o ró

ż

nych składach chemicznych.

Cel planowania eksperymentu

- wyznaczenie opisu

matematycznego obiektu bada

ń

lub zjawiska, tzw. modelu

matematycznego, umo

ż

liwiaj

ą

cego analiz

ę

jego zachowania i ustalenia

czynników wpływaj

ą

cych na zachowanie obiektu.

Statystyczne planowanie eksperymentu

2

StatGraph.lnk

2. WYBÓR CZYNNIKÓW I ZMIENNYCH STANU OBIEKTU BADA

Ń

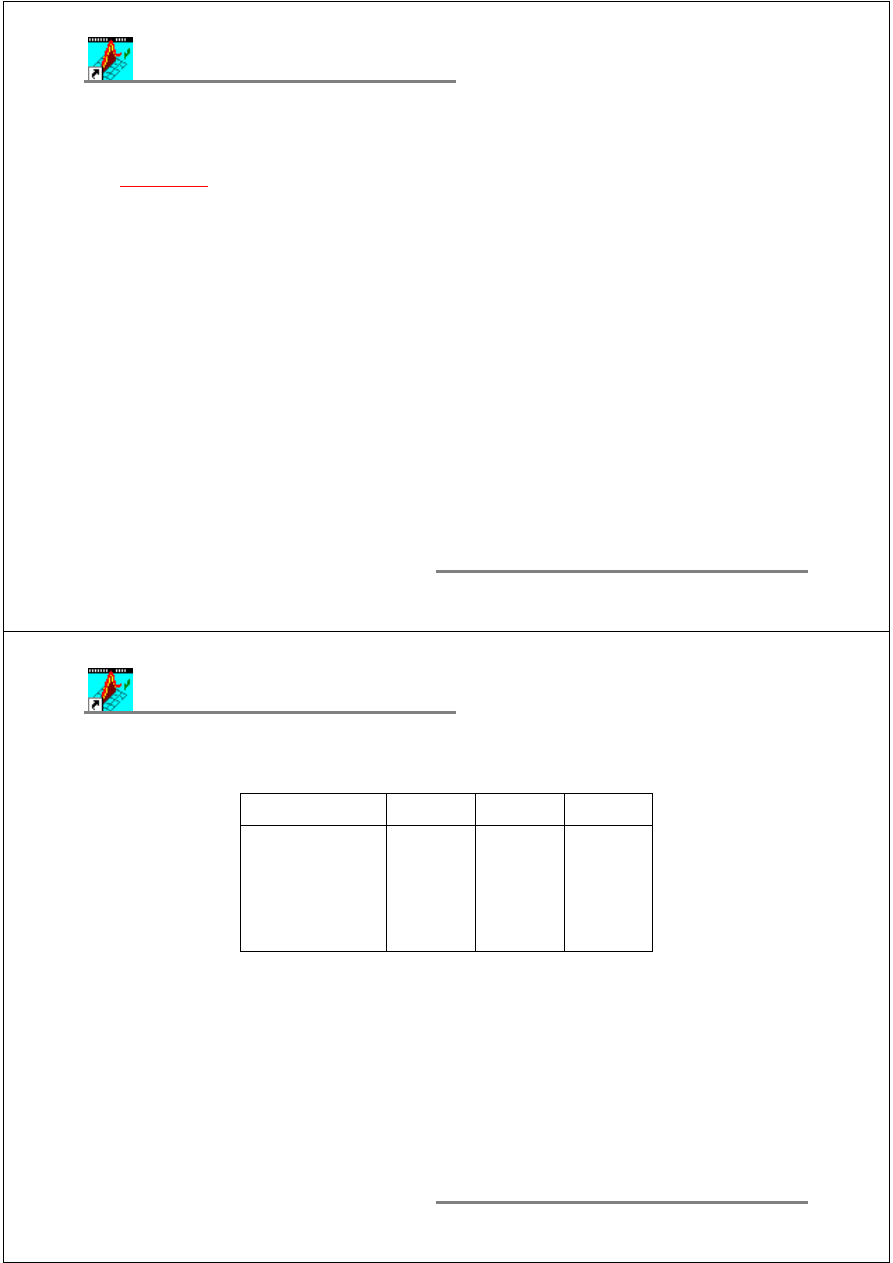
Obiekt bada

ń

mo

ż

na przedstawi

ć

jako czarn

ą

skrzynk

ę

:

Gdzie:

x

1

, x

2

, ...,x

n

- zmienne wej

ś

ciowe (czynniki)

y

1

, y

2

, ...,y

m

- zmienne wyj

ś

ciowe, charakteryzuj

ą

ce stan obiektu

w zale

ż

no

ś

ci od zmiennych wej

ś

ciowych - nazywane równie

ż

zmiennymi stanu

z

-

zmienna przypadkowa o nieokre

ś

lonym rozkładzie,

niekontrolowana (zakłócenie)

Obiekt

z

x

1

x

2

x

n

y

1

y

2

y

m

Statystyczne planowanie eksperymentu

3

StatGraph.lnk

3. RÓ

Ż

NICA MI

Ę

DZY ZWYKŁYM I STATYSTYCZNYM

PLANOWANIEM EKSPERYMENTU

Wg metody planowania zwykłego zmienne zmienia si

ę

stopniowo,

przy czym wszystkie pozostałe zmienne utrzymuje si

ę

stałe. Nast

ę

pnie

zmienia si

ę

kolejn

ą

zmienn

ą

, a pozostałe utrzymuje si

ę

stałe itd.

Otrzymuje si

ę

w ten sposób wyniki bada

ń

jako zale

ż

no

ś

ci zmiennej

stanu od ka

ż

dej zmiennej przy ustalonym poziomie wszystkich

pozostałych zmiennych (np. w postaci krzywej). Potrzebna liczba bada

ń

jest du

ż

a.

W statystycznym planowaniu eksperymentu dokonuje si

ę

zmiany

jednocze

ś

nie

wszystkich zmiennych w planie eksperymentu.

Statystyczne planowanie eksperymentu

4

StatGraph.lnk

4. EKSPERYMENT WST

Ę

PNY I EKSPERYMENT PODSTAWOWY

Eksperyment wst

ę

pny

przeprowadza si

ę

w przypadku, gdy brak

jakiejkolwiek informacji o obiekcie bada

ń

. Jego celem jest uzyskanie

wst

ę

pnych informacji o obiekcie niezb

ę

dnych do przeprowadzenia

eksperymentu podstawowego.

Zadaniem

eksperymentu podstawowego

jest uzyskanie modelu

badanego obiektu, który wykorzystuje si

ę

dla optymalizacji obiektu (lub

procesu) lub jako opis matematyczny słu

żą

cy do badania jego

zachowania.

Statystyczne planowanie eksperymentu

5

StatGraph.lnk

5. EKSPERYMENT CZYNNIKOWY. PLANY RZ

Ę

DU PIERWSZEGO

Przykład

Obiektem badania jest aparatura wytwarzaj

ą

ca pewn

ą

ilo

ść

produktu y. Ilo

ść

wyprodukowanego produktu zale

ż

y od temperatury x

1

i ci

ś

nienia x

2

panuj

ą

cych w aparacie. Oznaczmy maksymalne i

minimalne warto

ś

ci czynników x

1

i x

2

przez +1 i -1. Wówczas wszystkie

mo

ż

liwe kombinacje czynników przy wariowaniu na dwóch poziomach

(minimalnym i maksymalnym) b

ę

d

ą

okre

ś

lone w czterech

do

ś

wiadczeniach. Taki plan eksperymentu przyj

ę

to zapisywa

ć

w

postaci macierzy planowania:

Statystyczne planowanie eksperymentu

6

StatGraph.lnk

Do

ś

w. nr

x

1

x

2

y

1

+1

+1

y

1

2

-1

+1

y

2

3

+1

-1

y

3

4

-1

-1

y

4

W tym przypadku mamy

Liczba poziomów - 2
Liczna czynników k=2
Liczba do

ś

wiadcze

ń

w eksperymencie N=2

k

= 2

2

Statystyczne planowanie eksperymentu

7

StatGraph.lnk

BUDOWA MACIERZY PLANOWANIA

Plan eksperymentu, zawieraj

ą

cy zapis

wszystkich

kombinacji

czynników albo ich

cz

ęś

ci

nazywa si

ę

macierz

ą

planowania. W

budowie macierzy planowania dla du

ż

ej liczby czynników stosuje si

ę

szereg ró

ż

nych metod

Statystyczne planowanie eksperymentu

8

StatGraph.lnk

L.p.

x

1

x

2

x

3

x

4

1

+1

+1

+1

+1

2

-1

+1

+1

+1

3

+1

-1

+1

+1

4

-1

-1

+1

+1

5

+1

+1

-1

+1

6

-1

+1

-1

+1

7

+1

-1

-1

+1

8

-1

-1

-1

+1

9

+1

+1

+1

-1

10

-1

+1

+1

-1

11

+1

-1

+1

-1

12

-1

-1

+1

-1

13

+1

+1

-1

-1

14

-1

+1

-1

-1

15

+1

-1

-1

-1

16

-1

-1

-1

-1

Statystyczne planowanie eksperymentu

9

StatGraph.lnk

WŁASNO

Ś

CI MACIERZY PLANOWANIA

Macierze planowania posiadaj

ą

własno

ś

ci zwi

ą

zane z

optymalno

ś

ci

ą

modelu, do którego wyznaczenia słu

żą

.

Symetryczno

ść

:

∑

=

=

N

k

ik

x

1

0

i=1, 2, ...,n - czynniki

Unormowanie:

∑

=

=

N

k

ik

N

x

1

2

- ilo

ść

do

ś

wiadcze

ń

gdzie: i - numer czynnika

k - numer do

ś

wiadczenia

Statystyczne planowanie eksperymentu

10

StatGraph.lnk

Warunek ortogonalno

ś

ci

zakłada równo

ść

zeru sumy iloczynów

elementów dowolnych dwóch kolumn macierzy planowania:

∑

=

=

N

k

jk

ik

x

x

1

0

(i,j = 1,2,....., n, i

≠

j)

Statystyczne planowanie eksperymentu

11

StatGraph.lnk

6. PLANY 2

3

Pełny plan czynnikowy pozwala uwzgl

ę

dni

ć

wzajemne

oddziaływania czynników. W tym celu plan eksperymentu uzupełnia si

ę

kolumnami, przedstawiaj

ą

cymi iloczyny odpowiednich kolumn

czynników.

Dla pełnego eksperymentu czynnikowego 2

3

macierz planowania

eksperymentu z udziałem efektów oddziaływania przedstawia si

ę

nast

ę

puj

ą

co:

Statystyczne planowanie eksperymentu

12

StatGraph.lnk

Do

ś

w.

nr

x

1

x

2

x

3

x

1

x

2

x

1

x

3

x

2

x

3

y

1

+

+

+

+

+

+

y

1

2

-

+

+

-

-

+

y

2

3

+

-

+

-

+

-

y

3

4

-

-

+

+

-

-

y

4

5

+

+

-

+

-

-

y

5

6

-

+

-

-

+

-

y

6

7

+

-

-

-

-

+

y

7

8

-

-

-

+

+

+

y

8

Statystyczne planowanie eksperymentu

13

StatGraph.lnk

Współczynniki b

ij

oblicza si

ę

z wzoru:

∑

=

=

N

k

k

jk

ik

ij

y

x

x

N

b

1

1

(i

≠

j)

W ten sposób mo

ż

na otrzyma

ć

model matematyczny postaci:

∑

∑

=

=

+

+

=

n

j

i

j

i

j

i

n

i

i

i

x

x

b

x

b

b

y

1

,

,

1

0

ˆ

I tak dla planu 2

2

:

2

1

12

2

2

1

1

0

ˆ

x

x

b

x

b

x

b

b

y

+

+

+

=

Statystyczne planowanie eksperymentu

14

StatGraph.lnk

Zwi

ę

kszenie liczby czynników prowadzi do szybkiego zwi

ę

kszenia

liczby do

ś

wiadcze

ń

, np. przy 6 czynnikach liczba do

ś

wiadcze

ń

wynosi

2

6

=64, a przy 7 2

7

=128.

W praktyce, dla otrzymania dokładnych ocen współczynników

równania regresji wystarcza przeprowadzenie niedu

ż

ej liczby

do

ś

wiadcze

ń

. Dlatego te

ż

dla du

ż

ej liczby czynników wprowadza si

ę

tzw.

ułamkowy eksperyment (plan) czynnikowy

, nazywany równie

ż

planem cz

ęś

ciowym, powtarzaniem ułamkowym, replik

ą

ułamkow

ą

.

Stanowi on pewn

ą

cz

ęść

(np. 1/2, 1/4, 1/8 itd.) Pełnego Eksperymentu

Czynnikowego (PECZ)

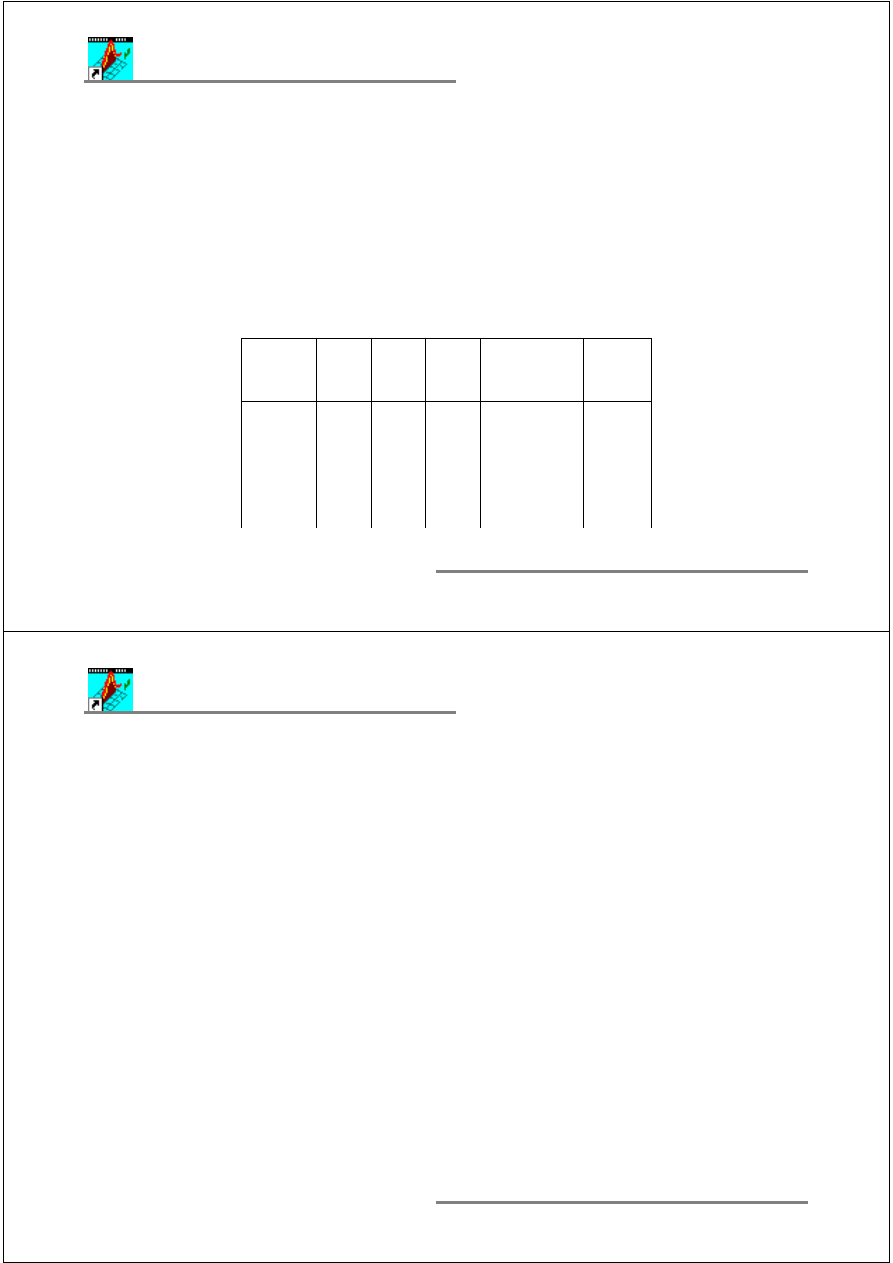
Statystyczne planowanie eksperymentu

15

StatGraph.lnk

Przykład

Załó

ż

my,

ż

e trzeba opisa

ć

pewn

ą

cz

ęść

funkcji celu (zmiennej

stanu) od trzech zmiennych niezale

ż

nych równaniem liniowym.

W tym celu mo

ż

na wykorzysta

ć

plan typu

2

3

z 8 do

ś

wiadczeniami,

ograniczaj

ą

c si

ę

do 1/2 tego planu tj. do 4 do

ś

wiadcze

ń

. W tym celu

kolumn

ę

oddziaływa

ń

x

1

x

2

PECZ 2

2

przypisujemy czynnikowi trzeciemu

x

3

.

Do

ś

w.

nr

x

0

x

1

x

2

x

3

=x

1

x

2

y

1

+

+

+

+

y

1

2

+

-

+

-

y

2

3

+

+

-

-

y

3

4

+

-

-

+

y

4

Statystyczne planowanie eksperymentu

16

StatGraph.lnk

Repliki, w których

p

efektów liniowych jest przyrównywane do

efektów oddziaływa

ń

umownie oznacza si

ę

2

n-p

.

W ten sposób półreplik

ę

od PECZ

2

6

b

ę

dziemy zapisywa

ć

2

6-1

.

Statystyczne planowanie eksperymentu

17

StatGraph.lnk

Liczba

czynników

Replika

ułamkowa

Oznaczenie Ilo

ść

do

ś

w. Ilo

ść

do

ś

w.

PECZ

3

1/2 od 2

3

2

3-1

4

8

4

1/2 od 2

4

2

4-1

8

16

5

1/4 od 2

5

2

5-2

8

32

6

1/8 od 2

6

2

6-3

8

64

7

1/16 od 2

7

2

7-4

8

128

5

1/2 od 2

5

2

5-1

16

32

6

1/4 od 2

6

2

6-2

16

64

7

1/8 od 2

7

2

7-3

16

128

8

1/16 od 2

8

2

8-4

16

256

9

1/32 od 2

9

2

9-5

16

512

10

1/64 od 2

10

2

10-6

16

1024

Statystyczne planowanie eksperymentu

18

StatGraph.lnk

7.

PLANY RZ

Ę

DU DRUGIEGO

Wymaganie adekwatno

ś

ci modelu w obszarze eksperymentu

powoduje,

ż

e mo

ż

e bardzo cz

ę

sto musi on by

ć

nieliniowy, np.:

∑

∑

∑

=

=

+

+

+

=

≠

=

n

i

i

ii

n

i

n

j

i

ij

i

i

x

a

x

x

a

x

a

a

y

j

i

j

i

1

2

1

0

1

,

ˆ

Przy pomocy dotychczas omówionych metod nie da si

ę

zbudowa

ć

takiego modelu, gdy

ż

nie jest spełniony warunek ortogonalno

ś

ci w

kolumnach x

i

2

(suma elementów b

ę

dzie równa

N

, a nie

0

).

Dla otrzymania modelu o takiej postaci stosuje si

ę

plany specjalne.

Statystyczne planowanie eksperymentu

19

StatGraph.lnk

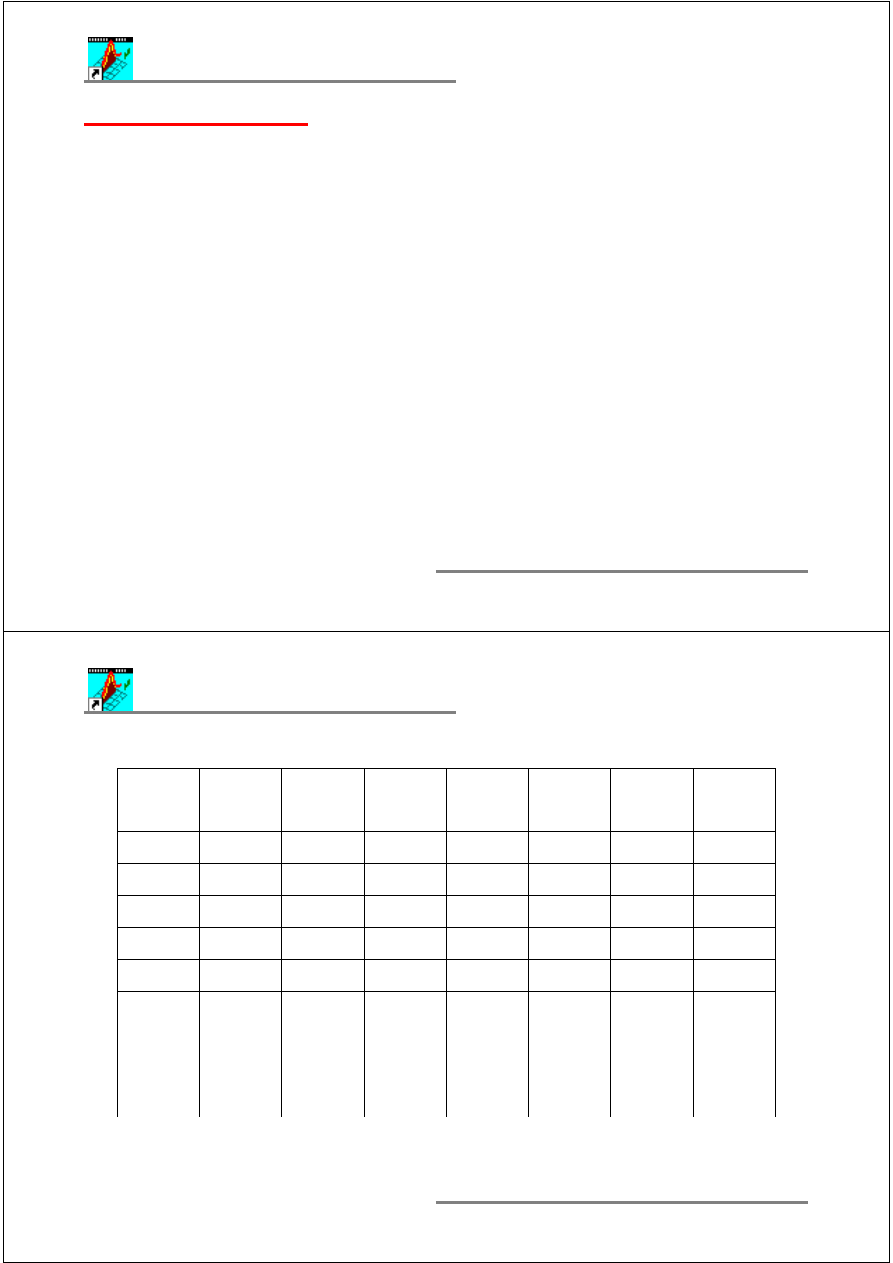
Do

ś

w. nr

x

1

x

2

y

1

+

+

y

1

2

+

-

y

2

3

+

0

y

3

4

-

+

y

4

5

-

-

y

5

6

-

0

y

6

7

0

+

y

7

8

0

-

y

8

9

0

0

y

9

Statystyczne planowanie eksperymentu

20

StatGraph.lnk

Wybór liczby poziomów

Model matematyczny w postaci wielomianu rz

ę

du drugiego wymaga

zastosowania trzech poziomów czynników –

3

n

.

W przypadku liczby czynników wi

ę

kszej od 4, pełny eksperyment

czynnikowy na 3-ch poziomach jest nieekonomiczny (3

4

– N=81, 3

5

–

N=243).

Statystyczne planowanie eksperymentu

21

StatGraph.lnk

Plany kompozycyjne

Je

ż

eli plan PECZ uzupełnimy okre

ś

lonymi (konkretnymi) punktami

przestrzeni czynnikowej, mo

ż

na otrzyma

ć

plan o mniejszej liczbie

do

ś

wiadcze

ń

ni

ż

plan typu 3

n

.

Ogóln

ą

liczb

ę

do

ś

wiadcze

ń

przy takim planowaniu okre

ś

la si

ę

z

zale

ż

no

ś

ci:

N=2

n

+2n+N

0

Gdzie poszczególne składniki okre

ś

laj

ą

odpowiednio liczb

ę

do

ś

wiadcze

ń

w PECZ typu 2

n

, punktów dodatkowych (tzw. gwiezdnych)

i punktów zerowych.

Statystyczne planowanie eksperymentu

22

StatGraph.lnk

Plan kompozycyjny typu 2

2

Do

ś

w.

nr

x

0

x

1

x

2

x

1

x

2

x

1

2

x

2

2

y

1

+1

+1

+1

+1

+1

+1

y

1

2

+1

+1

-1

-1

+1

+1

y

2

3

+1

-1

+1

-1

+1

+1

y

3

4

+1

-1

-1

+1

+1

+1

y

4

5

+1

+a

0

0

a

2

0

y

5

6

+1

-a

0

0

a

2

0

y

6

7

+1

0

+a

0

0

a

2

y

7

8

+1

0

-a

0

0

a

2

y

8

9

+1

0

0

0

0

0

y

9

Wybór punktów gwiezdnych i liczba punktów zerowych zale

ż

y od

przyj

ę

tego kryterium optymalno

ś

ci.