1

Informatyka i Komputerowe Wspomaganie
Prac In

ż

ynierskich

Modelowanie – cz. 1 „Podstawy modelowania matematycznego”

2

Rozumienie rzeczywisto

ś

ci na modelach

W naukach technicznych

rozumienie

pojmowane jest jako poj

ę

ciowe

wychwycenie odpowiednio

ś

ci

mi

ę

dzy obiektami i zjawiskami

naturalnymi a obiektami teoretycznymi (tworami abstrakcyjnymi), czyli

okre

ś

lenie poj

ęć

i relacji

, które zwi

ą

zane s

ą

z okre

ś

lonymi cechami

obiektów i procesów materialnych.

Dokonuje si

ę

tego na

modelach

.

Model

jest uproszczeniem (abstrakcj

ą

) istniej

ą

cych obiektów, procesów

i zjawisk rzeczywistych; jest celowo dobranym układem cech
przedmiotów poddanych badaniu.

W działaniach technicznych szczególn

ą

umiej

ę

tno

ś

ci

ą

jest

przechodzenie ze sfery

konkretów

do

abstrakcji

(i odwrotnie).

3

Istota modelowania

Modelowanie

jest jedn

ą

z podstawowych metod badawczych.

Modelowanie

polega na korzystaniu z zale

ż

no

ś

ci i wnioskowa

ń

prowadzonych przy u

ż

yciu aparatu logicznego i formalizmu

matematycznego, czego wynikiem s

ą

np. przewidywania co do

pewnych cech i zachowa

ń

rozpatrywanego obiektu.

Modelowanie

to nie tyko otrzymanie konkretnego modelu, lecz cały cykl

badawczy, od utworzenia modelu poczynaj

ą

c, przez jego weryfikacj

ę

,

interpretacje, a ko

ń

cz

ą

c na kolejnym przybli

ż

eniu.

4

Korzy

ś

ci wynikaj

ą

ce z modelowania

1.

Modele daj

ą

podstaw

ę

do symulacji, czyli wirtualnego badania i

przekształcania rzeczywisto

ś

ci.

2.

Modele pozwalaj

ą

na okre

ś

lanie zwi

ą

zków pomi

ę

dzy parametrami

symptomów diagnostycznych i cechami stanu obiektu
technicznego.

3.

Techniki modelowania i symulacji prowadz

ą

do redukcji kosztów i

czasu w projektowaniu nowych procesów i wyrobów.

4.

Modele pozwalaj

ą

przewidywa

ć

własno

ś

ci nowych materiałów.

5

Klasyfikacja modeli

Z punktu widzenia spełnianych

funkcji

mo

ż

na wyró

ż

ni

ć

3 grupy modeli:

Modele strukturalne

– pokazuj

ą

ce powi

ą

zania i lokalizacj

ę

geometryczn

ą

wyró

ż

nionych elementów, wygodne do analizy organizacji obiektu i

zagadnie

ń

zwi

ą

zanych z kierowaniem i sterowaniem obiektem. Modele te

maj

ą

zwykle posta

ć

: relacji logicznych (powi

ą

zania strzałkowe), opisowo-

graficzn

ą

, np. schemat organizacyjny, lub posta

ć

zło

ż

eniowego rysunku

technicznego.

Modele funkcjonalne

– pokazuj

ą

ce wpływ ró

ż

nych elementów obiektu na

poszczególne funkcje (zadania) wykonywane przez obiekt, np.: modele
opisowo-graficzne, schematy blokowe itp.

Modele badawcze

– w

ś

ród których wyró

ż

nia si

ę

:

modele ideowe

– pokazuj

ą

ce sposób realizacji okre

ś

lonych zada

ń

, np. schematy

elektryczne,

modele analityczne

– umo

ż

liwiaj

ą

ce ilo

ś

ciowe okre

ś

lanie wła

ś

ciwo

ś

ci obiektu. Maj

ą

one zwykle posta

ć

matematyczn

ą

, np. zale

ż

no

ś

ci funkcyjne, macierze, opisy

procesów itp.

6

Klasyfikacja modeli

Z punktu widzenia sposobu odtwarzania rzeczywisto

ś

ci wyró

ż

nia si

ę

dwie grupy modeli

- modele materialne:

istniej

ą

w rzeczywisto

ś

ci, funkcjonuj

ą

wg praw

przyrody (i w tym sensie s

ą

niezale

ż

ne od człowieka).

- modele abstrakcyjne (my

ś

lowe):

istniej

ą

jedynie w

ś

wiadomo

ś

ci

człowieka; mog

ą

odtwarza

ć

te same zjawiska, co modele materialne;

mimo,

ż

e mog

ą

by

ć

wyra

ż

one np. jako rysunki, szkice lub znaki,

funkcjonuj

ą

jedynie dzi

ę

ki operacjom my

ś

lowym.

7

Konstruowanie modeli

W technice i nauce najbardziej poszukiwanymi modelami s

ą

modele

matematyczne

. Stanowi

ą

one najbardziej reprezentatywn

ą

grup

ę

modeli

my

ś

lowych. Modelowanie matematyczne pozwala wnika

ć

w istot

ę

badanych

systemów i udost

ę

pnia szczegółowemu badaniu wiele własno

ś

ci, procesów i

zwi

ą

zków.

Buduj

ą

c model konieczne jest okre

ś

lenie :

1.

Listy zjawisk i procesów

jakie wyst

ę

puj

ą

w badanym układzie (obiekcie) –

zmienne i parametry.

2.

Listy zało

ż

e

ń

, które wprost powinny wynika

ć

z po

żą

danego zakresu

wa

ż

no

ś

ci modelu (a ten jest dany lub przyj

ę

ty).

3.

Listy uproszcze

ń

, która wynika: z zało

ż

e

ń

i po

żą

danego zakresu bada

ń

oraz

potrzebnej (

żą

danej) dokładno

ś

ci analizy.

8

Etapy modelowania matematycznego

Pomi

ę

dzy poszczególnymi etapami modelowania wyst

ę

puj

ą

interakcje –

proces modelowania nie jest procesem o szeregowej strukturze

•

Sformułowanie celów i zało

ż

e

ń

modelowania

•

Budowa bazy wiedzy i bazy danych o modelowanym systemie

•

Wybór kategorii modelu

•

Okre

ś

lenie struktury modelu; budowa modelu

•

Identyfikacja modelu

•

Algorytmizacja modelu

•

Weryfikacja modelu

9

Zastosowanie

Sprz

ęż

enia pomi

ę

dzy etapami budowy modelu matematycznego

Problem rozwi

ą

zywany z pomoc

ą

modelowania matematycznego

Cele i zało

ż

enia modelowania

Baza wiedzy

Baza danych

♦

Teorie

♦

Prawa

♦

Wiedza

empiryczna

♦

Hipotezy

♦

Dane

eksperymentalne

♦

Kategoria modelu

♦

Struktura modelu

♦

Identyfikacja modelu

♦

Algorytmizacja modelu

♦

Weryfikacja modelu

Model zweryfikowany

10

Metodologia pozyskiwania wiedzy naukowej

11

Dlaczego jasne okre

ś

lenie celu modelowania jest wa

ż

ne?

1.

ma to bezpo

ś

redni wpływ na przebieg procesu modelowania –

ró

ż

ne cele implikuj

ą

ró

ż

ne problemy jakie trzeba rozwi

ą

za

ć

przy

modelowaniu;

2.

modelowanie jest najcz

ęś

ciej działalno

ś

ci

ą

interdyscyplinarn

ą

–

okre

ś

lenie celu musi by

ć

jasne dla wszystkich bior

ą

cych udział w

modelowaniu;

3.

po zbudowaniu modelu nale

ż

y oceni

ć

, na ile zadowalaj

ą

co

postawiony cel został osi

ą

gni

ę

ty.

Okre

ś

lenie celów modelowania

12

Cele ogólne modelowania

♦

Opis i wyja

ś

nienie mechanizmów działania systemu

–

model poznawczy

♦

Przewidywanie zachowania si

ę

systemu przy ró

ż

norodnych warunkach

oddziaływania otoczenia na system

–

model prognostyczny, predykcyjny

♦

Wybór odpowiednich oddziaływa

ń

wej

ś

ciowych, spełniaj

ą

cych

okre

ś

lone warunki i zapewniaj

ą

cych po

żą

dane reakcje wyj

ś

ciowe

–

model decyzyjny, wyznaczania sterowa

ń

•

w szczególno

ś

ci wybór oddziaływa

ń

optymalnych w sensie

wybranego kryterium

-

model optymalizacyjny

♦

Wybór struktury lub parametrów systemu maj

ą

cego spełnia

ć

okre

ś

lone

zadania

–

model projektowy, normatywny

13

Zało

ż

enia modelu

♣

Granice pomi

ę

dzy systemem a otoczeniem, zmienne wej

ś

ciowe i

wyj

ś

ciowe, ....

♣

Skala czasowa modelu, ....

♣

Dokładno

ść

zgodno

ś

ci modelu systemu z systemem rzeczywistym, ....

♣

Warunki stosowalno

ś

ci modelu, ....

14

Wiedza a’priori

•

Do

ś

wiadczenie

•

Istniej

ą

ce modele

•

Literatura (fakty, zjawiska, teorie, ...)

Dane

•

Istniej

ą

ce dane

•

Nowe dane zbierane dla celów budowy modelu

Ź

rodła informacji o modelowanym systemie

15

♦

NIEPARAMETRYCZNE lub PARAMETRYCZNE

Modele nieparametryczne

systemu to modele dane w postaci

wykresu, funkcji itp., które niekonieczne opisane by

ć

mog

ą

za

pomoc

ą

sko

ń

czonej liczby parametrów (danych):

charakterystyki czasowe elementu – modelem jest sygnał wyj

ś

ciowy wywołany

odpowiednim sygnałem wej

ś

ciowym;

charakterystyka cz

ę

stotliwo

ś

ciowe elementu liniowego –

modelem jest

zale

ż

no

ść

amplitudy

i

fazy

sygnału

wyj

ś

ciowego

od

cz

ę

stotliwo

ś

ci

sinusoidalnego sygnału wej

ś

ciowego;

Modele parametryczne

systemu to modele w których dla pełnego

opisu elementu potrzebna jest znajomo

ść

na pewno sko

ń

czonej

liczby parametrów (współczynników):

równania algebraiczne

Kategorie modeli (matematycznych)

16

♦

FENOMENOLOGICZNE (white – box) lub BEHAWIORALNE (black-box)

Modele fenomenologiczne

(lub oparte o wiedz

ę

):

Struktura modelu pozostaje w zasadniczym zwi

ą

zku ze struktur

ą

procesów a

parametry modelu posiadaj

ą

fizykaln

ą

interpretacj

ę

Modele behawioralne

- modele budowane w oparciu o zebrane dane

pomiarowe, modele które jedynie aproksymuj

ą

obserwowane

zachowanie si

ę

systemu, nie wymagaj

ą

c w tym celu

ż

adnej wiedzy a

priori o procesach generuj

ą

cych te dane

Struktura modelu nie musi pozostawa

ć

w

ż

adnym zasadniczym zwi

ą

zku ze

struktur

ą

procesów a parametry nie posiadaj

ą ż

adnej fizykalnej interpretacji

Kategorie modeli (matematycznych)

17

♦

STATYCZNE lub DYNAMICZNE

Statyczne

dotycz

ą

systemów statycznych

składaj

ą

cych si

ę

z

elementów zdolnych co najwy

ż

ej przekazywa

ć

energi

ę

, mas

ę

,

informacj

ę

bez strat lub ze stratami – daj

ą

si

ę

opisywa

ć

m.in. za

pomoc

ą

układów równa

ń

algebraicznych – ci

ą

głych lub dyskretnych

Dynamiczne

dotycz

ą

systemów

dynamicznych

zawieraj

ą

cych

elementy zdolne gromadzi

ć

i oddawa

ć

energi

ę

, mas

ę

, informacj

ę

–

mog

ą

by

ć

opisywane m.in. za

pomoc

ą

układów równa

ń

ró

ż

niczkowych lub ró

ż

nicowych

Je

ż

eli istotne s

ą

jedynie stany równowagi systemu dynamicznego, w których

dany system mo

ż

e si

ę

znajdowa

ć

, to mo

ż

na ograniczy

ć

si

ę

dla takiego

systemu dynamicznego do modelu statycznego

Kategorie modeli (matematycznych)

18

♦

LINIOWE lub NIELINIOWE

Rozró

ż

nia si

ę

dwa rodzaje liniowo

ś

ci:

liniowo

ść

wzgl

ę

dem wej

ść

(LI - linear in its inputs),

liniowo

ść

wzgl

ę

dem parametrów (LP – linear in its parameters)

Kategorie modeli (matematycznych)

Niech

(

)

u

p,

,

t

y

m

b

ę

dzie w chwili

t

wyj

ś

ciem modelu o parametrach

p

, je

ż

eli wej

ś

cie

zostało podane przy zerowych warunkach pocz

ą

tkowych (brak innych

oddziaływa

ń

na obiekt)

( )

t

0

,

≤

τ

≤

τ

u

19

♦

LINIOWE lub NIELINIOWE

Struktura modelu jest

liniowa wzgl

ę

dem wej

ść

(LI) je

ż

eli jego wyj

ś

cie

spełnia warunek liniowo

ś

ci wzgl

ę

dem jego wej

ść

, t.j.

Kategorie modeli (matematycznych)

(

)

(

)

(

)

(

)

2

m

2

1

m

1

2

2

1

1

m

2

2

1

,

,

t

,

,

t

,

,

t

:

t

,

,

u

p

y

u

p

y

u

u

p

y

R

R

⋅

α

+

⋅

α

=

⋅

α

+

⋅

α

∈

∀

∈

α

α

∀

+

20

♦

LINIOWE lub NIELINIOWE

Struktura modelu jest

liniowa wzgl

ę

dem parametrów

(LP) je

ż

eli jego

wyj

ś

cie spełnia warunek liniowo

ś

ci wzgl

ę

dem jego parametrów, t.j.

Kategorie modeli (matematycznych)

(

)

(

)

(

)

(

)

u

p

y

u

p

y

u

p

p

y

R

R

,

,

t

,

,

t

,

,

t

:

t

,

,

2

m

2

1

m

1

2

2

1

1

m

2

2

1

⋅

α

+

⋅

α

=

⋅

α

+

⋅

α

∈

∀

∈

α

α

∀

+

21

♦

Z CZASEM CI

Ą

GŁYM lub Z CZASEM DYSKRETNYM

Modele z czasem ci

ą

głym

- najcz

ęś

ciej badane ewoluuj

ą

w czasem ci

ą

głym -

st

ą

d naturalna tendencja do stosowania modeli opisywanych równaniami

ró

ż

niczkowymi

Kategorie modeli (matematycznych)

( ) (

) ( )

( )

( ) (

)

p

u

x

h

y

p

x

x

p

u

x

f

x

,

t

,

,

t

0

,

,

t

,

,

t

dt

d

m

0

=

=

=

22

♦

Z CZASEM CI

Ą

GŁYM lub Z CZASEM DYSKRETNYM

Modele z czasem dyskretnym

– zastosowanie dla systemów czasu ci

ą

głego

aproksymacji ich działania za pomoc

ą

modeli z czasem dyskretnym

Kategorie modeli (matematycznych)

( )

( ) ( )

[

]

( )

( )

( )

( ) ( )

[

]

p

u

x

h

y

p

x

x

p

u

x

f

x

,

t

,

t

,

t

t

0

,

,

t

,

t

,

t

1

t

m

0

=

=

=

+

gdzie t jest całkowitoliczbowym indeksem czasu, który odpowiada
czasowi rzeczywistemu t·T, je

ż

eli rozwa

ż

any system z czasem

ci

ą

głym jest próbkowany z okresem T

23

♦

DETERMINISTYCZNE lub NIEDETERMINISTYCZNE

W modelach systemów

deterministycznych

zmiennym i współczynnikom przypisywane

s

ą

okre

ś

lone warto

ś

ci

W modelach systemów

niedeterministycznych

co najmniej jedna zmienna lub

współczynnik ma niepewne warto

ś

ci

Kategorie modeli (matematycznych)

♦

O PARAMETRACH SKUPIONYCH lub ROZPROSZONYCH

Opis systemów ci

ą

głych o

parametrach skupionych

b

ę

dzie zawierał równania

ró

ż

niczkowe zwyczajne, natomiast o

parametrach rozproszonych

musi zawiera

ć

równania ró

ż

niczkowe cz

ą

stkowe

♦

NIESTACJONARNE LUB STACJONARNE

W modelach systemów

niestacjonarnych

co najmniej niektóre współczynniki

(parametry modelu) s

ą

funkcjami czasu, w modelach systemów

stacjonarnych

s

ą

stałe

24

Budowa modelu matematycznego

Przetworzenie całej istotnej z punktu widzenia celów modelowania
wiedzy i danych o systemie w niesprzeczny układ symboli i operatorów
matematycznych

Praktyczne wymagania jakie powinny by

ć

spełnione przy budowie modelu:

♦

zgodno

ść

z modelowanym systemem w zakresie interesuj

ą

cych

wła

ś

ciwo

ś

ci, zale

ż

no

ś

ci

♦

łatwo

ść

u

ż

ytkowania modelu zgodnie z przeznaczeniem

St

ą

d:

♣

wst

ę

pna koncepcja budowy modelu matematycznego powinna zawiera

ć

zbiór hipotez wyró

ż

niaj

ą

cych to, co jest

istotne

dla celów modelowania

i powinno znale

źć

odbicie w modelu, od tego co nale

ż

y odrzuci

ć

25

Identyfikacja modelu matematycznego

Identyfikacj

ę

modelu przeprowadza si

ę

, gdy:

wiedza teoretyczna o systemie nie wystarcza do nadania modelowi

postaci umo

ż

liwiaj

ą

cej wykonanie w oparciu o ten model oblicze

ń

;

nie

wystarcza

do

okre

ś

lenia

niektórych

lub

wszystkich

współczynników tego modelu

Identyfikacja modelu (parametrów modelu) to:

wyznaczenie ocen statystycznych (lub innych) – estymatorów

warto

ś

ci

nieznanych

parametrów

drog

ą

odpowiedniego

przetworzenia danych eksperymentalnych (pomiarowych

lub

do

ś

wiadczalnych)

26

Identyfikacja modelu matematycznego – c.d.

Wyró

ż

nia si

ę

identyfikacj

ę

:

•

biern

ą

, czynn

ą

•

jednorazow

ą

, bie

żą

c

ą

(okresow

ą

, ci

ą

gł

ą

)

Identyfikacja:

♣

bierna –

polega na gromadzeniu danych do

ś

wiadczalnych

(pomiarowych) podczas normalnej pracy systemu, a nast

ę

pnie

przetworzenie jej odpowiednimi metodami w celu wyznaczenia
estymatorów nieznanych parametrów

♣

czynna – polega na odpowiednim zaplanowaniu (plan oddziaływa

ń

wej

ś

ciowych

systemu)

i

przeprowadzeniu

eksperymentu

identyfikacyjnego, którego wyniki słu

żą

nast

ę

pnie do wyznaczenia

odpowiednimi metodami estymatorów nieznanych parametrów

27

Identyfikacja:

♣

jednorazowa – system o parametrach stacjonarnych

♣

bie

żą

ca (okresowa, ci

ą

gła) – system o parametrach

niestacjonarnych

Je

ż

eli kilka struktur rywalizuje do opisu tych samych danych, ich dobro

ć

b

ę

dzie równie

ż

porównywana z

pomoc

ą

kryterium

Parametry modelu musz

ą

by

ć

dobrane zgodnie z pewnym

kryterium

,

zwykle przez optymalizacj

ę

pewnej

funkcji kosztów

Identyfikacja modelu matematycznego – c.d.

28

Jak ustala

ć

kryterium?

Ró

ż

nica

pomi

ę

dzy wyj

ś

ciami systemu i modelu

( ) ( )

( )

p

y

y

p

e

,

t

t

,

t

m

y

−

=

jest nazywana

bł

ę

dem wyj

ś

cia

29

Jak ustala

ć

kryterium?

Najcz

ęś

ciej d

ąż

y si

ę

, aby bł

ą

d wyj

ś

cia był jak najbli

ż

szy

zeru

– to

prowadzi

do

problemu

definicji

funkcji

kryterialnej

słu

żą

cej

porównywaniu

jako

ś

ci

analizowancyh modeli.

Zwykle przyjmowana jest funkcja skalarna (funkcjonał)

j

parametrów i

ewentualnie struktury i nazywana

funkcj

ą

kosztów

Zwykle funkcja ta jest minimalizowana

Model

M(p

1

)

jest wówczas

lepszy

od modelu

M(p

2

)

w sensie kryterium

zwi

ą

zanego z funkcjonałem j, je

ż

eli

( )

(

)

( )

(

)

2

1

M

j

M

j

p

p

<

30

Weryfikacja modelu matematycznego

Weryfikacja modelu to porównanie wyników modelowania z:

♦

systemem rzeczywistym, lub

♦

z modelem wzorcowym

z punktu widzenia ich zgodno

ś

ci z wiedz

ą

teoretyczn

ą

lub z wynikami

bada

ń

do

ś

wiadczalnych

Uwaga:

Weryfikacja jest integralnie zwi

ą

zana z ka

ż

dym z poprzednich etapów

modelowania – powinna by

ć

realizowana nie tylko po zako

ń

czeniu

poprzednich etapów, lecz tak

ż

e w trakcie ich realizacji

31

Przyst

ę

puj

ą

c do weryfikacji nale

ż

y ustali

ć

kryteria, które b

ę

d

ą

stosowane dla oceny zgodno

ś

ci (ustalenia przyczyn niezgodno

ś

ci)

Wyró

ż

nia si

ę

dwie grupy kryteriów:

•

wewn

ę

trzne

•

zewn

ę

trzne

Weryfikacja modelu matematycznego

32

Kryteria wewn

ę

trzne

– dotycz

ą

tzw. wewn

ę

trznych cech modelu:

•

zgodno

ść

formalna

– brak sprzeczno

ś

ci koncepcyjnych,

logicznych i matematycznych

•

zgodno

ść

algorytmiczna

– poprawno

ść

u

ż

ytych operatorów,

algorytmów zapewniaj

ą

ca efektywne wykonywanie oblicze

ń

z

wymagan

ą

dokładno

ś

ci

ą

Weryfikacja modelu matematycznego

33

Kryteria zewn

ę

trzne

– dotycz

ą

celów modelowania i zgodno

ś

ci modelu

z wynikami bada

ń

eksperymentalnych:

•

zgodno

ść

heurystyczna

– dotyczy walorów badawczych modelu:

mo

ż

liwo

ś

ci interpretacji za jego pomoc

ą

okre

ś

lonych zjawisk

zachodz

ą

cych w systemie, sprawdzenia postawionych hipotez,

formułowania nowych zada

ń

badawczych

•

zgodno

ść

pragmatyczna

– dotyczy bezpo

ś

redniej zgodno

ś

ci

wyników z modelu systemu z danymi z systemu rzeczywistego;
stwierdzenie tej zgodno

ś

ci wymaga przede wszystkim

porównania wielko

ś

ci wyj

ś

ciowych z modelu i z systemu

rzeczywistego

Weryfikacja modelu matematycznego

34

SYSTEM

MODEL

Zakłócenia

Model

zakłóce

ń

Wielko

ś

ci

wej

ś

ciowe

Kryteria

zgodno

ś

ci

Wielko

ś

ci

wyj

ś

ciowe

Wynik

weryfikacji

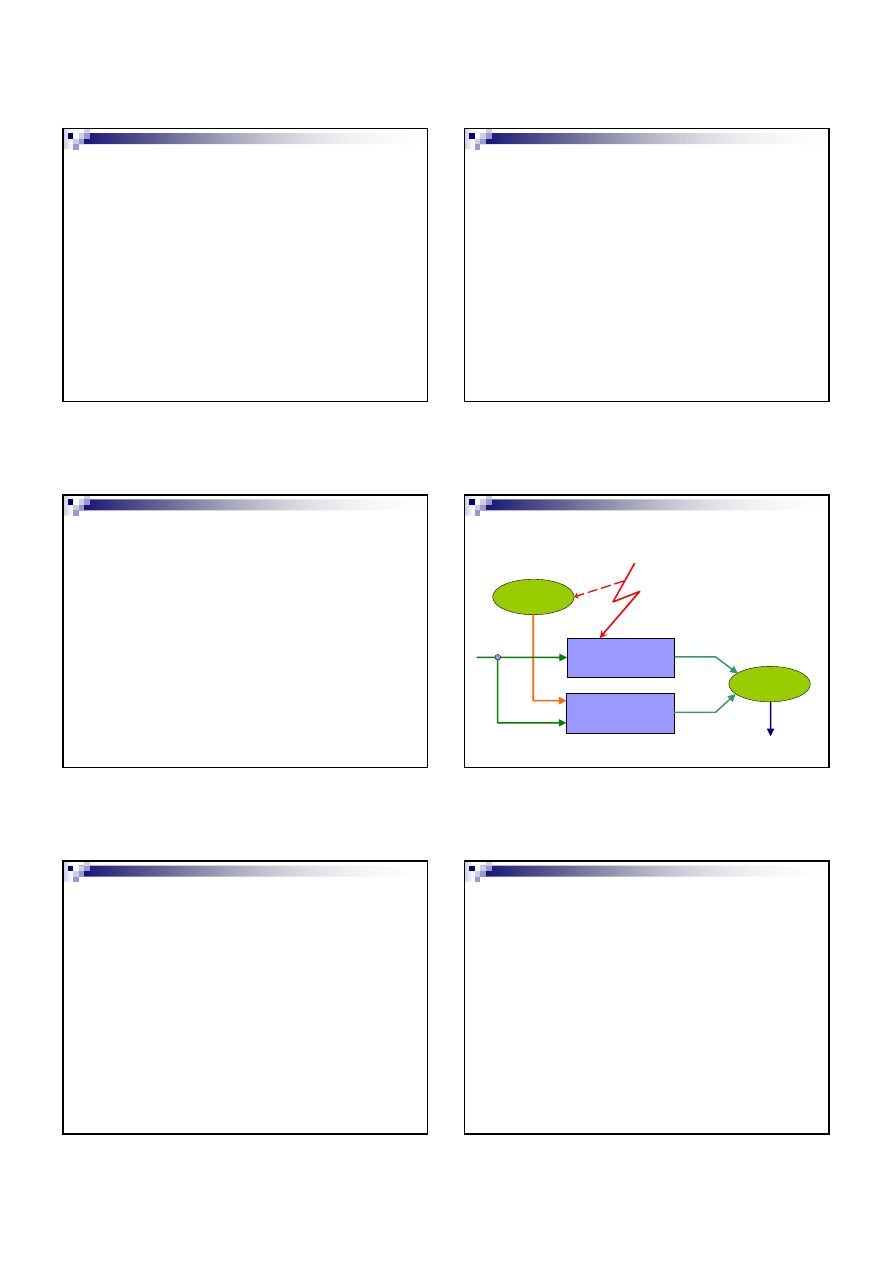
Schemat weryfikowania zgodno

ś

ci pragmatycznej

Uwaga:

•

Weryfikacja

zgodno

ś

ci

pragmatycznej

modeli

systemów nie istniej

ą

cych,

np. znajduj

ą

cych si

ę

w

stadium projektowania nie
jest w zasadzie mo

ż

liwa

35

Rodzaje zgodno

ś

ci pragmatycznej

model jest zgodny

replikatywnie

, je

ż

eli stwierdzono jego

zgodno

ść

z systemem korzystaj

ą

c podczas weryfikacji z tych

samych danych, na podstawie których dokonano identyfikacji
modelu

model jest zgodny

predykatywnie

, je

ż

eli stwierdzono jego

zgodno

ść

z systemem korzystaj

ą

c podczas weryfikacji z innych

danych, ni

ż

te na podstawie których dokonano identyfikacji

modelu; na podstawie danych zebranych w innych warunkach

model jest zgodny

strukturalnie

, je

ż

eli stwierdzono jego

zgodno

ść

z systemem nie tylko dla warto

ś

ci wielko

ś

ci

wyj

ś

ciowych, ale stwierdzono te

ż

zgodno

ść

mechanizmów

przetwarzania wielko

ś

ci wej

ś

ciowych w wyj

ś

ciowe

36

! Nie nale

ż

y nigdy oczekiwa

ć

całkowitej zgodno

ś

ci wyj

ść

modelu i

systemu rzeczywistego !

O tym czy zaobserwowane ró

ż

nice mi

ę

dzy wyj

ś

ciami modelu i

systemu pozwalaj

ą

na jego u

ż

ytkowanie, czy te

ż

nie, decyduj

ą

wyniki

testów zgodno

ś

ci

– ich konkretna tre

ść

zale

ż

y od

przeznaczenia modelu

Weryfikacja modelu matematycznego - c.d.

37

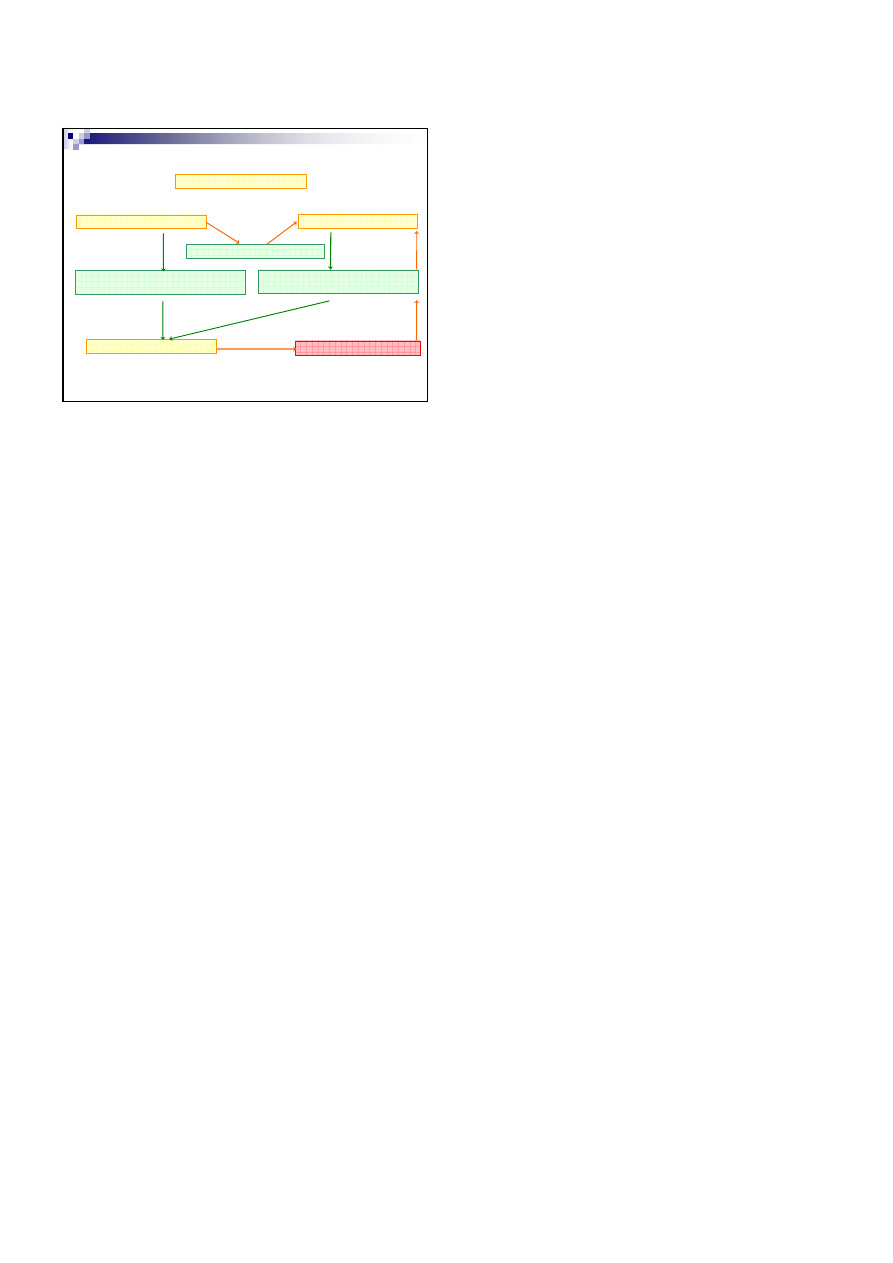
Schemat procesu modelowania matematycznego

Okre

ś

lenie celu modelowania, wybór kategorii modelu,

okre

ś

lenie struktury modelu, wybór algorytmów

System

Eksperymentator

Model matematyczny

Komputer

Wyniki

Algorytmy identyfikacji, weryfikacji,

oblicze

ń

z modelem

Dane do identyfikacji, weryfikacji, oblicze

ń

z

modelem

Dane i wiedza o systemie

Ź

ródło danych

Narz

ę

dzie przetwarzania danych w

oparciu o okre

ś

lone algorytmy

Przesłanki do

akceptacji lub zmiany

Zmiana/modyfikacja

algorytmów

Zmiana/modyfikacja

modelu