P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
1
Zad1
Oszacowano model trendu, w którym, Y oznacza wartość nakładów inwestycyjnych (w tys. zł
rocznie
Który z następujących wniosków jest prawidłowy i dlaczego?
1.
Nakłady inwestycyjne wzrastały średnio o 4,5%
2.
Nakłady inwestycyjne rocznie wzrastały średnio o 4,5%
3.
Nakłady inwestycyjne wzrastały rocznie średnio o 0,045 tys. zł rocznie
4.
Powyższe zdania są błędne. Powinno być ……….
Zad 2
Dany jest model
Gdzie t oznacza zmienną czasową. Proszę uzupełnić następujące informacje:
1.
Wzrost t o jednostkę wiąże się ze wzrostem Y o …….
2.
Jeśli w pierwszym roku Y=1000 to po roku Y = ……..
3.
Jeśli w pierwszym roku Y=5000 to po dwóch latach w przybliżeniu Y=…..
Zad 3
Niech K oznacza wielkość wydatków konsumpcyjnych w rodzinie, Y – dochody tej rodziny, N -
liczbę członków rodziny.
1.
Zaproponuj model ekonometryczny, za pomocą którego można sprawdzać następujące
hipotezy:
a.
Krańcowa skłonność do konsumpcji maleje w miarę wzrostu dochodu
b.
Krańcowy efekt liczby członków rodziny (N) na wielkość konsumpcji (K) w ,miarę
wzrostu N
2.
Zinterpretuj hipotezy z punktu 1. Czy Twoim zdaniem są słuszne?
3.
Opisz jak na podstawie danych liczbowych o zmiennych K, Y i N w grupie 1500 rodzin, jak
należało by oszacować zaproponowany model a nastę[nie za jego pomocą zweryfikować
sformułowane hipotezy.
Zad 4
Oszacowano funkcję Turnquista (II typu dla dobra podstawowego) wydatków na żywność (Y w
zł/osobę) od dochodów w grupie rodzin trzyosobowych (X w zł/osobę)
1.
Naszkicuj tę funkcję i opsz jej własności
2.
/zinterpretuj poziom nasycenia funkcji
3.
Wyznacz poziom wydatków na żywno śc , jeśli poziom dochodów wynosił 1500 zł na osobę
3
,
14
7
,
12
+
=
i
i
x
y)
P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
2
Zad 5.
Na podstawie kwartalnych danych statystycznych z lat 2006-2012 oszacowano parametry
funkcji popytu na meble i otrzymano następujące wyniki:
)
021
,
0
(
)
053
,
0
(
)
0018
,
0
(
)
13
,
0
(
)
24
,
0
(
)
41
,
0
(
)
(
395
,
0
437
,
0
312
,
0
ln
38
,
0
ln
26
,
2
ln
3
2
1
i
i
i
i
a
S
z
z
z
x
y
d
−
−
−
−
+
=
)
R
2
=0,989
DW=2,08
Gdzie:
D - popyt na meble (w mln zł)
Y - realne dochody gospodarstw domowych
X – średni popyt na meble z trzech poprzednich kwartałów (w mln zł)
Z
j
– zmienna zerojedynkowa przyjmująca wartość 1, gdy obserwacja dotyczy kwartału j oraz 0 dla
pozostałych kwartałów
t – zmienna czasowa oznaczająca numer kolejnego kwartału it=1, 2, …
1.
Zinterpretować parametry modelu.
2.
Ocenić otrzymany model pod względem merytorycznym i statystycznym.
Zad 6
Zbudować model wielorównaniowy opisujący:
−
popyt na projektory multimedialne w zależności od popytu na te produkty sprzed roku, średniej
wielkości przychodów gospodarstw domowych oraz średniej ceny biletów do kina w miastach;
−
popyt na lampy do projektorów multimedialnych jest zależny od popytu na projektory w roku
ubiegłym i bieżącym oraz od ceny projektora.
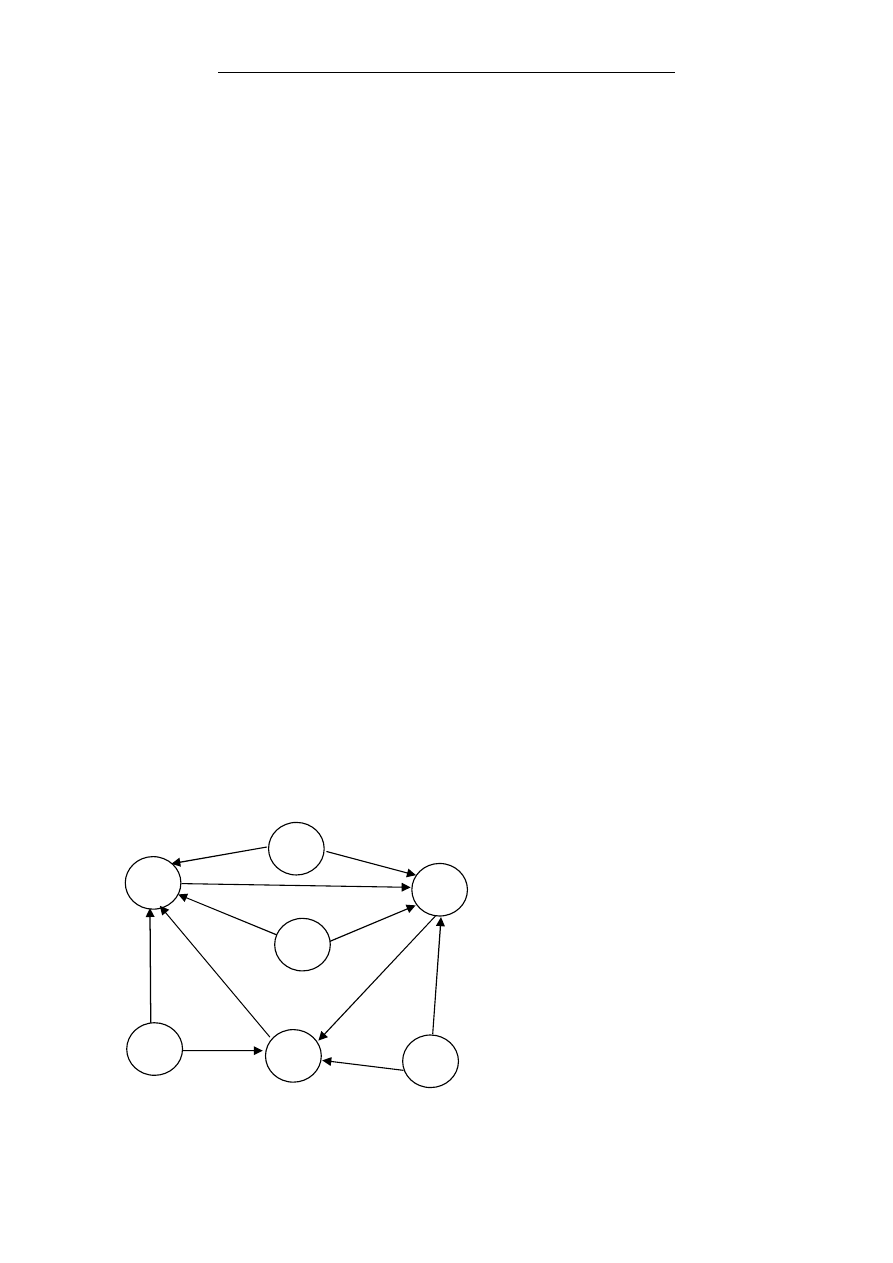
Zad 7
Dany jest graf powiązań pomiędzy odpowiednimi zmiennymi w modelu wielorównaniowym.
Zmienne endogeniczne są oznaczone symbolami Y
1
Y
2
Y
3
.
Y
1
Y
2
Y
3
X
3
X
1
X
2
X
4
1.
Określ typ tego modelu.
2.
Przyjmując w modelu zależności
liniowe zapisz postać tego modelu.
3.
Zapisz
model
w
postaci
strukturalnej. Zdefiniuj macierze
parametrów
przy
zmiennych
endogenicznych
oraz
przy
zmiennych wartościach z góry
ustalonych.
P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
3
Zad 8.
Określ typ zmiennych w poniższych modelach:
a)
t
t
t
t
t
t
t
t
t
t
t
t
t
t
k
y
p
s
p
k
u
y
u
u
y
21
3
1
32
31
2
2
23
1
22
21
1
1
1
13
1
12
11
ε
α
α
α
ε
α
α
α
α
ε
α
α
α
α
+
+
+
=
+
+
+
+
=
+
+
+
+
=
−
−
−
−
b)
t
t
t
t
t
t
t
t
t
t
t
y
x
x
s
y
x
x
x
y
2
1
4
1
1
2
1
1
1
1
4
3
3
2
2
1
1
ε
β
β
β
ε
α
α
α
α
+
+
+
=
+
+
+
+
=
−
−
−
c)
t
t
t
t
t
t
t
t
t
t
t
t
t
x
y
p
s
p
k
x
y
u
x
21
3
1
,
1
32
31
2
2
23
1
22
21
2
1
1
1
13
11
1
ε
α
α
α
ε
α
α
α
α
ε
α
α
α
+
+
+
=
+
+
+
+
=
+
+
+
=
−
−
−
Zad 9
Dokonać klasyfikacji poniższych modeli:
d)
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
u
p
u
y
s
p
k
p
y
p
u
y
21
3
1
32
1
31
2
2
24
23
1
22
21
1
1
1
13
12
11
ε
α
α
α
ε
α
α
α
α
α
ε
α
α
α
α
+
+
+
=
+
+
+
+
+
=
+
+
+
+
=
−
−
−
−
e)
t
t
t
t
t
t
t
t
t
t
t
k
x
k
s
y
x
x
x
y
2
1
3
1
1
2
1
1
1
1
4
3
3
2
2
1
1
ε
β
β
β
ε
α
α
α
α
+
+
+
=
+
+
+
+
=
−
−
−
f)
t
t
t
t
t
t
t
t
t
t
t
k
x
k
y
y
x
p
p
x
2
1
3
2
1
1
1
1
4
1
3
2
2
1
1
ε
β
β
β
ε
α
α
α
α
+
+
+
=
+
+
+
+
=
−
−
−
g)
t
t
t
t
t
t
t
t
t
t
t
t
t
y
x
x
y
y
p
x
y
u
y
21
3
1
32
1
,
1
32
1
31
3
2
2
1
23
1
22
1
21
2
1
1
11
1
ε
α
α
α
α
ε
α
α
α
α
ε
α
α
+
+
+
+
=
+
+
+
+
=
+
+
=
−
−
Zad 10
Analizując dane o miesięcznych przychodach w sprzedaży w tys. zł (Y), powierzchni sprzedaży
w m
2
(X
1
) oraz liczby zatrudnionych w osobach (X
2
) w 30 sklepach DIY oszacowano funkcję:
i
i
i
x
x
y
2
1
5
,
2
8
,
1
2
,
16
+
+
=
(
R
2
=0,96 s
e
=0,4
Przyjmując, że x
1
=1020m
2
, x
2
=45 osób, obliczyć:
- miesięczne przychody ze sprzedaży;
- produkty przeciętne;
- elastyczność przychodów ze sprzedaży;
- krańcowe stopy substytucji.
P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
4
Zad 11
W pewnym przedsiębiorstwie produkującym akcesoria wędkarskie oszacowano dynamiczną
funkcję produkcji:
t
i
e
x
x
y
13
,
0
8
,
0
2
6
,
0
1
6
,
15
=
Podać interpretację elastyczności produkcji względem badanych czynników produkcji
Określić efekt skali produkcji.
Zad 12
Zbadać identyfikowalność następujących modeli
a)
t
t
t
t
t
t
t
t
t
t
t
y
x
x
s
y
x
s
x
y
2
0
4
1
1
2
1
1
1
0
1
4
3
3
2
1
1
ε
β
β
β
β
ε
α
α
α
α
α
+
+
+
+
=
+
+
+
+
+
=
−
−
b)
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
p
u
u
y
u
p
k
p
y
p
u
y
21
3
32
1
31
2
2
24
23
1
22
21
1
1
1
13
12
11
ε
α
α
α
ε
α
α
α
α
α
ε
α
α
α
α
+
+
+
=
+
+
+
+
+
=
+
+
+
+
=
−
−
−
Zad 13
Dla modeli postaci:
a)
04
,
18
11
,
3
14
,
0
99
,
2
22
,
14
18
,
2
11
,
9
21
,
2
13
,
0
3
1
1
1
1
3
2
1
−
+
+
−
=
+
+
−
+
=
−
−
t
t
t
t
t
t
t
t
t
k
x
k
s
y
x
x
x
y
b)
17
,
8
31
,
3
84
,
2
89
,
0
65
,
2
14
,
2
46
,
0
25
,
1
21
,
2
13
,
3
18
,
0
44
,
2
1
1
1
+
+
+
=
+
+
+
−
=
−
+
=
−
−
−
t
t
t
t
t
t
t
t
t
t
t
t
p
u
p
u
y
s
p
k
p
p
u
y
c)
61
,
9
11
,
8
11
,
6
65
,
2
41
,
7
25
,
2
18
,
3
78
,
4
16
,
5
13
,
3
14
,
5
13
,
3
17
,
8
3
1
1
,
1
2
3
2
3
1
1
2
1
2
1
+
−
+
+
=
+
+
−
−
=
+
+
=
−
−
t
t
t
t
t
t
t
t
t
t
t
t
t
x
y
x
y
y
x
y
p
y
y
x
y
y
d)
21
,
77
65
,
12
21
,
2
81
,
3
02
,
87
64
,
5
12
,
87
06
,
13
21
,
2
1
1
1
2
1
1
,
1
2
1
1
+
−
+
−
=
+
+
−
+
=
−
−
−
t
t
t
t
t
t
t
t
t
k
x
k
x
y
x
x
p
x
e)
3
,
18
08
,
23
65
,
11
01
,
19
88
,
14
99
,
102
94
,
22
38
,
17
08
,
13
05
,
22
1
,
2
1
1
1
2
1
3
2
2
1
+
+
+
+
=
+
+
−
+
=
−
−
−
t
t
t
t
t
t
t
t
t
t
s
k
s
k
s
y
x
x
s
s
Proszę wyznaczyć (o ile to możliwe) postać zredukowaną modelu.
Zad 14
Dyrekcja jednego ze szpitali, dążąc do ograniczenia masowej emigracji zarobkowej lekarzy
postanowiła znaleźć wszystkie przyczyny exodusu lekarzy. Na podstawie badań stwierdzono, że
największy wpływ na emigrację zarobkową ma:
średnia miesięczna liczba całodobowych dyżurów oraz średnia kwartalna premia.
P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
5
Premia (obliczana
jako procent
podstawy pensji)
Średnia liczba
dyżurów
całodobowych
Liczba lekarzy
w roku
poprzednim
Liczba lekarzy,
którzy wyjechali za
granicę
15-20
5
10
6
15-20
8
15
6
20-25
6
10
4
20-25
4
5
1
20-25
1
4
1
(
)
−
−
−
−
−
−
−
−
=
−
−
−
0,14
0,01
0,16
0,08
0,08
0,01
0,03
0,18
0,07
0,13
1,2
0,5
4,2
1,17
3,33
L
T
L
T
1
1
1
Ω
X
X
Ω
X
a)
Na podstawie informacji z powyższej tabeli zbudować model logitowy, opisujący
prawdopodobieństwo wyjazdu lekarza w ciągu roku;
b)
Jakie jest prawdopodobieństwo zwolnienia się lekarza z kwartalną premią 18%, który
miesięcznie pełni 5 dyżurów całodobowych?
c)
Jaką postać ma w badanym modelu macierz
1
−
L
Ω
.
d)
Proszę wyznaczyć prawdopodobieństwa teoretyczne dla każdej z badanych grup.
e)
Jaka jest interpretacja parametrów stojących przy zmiennych w modelu logitowym?
Zad 15 Oszacowano liniową funkcję popytu na czereśnie:
Z
C
C
Y
13
,
2
48
,
2
21
,
4
28
,
3
2
1
+
+
−
=
)
gdzie: Y - popyt na czereśnie (w kg); C
1
– cena za 1 kg czereśni (w zł); C
2
– cena za 1 kg truskawek
Z – dochód konsumenta.
Przeprowadzić ekonometryczną analizę popytu wyznaczając elastyczność punktową mając dane:
C
1
=6,27, C
2
=4,50 D=4210 zł.
Zad 16 Na podstawie danych statystycznych z 1989-2010 szacowano parametry pewnej funkcji
samochodów Y (w tys sztuk) w zależności od majątku produkcyjnego K w roku t (w mln zł),
zatrudnienia pracowników L w roku t. Otrzymano następujące wyniki:
_
)
011
,
0
(
)
041
,
0
(
)
082
,
0
(
)
291
,
0
(
)
(
034
,
0
ln
386
,
0
ln
753
,
0
167
,
3
ln
i
t
t
t
a
S
t
l
k
y
+
+
+
=
)
R
2
=0,94
1.
Zapisz wyjściową postać modelu.
P
RZYKŁADOWE ZADANIA NA KOLOKWIUM Z PRZEDMIOTU
E
KONOMETRIA
II
6
2.
Zinterpretuj otrzymane parametry i oceń czy model jest poprawny merytorycznie.
3.
Które zmienne w modelu są statystycznie istotne?
Zad 17 Dana jest postać strukturalna modelu wielorównaniowego:
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
z
s
p
x
y
x
z
z
y
p
y
x
2
20
24
23
1
22
21
21
30
1
32
1
31
1
10
1
13
12
11
ε
β
β
β
β
β
ε
β
β
β
ε
β
β
β
β
+
+
+
+
+
=
+
+
+
=
+
+
+
+
=
−
−
−
−
1.
Określ typ zmiennych w modelu
2.
Zbudować postać strukturalną w formie macierzowej
3.
Określ typ modelu
Zad 18 Dla danych przedstawiających koszty produkcji obuwia sportowego w przedsiębiorstwie
JUNIOR zbudowano trzy modele (zawierające różne zestawy zmiennych objaśniających). Na
podstawie poniższych informacji oceń, który model jest najlepszy i prawidłowo zbudowany.
Uzasadnij wybór modelu
Statystyki
Bł
ą
d
standar
dowy
reszt
R-
kwadra
t
AIC
Statystyka F
Statystka
empiryczna
dla Testu RESET
Model 1
(wykładnicza)
80666,6 0,7424
5
740,42 37,4752
(warto
ść
p <
0,00001)
F = 5,9618
(warto
ść
p <
0,0001)
Model 2
(liniowy)
49208,7 0,8348
8
2325,2
8
232,588
(warto
ść
p <
0,00001)
F = 2,11
(warto
ść
p
=0,12171)
Model 3
(wielomian
stopnia drugiego)
27770,1 0,5565 1540,8
2
39,5252
(warto
ść
p < 0,00001)
F = 0,298
(warto
ść
p =0,742)