Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 1

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

Informacja do zadania 1.
Dzwon Zygmunt jest częścią zespołu historycznych dzwonów zawieszonych na wieży Zygmuntow-
skiej katedry wawelskiej. Wykonał go ludwisarz Hans Beham z Norymbergi w 1520 roku. Dzwon
został wykonany z brązu, który zawiera 80% miedzi i 20% cyny, i waży 12600 kg (w tym serce
dzwonu – 365 kg). Na wieży umieszczono go 9 lipca 1521 roku, natomiast 13 lipca 1521 roku
Kraków po raz pierwszy usłyszał jego głos.

1.

Uzupełnij zdania.

a) Do wykonania dzwonu Zygmunt użyto

. . . . . . . . . . . . . .

kg cyny.

b) Serce dzwonu Zygmunt zawiera

. . . . . . . . . . . . . .

kg miedzi.

c) Dzwon Zygmunt wykonano w

. . . . . . . . . . . . . .

roku. (Zapisz datę za pomocą cyfr rzymskich).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.

W lokalnej gazecie podano informację, że w Gimnazjadzie Młodzieży Szkolnej uczestniczyło

1750 uczniów. Liczba ta stanowi pewne zaokrąglenie rzeczywistej liczby zawodników.

a) Podkreśl wszystkie poprawne przybliżenia.

I. 1744 ≈ 1750

II. 1746 ≈ 1750

III. 1755 ≈ 1750

IV. 1745 ≈ 1750

b) Jaka może być maksymalna różnica między największą a najmniejszą możliwą liczbą zawod-
ników? Zapisz obliczenia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.

Oblicz wartość wyrażenia: (0

,25)

−2

+ 0

,3

2

. Otrzymana liczba jest:

A. większa od 16.

TAK

NIE

B. ujemna.

TAK

NIE

C. równa

3

1
3

−1

+ 15

,79.

TAK

NIE

D. liczbą przeciwną do liczby (−16

,09).

TAK

NIE

4.

Liczbę

√

125 można zapisać jako:

A. 25

√

5

B. 5

√

5

C. 5

√

25

D. 25

√

25

5.

Dany jest ciąg liczb: 3, 8, 13, 18, 23, . . .. Kolejne liczby w tym ciągu są tworzone według pewnej

zasady. Odkryj ją i uzupełnij zdania.

a) Dziewiąta liczba w tym ciągu to

. . . . . . . . . . . .

.

b)

N-ta liczba w tym ciągu to

. . . . . . . . . . . . . . . . . . . . . . . .

.

6.

Które spośród liczb 0

,(3);

1

,21; (−5)

−1

są najbardziej oddalone od siebie na osi liczbowej?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

7.

Nad Sopotem, miastem o powierzchni 17 km

2

, przeszła gwałtowna ulewa, w wyniku której

spadło 80 mm deszczu. Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

W czasie ulewy na miasto spadło 136

· 10

6

litrów wody.

prawda

fałsz

W czasie ulewy na miasto spadło 1

,36 · 10

9

litrów wody.

prawda

fałsz

W czasie ulewy na miasto spadło 1

,36 · 10

5

litrów wody.

prawda

fałsz

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Informacja do zadań 9, 10.

Aby obliczyć masę idealną dla kobiety (wg P. Broca), należy od wzrostu [w cm] odjąć 100, a na-
stępnie obliczyć 85% tej wartości – otrzymamy wówczas idealną masę [w kg].

8.

Jaka jest idealna masa dla kobiety o wzroście 170 cm?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9.

Niech

x oznacza wzrost kobiety w centymetrach. Którym wyrażeniem nie można wyrazić opi-

sanej wyżej reguły obliczania idealnej masy dla kobiet?

A. 0,85(x − 100)

B. x − 100 − 0,15(x − 100)

C. 0,85x − 85

D. 0,85x − 100

10.

Z poniższego diagramu można odczytać natężenie dźwięku (w decybelach) kilku źródeł

dźwięku. Na tej podstawie odpowiedz na pytania.

a) Dźwięk powyżej 100 dB uszkadza słuch. Które źródła dźwięku uszkadzają słuch?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b) Jakie natężenie dźwięku jest uznawane za próg bólu, jeśli wiemy, że jest ono o 40 dB większe
niż praca młota pneumatycznego?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c) O ile głośniejszy jest koncert muzyki techno od dźwięków okolic podmiejskich?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Udowodnij, że dla dowolnego

x = 0 iloczyn wyrażenia x

−3

· x

8

:

x

2

x

(

x

2

)

3

przez

x jest równy x

−3

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

[mplus-gray]

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 2

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

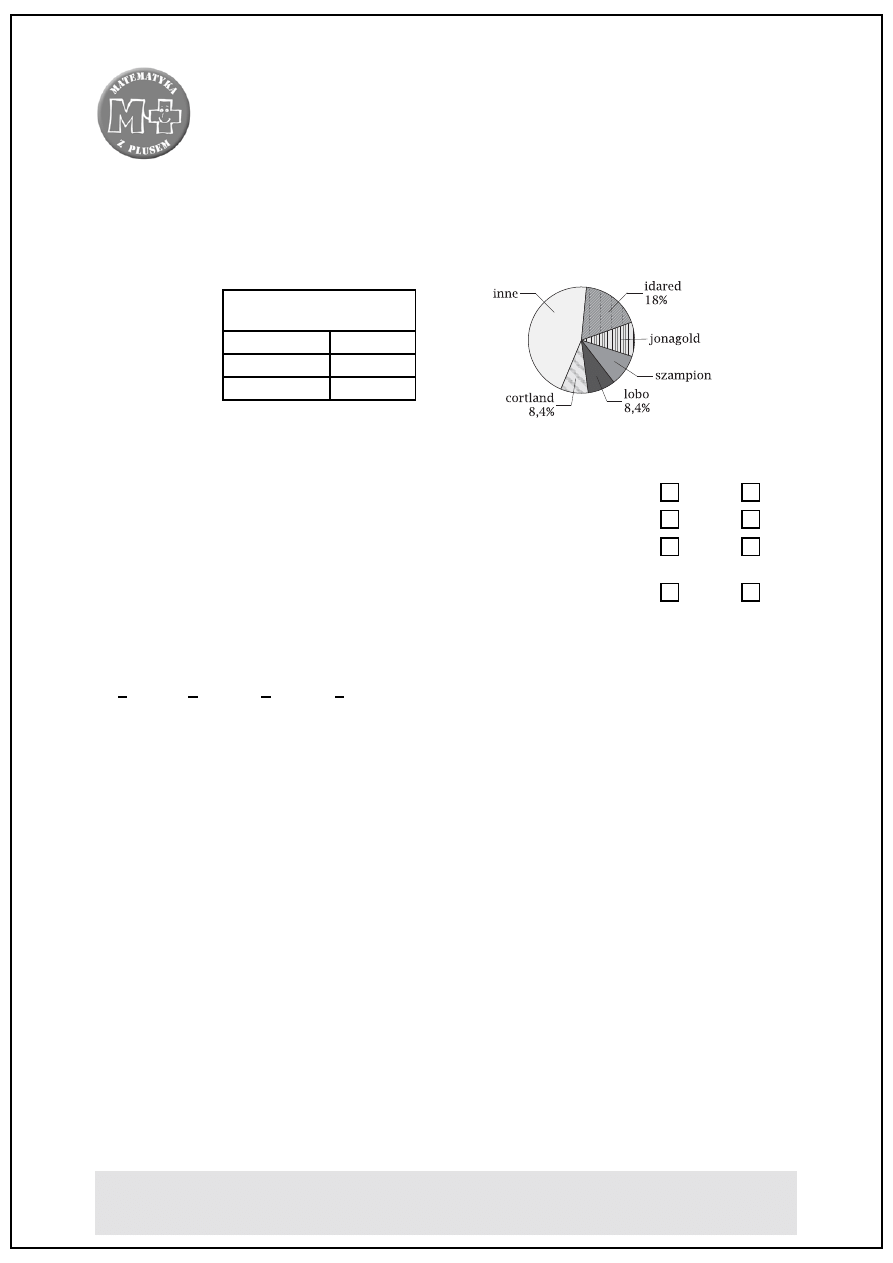
1.

Diagram przedstawia udział procentowy poszczególnych odmian jabłek w całkowitych zbio-

rach jabłek w Polsce.

[3powt3-5]

Zbiory niektórych odmian
jabłek w Polsce (w tonach)

idared

450 tys.

jonagold

260 tys.

szampion

240 tys.

Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

W Polsce zebrano 2 500 000 ton jabłek.

TAK

NIE

Jonagoldy stanowią 9% wszystkich zebranych jabłek.

TAK

NIE

20% masy wszystkich zebranych jabłek stanowiły łącznie jabłka
odmian jonagold i szampion.

TAK

NIE

W Polsce zebrano 210 000 ton jabłek lobo.

TAK

NIE

2.

W koszu znajdowało się 9 jabłek odmiany idared, 6 jabłek jonagold, 5 jabłek lobo. Janek wybrał

jedno jabłko. Prawdopodobieństwo wylosowania przez niego jabłka lobo wynosi:

A.

5
9

B.

5
6

C.

1
4

D.

1
5

3.

Jola za dwa zeszyty i długopis zapłaciła 21 zł. Antek za taki sam zeszyt i dwa długopisy zapłacił

o 5,50 zł mniej. Który z układów równań opisuje daną sytuację? (z – oznacza cenę zeszytu, d –
cenę długopisu).

A.

z + 2d = 21
2z + d = 15,50

B.

2z + d = 21
z + 2d = 15,50

C.

2z + d = 21
z + 2d = −5,50

D.

z + 2d = 21
2z + d = 5,50

4.

Ania ma a lat, a jej siostra Basia jest od niej o 7 lat młodsza. Które wyrażenia opisują, ile lat

łącznie będą miały siostry za 5 lat? Wskaż wszystkie poprawne odpowiedzi.

I. a + a + 10

II. a + 5 + a − 7 + 5

III. a + a − 7 + 5

IV. 2a + 3

V. 2a − 2

Informacja do zadań 5. oraz 6.
W pewnym szkolnym zespole szachistów wszyscy uczniowie dostają kieszonkowe. Ośmiu uczniów
dostaje kieszonkowe w kwocie 150 zł, pięciu – 100 zł, a trzech – 80 zł.

5.

Mediana kwoty kieszonkowego w tym zespole jest równa:

A. 150 zł

B. 80 zł

C. 125 zł

D. 100 zł

6.

Średnia kwota kieszonkowego w zespole szachistów jest równa

. . . . . . . . . . . . . .

zł.

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

7.

Dany jest prostokąt o prostopadłych bokach długości 2x + 2 i 3x + 1. Oceń prawdziwość zdań.

Wstaw znak

X

w odpowiednią kratkę.

Dla x = 1 dany prostokąt jest kwadratem.

TAK

NIE

Dla x = 2 obwód tego prostokąta wynosi 40.

TAK

NIE

Pole tego prostokąta wyraża się wzorem P = 6x

2

+ 2.

TAK

NIE

Obwód tego prostokąta jest równy 10x + 6.

TAK

NIE

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.

Liczba przekątnych w wielokącie o n bokach wyraża się wzorem: p = n

(n − 3)

2

. Uzupełnij zdania.

Ośmiokąt ma

. . . . . . . . . . . .

przekątnych.

Wielokąt o

. . . . . . . . . . . .

bokach ma 35 przekątnych.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

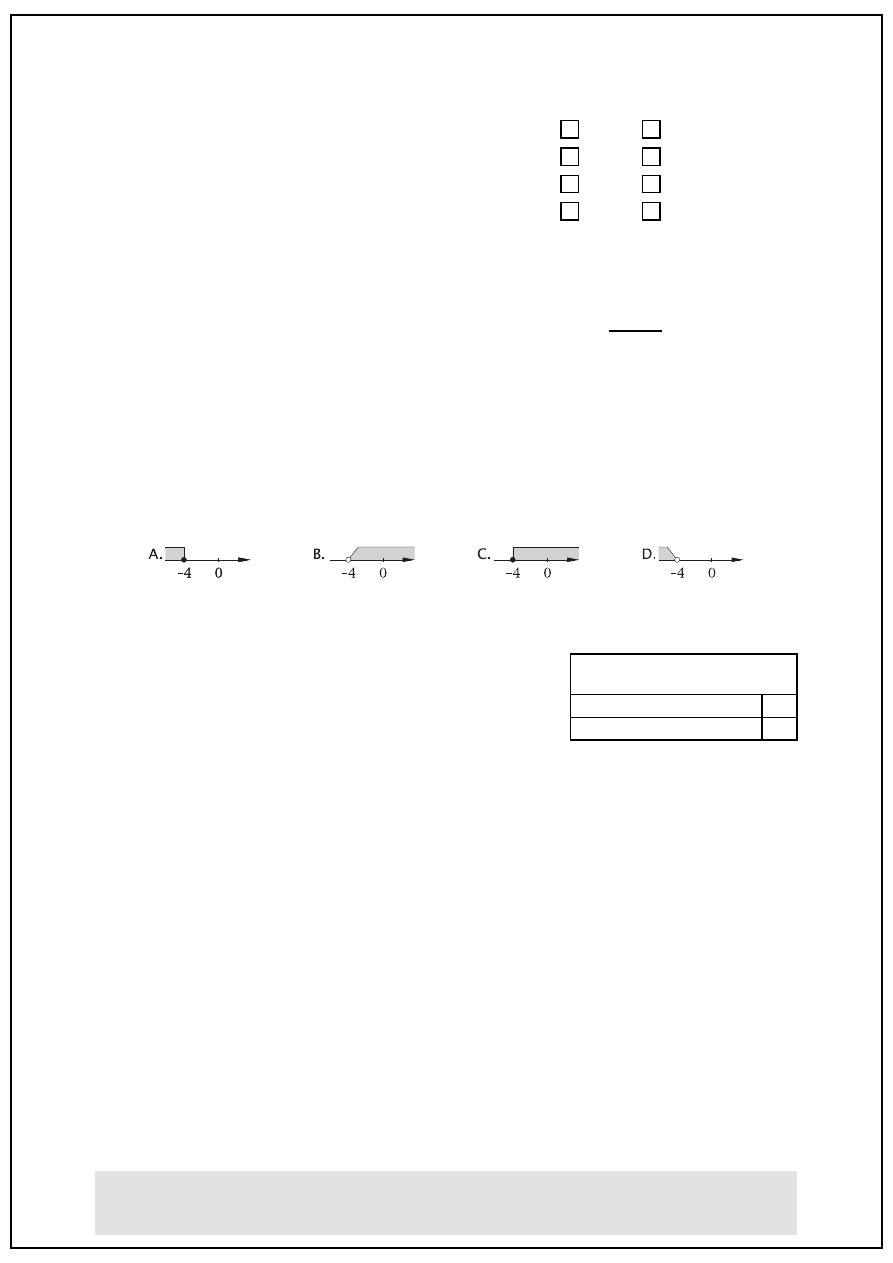
9.

Dopasuj rysunek do każdej z podanych nierówności.

I. x ≥ −4

II. x < −4

[3powt3-6]

I –

. . . . . . .

oraz II –

. . . . . . .

10.

Ceny biletów do Muzeum

Regionalnego

dzieci i młodzież szkolna

5 zł

dorośli

8 zł

Biuro turystyczne „Skalnik” oferuje jednodniową wyciecz-

kę szkolną w cenie 40 zł za osobę (oferta nie uwzględnia cen
biletów do muzeum, teatru itp.). Dodatkową propozycją w pro-
gramie wycieczki jest zwiedzanie Muzeum Regionalnego. Grupa
dzieci wraz z opiekunami przyjęła propozycję biura turystycz-
nego „Skalnik”. Za wycieczkę (bez opłat dodatkowych) zapłacono w sumie 1320 zł. Bilety do Mu-
zeum Regionalnego kosztowały łącznie 174 zł. Ile dzieci i ilu dorosłych wzięło udział w wycieczce?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Udowodnij, że różnica liczby dwucyfrowej i liczby o tych samych cyfrach (od większej liczby

odejmujemy mniejszą), lecz zapisanych w odwrotnej kolejności jest podzielna przez 9.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM
Zestaw zadań nr 3

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

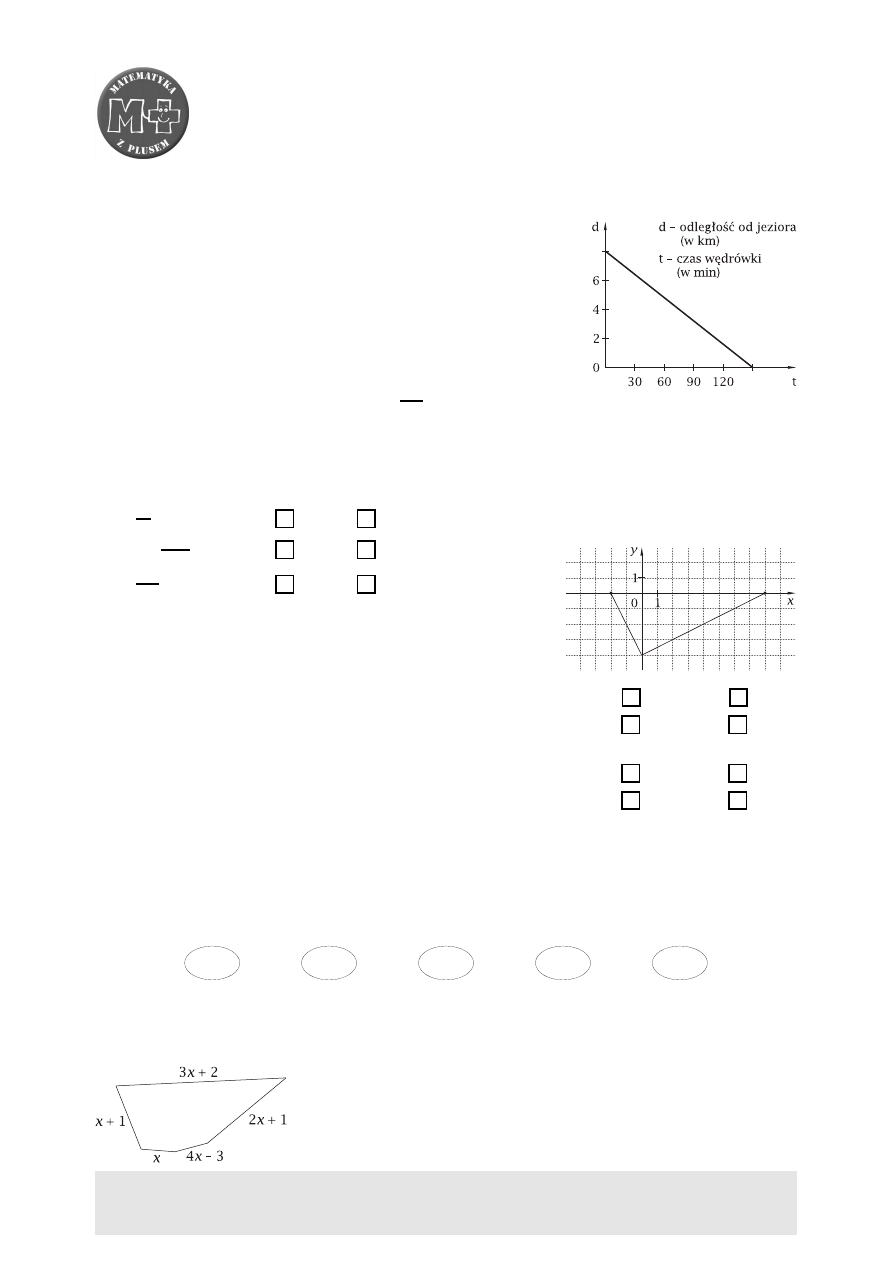
1.

Gimnazjaliści z koła ekologicznego postanowili rozbić obóz

nad leśnym jeziorem. Wyruszyli tam razem z leśniczym wcze-
śnie rano. Na wykresie obok przedstawiono zależność między
odległością wędrowców od jeziora a czasem wędrówki. Odczy-
taj informacje z wykresu i uzupełnij zdania:

Gimnazjaliści podczas wyprawy nad leśne jezioro przeszli

. . . . . . . . . . . . . .

km. Wyprawa trwała

. . . . . . . . . . . . . .

godz. Średnia prędkość

wędrujących ekologów wyniosła

. . . . . . . . . . . . . .

km

h

.

2.

Dźwięk w wodzie pokonuje w ciągu sekundy drogę równą 1,4 · 10

5

cm. Prędkość dźwięku

w wodzie wynosi:

1400

m

s

TAK

NIE

8,4 · 10

5

cm

min

TAK

NIE

5040

km

h

TAK

NIE

3.

Korzystając z przedstawionego obok wykresu, oceń praw-

dziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Funkcja przyjmuje wartość −2 dokładnie dla dwóch argumentów.

prawda

fałsz

Dla argumentów większych od 0 funkcja przyjmuje wartości
dodatnie.

prawda

fałsz

Dla argumentu 4 funkcja przyjmuje wartość 0.

prawda

fałsz

Dla argumentu 1 funkcja przyjmuje wartość dodatnią.

prawda

fałsz

4.

Wybierz spośród poniższych liczb wszystkie te, które spełniają jednocześnie trzy warunki:

• Liczba ta jest podzielna przez 4.

• Pierwiastek sześcienny z tej liczby jest liczbą całkowitą.

• Liczba ta jest wielokrotnością liczby 5.

100

64

8000

25

1000

5.

Na rysunku przedstawiono pięciokąt oraz oznaczono związki między długościami jego boków.

Uzupełnij zdania, wpisując odpowiednie wyrażenia algebraiczne.

a) Obwód pięciokąta, zapisany w najprostszej postaci, wynosi

. . . . . . . . . . . . . . . . . . .

.

b) Bok sześciokąta foremnego o obwodzie równym obwodowi

narysowanego pięciokąta ma długość

. . . . . . . . . . . . . . . . . . .

.

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

6.

Wiadomo, że

2

5

·3

7

6

4

= 54. Ile jest równe

2

6

·3

8

6

5

?

A.

27

B.

54

C.

108

D.

162

7.

Która z poniższych liczb leży na osi liczbowej najbliżej liczby 5?

A.

15

1
3

+

−10

2
9

B.

−7

6
7

+ 12

5
6

C.

−6

2

· (−

1
7

)

D.

1

2
5

:

2
7

8.

Rozwiązaniem układu równań

3y − 2x + 1 = 10
y

= 2x − 1

jest:

A.

para liczb dodatnich.

B.

para liczb ujemnych.

C.

para liczb o przeciwnych znakach.

D.

nieskończenie wiele par (x, y), które spełniają równanie y = 2x − 1.

9.

Oblicz pole działki w kształcie prostokąta o wymiarach 250 m × 1,6 km. Wynik podaj w m

2

i przedstaw w notacji wykładniczej.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

10.

Ołówek kosztuje 50 groszy. Jeśli kupujemy więcej niż 10 ołówków, to za każdy następny

płacimy o 20% mniej. Ile ołówków można kupić za 7 zł?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Uzasadnij, że różnica pól trójkątów powstałych w wyniku rozcięcia trapezu wzdłuż jednej

jego przekątnej jest równa różnicy pól trójkątów powstałych w wyniku rozcięcia tego trapezu
wzdłuż drugiej przekątnej. (Uwaga. Od większego pola odejmij mniejsze.)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

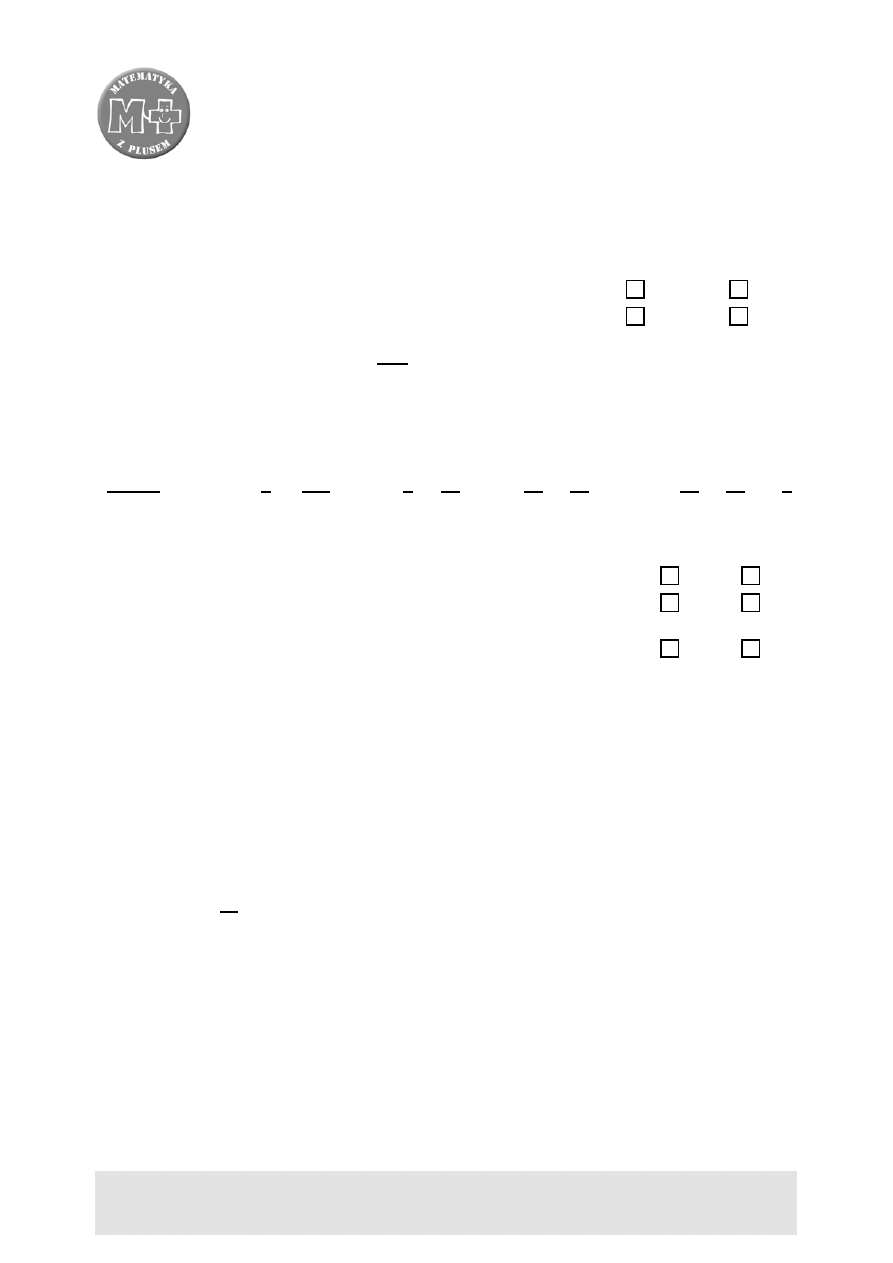
Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 4

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

1.

Miary kątów trójkąta ostrokątnego wynoszą odpowiednio

α, α + 20◦, 2α. Oceń prawdziwość

zdań. Wstaw znak

X

w odpowiednią kratkę.

Miara jednego kąta jest dwa razy mniejsza od miary drugiego
kąta i o 20◦ mniejsza od miary trzeciego kąta.

prawda

fałsz

Miary kątów w tym trójkącie wynoszą 32◦, 64◦, 86◦.

prawda

fałsz

2.

Funkcja jest określona wzorem

y = x

− 3
2

. Uzupełnij zdania, wpisując odpowiednie liczby.

Wartość funkcji dla argumentu 1 wynosi

. . . . . . . . . . . . . .

. Funkcja przyjmuje wartość 0 dla argumentu

. . . . . . . . . . . . . .

. Do wykresu tej funkcji należy punkt

A = (−9,

. . . .

).

3.

Podkreśl równości fałszywe.

√

16 + 25 = 9

5

3

√

2 =

3

√

250

2

√

7 =

√

14

√

16 +

√

25 = 9

√

75 +

√

12 = 7

√

3

4.

Oceń, czy podane zdania są prawdziwe. Wstaw znak

X

w odpowiednią kratkę.

Średnia arytmetyczna zestawu ocen 1, 2, 6, 3 wynosi 3.

TAK

NIE

Średnia arytmetyczna zestawu ocen 3, 2, 6, 5, 3, 4, 5 jest równa
jego medianie.

TAK

NIE

Po dopisaniu 5 do zestawu ocen 1, 6, 3, 2 mediana zwiększy się o 1.

TAK

NIE

5.

Połącz figurę z informacją na temat liczby jej środków i osi symetrii.

N
X

I. Figura ma środek symetrii więcej niż jedną oś symetrii.
II. Figura nie ma osi symetrii i ma jeden środek symetrii.
III. Figura ma jedną oś symetrii i nie ma środka symetrii.
IV. Figura nie ma osi symetrii i nie ma środka symetrii.

6.

Podstawa fontanny ma kształt połowy koła. Pole powierzchni tej podstawy jest równe 6,93 m

2

.

Czy zaprojektowana w ten sposób fontanna zmieści się na wyznaczonej w parku powierzchni
w kształcie prostokąta o wymiarach 2

,5 m × 4 m?

Przyjmij, że

π ≈

22

7

. Zapisz wszystkie obliczenia i uzasadnij odpowiedź.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

7.

Które z przedstawionych trójkątów są równoramienne? Zapisz obliczenia i uzasadnij swoją

odpowiedź.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.

W miejsce kratek wstaw odpowiednie cyfry, tak aby utworzona w ten sposób liczba pięciocy-

frowa była podzielna przez 15. Wypisz wszystkie możliwe przypadki.

576

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9.

W poniższej tabeli przedstawiono zawartość soli w wybranych wodach morskich.

Morze Bałtyckie

7 ‰

Morze Czarne

2 %

Morze Czerwone

4,2 %

a) Ile soli jest w 35 kg wody z Bałtyku, a ile w tej samej ilości
wody z Morza Czarnego?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b) Czy w 45 kg wody z Morza Czerwonego jest mniej czy więcej niż 2 kg soli? O ile?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

10.

Punkty

A i B są symetryczne względem osi y, a punkty A i C są

symetryczne względem osi

x. Oblicz współrzędne punktów A, B i C.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

A =

. . . . . . . . . . . .

,

B =

. . . . . . . . . . . .

,

C =

. . . . . . . . . . . .

.

11.

Średnia arytmetyczna liczb

a oraz b jest równa x. Wykaż, że średnia arytmetyczna liczb a, b

oraz

x jest także równa x.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM
Zestaw zadań nr 5

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

1.

Liczby ze zbioru {0,07

−2

; 1,5 · 10

2

; XCIV; 10

3

√

−64; XLIX} dopasuj do liter na osi liczbowej.

A =

. . . . . . . . . . . . . .

B =

. . . . . . . . . . . . . .

C =

. . . . . . . . . . . . . .

D =

. . . . . . . . . . . . . .

E =

. . . . . . . . . . . . . .

2.

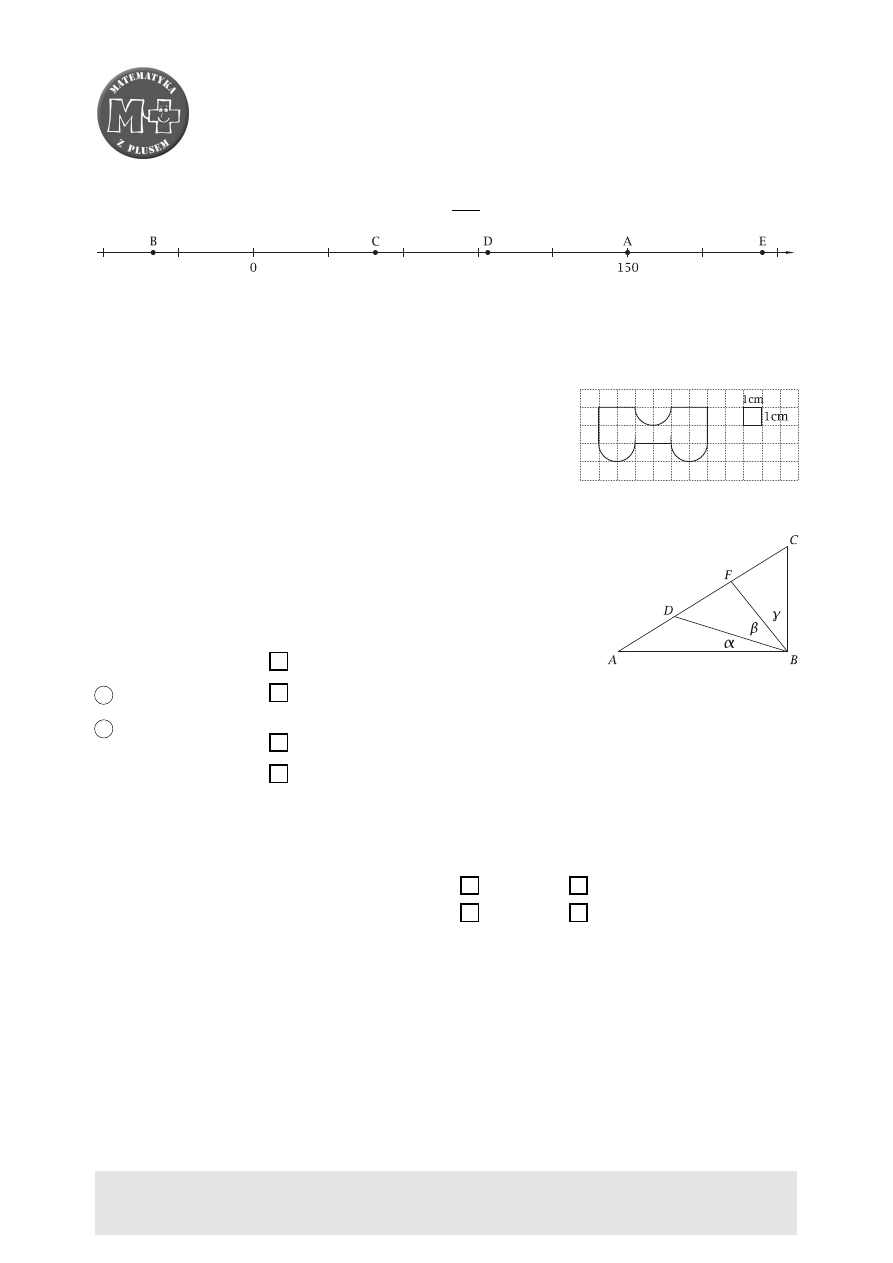
Jacek narysował w kratkach uproszczony rysunek wagonika. Kwadrat siatki ma bok długości

1 cm. Uzupełnij zdania.

a) Obwód wagonika jest równy

. . . . . . . . . . . . . . . . . . .

cm.

b) Pole wagonika wynosi

. . . . . . . . . . . . . . . . . . .

cm

2

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.

Punkty D i F dzielące przeciwprostokątną trójkąta ABC na

trzy równe części połączono z wierzchołkiem kąta prostego. Czy
otrzymane w ten sposób trzy trójkąty mają równe pola? Wybierz
poprawną odpowiedź i jedno jej uzasadnienie.

TAK,

NIE,

ponieważ

kąty α, β, γ są równe.

otrzymane trójkąty mają takie same wysokości i podstawy tej sa-
mej długości.

odcinki DB i FB są różnej długości.

trójkąt ABC nie jest równoramienny.

4.

Żakiet kosztuje x zł. Spódnica jest o 20% tańsza od żakietu. Komplet (żakiet i spódnica) kosz-

tuje 270 zł. Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Spódnica kosztuje 150 zł.

prawda

fałsz

Żakiet jest o 20% droższy od spódnicy.

prawda

fałsz

5.

Jacek miał dwa naczynia w kształcie sześcianu; jedno o krawędzi 3 dm, a drugie o krawędzi

5 dm. Do mniejszego sześcianu nalał wody do pełna, a następnie przelał ją do większego sze-
ścianu. Uzupełnij zdania. Zapisz obliczenia.

a) Objętość małego sześcianu wynosi

. . . . . . . . . . . . . .

litrów.

b) Woda w dużym sześcianie będzie sięgać na wysokość

. . . . . . . . . . . . . .

cm.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

6.

Spośród podanych niżej liczb wybierz wszystkie liczby równe 0,3

4

.

A. p0,09 · 10

4

B. 2

4

:

6 2

3

4

C. 9

2

· 10

−5

D. 3

3

· 3 · 10

−4

E. 81 : 10

4

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.

Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Połowa liczby 2

52

to 2

26

.

prawda

fałsz

Trzecia część liczby 3

12

to 3

11

.

prawda

fałsz

Pięciokrotność liczby 5

35

to 5

36

.

prawda

fałsz

Druga potęga liczby 7

17

to 7

19

.

prawda

fałsz

8.

Wskaż wszystkie równania, których nie spełnia żadna liczba.

A. 5x − 10 = −5(2 − x)

B. 5(x − 1) = 5x − 1

C. x + 5 = −5

D. 5x = 0

E. x

2

+ 5 = 0

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9.

Pod każdym układem równań podano parę liczb, która jest rozwiązaniem tego układu. Wpisz

w każdą lukę odpowiednią liczbę.

A.

x + y =

. . . . . . . . . . . . . .

x − y =

. . . . . . . . . . . . . .

Rozwiązaniem układu jest
para liczb (4, −1).

B.

3x − y =

. . . . . . . . . . . . . .

2x + 5y =

. . . . . . . . . . . . . .

Rozwiązaniem układu jest
para liczb (−2, 0).

C.

x + 6y − 8, 5 =

. . . . . . . . . . . . . .

−x − 3y + 4 =

. . . . . . . . . . . . . .

Rozwiązaniem układu jest
para liczb (−1,5, 2,5).

10.

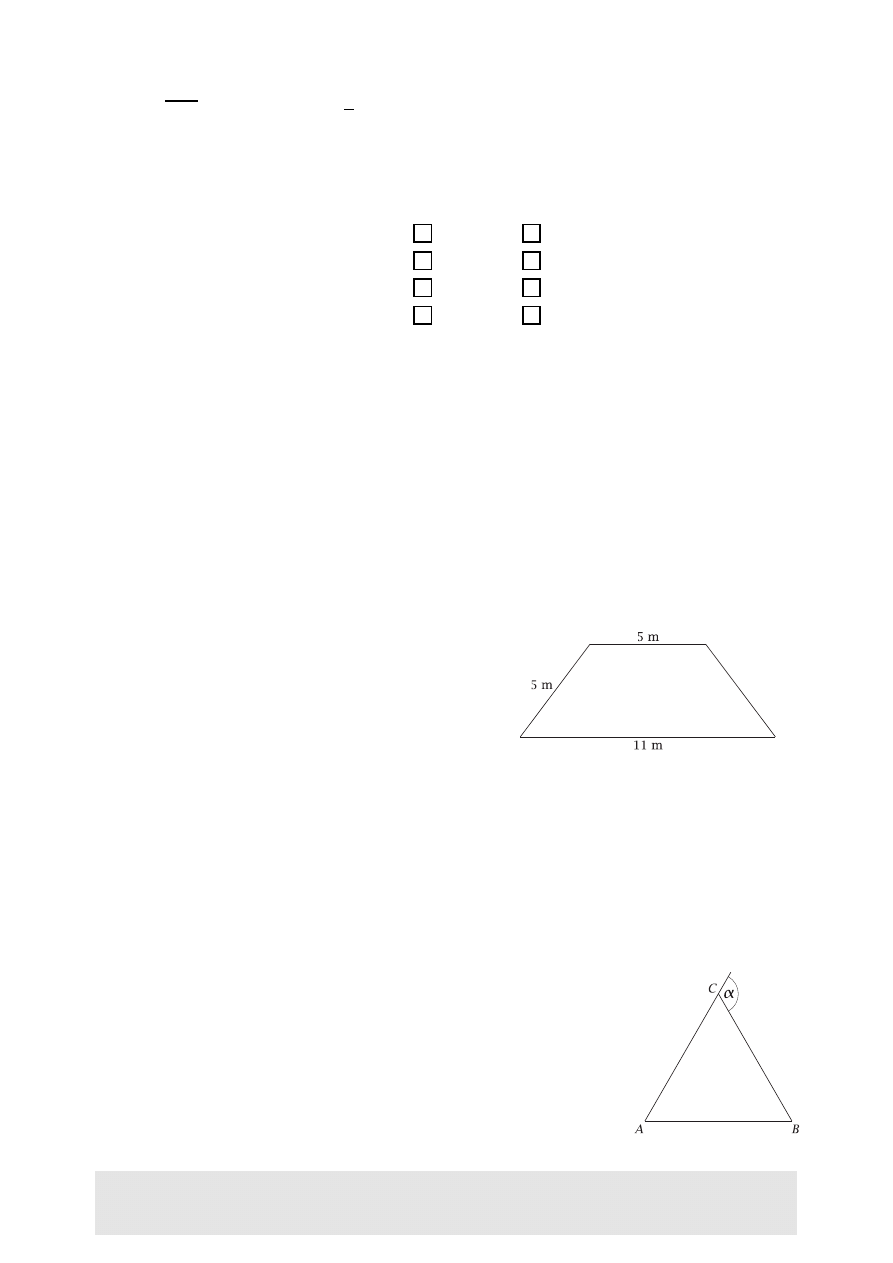
Taras w kształcie trapezu równoramiennego o wy-

miarach podanych na rysunku obok ma być wyłożony
płytkami ceramicznymi. Należy kupić tyle płytek, by ich
powierzchnia była o 10% większa niż powierzchnia ta-
rasu. Ich cena wynosi 45 zł za metr kwadratowy.

a) Ile metrów kwadratowych płytek trzeba kupić? Zapisz obliczenia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b) Ile będą kosztowały płytki kupione na wyłożenie tarasu? Zapisz obliczenia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Uzasadnij, że kąt α ma miarę równą sumie miar kątów ¾ CAB i ¾ ABC.

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 6

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

1.

Z równości a

5

=

1

b

wynika, że:

iloczyn liczb

a oraz b jest liczbą całkowitą.

TAK

NIE

liczba

a jest równa 1.

TAK

NIE

liczba

b jest równa

1
5

liczby

a.

TAK

NIE

liczby

a i b są wielkościami odwrotnie proporcjonalnymi.

TAK

NIE

2.

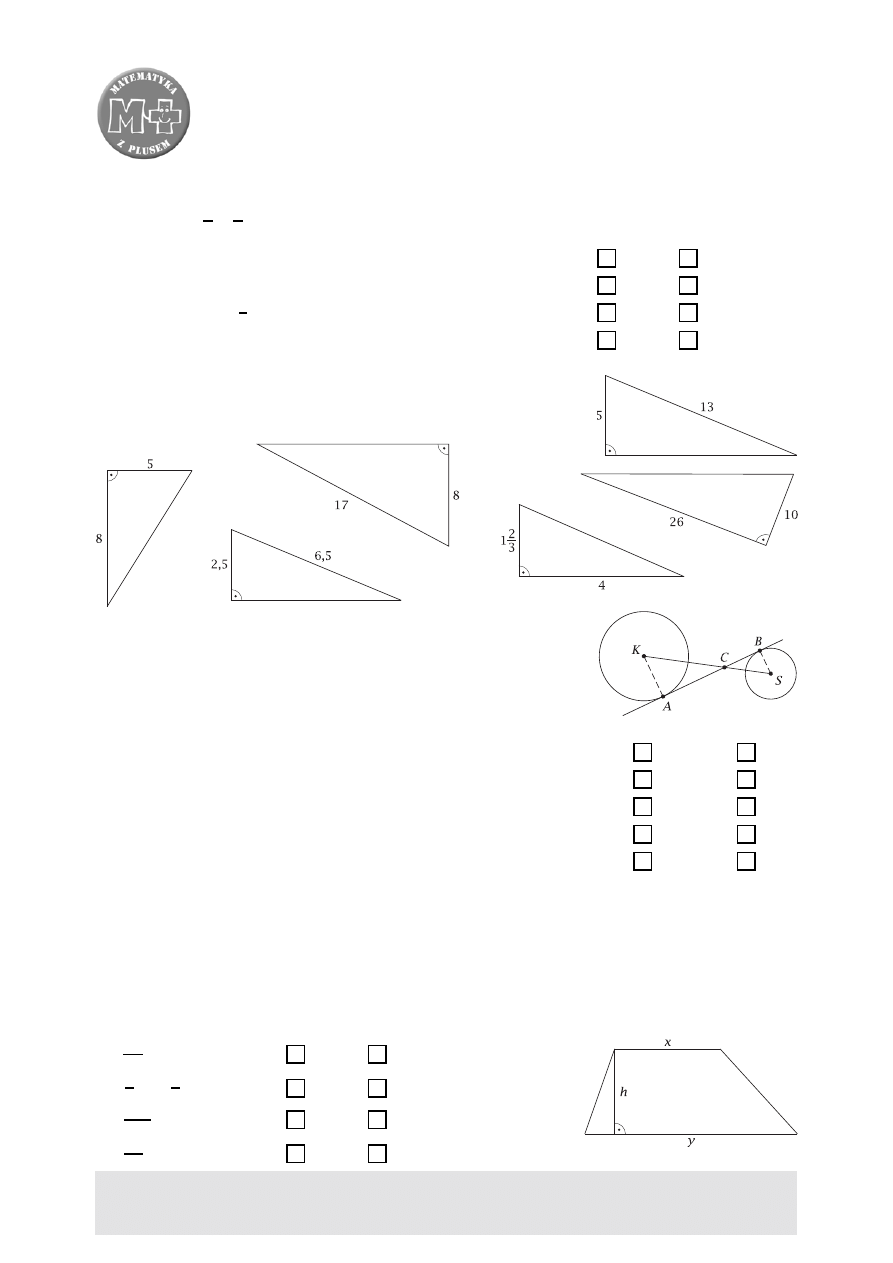
Które z trójkątów I, II, III, IV i V są podobne do trójkąta

przedstawionego na rysunku obok?

I

II

III

IV

V

3.

Punkty

A i B są punktami styczności prostej AB z okręgami

o środkach

K i S oraz promieniach równych odpowiednio 4 i 2.

Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Trójkąt

AKC jest prostokątny.

prawda

fałsz

Trójkąty

AKC i BSC są przystające.

prawda

fałsz

Trójkąty

AKC i BSC są podobne.

prawda

fałsz

Obwód trójkąta

AKC jest 2 razy większy od obwodu trójkąta BSC.

prawda

fałsz

Pole trójkąta

BSC jest 2 razy mniejsze od pola trójkąta ACK.

prawda

fałsz

4.

Dla którego zestawu danych średnia arytmetyczna wynosi 4,5 a mediana 3?

A. 5, 3, 8, 3, 2

B. 3, 10, 1, 4

C. 1, 8, 2, 11, 1, 4

D. 7, 3, 5, 3

5.

Korzystając z oznaczeń na poniższym rysunku, oceń, czy podane równości są prawdziwe.

P oznacza pole narysowanego trapezu. Wstaw znak

X

w odpowiednią kratkę.

x =

2

P

h − y

TAK

NIE

P =

1
2 xh

+

1
2 yh

TAK

NIE

h = x

+

y

2

P

TAK

NIE

y =

2

h

P − x

TAK

NIE

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

6.

Agata ma 3 kule oznaczone cyframi: 4, 5, 6. Układa je w szeregu i zapisuje powstałe liczby

trzycyfrowe. Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Kule można ułożyć tylko na 3 różne sposoby.

prawda

fałsz

Dwie spośród możliwych do ułożenia liczb są podzielne przez 15.

prawda

fałsz

Prawdopodobieństwo ułożenia liczby parzystej wynosi

2
3

.

prawda

fałsz

Prawdopodobieństwo ułożenia liczby podzielnej przez 3 wynosi

1
2

.

prawda

fałsz

7.

Forma do pieczenia ciasta ma kształt prostopadłościanu o wymiarach 2

,2 dm × 4 dm × 6 cm.

Oceń, czy podane zdania są prawdziwe. Wstaw znak

X

w odpowiednią kratkę.

Forma ma pojemność mniejszą niż 5 litrów.

TAK

NIE

Do tortownicy w kształcie walca o średnicy 30 cm i wysokości 7 cm
można wlać około 1 litra ciasta mniej.

TAK

NIE

Ciasto upieczone w tej formie można pokroić na 60 kawałków
o podstawie 4 cm

× 4 cm.

TAK

NIE

8.

Podstawka pod szklankę ma kształt trójkąta równobocznego o boku 1,5 dm. Jaki największy

promień może mieć koliste dno szklanki, by w całości zmieściło się na podstawce? Przyjmij, że

√

3

≈ 1,73. Wynik podaj z dokładnością do 1 mm. Zapisz wszystkie obliczenia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9.

Podczas szkolnego konkursu każdy zespół uczniów otrzymał 120 patyczków tej samej dłu-

gości i plastelinę. Zadanie polegało na zbudowaniu modeli sześcianów i czworościanów w jak
najkrótszym czasie i z wykorzystaniem wszystkich patyczków. Zwycięska drużyna zbudowała
15 modeli brył. Ile było wśród nich sześcianów, a ile – czworościanów? Zapisz wszystkie oblicze-
nia.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

10.

Udowodnij, że suma trzech kolejnych liczb naturalnych jest podzielna przez 3.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

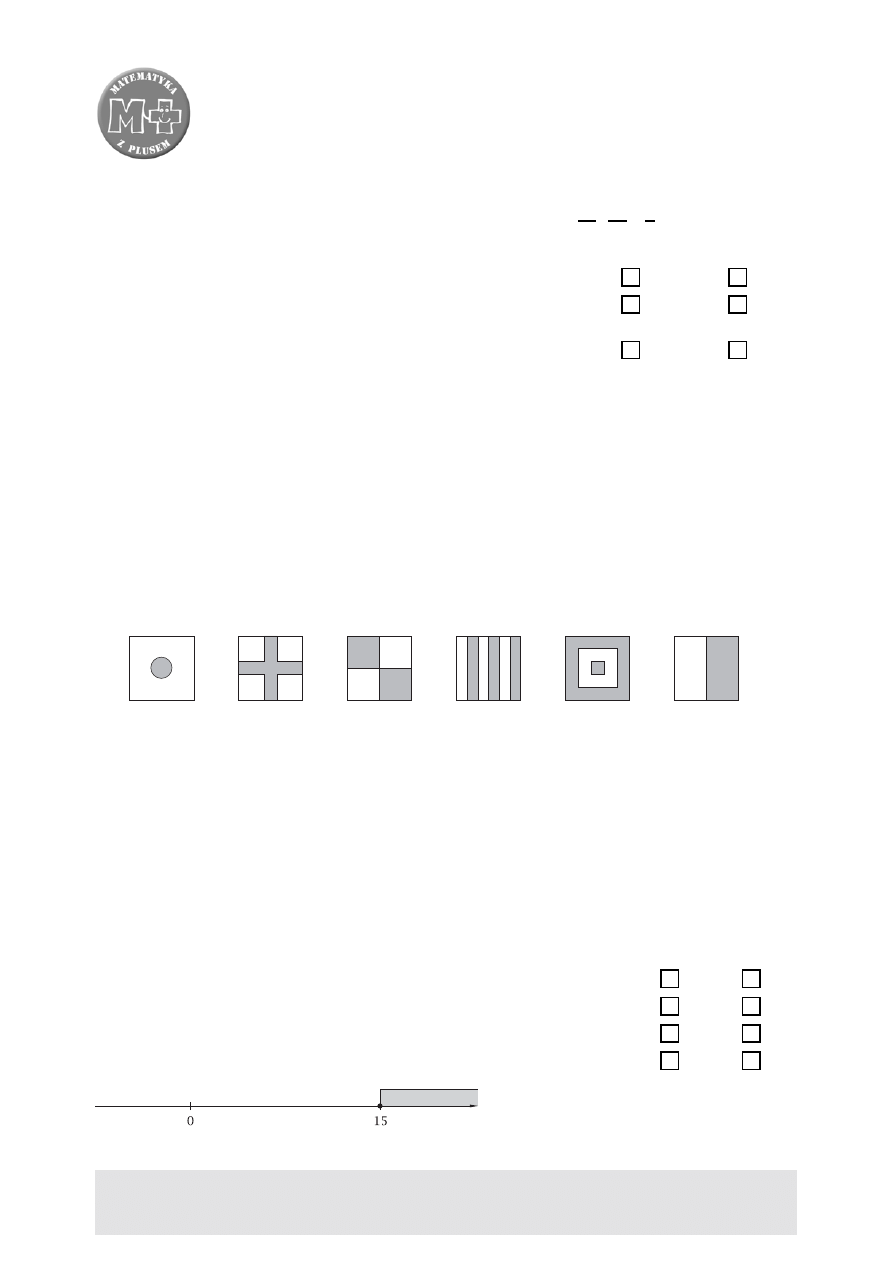
Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 7

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

1.

Z tortu wycięto kolejno trzy kawałki stanowiące odpowiednio

1

12

,

1

15

i

1
5

całego tortu. Oceń

prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Wycięte części stanowią 35% całego tortu.

prawda

fałsz

Porcja składająca się z dwóch mniejszych kawałków tortu jest
większa od trzeciego kawałka.

prawda

fałsz

Trzeci kawałek tortu jest trzykrotnie większy od drugiego ka-
wałka.

prawda

fałsz

2.

Cukiernia ma w ofercie okrągłe torty o średnicach 17 cm, 19 cm, 22 cm, 25 cm. Pudełko na

tort ma kształt graniastosłupa prawidłowego sześciokątnego, którego krawędź podstawy wynosi
12 cm. Wysokość pudełka jest większa od wysokości najwyższego z tortów. Ustal, które z ofero-
wanych rodzajów tortów zmieszczą się w całości w tym pudełku.

A. tylko tort o średnicy 17 cm
B. tylko torty o średnicy 17 cm i 19 cm

C. torty o średnicy 17 cm, 19 cm i 22 cm
D. każdy z tortów

Informacje do zadań 3 i 4.
Jacek narysował sześć znaków przedstawionych poniżej.

I.

II.

III.

IV.

V.

VI.

3.

Wypisz numery znaków, które mają co najmniej 4 osie symetrii.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.

Wypisz numery znaków, które

nie są figurami środkowosymetrycznymi.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.

Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Liczba −15 spełnia nierówność

x ≤ 15.

TAK

NIE

Liczba 15 spełnia nierówność

x ≤ 15.

TAK

NIE

Liczba 4

π spełnia nierówność x ≤ 15.

TAK

NIE

Poniższy rysunek przedstawia zbiór rozwiązań nierówności

x ≤ 15.

TAK

NIE

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

6.

Wartość wyrażenia

1

1
9

−1

+ (−7)

2

+ 0

,1 ·

5
9

0

jest równa:

A.

49

,1

B.

√

50

C.

47

8
9

D.

10

√

2

7.

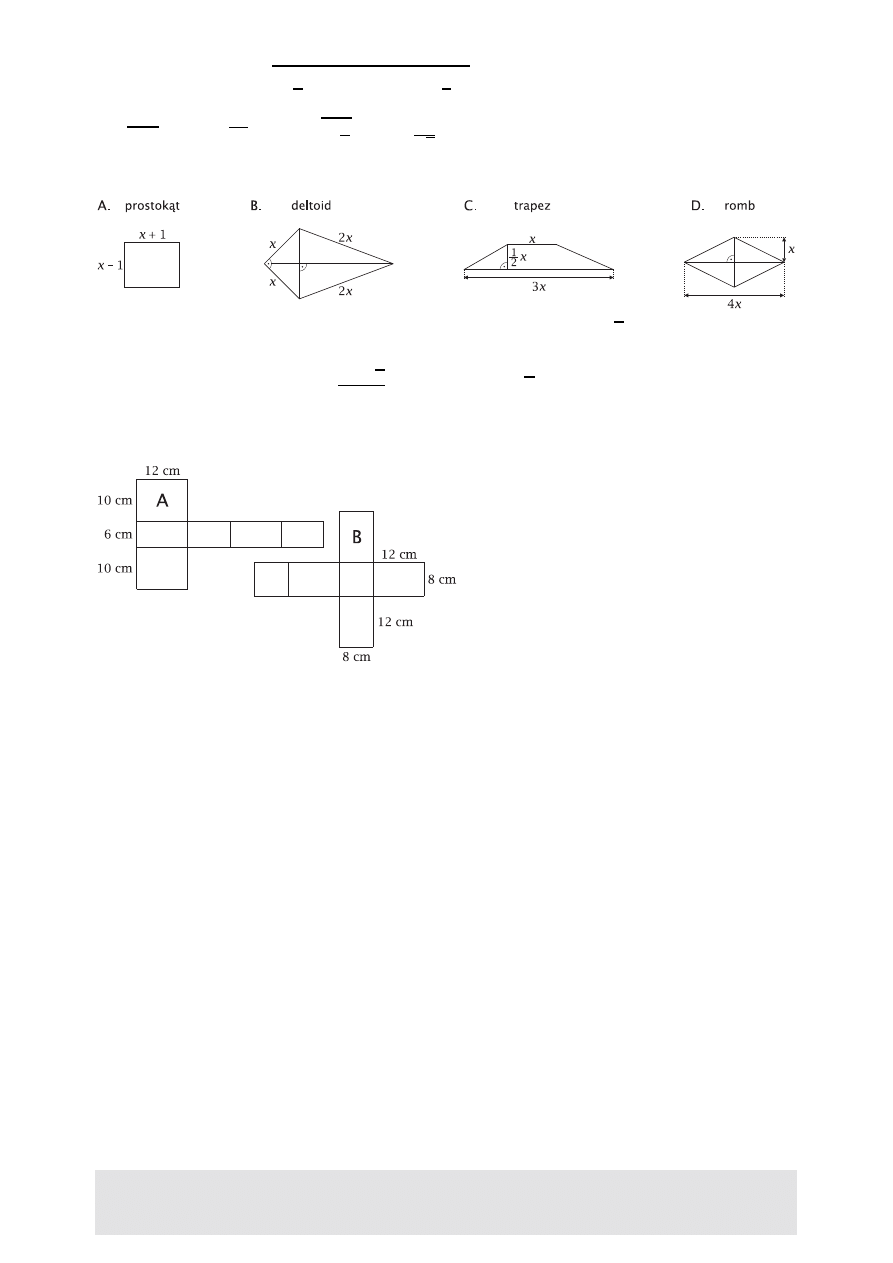
Pole kwadratu o boku

x jest równe polu czworokąta:

8.

Pole powierzchni całkowitej czworościanu foremnego wynosi 225

√

3 cm

2

. Długość krawędzi

podstawy tego czworościanu wynosi:

A. 30 cm

B. 150 mm

C.

225

√

3

4

cm

D. 562,5

√

3 mm

9.

Na rysunku poniżej przedstawiono siatki dwóch prostopadłościanów. Wykonaj odpowiednie

obliczenia i uzupełnij luki w zdaniach.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Objętość prostopadłościanu

A wynosi

. . . . . . . . . . . . . . . . . . .

cm

3

. Objętość prostopadłościanu

B wynosi

. . . . . . . . . . . . . . . . . . .

litra. Pole powierzchni prostopadłościanu

. . . . . . . . .

jest większe od pola powierzchni

(wpisz A lub B)

prostopadłościanu

. . . . . . . . .

o

. . . . . . . . .

cm

2

.

(wpisz A lub B)

10.

W ramach pracy domowej Jacek budował z kartonu modele brył. Jedną z nich był ostro-

słup prawidłowy czworokątny o krawędzi podstawy równej 16 cm i krawędzi bocznej 17 cm. Ile
cm

2

kartonu użył Jacek do wykonania siatki bryły? Dodaj 10% całkowitej powierzchni bryły na

zakładki. Wynik zaokrąglij do 1 cm

2

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Udowodnij, że pole koła wpisanego w kwadrat stanowi ponad 75% pola tego kwadratu.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

POWTÓRKI Z PLUSEM DLA KLASY III GIMNAZJUM

Zestaw zadań nr 8

Imię i nazwisko

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Klasa

. . . . . . . . . . . . . .

1.

Dany jest trójkąt ABC, gdzie A = (−7, −2), B = (−1, −2), C = (−1, 6). Oceń prawdziwość zdań.

Wstaw znak

X

w odpowiednią kratkę.

Środkiem odcinka AB jest punkt o współrzędnych (−1, 2).

prawda

fałsz

Odcinek symetryczny do odcinka AB względem osi y ma
końce w punktach A

= (−7, 2), B

= (−1, 2).

prawda

fałsz

Odcinek AC jest średnicą okręgu opisanego na tym trójkącie.

prawda

fałsz

2.

Rzucamy symetryczną kostką do gry. Siatkę tej kostki przed-

stawia rysunek obok. Prawdopodobieństwo wyrzucenia ( ) jest
równe:

A.

1
6

B.

1
2

C.

1
3

D.

1
4

3.

W trójkącie równoramiennym jeden z kątów ma miarę 70◦.

Pozostałe kąty tego trójkąta mogą mieć miary:

A. 60◦, 50◦

B. 70◦, 40◦

C. 50◦, 50◦

D. 70◦, 55◦

4.

Objętość graniastosłupa prawidłowego trójkątnego o wysokości 8 cm jest równa 200

√

3 cm

3

.

Krawędź podstawy tego graniastosłupa wynosi:

A. 5 cm

B. 20 cm

C. 15 cm

D. 10 cm

5.

Oceń prawdziwość zdań. Wstaw znak

X

w odpowiednią kratkę.

Wyrażenie 15a − (3a + 7) można zapisać w postaci 12a − 7.

prawda

fałsz

Wyrażenie

3x(4x

2

− 7x) + 8

można

zapisać

w

postaci

12x

3

− 21x

2

+ 24x.

prawda

fałsz

Wyrażenie 8a

2

b + 32ab

2

+ 56ab można zapisać w postaci

8ab(a + 4b + 7).

prawda

fałsz

Wyrażenie (3x + 5)(7 + 6x) można zapisać w postaci 21x

2

+ 30x.

prawda

fałsz

6.

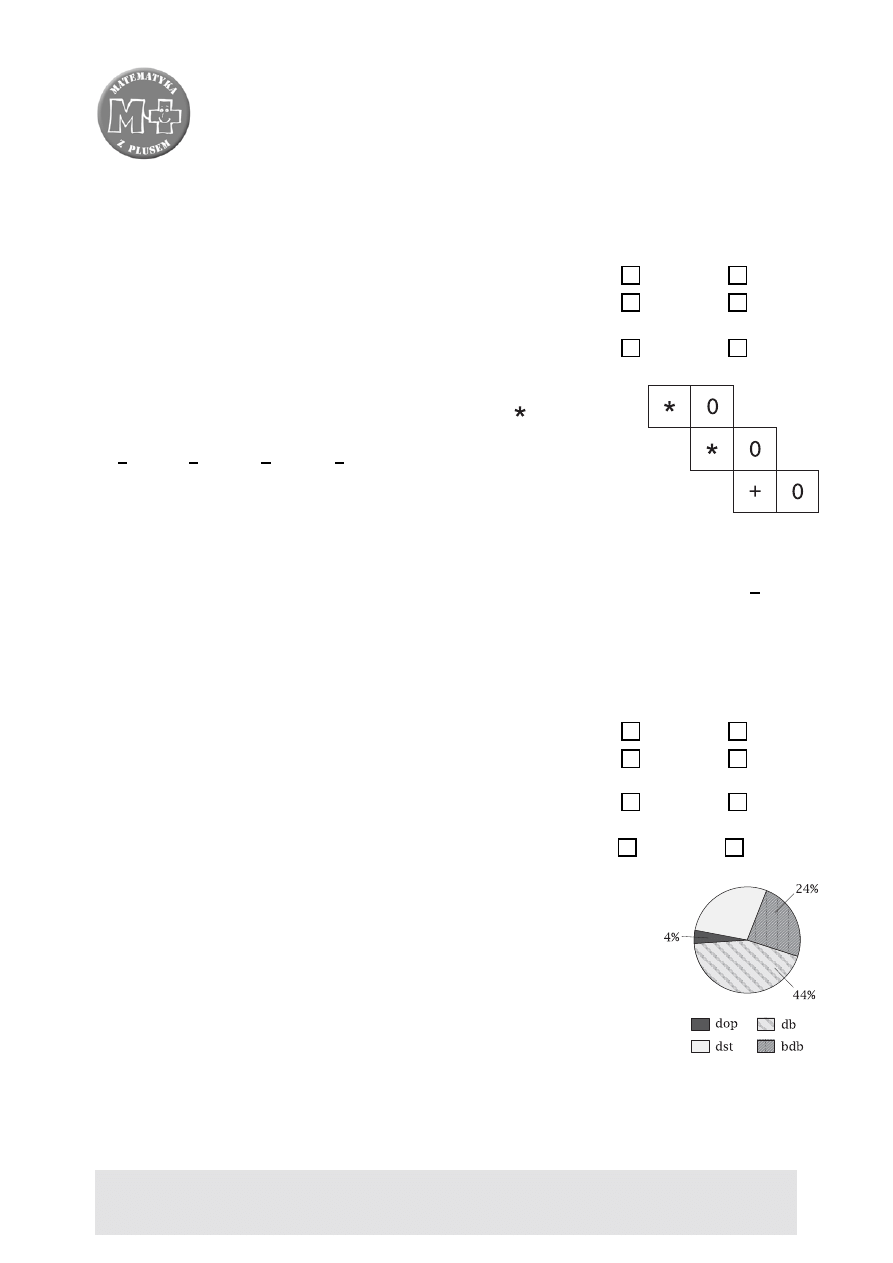
Na diagramie przedstawiono wyniki sprawdzianu w klasie dru-

giej. Wiadomo, że sześciu uczniów uzyskało ocenę bardzo dobrą,
a żaden z uczniów nie uzyskał oceny niedostatecznej ani celują-
cej. Uzupełnij zdania, tak aby były prawdziwe:

Liczba uczniów, którzy otrzymali ocenę dobrą, wynosi

. . . . . . . . . . . . . . . . .

.

Liczba uczniów, którzy pisali sprawdzian, jest równa

. . . . . . . . . . . . . . . . . . .

.

Liczba ocen dostatecznych była o

. . . . . . . . . . . . . . . . . . .

większa niż liczba

ocen dopuszczających.

Inspiracją zestawu jest książka Kalendarz gimnazjalisty —

rzetelny kurs przygotowujący do egzaminu w trzeciej klasie.

7.

Zapisz liczby w kolejności malejącej.

a = 3 · 2

2

b =

√

36 + 64

c =

3

2

12

d =

1
9

0

e = 5

5

· 15

−4

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.

Które z narysowanych brył zmieściłyby się w sześciennym pudełku o krawędzi 10 cm?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9.

W tartaku można kupić dębowe deski w kształcie prostopadłościanów o wymiarach

3 cm

× 12 cm × 2 m.

a) 1 cm

3

drewna dębowego waży 0,8 g. Ile waży jedna taka deska?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b) 1 m

3

desek dębowych kosztuje w tym tartaku 1600 zł. Ile zapłacimy za 10 takich desek?

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Odpowiedź:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

10.

Do pojemnika w kształcie walca o średnicy podstawy 50 cm, częściowo wypełnionego wodą

wlano 30 kropli olejku sosnowego. Olejek rozlał się równomiernie na powierzchni wody. Zakła-
dając, że każda kropla olejku sosnowego ma kształt kuli o średnicy równej 0,5 cm, oblicz grubość
utworzonej warstwy olejku. Wynik podaj w milimetrach.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11.

Udowodnij, że dwusieczne sąsiednich boków równoległoboku przecinają się pod kątem pro-

stym.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .