„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Teresa Piotrowska

Dokonywanie pomiarów elementów optycznych
713[07].Z3.01

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1

Recenzenci:
mgr inż. Ewa Zajączkowska
inż. Zbigniew Łuniewski



Opracowanie redakcyjne:
inż. Teresa Piotrowska



Konsultacja:
dr inż. Anna Kordowicz-Sot

Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 731[04].Z3.01
„Dokonywanie pomiarów elementów optycznych”, zawartego w modułowym programie
nauczania dla zawodu optyk-mechanik.

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2

SPIS TREŚCI

1.

Wprowadzenie

3

2.

Wymagania wstępne

4

3.

Cele kształcenia

5

4.

Materiał nauczania

6

4.1.

Pomiary właściwości materiałów optycznych

6

4.1.1.

Materiał nauczania

6

4.1.2. Pytania sprawdzające

11

4.1.3. Ćwiczenia

12

4.1.4. Sprawdzian postępów

14

4.2.

Pomiary parametrów elementów optycznych

15

4.2.1. Materiał nauczania

15

4.2.2. Pytania sprawdzające

26

4.2.3. Ćwiczenia

26

4.2.4. Sprawdzian postępów

32

4.3. Czystość optyczna

33

4.3.1. Materiał nauczania

33

4.3.2. Pytania sprawdzające

35

4.3.3. Ćwiczenia

36

4.3.4. Sprawdzian postępów

37

5.

Sprawdzian osiągnięć

38

6. Literatura

44

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3

1. WPROWADZENIE

Poradnik będzie Ci pomocny w przyswajaniu wiedzy o pomiarach elementów

optycznych: przy dobieraniu metody pomiarowej, przyrządów pomiarowych, wykonywaniu
pomiarów oraz interpretowaniu ich wyników.

W poradniku zamieszczono:

–

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,

–

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

–

materiał nauczania – wiadomości teoretyczne niezbędne do opanowania treści jednostki
modułowej,

–

zestaw pytań, abyś mógł sprawdzić, czy już opanowałeś określone treści,

–

ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,

–

sprawdzian postępów,

–

sprawdzian osiągnięć, przykładowy zestaw zadań. Zaliczenie testu potwierdzi
opanowanie materiału całej jednostki modułowej,

–

literaturę uzupełniającą.

Schemat układu jednostek modułowych

731[04].Z3.01

Dokonywanie pomiarów

elementów optycznych

731[04].Z3.02

Dokonywanie pomiarów zespołów

optycznych

731[04].Z3

Ocena jakości

wyrobów optycznych

731[04].Z3.03

Sprawdzanie kompletnego sprzętu

optycznego i optoelektronicznego

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej powinieneś umieć:

−

korzystać z różnych źródeł informacji,

−

stosować jednostki układu SI,

−

przeliczać jednostki,

−

posługiwać się podstawowymi pojęciami z zakresu: fizyki, charakteryzowania elementów
optycznych, wykonywanie elementów optycznych oraz wykonywanie podstawowych
pomiarów warsztatowych,

−

posługiwać się podstawowymi przyrządami pomiarowymi,

−

czytać schematy optyczne,

−

współpracować w grupie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

–

sklasyfikować parametry materiałów optycznych,

–

opisać i zastosować urządzenia do pomiarów właściwości materiałów optycznych,

–

zorganizować stanowisko do dokonywania pomiarów elementów optycznych,

–

dokonać pomiarów współczynnika załamania,

–

dokonać pomiarów dwójłomności,

–

sprawdzić smużystość,

–

sprawdzić pęcherzowatość,

–

określić budowę i zastosować urządzenia do pomiarów parametrów elementów
optycznych,

–

dokonać pomiarów promienia krzywizny soczewki,

–

dokonać pomiarów mocy soczewki,

–

dokonać pomiarów ogniskowej soczewki,

–

skontrolować czystość optyczną,

–

dokonać pomiarów ogniskowych soczewek,

–

sprawdzić centralność soczewek i klinowość płytek.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

6

4. MATERIAŁ NAUCZANIA

4.1. Pomiary właściwości materiałów optycznych

4.1.1. Materiał nauczania

Do konstruowania układów optycznych obarczonych małymi aberracjami niezbędny jest

określony asortyment gatunków szkieł. Parametry określające jakość szkła optycznego to:
–

współczynnik załamania n

d

,

–

dyspersja średnia (n

F

– n

C

),

–

dwójłomność,

–

absorpcja,

–

smużystość,

–

pęcherzowatość.

Pomiar współczynnika załamania

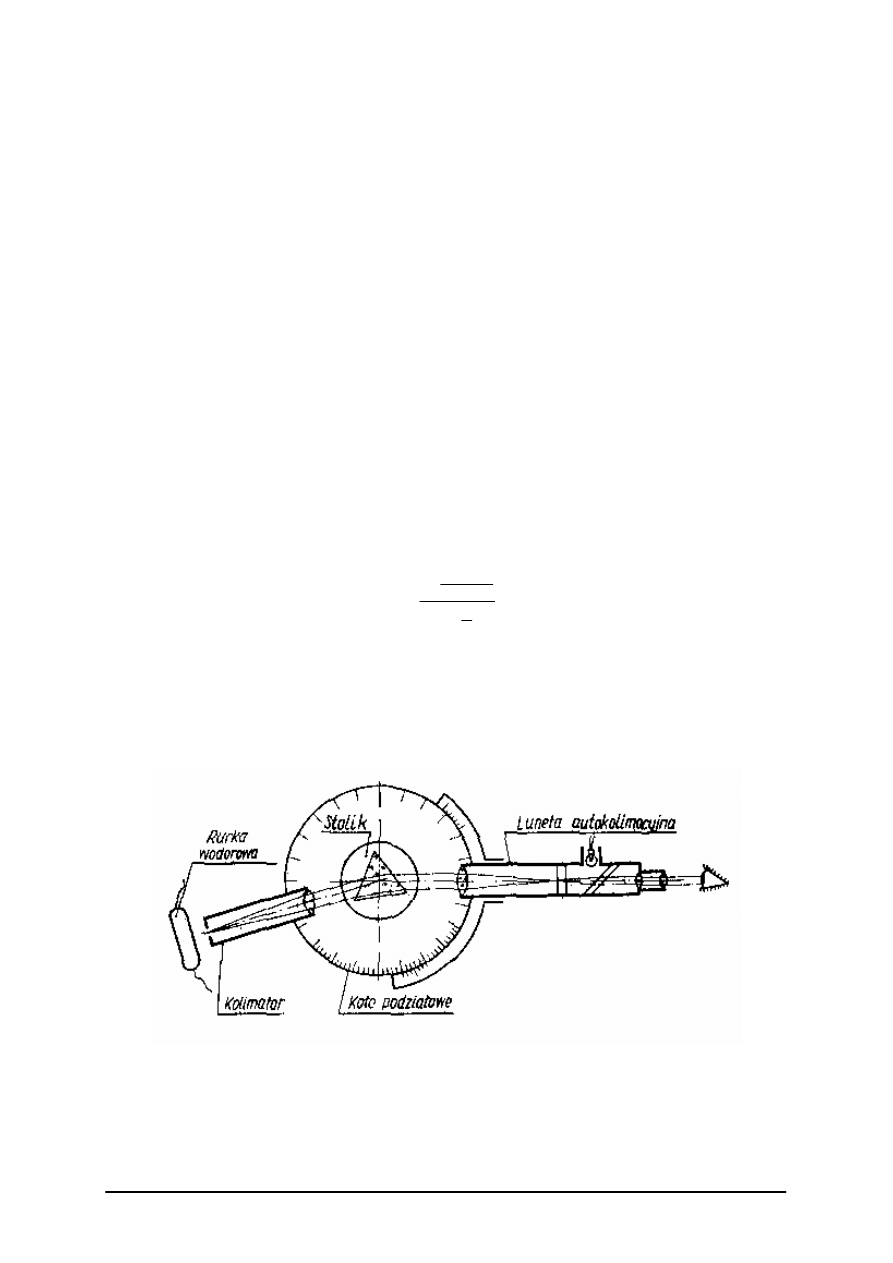
Do wyznaczania współczynnika załamania służą goniometry i refraktometry.

Za pomocą goniometru dokonujemy pomiaru kąta łamiącego θ i kata najmniejszego
odchylenia δ

min

pryzmatu wykonanego z badanego szkła, a następnie wyliczenie

współczynnika załamania wg wzoru

2

sin

2

sin

min

θ

δ

θ

+

=

n

Goniometr składa się z:

–

stałego kolimatora z krzyżem lub szczeliną,

–

stolika obrotowego,

–

lunety autokolimacyjnej, związanej sztywno z dwoma noniuszami, obracającej się dokoła
osi pionowej, przechodzącej przez środek stolika,

–

poziomego kręgu podziałowego, umożliwiającego pomiary kątów obrotu lunety.

Rys. 1. Goniometr [9, s. 314]

Z badanego szkła wykonuje się pryzmat o kącie łamiącym ok. 60° i powierzchniach

płaskich wykonanych z odchyłką N = 1/4 prążka.

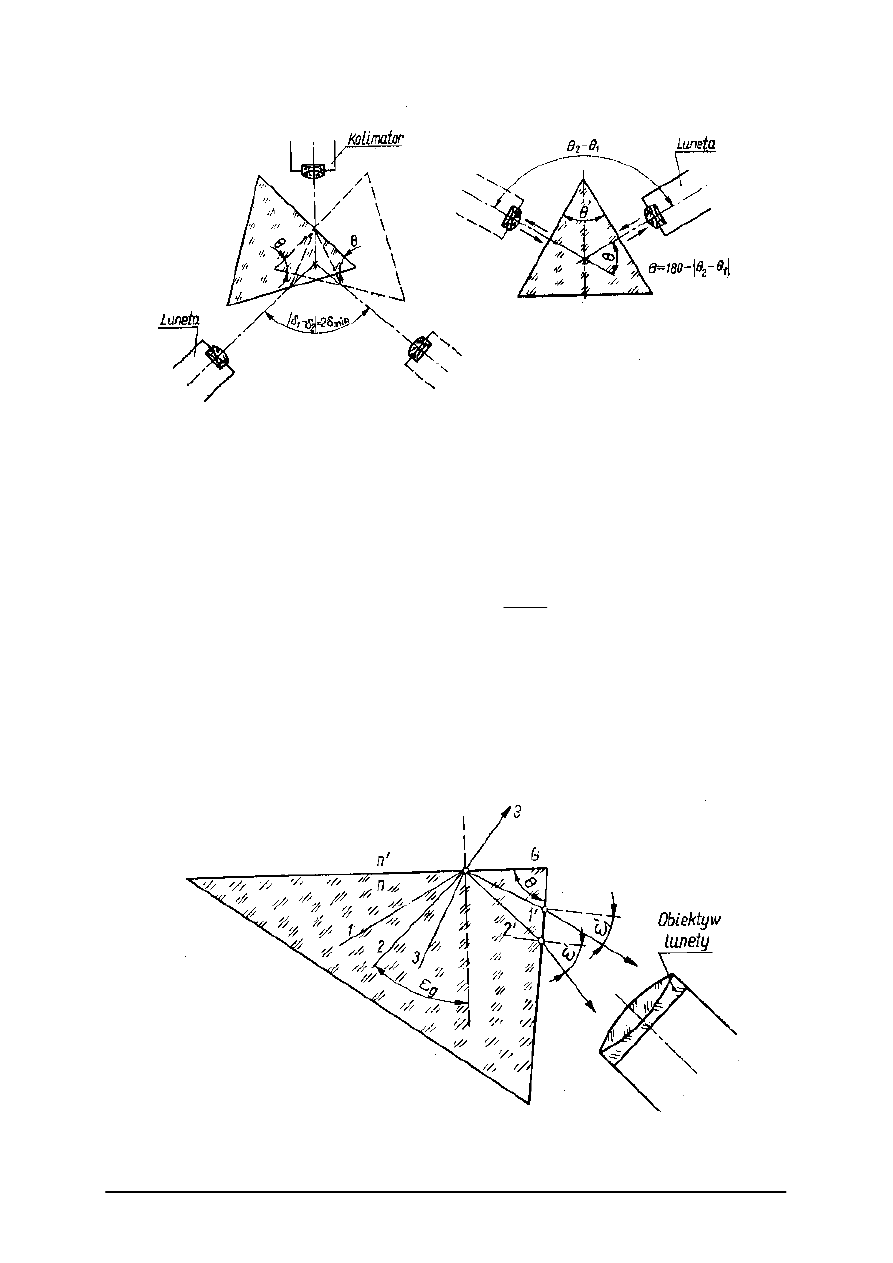
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

7

Rys. 2. Pomiar współczynnika załamania na goniometrze [9, s. 315]

Wykonany pryzmat kładziemy na stoliku goniometru i obserwując przez lunetę obraz

szczeliny kolimatora obracamy stolikiem pryzmat i wyszukujemy takie położenie, przy
którym wystąpi najmniejsze odchylenie wiązki światła przez pryzmat (rys. 2 a). Wówczas
odczytujemy kąt δ

1

położenia lunety i powtarzamy tę czynność przy symetrycznym

przestawieniu pryzmatu względem osi kolimatora i odczytujemy δ

2

. Różnica tych dwóch

odczytów jest równa podwójnemu kątowi najmniejszego odchylenia pryzmatu.

2

2

1

2

min

2

1

min

δ

δ

δ

δ

δ

δ

−

=

⇒

−

=

Następnie ustawiamy lunetę autokolimacyjną prostopadle kolejno do obu powierzchni

łamiących pryzmatu i odczytujemy kątowe położenie θ

1

i θ

2

lunety (rys. 2b). Kat łamiący

pryzmatu θ wyznaczamy z zależności.

(

)

2

1

180

θ

θ

θ

−

−

°

=

Podstawiając wartość kąta łamiącego pryzmatu θ i wartość kata najmniejszego odchylenia

δ

min

do wzoru obliczamy współczynnik załamania n badanego szkła.

Współczynnik załamania można również zmierzyć za pomocą refraktometru. Zasada

działania refraktometrów oparta jest na zjawisku całkowitego wewnętrznego odbicia.

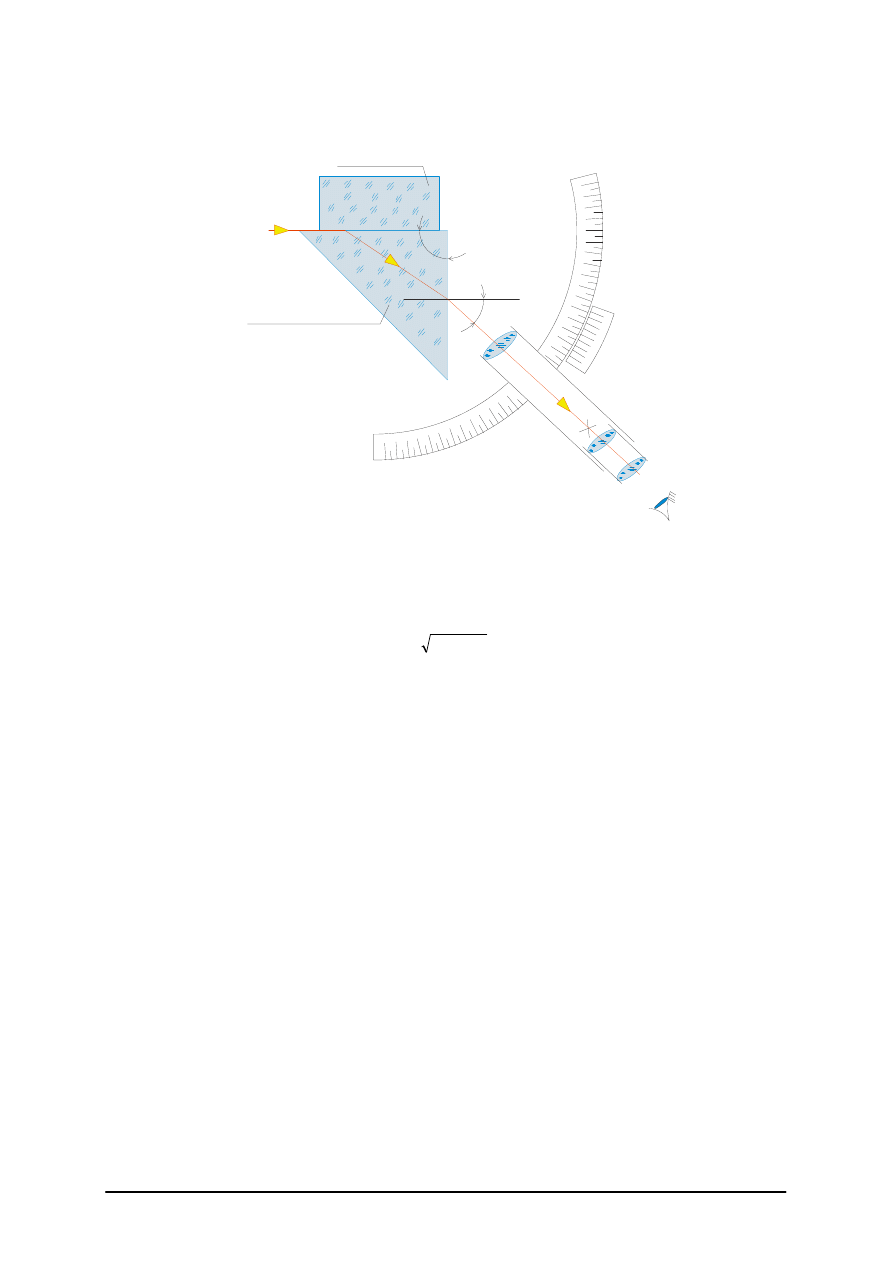
Rys. 3. Zasada działania refraktometru [9, s. 316]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

8

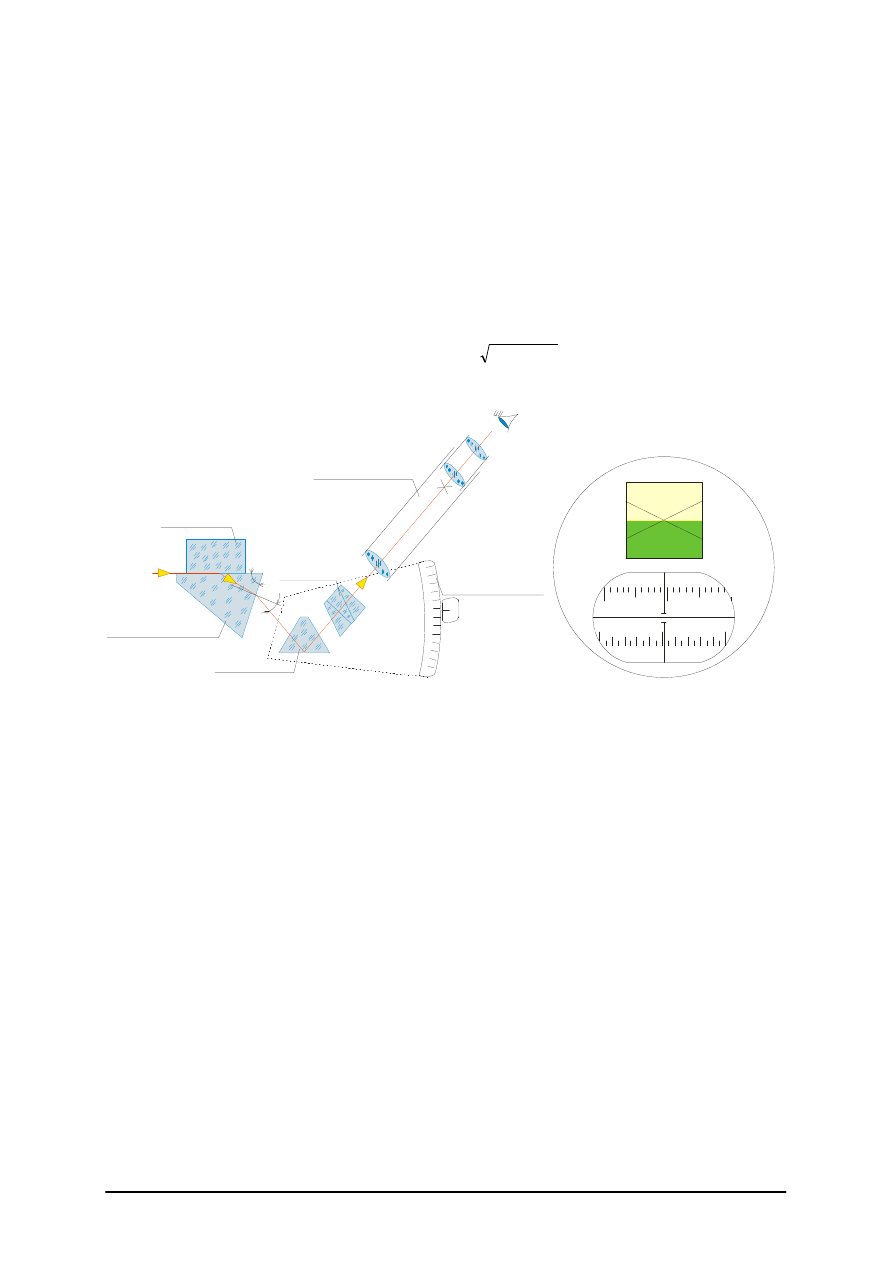
Promienie 1 przechodzą z ośrodka o współczynniku załamania n´ mniejszym i padają na

powierzchnię graniczną G pod kątem większym od granicznego ε

g

, odbiją się od tej

powierzchni i wychodzą z pryzmatu pod kątem ε’

1

. Promienie te zostają skupione

w płaszczyźnie ogniskowej obiektywu, tworząc jasne pole.

Promienie 3 padają na powierzchnię G pod kątami mniejszymi od kąta granicznego,

przechodzą do ośrodka badanego i są dla obiektywu stracone i dlatego w obiektywie druga
część pola jest ciemna.

Linię graniczną jasnego i ciemnego pola tworzą promienie padające pod kątami

granicznymi ε

g

. Linia graniczna umożliwia określenie kąta ε’. Znając współczynnik załamania

n pryzmatu pomiarowego oraz jego kąt łamiący θ, możemy wyznaczyć współczynnik
załamania n’ badanego ciała wg wzoru:

'

sin

sin

sin

cos

2

2

ε

θ

ε

θ

−

+

′

⋅

±

=

′

n

n

a)

b)

próbka szkła

n’

n

pryzmat
refraktometryczny

luneta z krzy

ż

em

pryzmat
odchylaj

ą

cy

pryzmat Amici

kompensator

skala pomiarowa

Θ

ε

‘

n

D

%

140

14

139

35

40

40

Rys. 4. Refraktometr Abbego: a) schemat układu optycznego, b) pole widzenia [opracowanie własne]

Każdy z refraktometrów składa się z czterech podstawowych zespołów :

–

pryzmat refraktometryczny,

–

pryzmat Amici (zespół pryzmatów rozszczepiających światło, a nie zmieniających
kierunku promienia żółtego), służący do achromatyzacji linii granicznej między polem
jasnym i ciemnym,

–

lunetka z krzyżem,

–

skala pomiarowa.
W refraktometrze Abbego znajduje się jeszcze pryzmat odchylający związany sztywno ze

skalą pomiarową, najczęściej wyskalowaną w jednostkach współczynnika załamania.

Badaną próbkę kładziemy płaską wypolerowaną stroną na powierzchni pomiarowej

pryzmatu refraktometrycznego. Pomiędzy te powierzchnie wprowadzamy ciecz immersyjną
o współczynniku załamania większym od badanej substancji. Obrotem pryzmatu
odchylającego naprowadzamy linię graniczną pola jasnego i ciemnego na środek krzyża
lunety, a współczynnik załamania odczytujemy ze skali (rys. 4 b).

Jeśli pryzmat oświetlimy światłem białym, to linia graniczna w lunecie będzie

zabarwiona. Obrotem pryzmatu Amici możemy skompensować chromatyzm linii granicznej.
Dokładność pomiaru jest rzędu 0,0002, a zakres pomiarowy wynosi od n = 1,3 do n = 1,7.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

9

Współczynnik załamania możemy również zmierzyć za pomocą refraktometru

Pulfricha.

n’

n

Θ

ε

‘

pryzmat
refraktometryczny

próbka szkła

Rys. 5. Zasada działania refraktometru Pulfricha [opracowanie własne]

Refraktometr ten od refraktometru Abbego różni się tym, że pryzmat refraktometryczny

posiada kąt łamiący θ wynosi 90° i współczynnik załamania wyraża się wzorem:

ε

′

−

=

′

2

2

sin

n

n

Refraktometr ten nie ma pryzmatu kompensującego Amici, gdyż pracuje w świetle

monochromatycznym, a elementem ruchomym jest luneta związana na sztywno z kręgiem
kątowym umożliwiającym wyznaczenie kątów ε’.

Refraktometrem tym możemy również dokonać pomiaru współczynnika załamania cieczy

i daje dokładność 0,0001.

Pomiar dyspersji średniej (n

F

– n

C

)

Do pomiaru dyspersji średniej używamy refraktometru Abbego. Czynności w czasie

pomiaru są takie jak przy pomiarze współczynnika załamania.

Odczytując kąt obrotu pryzmatu Amici i posługując się tablicą załączoną do

refraktometru wyznaczamy dyspersję średnią n

F

– n

C

badanej substancji.

Pomiar dwójłomności

Dwójłomność szkła jest wywołana naprężeniami wewnętrznymi powstałymi w procesie

studzenia. Miarą dwójłomności jest różnica dróg optycznych (w nm) dla promieni
zwyczajnego i nadzwyczajnego w warstwie o grubości 1 cm. Dwójłomność mierzymy za
pomocą polaryskopu.

Pomiar współczynnika absorpcji

Współczynnik absorpcji szkła optycznego jest to stosunek strumienia światła białego

pochłoniętego w warstwie szkła o grubości 1 cm do strumienia światła wpadającego do tej
warstwy. Absorpcję szkła możemy mierzyć z użyciem urządzeń fotometrycznych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

10

Rys. 6. Przepuszczalność światła przez warstwę szkła [9, s. 163]

Na materiał optyczny (szkło) o grubości d pada strumień świetlny Ф, a opuszcza układ

strumień Ф’. Stosunek strumienia światła przechodzącego Ф’ do padającego Ф nazywamy
przepuszczalnością T danego układu optycznego:

φ

φ′

=

T

Znając przepuszczalność szkła, możemy obliczyć absorpcję z zależności 1/T.

Aby wyznaczyć strumień świetlny Ф należy dokonać pomiaru natężenia oświetlenia E za

pomocą fotometru i wyznaczyć z wzoru

0

0

S

E

S

E

×

=

⇒

=

φ

φ

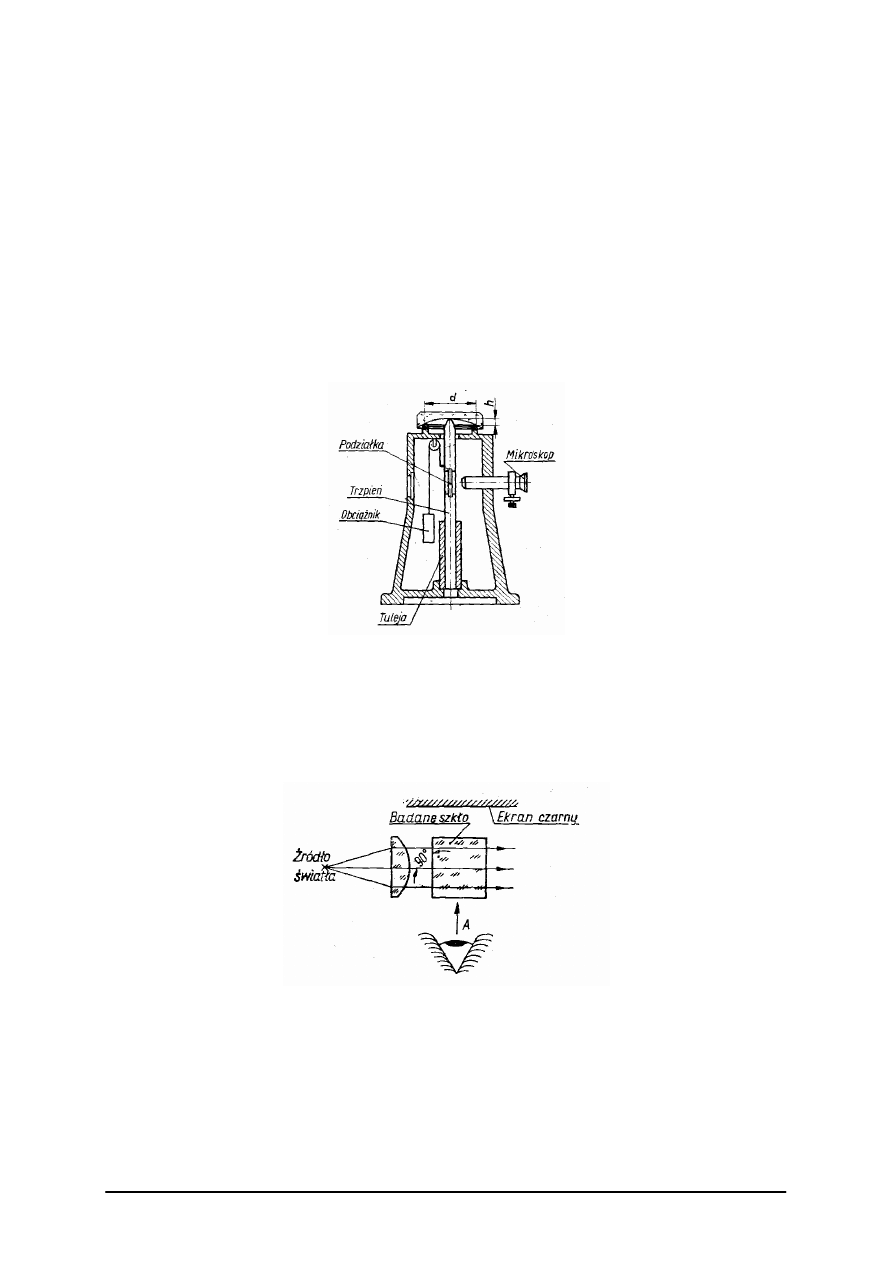
Kontrola smużystości

Smugi – nitkowe pasma w szkle, w których współczynnik załamania różni się od

współczynnika załamania masy szklanej. Powstaje w procesie topienia masy szklanej
i spowodowana jest niejednorodnością chemiczną niektórych warstw, posiadających wskutek
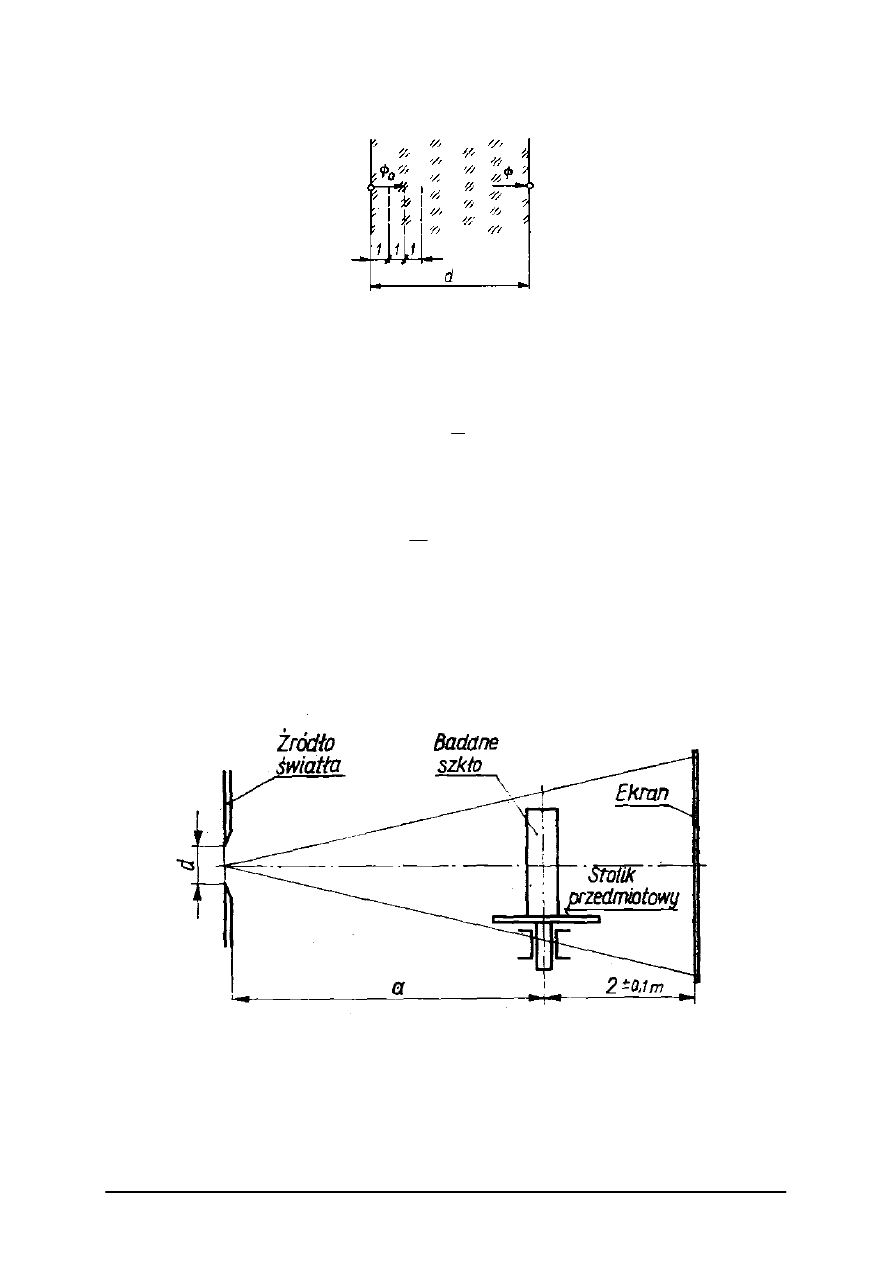
tego odmienny współczynnik załamania. Wykrywamy je w układzie diafragma, źródło
światła, ekran (rys. 7).

Rys. 7. Schemat urządzenia do sprawdzania smużystości w szkle [9, s. 321]

Stanowisko to nazywamy cienioskopem. Jeśli w biegu promieni znajdzie się smuga, to

spowoduje ona odchylenie przechodzących promieni i na ekranie powstanie cień. Widoczność
jego zależy od stosunku średnicy d źródła światła do jego odległości a od osi obrotu stolika

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

11

przedmiotowego. Im mniejszy jest ten stosunek, tym drobniejsze smugi uwidocznią się na
ekranie w postaci cienia.

Norma ustala 3 kategorie smużystości w zależności od liczby kierunków przeglądania

szkła.

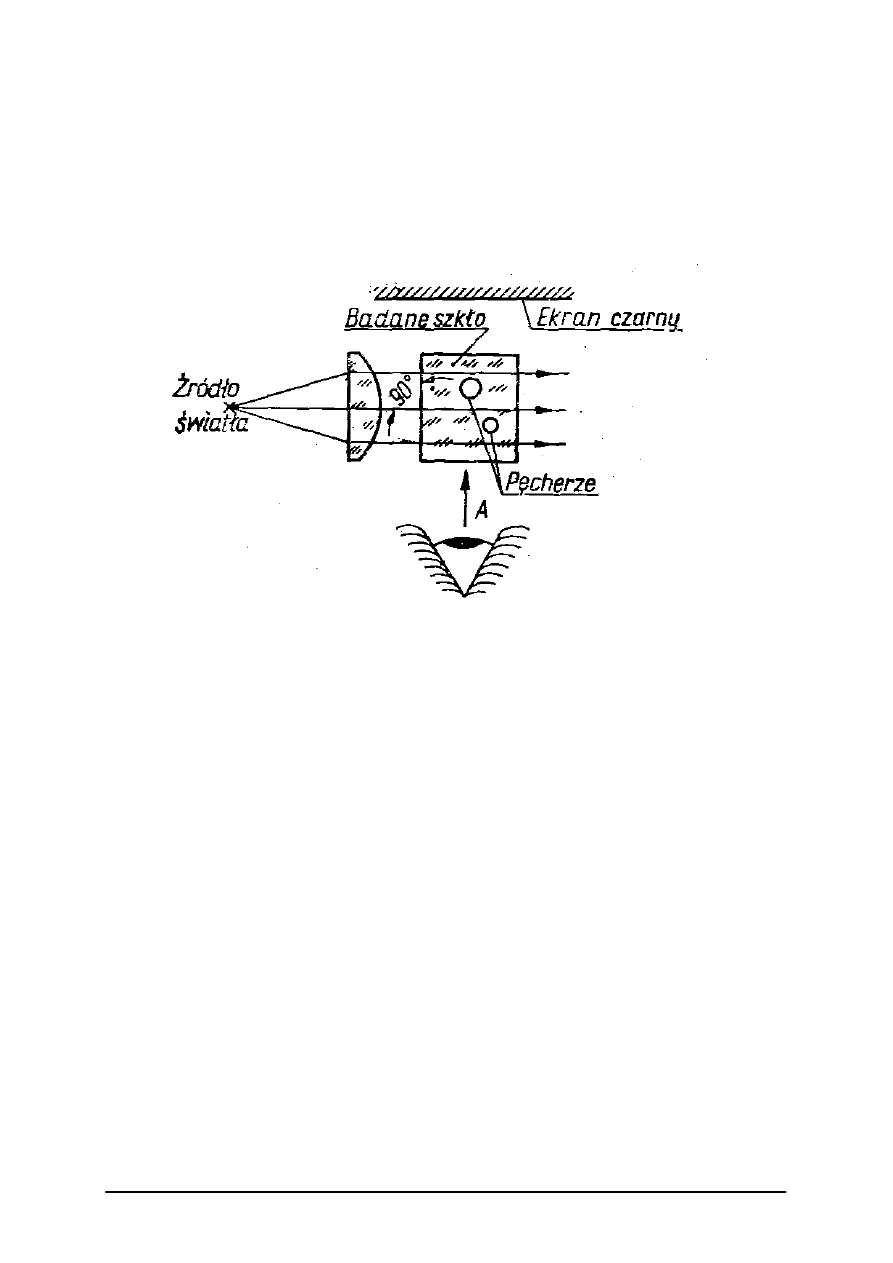
Kontrola pęcherzowatości

Pęcherze i obce wtrącenia w szkle, wykrywamy w układzie pokazanym na rysunku 8.

Rys. 8. Schemat stanowiska do kontroli pęcherzowatości [9, s. 322]

Przy silnym oświetleniu badanej próbki szkła prostopadle do kierunku obserwacji na

ciemnym tle pęcherze i kamienie są widoczne jako świecące punkty. Ich wymiary ocenia się
przez porównanie z wzorcowymi pęcherzami o znanych wymiarach.

Norma przewiduje 8 kategorii pęcherzowatości w zależności od wymiarów pęcherzy i 7

klas w zależności od ich liczby w jednostce objętości masy szklanej.

Kategorię ustalamy na podstawie szóstego co do wielkości pęcherza. Klasę

pęcherzowatości określa się średnią ilością pęcherzy w 1 kg szkła z danego wytopu.

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Jakimi przyrządami można zmierzyć współczynnik załamania?

2.

Jak zbudowany jest goniometr?

3.

W jaki sposób mierzymy dyspersję średnią?

4.

W jaki sposób mierzymy współczynnik absorpcji?

5.

W jaki sposób mierzymy dwójłomność?

6.

W jaki sposób sprawdzamy pęcherzowatość?

7.

W jaki sposób sprawdzamy smużystość w szkle?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12

4.1.3. Ćwiczenia

Ćwiczenie 1

Zmierz współczynnik załamania szkła za pomocą goniometru.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy lunety
autokolimacyjnej i kolimatora,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące pryzmatu załamującego
i współczynnika załamania światła,

3)

odczytać kąty najmniejszego odchylenia w dwóch położeniach lunety δ

1

i δ

2

,

4)

obliczyć kąt najmniejszego odchylenia pryzmatu δ

min

,

5)

obliczyć kąt łamiący pryzmatu θ,

6)

obliczyć współczynnik załamania szkła n z jakiego jest wykonany pryzmat.

Wyposażenie stanowiska pracy:

−

goniometr,

−

instrukcja obsługi goniometru,

−

pryzmat załamujący do pomiaru,

−

kalkulator.

Ćwiczenie 2

Wyznacz współczynnik załamania szkła za pomocą refraktometru Abbego.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy refraktometru
Abbego,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące współczynnika załamania
światła,

3)

wyznaczyć współczynnik załamania szkła wskazanej próbki.

Wyposażenie stanowiska pracy:

−

refraktometr Abbego,

−

ciecz immersyjna,

−

instrukcja obsługi refraktometru Abbego,

−

próbka szkła.

Ćwiczenie 3

Sprawdź dwójłomność w bloku szkła, soczewce wykonanej ze szkła mineralnego

i organicznego, elemencie optycznym zamocowanym w oprawie.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące dwójłomności,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

13

2)

wyszukać w materiałach dydaktycznych informacje dotyczące polaryskopu,

3)

wyznaczyć i narysować naprężenia we wskazanych próbkach,

4)

określić kategorię dwójłomności.

Wyposażenie stanowiska pracy:

−

polaryskop,

−

instrukcja obsługi polaryskopu,

−

próbki do badań: blok szkła, soczewka ze szkła mineralnego, soczewka ze szkła
organicznego, elementy optyczne w oprawach,

−

normy.

Ćwiczenie 4

Skontroluj smużystość wskazanych próbek.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące sprawdzania smużystości
szkła,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące smug w materiałach
optycznych,

3)

skontrolować smużystość wskazanych próbek szkła.

4)

określić kategorię i klasę smużystości.

Wyposażenie stanowiska pracy:

−

urządzenie do sprawdzania smużystości,

−

instrukcja obsługi urządzenia do sprawdzania smużystości,

−

próbki szkła,

−

normy.

Ćwiczenie 5

Sprawdź pęcherzowatość wskazanych próbek szkła.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pęcherzowatości

,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące stanowiska do kontroli
pęcherzowatości,

3)

sprawdzić wskazane próbki szkła,

4)

określić klasy i kategorie pęcherzowatości badanych próbek szkła.

Wyposażenie stanowiska pracy:

−

układ do sprawdzania pęcherzowatości,

−

instrukcja obsługi urządzenia do sprawdzania pęcherzowatości,

−

próbki szkła,

−

normy.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

14

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

opisać budowę goniometru?

2)

opisać budowę refraktometru Abbego?

3)

określić dwójłomność?

4)

określić smużystość?

5)

określić pęcherzowatość?

6)

zdefiniować współczynnik absorpcji?

7)

sklasyfikować metody pomiaru współczynnika załamania szkła?

8)

dokonać pomiaru współczynnika załamania?

9)

dokonać pomiaru dyspersji?

10)

dokonać pomiaru dwójłomności?

11)

dokonać pomiaru współczynnika absorpcji?

12)

dokonać kontroli smużystości?

13)

dokonać kontroli pęcherzowatości?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

15

4.2.

Pomiary parametrów elementów optycznych

4.2.1.

Materiał nauczania

Pomiar płaszczyzn

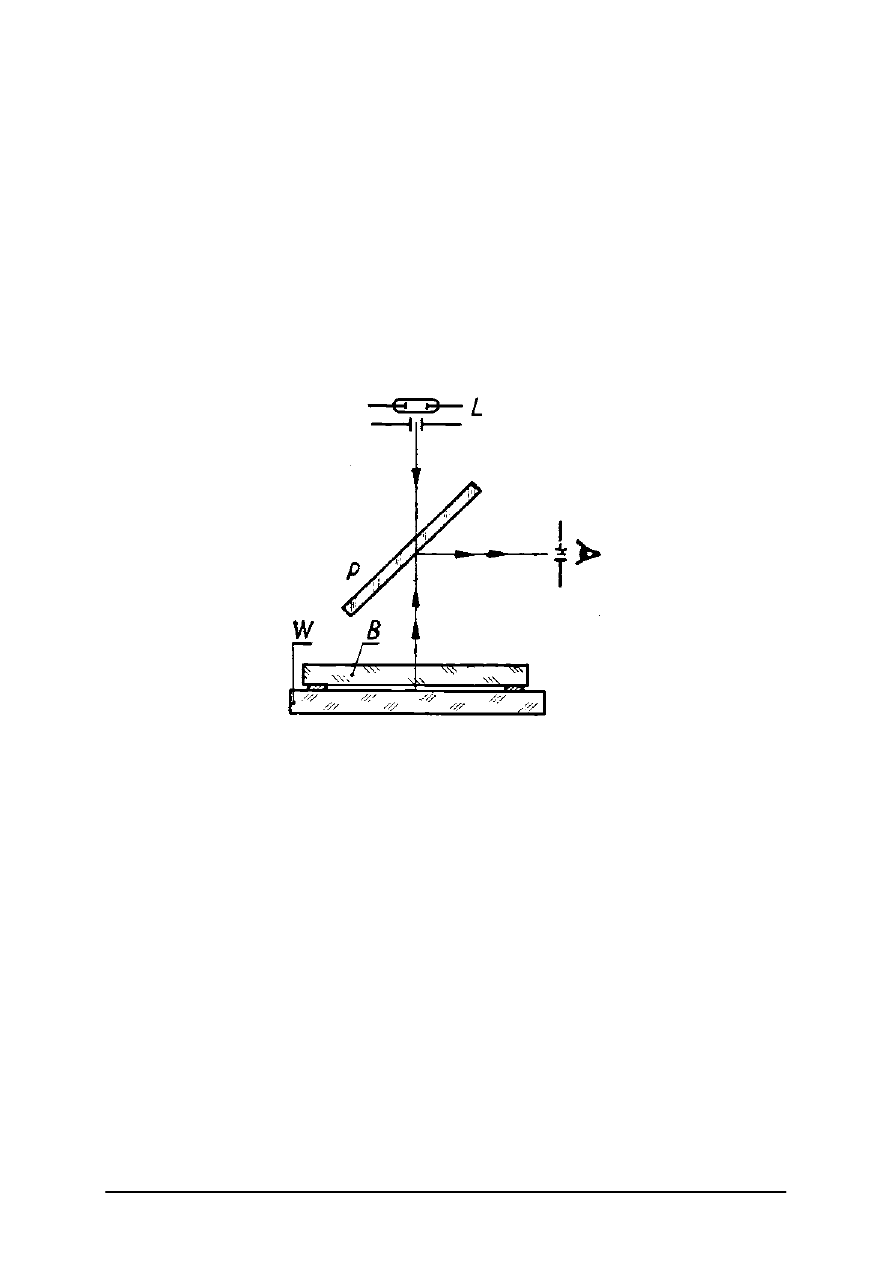
W masowej produkcji jakość wykonania powierzchni płaskich o średnicy do 200 mm

sprawdzamy za pomocą szklanych sprawdzianów interferencyjnych. Nakładając sprawdzian
na badaną powierzchnię, obserwujemy prążki interferencyjne tworzące się w cienkiej
warstewce powietrza między stykającymi się powierzchniami szklanymi. Kształt i barwa
prążków pozwalają nam na ocenę jakości badanej powierzchni.

Do badania powierzchni płaskich używamy interferometrów, których działanie opiera się

na porównaniu badanych powierzchni z powierzchniami wzorcowymi.

Rys. 9. Interferometr na płycie szklanej [2, s. 209]

Na rysunku 9 przedstawiono najprostszy typ interferometru. Na płycie szklanej

W posiadającej wzorcową powierzchnię górną kładziemy kawałeczki bibułki, a na nich
badaną płytkę B. Obie płytki oświetlamy za pomocą źródła światła monochromatycznego L,
przed którym znajduje się diafragma z okrągłym otworkiem. Promienie wychodzące
z okrągłego oświetlonego otworka diafragmy przechodzą przez płytkę płaskorównoległą P
nachyloną pod kątem 45° do powierzchni wzorcowej. Promienie odbite od dolnej powierzchni
badanej płytki i górnej wzorca interferują ze sobą, odbijają się od płytki P i kierują się do oka
obserwatora.

Wzorzec W powierzchni płaskiej wykonujemy z twardego szkła, dobrze odprężonego,

albo jeszcze lepiej z kwarcu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

16

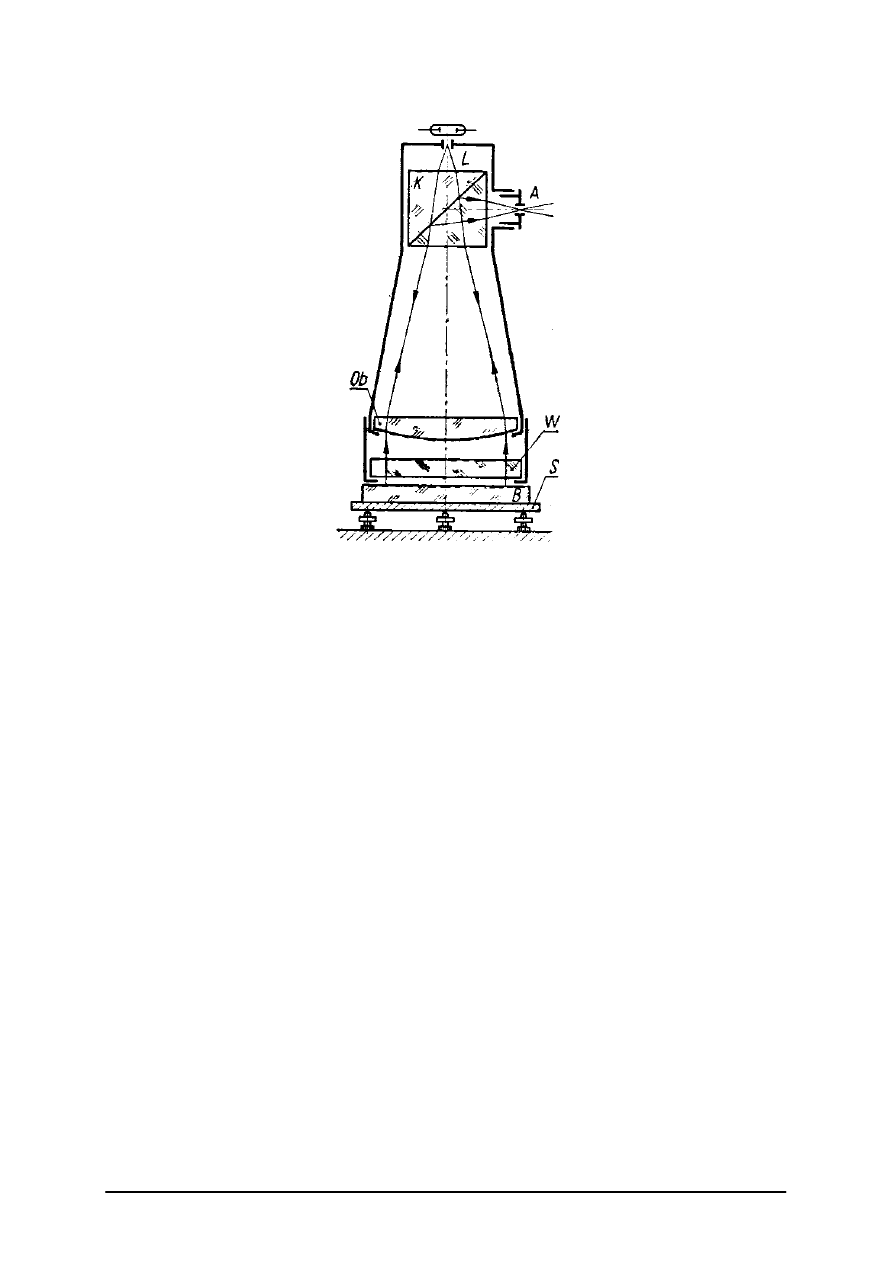
Rys. 10. Interferometr warsztatowy [2, s. 209]

Na rysunku 10 przedstawiono schematycznie typ interferometru warsztatowego, za

pomocą którego możemy obserwować prążki jednakowej grubości. Badaną płaszczyznę B
kładziemy na regulowanym trzema śrubami stoliku S. Stolik może być podnoszony do góry
w kierunku wzorcowej powierzchni klinowego sprawdzianu W. Monochromatyczne światło
wychodzące z otworka oświetlonego lampą L przechodzi szklany sześcian K składający się
z dwóch sklejonych pryzmatów prostokątnych, z których jeden na swej ściance
przeciwprostokątnej ma nałożoną częściowo przezroczystą cienką warstwę srebra, aluminium
lub chromu.

Ponieważ źródło światła L znajduje się w płaszczyźnie ogniskowej obiektywu Ob, więc

na wzorzec W i płytkę badaną B padają pęki promieni równoległych, które po odbiciu skupią
się w punkcie A, w którym znajduje się źrenica oka obserwatora. Przez mały otworek A
obserwujemy powstałe między powierzchniami W i B prążki jednakowej grubości. Prążki te
będą . proste w tym przypadku, kiedy badana powierzchnia B stanowi płaszczyznę.
Zakrzywienie prążków, wyrażone w ułamku odległości między prążkami charakteryzuje
kształt badanej powierzchni. Interpretacja prążków została omówiona w poradniku
„Charakteryzowanie elementów optycznych” – moduł Z1.01.

Sprawdzian W powinien być wykonany z największą, technicznie osiągalną

dokładnością, przy czym jego promień nie powinien być mniejszy niż 10 km.

W celu otrzymania prążków musimy między powierzchniami płytki wzorcowej i badanej

wytworzyć klin powietrzny o bardzo małym kącie łamiącym. W celu łatwego i szybkiego
otrzymania obrazu interferencyjnego należy wyjąć oprawkę z otworkiem A i włożyć na jej
miejsce dodatni okular, który wraz z obiektywem Ob będzie stanowił lunetę typu Keplera.
Przez okular ten możemy obserwować powstałe w płaszczyźnie ogniskowej obiektywu,
autokolimacyjne obrazy otworka L znajdującego się także w płaszczyźnie ogniskowej
obiektywu Ob. Działając śrubami stolika interferometru doprowadzamy do pokrycia się ze

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

17

sobą autokolimacyjnych obrazów otworka L utworzonych na skutek odbicia się promieni od
dolnej powierzchni wzorca i górnej płytki badanej.

Po wykonaniu tej operacji powierzchnia sprawdzana i wzorcowa są już prawie

równoległe i wtedy mały ruch jednej ze śrub regulacyjnych stolika wystarcza do wytworzenia
klina powietrznego, w którym powstaną prążki równoległe do jego krawędzi łamiącej.
W klinie przekroje o jednakowej grubości są równoległe do krawędzi kąta łamiącego. Przez
zmniejszenie kąta łamiącego klina powietrznego za pomocą śrub stolika możemy
„rozciągnąć” prążki interferencyjne jednakowej grubości, co polepszy nam warunki pomiaru.

Należy podkreślić, że otworek oświetlający powinien mieć większą średnicę niż otworek

A. Obraz interferencyjny jest najbardziej kontrastowy, gdy otworek A „wycina” wspólne pole
obrazów otworka oświetlającego, utworzonych przez powierzchnie wzorcową i badaną.

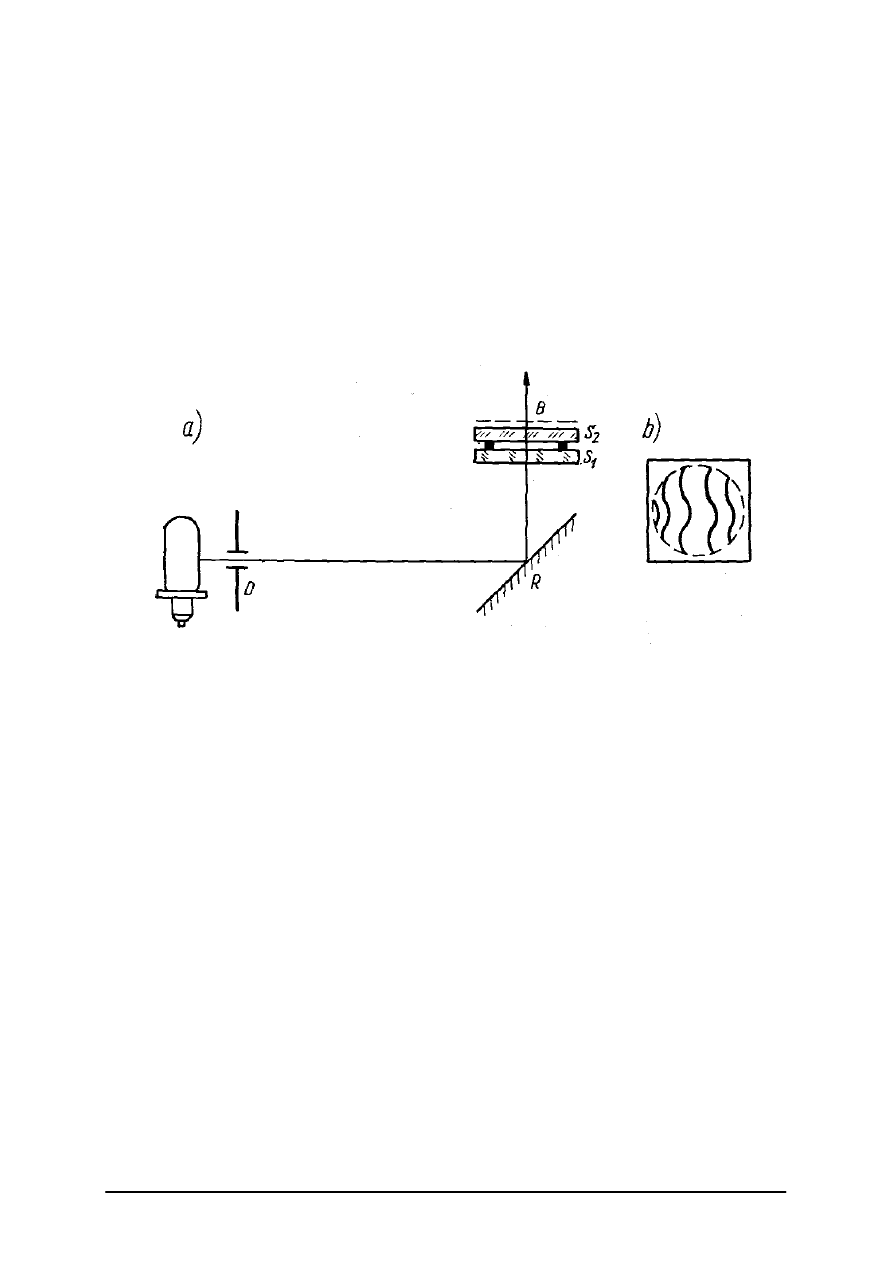
Rys. 11. Interferometr do sprawdzania płaszczyzn [2, s. 212]

Do sprawdzania bardzo dokładnie wykonanych płaskich powierzchni optycznych

wykorzystuje się zjawisko tzw. wielopromieniowej interferencji, w którym biorą udział
promienie wielokrotnie odbite od powierzchni płytki płaskorównoległej i przy której
otrzymuje się większą, niż w interferencji dwupromieniowej, kontrastowość prążków.

Na rys. 11a przedstawiono schemat optyczny interferometru do sprawdzania płaszczyzn,

za pomocą którego można osiągnąć dokładność sprawdzenia równą 0,01 szerokości prążka.

Lampa rtęciowa oświetla niewielki otwór diafragmy D. Światło po odbiciu od zwierciadła

R przechodzi przez badane płytki szklane S, i S

2

. Płytki są do siebie zwrócone sprawdzanymi

powierzchniami, które dla wyrównania natężeń promieni odbitych i przechodzących, są
pokryte częściowo przepuszczającymi warstwami zwierciadlanymi, najczęściej srebra ze
względu na małą absorpcję.

Między sprawdzanymi powierzchniami umieszcza się trzy małe przekładki z folii

o grubości równej około 0,01 mm.

Interferencja promieni odbywa się w warstewce powietrza między sprawdzanymi

powierzchniami.

Promień padający na sprawdzane płytki ulega po wielokrotnych odbiciach rozdzieleniu na

dużą ilość promieni prawie równolegle wychodzących z płytki S

2

, które ze sobą interferują.

Ponieważ prążki interferencyjne są wystarczająco pstre zarówno w warstewce powietrza
między powierzchniami sprawdzanymi jak i w pewnej odległości od niej, więc możemy obraz
ich uzyskać na płycie fotograficznej B. Prążki interferencyjne są widoczne w postaci cienkich,
ciemnych linii, dzięki czemu możemy osiągnąć bardzo wysoką dokładność oceny ich
zniekształceń.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

18

Na rys. 11b przedstawiono przykładowy widok układu prążków. Ze względu na dużą

dokładność opisanej metody należy zwracać uwagę, ażeby nałożona warstwa odbijająca była
jednakowej grubości i żeby nie zniekształcała sprawdzanej powierzchni. Warstwy takie
możemy uzyskać drogą naparowania w aparaturze próżniowej. W celu zapewnienia
równoległości promieni pęków padających na sprawdzane płytki umieszcza się diafragmę L
w odległości 2–3 m od nich.
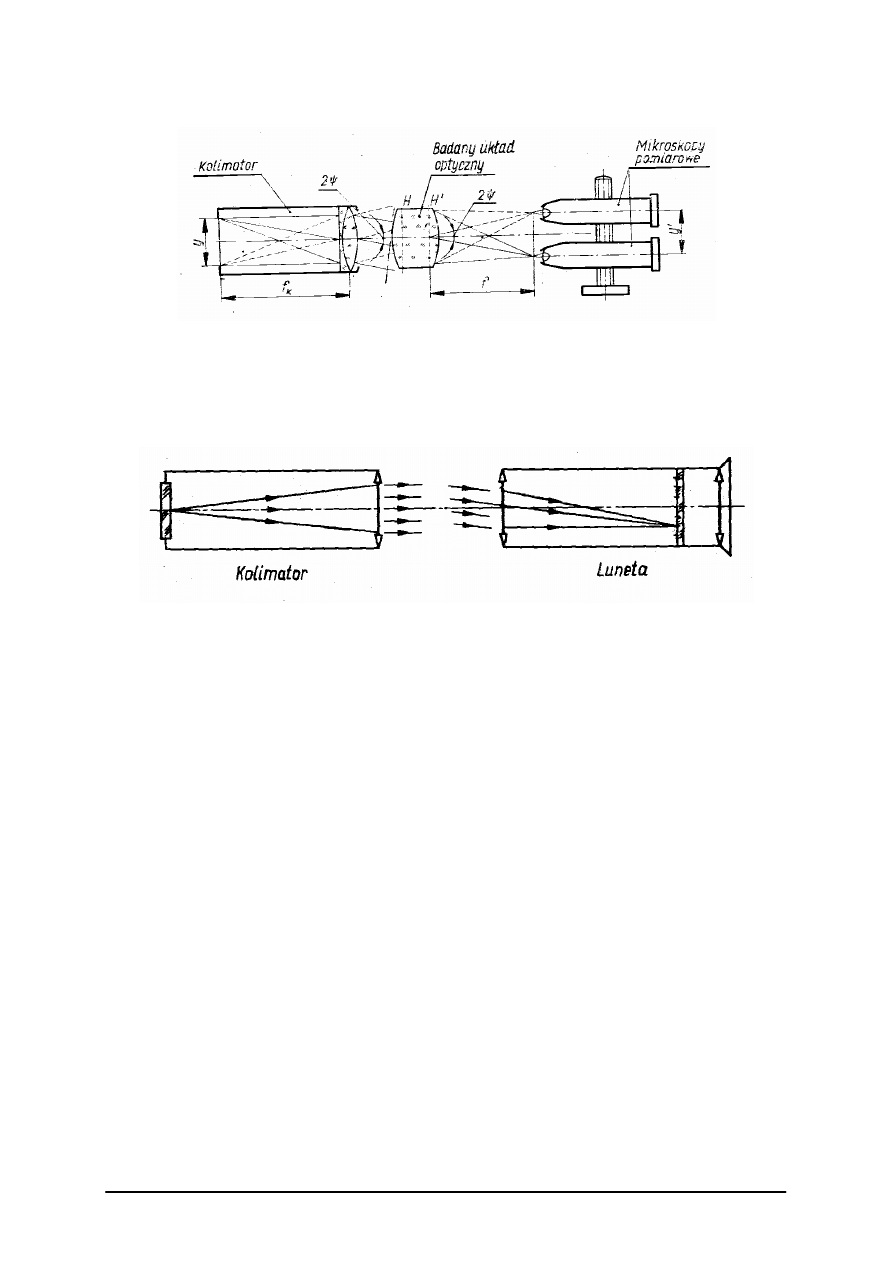
Badanie płaszczyzn za pomocą kolimatora i lunety

Bardzo często w celu określenia dokładności wykonania płaszczyzny lub całego pryzmatu

podaje się na rysunkach dopuszczalną wartość astygmatycznej różnicy pęku po odbiciu od
badanej powierzchni albo też po przejściu przez sprawdzany pryzmat lub płytkę płasko-
równoległą.

Rys. 12. Schemat układu do sprawdzania płaszczyzn [2, s. 213]

W celu pomiaru astygmatycznej różnicy powierzchni odbijającej płytki tub pryzmatu

używamy przyrządu przedstawionego schematycznie na rys. 12. Badany element optyczny
ustawiamy na stoliku S przyrządu, którego oś obrotu jest jednocześnie osią obrotu lunety L.
W płaszczyźnie ogniskowej obiektywu kolimatora K jest umieszczony test zdolności
rozdzielczej.

Luneta L przyrządu posiada przesuwny okular z krzyżem naniesionym na płytce

ogniskowej. Na oprawie okulara znajduje się podziałka, a na rurce prowadzącej lunety
noniusz, za pomocą którego mierzymy przesuw wzdłużny okulara.

Sprawdzany element optyczny (płytkę, pryzmat) orientujemy względem kolimatora

w takim położeniu, w jakim pracuje w przyrządzie. W przypadku badania płaskiej
powierzchni ustawiamy ją pod możliwie dużym kątem do osi kolimatora.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

19

Lunetę przyrządu obracamy do chwili zobaczenia obrazu testu kolimatora, utworzonego

przez badany element. Jeżeli płaszczyzna lub badany element optyczny nie jest wykonany
idealnie, to pojawi się astygmatyzm. Aby zobaczyć ostro w płaszczyźnie krzyża okulara
lunety poziome, a następnie pionowe kreski testu, należy przesunąć okular o pewną wielkość.
Wielkość tę możemy wyrazić w dioptriach okularowych lunety, pamiętając, że jednej dioptrii
odpowiada poosiowo. Powiększenie lunety powinno być odpowiednio dobrane, tak abyśmy
mogli rozpatrywać test o kącie między kreskami nie większym niż obliczony ze wzoru:

2

"'

1000

1

ok

D

f

′

⋅

=

∆

gdzie:
f´

2

ok

stanowi ogniskową okulara wyrażoną w milimetrach.

Kolimator przyrządu powinien mieć obiektyw o długości ogniskowej od 600 do 1000 mm

oraz lunetę o tej samej długości ogniskowej i otworze obiektywu.

Powiększenie lunety powinno być tak dobrane, aby spełniało warunek:

0

12

0

6

0

14

′′

÷

′′

≥

⋅

′′

G

D

k

gdzie:
D

k

– średnica czynna obiektywu kolimatora K i lunety L w milimetrach,

G – powiększenie lunety.

Doświadczony obserwator wyczuwa różnicę ustawienia krzyża okulara i obrazu testu

wynoszącą 0,1 ± 0,25 dioptrii i błąd ten przy dużym powiększeniu lunety jest bez
praktycznego znaczenia.

Sprawdzenie płaszczyzny – jakkolwiek mniej dokładne – można wykonać za pomocą

lunety autokolimacyjnej ustawionej prostopadle do badanego elementu optycznego.
W przypadku gdy badana płaszczyzna jest wykonana nieprawidłowo (powierzchnia kulista),
autokolimacyjny obraz krzyża nie będzie widziany ostro w płaszczyźnie krzyża płytki
ogniskowej lunety. Jeśli powierzchnia ma inne krzywizny w dwóch wzajemnie prostopadłych
przekrojach, to pojawi się astygmatyzm i obraz pionowego oraz poziomego ramienia krzyża
nie będzie jednakowo ostry. Przesunięcie poosiowe okulara wraz z płytką ogniskową (lub
obiektywu) konieczne do oglądania raz poziomej, drugi raz pionowej kreski auto-
kolimacyjnego obrazu krzyża lunety będzie odpowiadało astygmatycznej różnicy ∆T".

Jeśli luneta autokolimacyjna ma dwie płytki ogniskowe, to w kolimatorowej jej części

możemy wstawić test zdolności rozdzielczej, otrzymując odpowiednik kolimatora i lunety.
Metoda ta jest mniej dokładna niż omówiona poprzednio, gdyż pęki promieni wychodzące
z lunety autokolimacyjnej, padają prostopadle lub prawie prostopadle do powierzchni badanej.
Natomiast wszystkie błędy wykonania powierzchni tym bardziej się uwypuklają, im większy
jest kąt padania promieni na powierzchnię.

Pomiar promienia krzywizny

Promień krzywizny możemy zmierzyć:

1.

szklanym sprawdzianem interferencyjnym,

2.

interferometrem,

3.

bardzo duże promienie metodą interferencyjną,

4.

średniej wielkości promienie sferometrem pierścieniowym,

5.

mikroskopem autokolimacyjnym,

6.

sferometrem czujnikowym.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

20

Dwie pierwsze metody zostały dokładnie opisane w pakiecie charakteryzowanie

elementów optycznych w (731[04].Z1.01) w punkcie 4.5.

Bardzo duże promienie mierzymy metodą interferencyjną. Badaną powierzchnię

sferyczną kładziemy na sprawdzianie płaskim i mikroskopem pomiarowym mierzymy
średnicę d

N

N-tego pierścienia Newtona oraz d

M

M-tego pierścienia, a promień wyliczamy wg

wzoru

(

)

M

N

d

d

r

M

N

−

⋅

−

=

λ

4

2

2

Promienie średniej wielkości (50÷1000 mm) najczęściej używa się sferometrów

pierścieniowych.

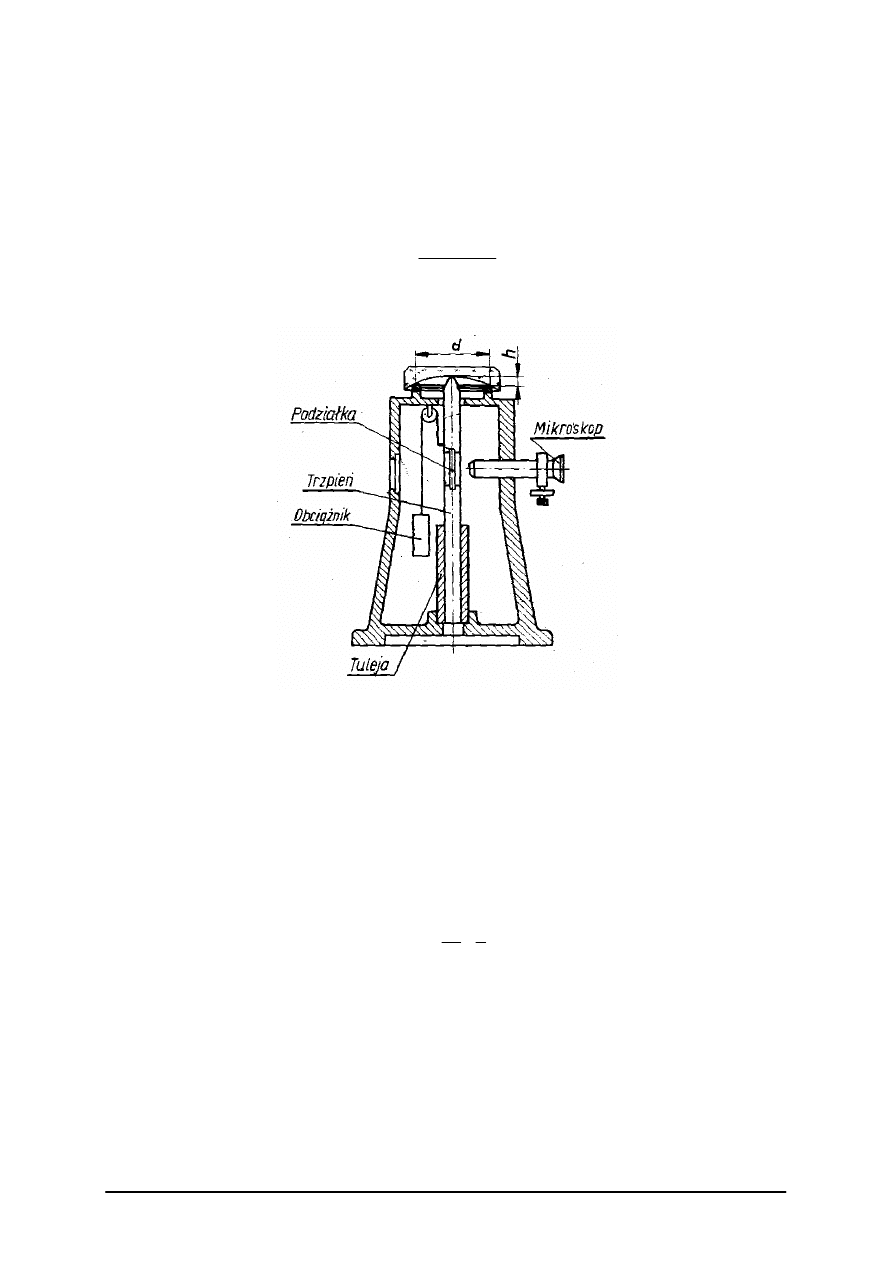
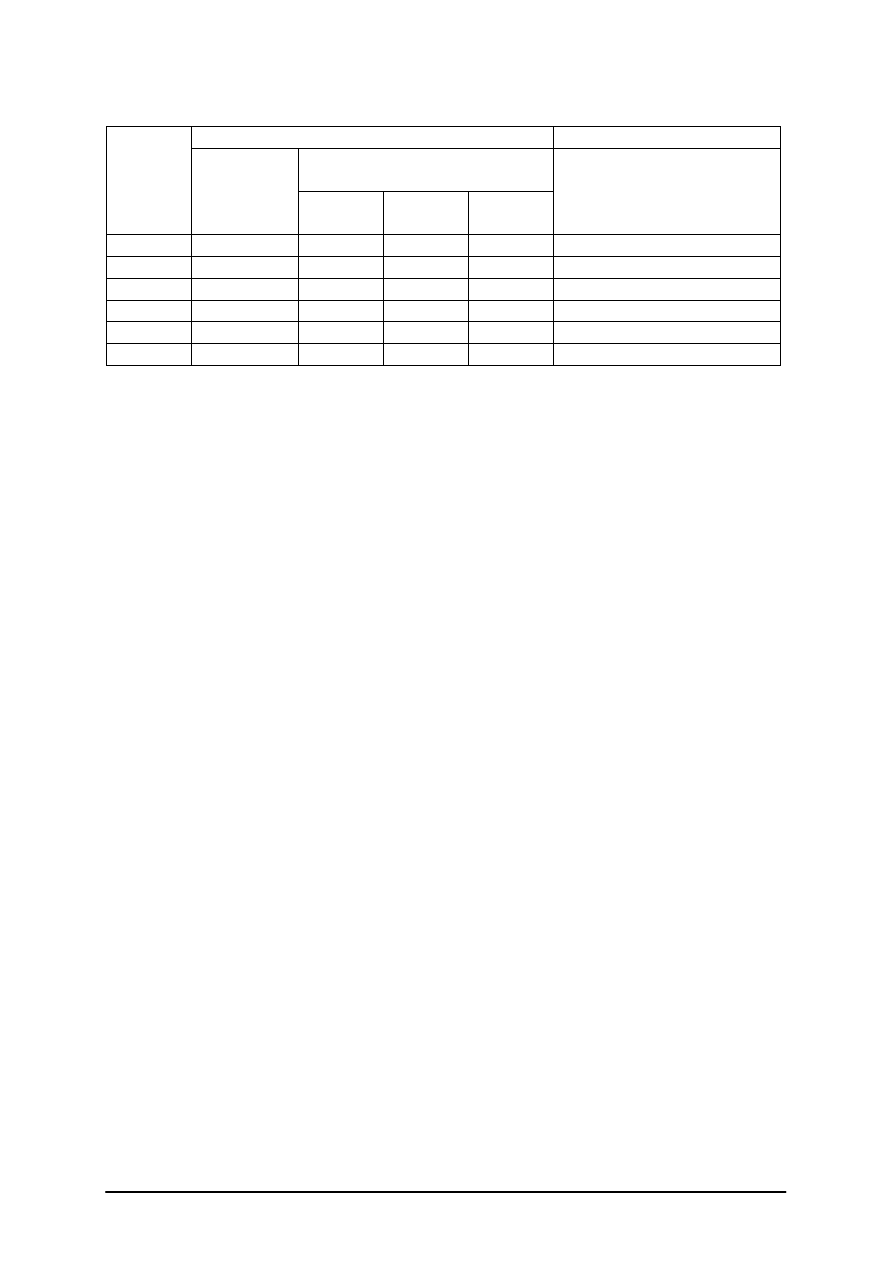
Rys. 13. Sferometr pierścieniowy [9, s. 325]

W tulei prowadzącej porusza się trzpień z kulką, który pod działaniem obciążnika

podnosi się ku górze. Na trzpieniu znajduje się podziałka, którą obserwujemy przez
mikroskop pomiarowy zapewniający dokładność odczytu do 0,001 mm. Na gniazdo osadcze
znajdujące się na górze przyrządu, współśrodkowo względem osi trzpienia, możemy nakładać
pierścienie o różnych średnicach dokładnie pomierzonych.

Pomiar polega na wyznaczeniu strzałki h czaszy kulistej poprzez odczyty położenia

trzpienia pomiarowego przy nałożonym sprawdzianie płaskim oraz po nałożeniu badanej
powierzchni. Różnica obu odczytów jest równa strzałce h badanej sfery, a szukany promień
wyznaczamy wg wzoru

2

8

2

h

h

d

r

+

=

Gdzie h – strzałka zmierzona na pierścieniu o średnicy d.

Pomiar promienia za pomocą mikroskopu autokolimacyjnego opiera się na

własnościach tego mikroskopu, który tworzy ostre obrazy autokolimacyjne, gdy
w płaszczyźnie przedmiotowej znajdzie się powierzchnia odbijająca lub jej środek krzywizny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

21

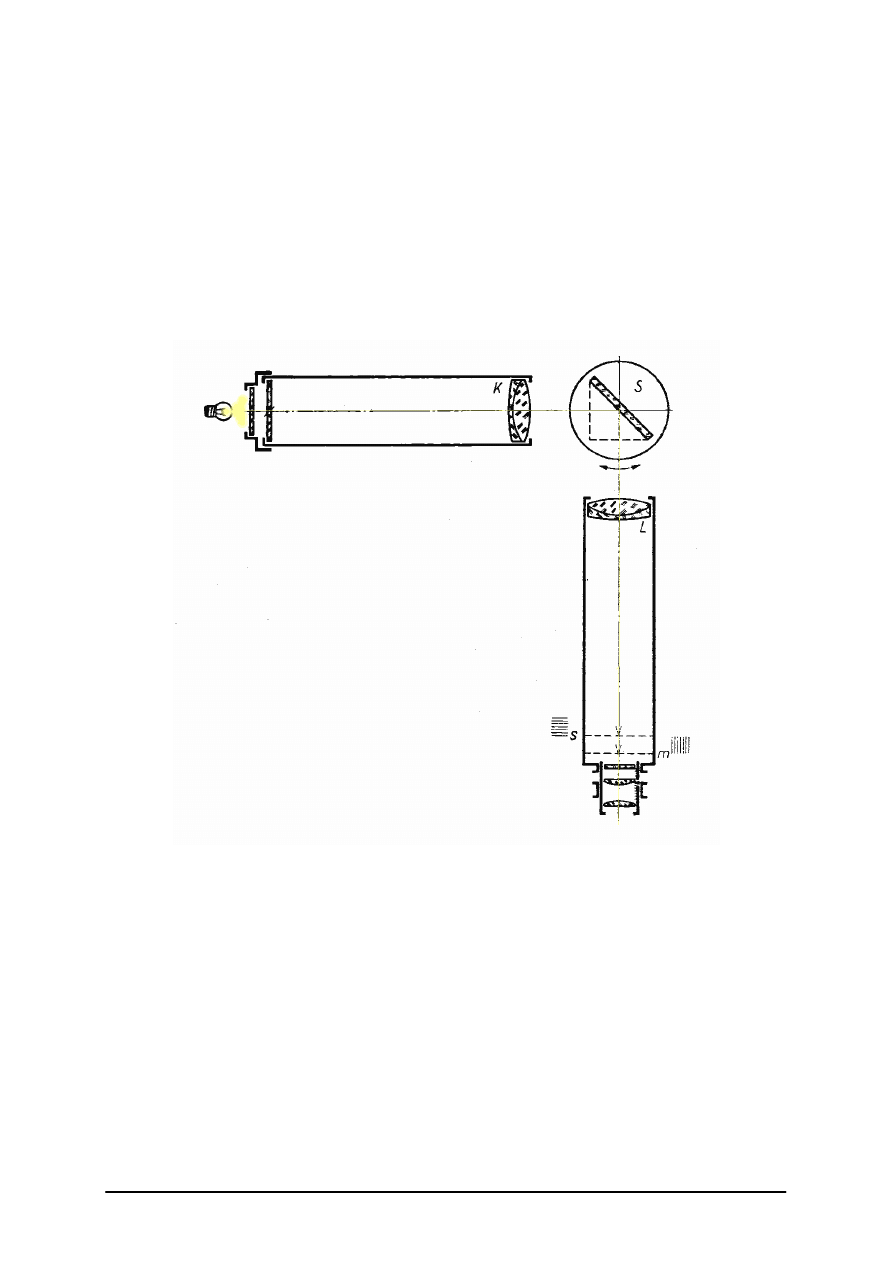
Rys. 14. Mikroskop autokolimacyjny [9, s. 270]

Wystarczy znać położenia mikroskopu lub badanej powierzchni, aby z różnicy odczytów

położeń, w których tworzą się ostre obrazy autokolimacyjne, otrzymać wartość promienia.
Takie pomiary dokonujemy na ławie optycznej osiągając dokładność pomiaru 1 µm.

Sferometr czujnikowy służy do szybkiego pomiaru promienia przeważnie szkieł

okularowych.

Rys. 15. Sferometr czujnikowy [2, s. 168]

Jest to czujnik zegarowy zaopatrzony w dwie nieruchome nóżki, których zakończenia

znajdują się na jednej linii z przesuwnym trzpieniem mierniczym, w odległości 10–15 mm.
Zerowe położenie trzpienia sprawdza się na płaskiej powierzchni. Przy pomiarze należy
zwracać uwagę, aby obie nóżki i trzpień stykały się z mierzoną powierzchnią wzdłuż okręgu
wielkiego koła. Odczyty otrzymujemy na okrągłej skali, która jest wycechowana bezpośrednio
w dioptriach.

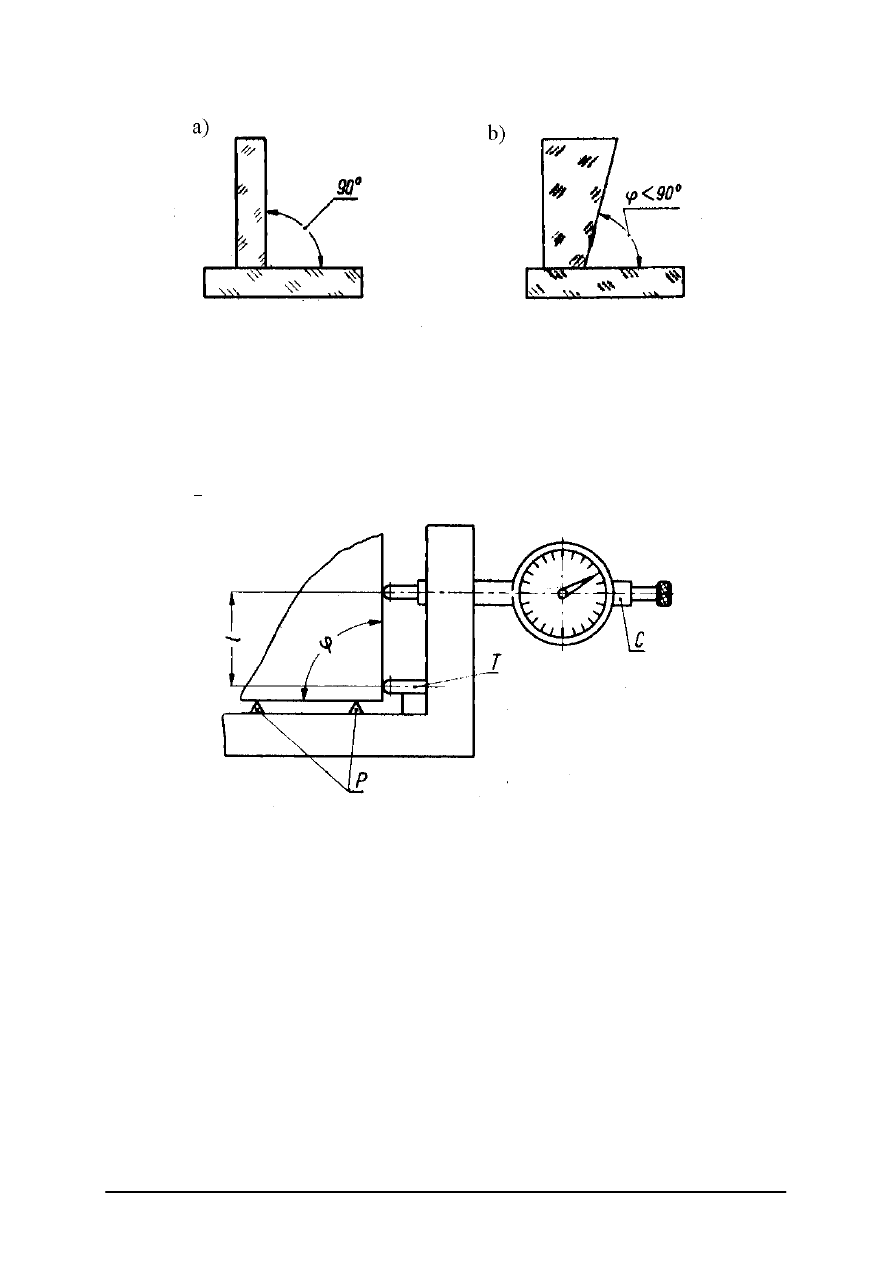
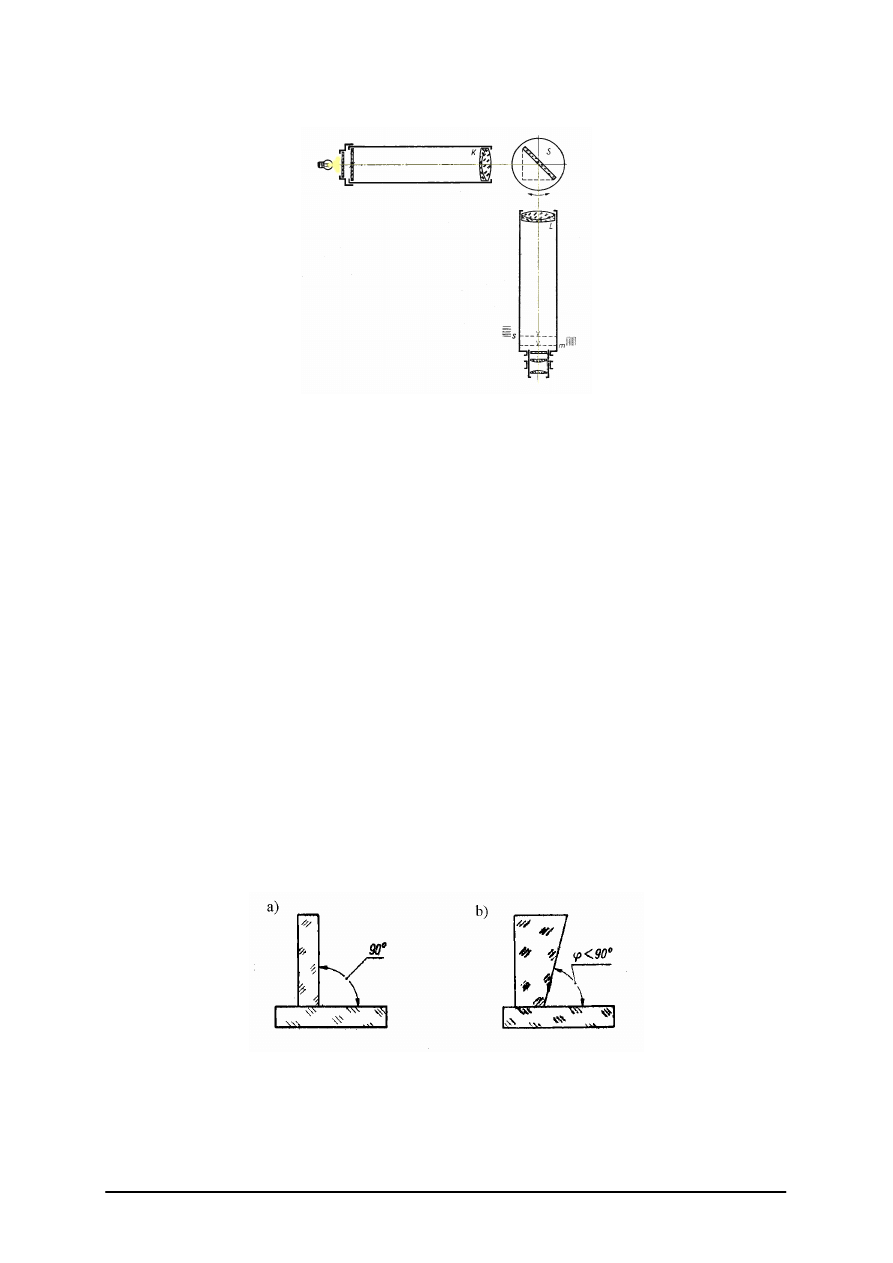
Pomiar kątów.

Jedną z najprostszych metod kontroli kątów jest sprawdzanie wg prześwitu powstającego

przy nałożeniu szklanego kątownika na ściany kąta mierzonego. Podczas sprawdzania należy
uważać, aby ramiona kątownika były prostopadłe do krawędzi sprawdzanego kąta
dwuściennego. Praktyczna dokładność pomiaru wynosi 1’÷2’.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

22

Rys. 16. Kątowniki szklane do sprawdzania pryzmatów polerowanych: a) o kącie prostym,

b) o kącie ostrym [2, s. 230]

Polerowane pryzmaty sprawdzamy szklanymi sprawdzianami interferencyjnymi

wykonanymi w postaci pryzmatu o kącie dopełniającym sprawdzany kąt do 180°. Pryzmat
taki jest przyspojony na kontakt optyczny do płaskiego sprawdzianu.

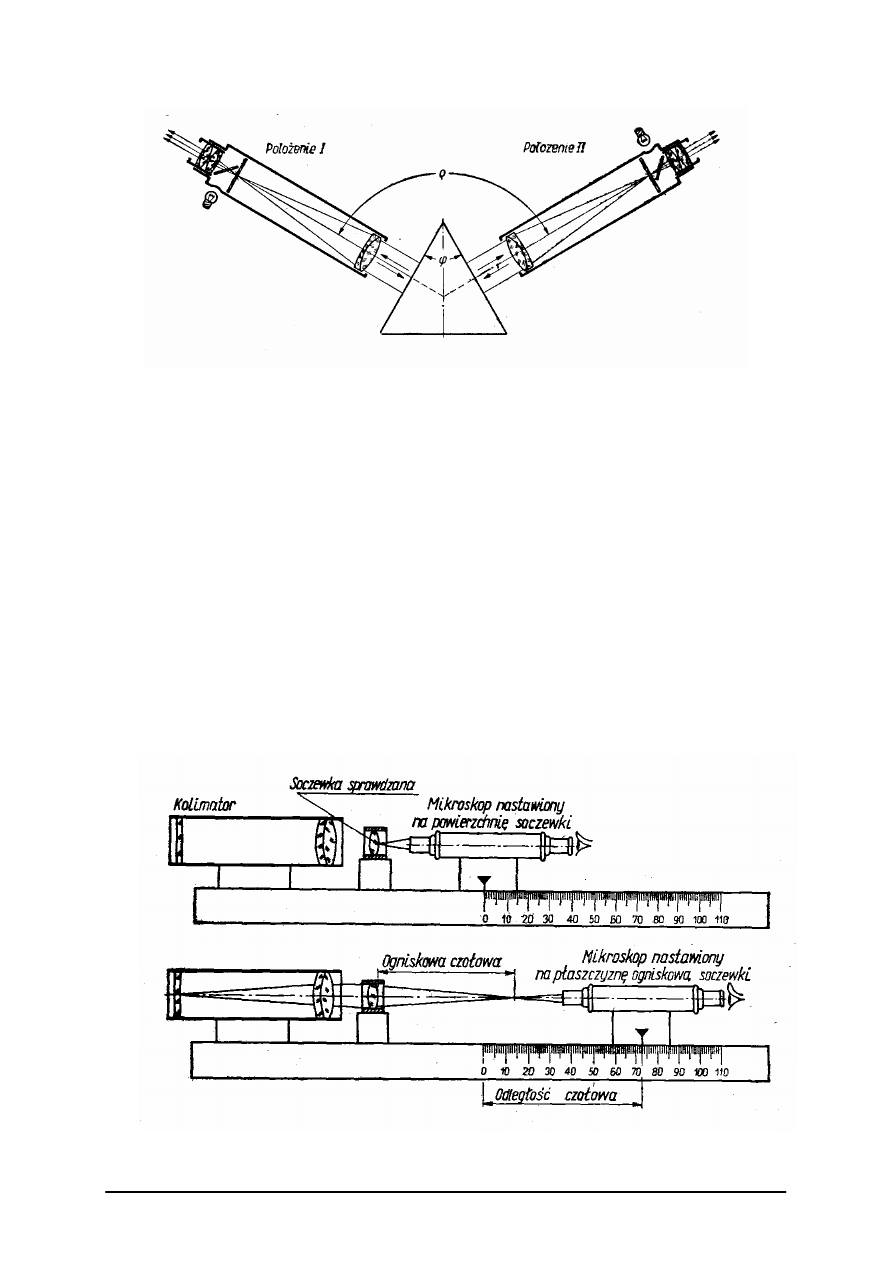
Do kontroli kątów pryzmatów używa się często czujniki oraz mechaniczne kątomierze

czujnikowe.

Rys. 17. Czujnik do sprawdzania kątów [2, s. 231]

.

Podziałka w tych czujnikach jest wyskalowana w minutach, a błąd pomiaru wynosi 1’÷2’.

Kąty dwuścienne w pryzmatach możemy również pomierzyć za pomocą goniometru.

Opis działania goniometru jest opisany w punkcie 4.1.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

23

Rys. 18. Pomiar kąta za pomocą goniometru [2, s. 233]

Sposób pomiaru kąta na goniometrze:

–

ustawiamy mierzony pryzmat na stoliku goniometru,

–

justujemy pryzmat trzema śrubami regulacyjnymi stolika do momentu, aż do momentu,
gdy utworzony przez lunetę autokolimacyjną obraz poziomej kreski krzyża pokrywa się
z poziomą kreską lunety,

–

obracamy stolik lub lunetę do chwili, gdy autokolimacyjny obraz od pierwszej ściany
pryzmatu pokryje się z krzyżem lunety,

–

następnie obracamy stolik lub lunetę do momentu pokrycia się obrazu autokolimacyjnego
od drugiej ściany pryzmatu z krzyżem lunety,

–

różnica odczytów σ na kręgu obu położeń lunety lub stolika daje nam dopełnienie kąta φ
do kąta półpełnego.

σ

ϕ

−

=

0

180

Pomiar ogniskowych

Odległość ogniskową czołową (odległość od ogniska do ostatniej powierzchni soczewki)

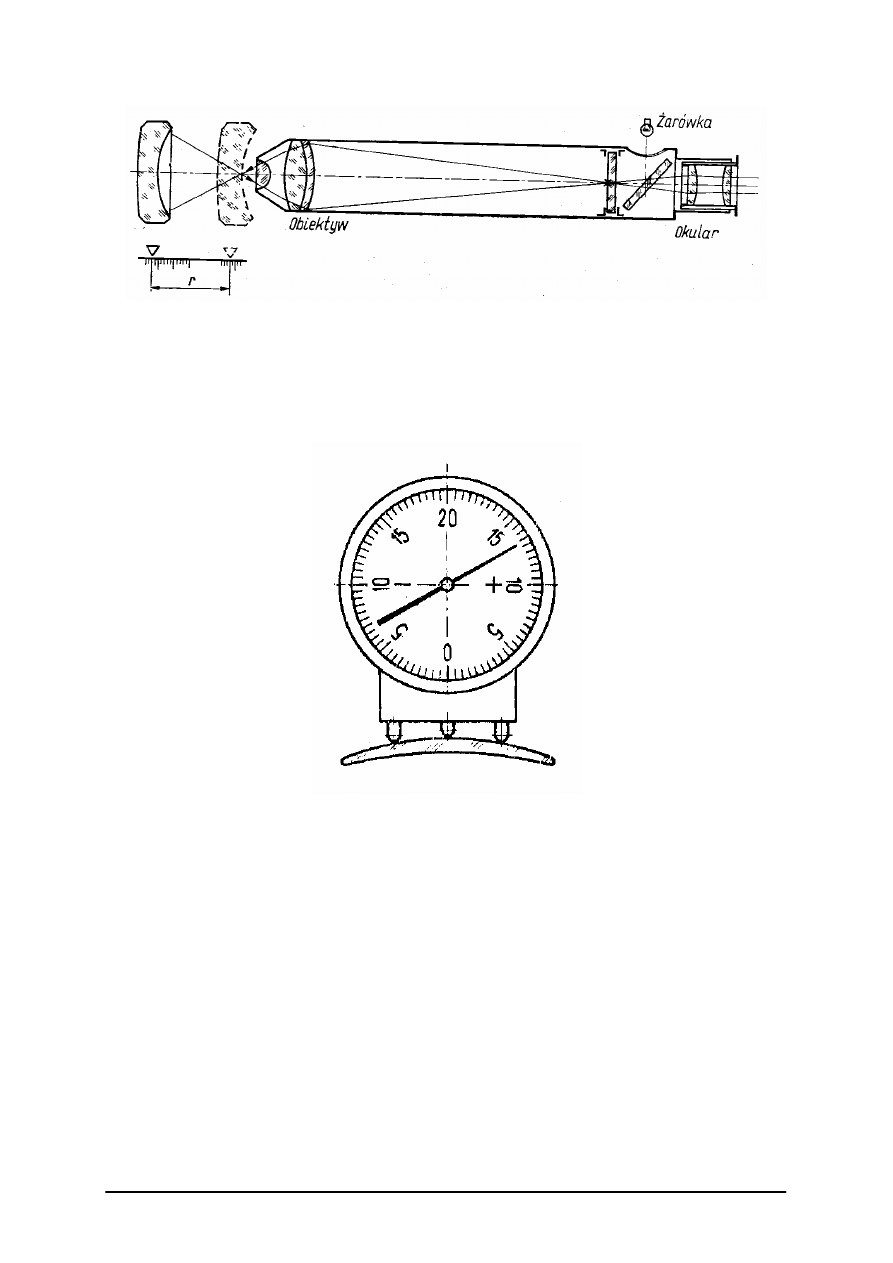
mierzymy na ławie optycznej w układzie pokazanym na rysunku nr 19.

Rys. 19. Pomiar ogniskowej czołowej [9, s. 333]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

24

Przesuwamy mikroskop do soczewki tak, aby w płaszczyźnie krzyża okulara mikroskopu

była ostro widoczna powierzchnia soczewki (np.: pyłki lub znaki wykonane miękkim
ołówkiem na tylnej powierzchni soczewki). Następnie odsuwamy mikroskop aż do uzyskania
w płaszczyźnie krzyża okulara ostrego obrazu krzyża kolimatora. Długość przesunięcia
mikroskopu mierzona na podziałce ławy, jest odległością ogniskową czołową s

F

’.

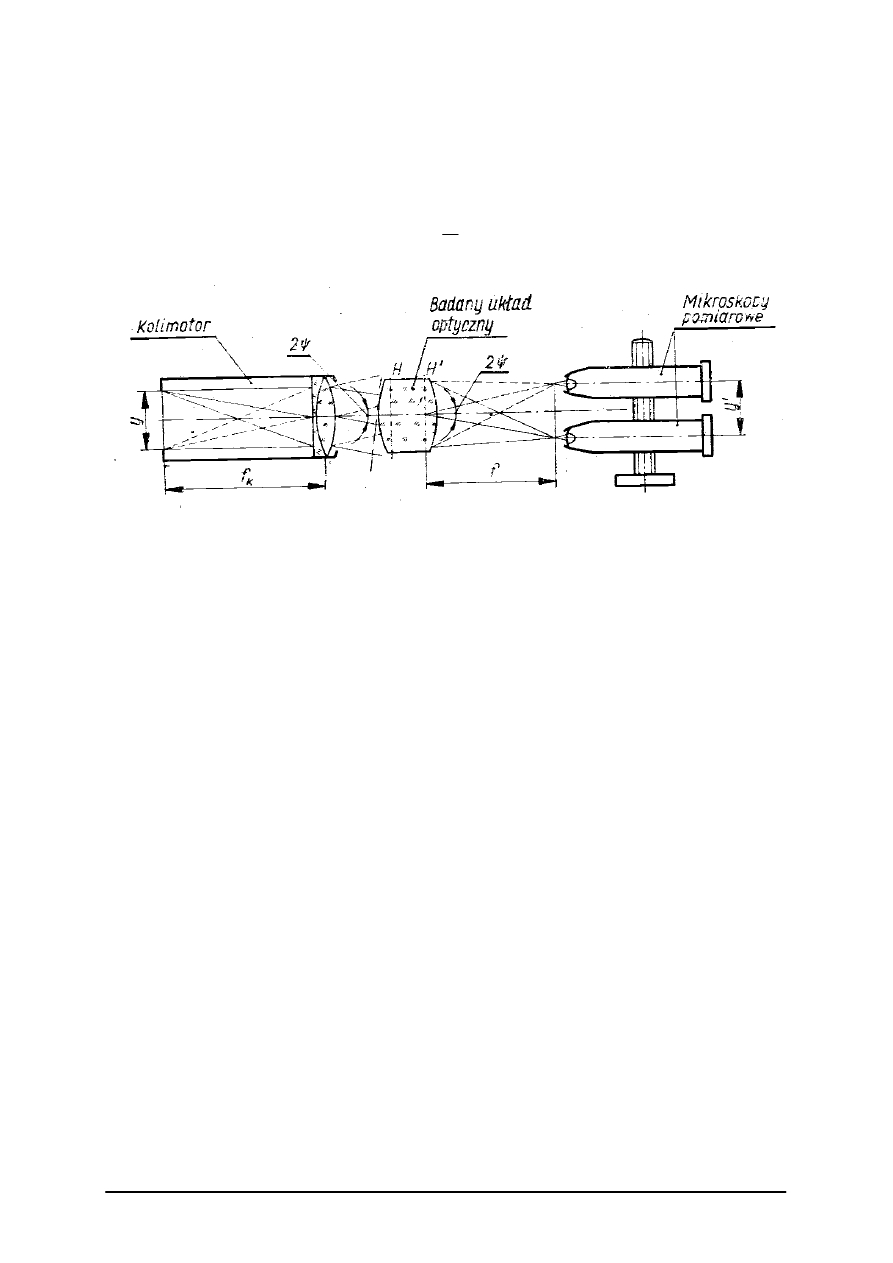
Ogniskową a tym samym moc soczewki

f

′

=

1

ϕ

układu optycznego lub soczewki mierzymy

w układzie kolimator, badana soczewka, mikroskop pomiarowy jak na rysunku nr 20.

Rys. 20. Pomiar ogniskowych [9, s. 334]

Pomiar polega na wyznaczeniu odległości y’ obrazów kresek kolimatora. Pomiaru

możemy dokonać naprowadzając kolejno obrazy kresek kolimatora na środek krzyża
mikroskopu pomiarowego poprzez poprzeczny przesuw mikroskopu lub badanego układu
optycznego. Odległości mierzymy za pomocą urządzenia odczytowego z dokładnością
±0,002 mm.

Ogniskową wyznaczamy ze wzoru

y

k

f

′

⋅

=

gdzie:
f – ogniskowa badanego układu,
k – stała kolimatora,
y’ – odległość obrazów kresek kolimatora utworzonych przez badany układ.

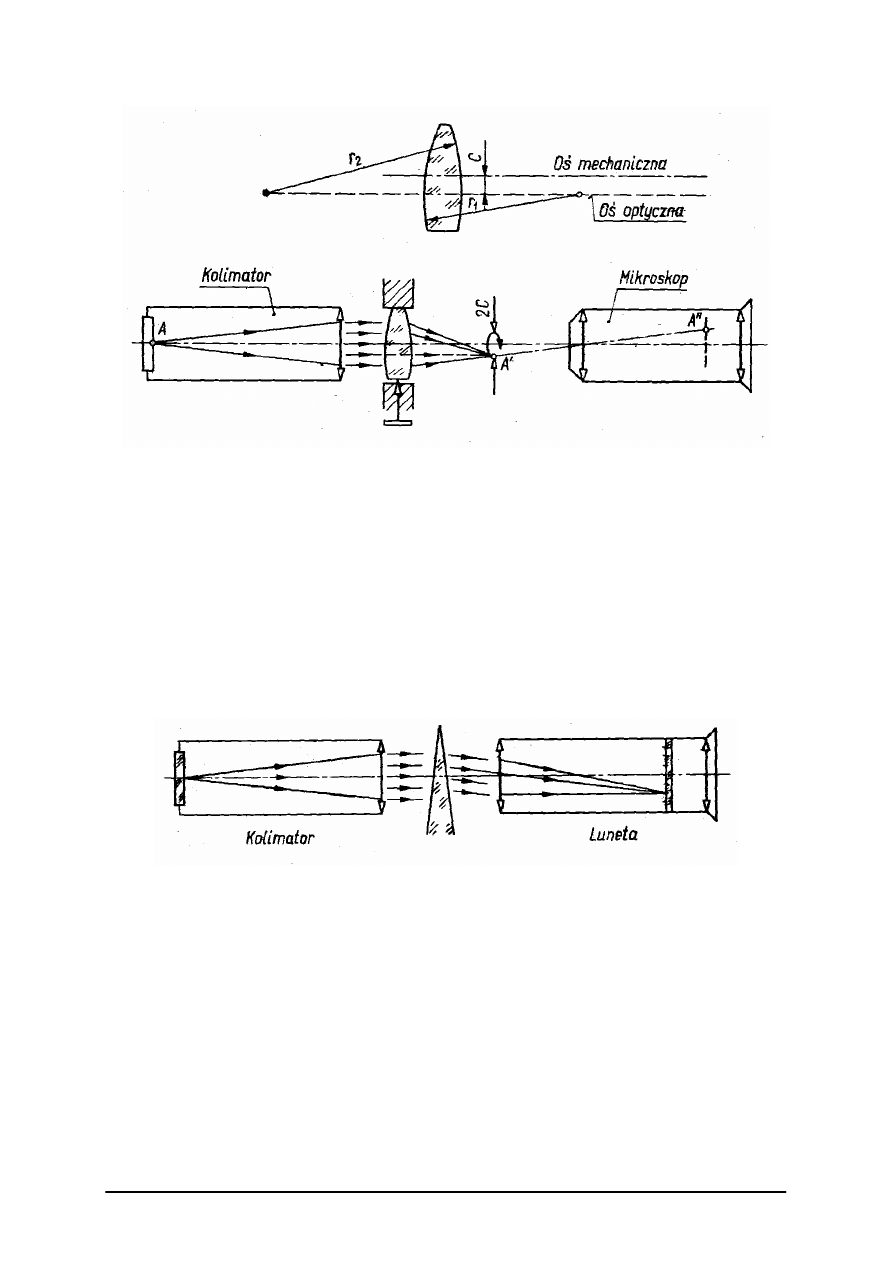
Sprawdzenie centralności soczewek i klinowatości płytek

W prawidłowo wykonanej soczewce oś optyczna powinna pokrywać się z osią

mechaniczną; w przeciwnym razie występuje błąd zwany niecentrycznością soczewki.

Niecentryczność (niecentralność, nieśrodkowość) mierzymy w świetle przechodzącym

(można również mierzyć w świetle odbitym) w układzie kolimator, mierzona soczewka,
mikroskop jak na rysunku 21.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

25

Rys. 21. Pomiar centralności soczewek [9, s. 337]

Przy obrocie badanej soczewki wokół jej osi mechanicznej obraz krzyża kolimatora,

utworzony w ognisku obrazowym tej soczewki, zatacza koło o promieniu, który jest miarą
niecentryczności.

Klinowatość płytek (kat łamiący θ klina) najczęściej sprawdzamy za pomocą lunety

autokolimacyjnej. Zasada pomiaru omówiona jest w pakiecie modułu Z1.02. w punkcie 4.4.
Znając kąt łamiący klina można obliczyć kat odchylenia δ ze wzoru

( )

θ

δ

⋅

−

=

1

n

. Warunkiem

stosowania tej metody jest znajomość współczynnika załamania n szkła z jakiego wykonany
jest klin.

Bezpośrednio kąt odchylenia klina wyznaczamy w układzie kolimator – luneta

z podziałką kątową rysunek 22.

Rys. 22. Pomiar kata odchylenia klina [9, s. 337]

Na początku pomiaru ustawiamy lunetę tak, aby obraz krzyża kolimatora pokrył się

z zerową kreską podziałki kątowej lunety. Wstawiamy badany kliniak na rysunku 22. Teraz
obraz krzyża przesunie się w polu widzenia lunety o wartość kątową odpowiadającą kątowi
odchylenia klina.

Sprawdzanie wymiarów liniowych i kątowych
–

Wymiary liniowe jak grubość i średnica soczewki, boki pryzmatów mierzymy
uniwersalnymi narzędziami do pomiaru długości jak: suwmiarka, mikrometr, czujnik,
mikroskopy pomiarowe.

–

Fazy na elementach optycznych mierzymy za pomocą lup pomiarowych.

–

Bezwzględne pomiary kątów mierzymy za pomocą goniometrów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

26

–

W praktyce warsztatowej kąty najczęściej mierzymy metodami porównawczymi
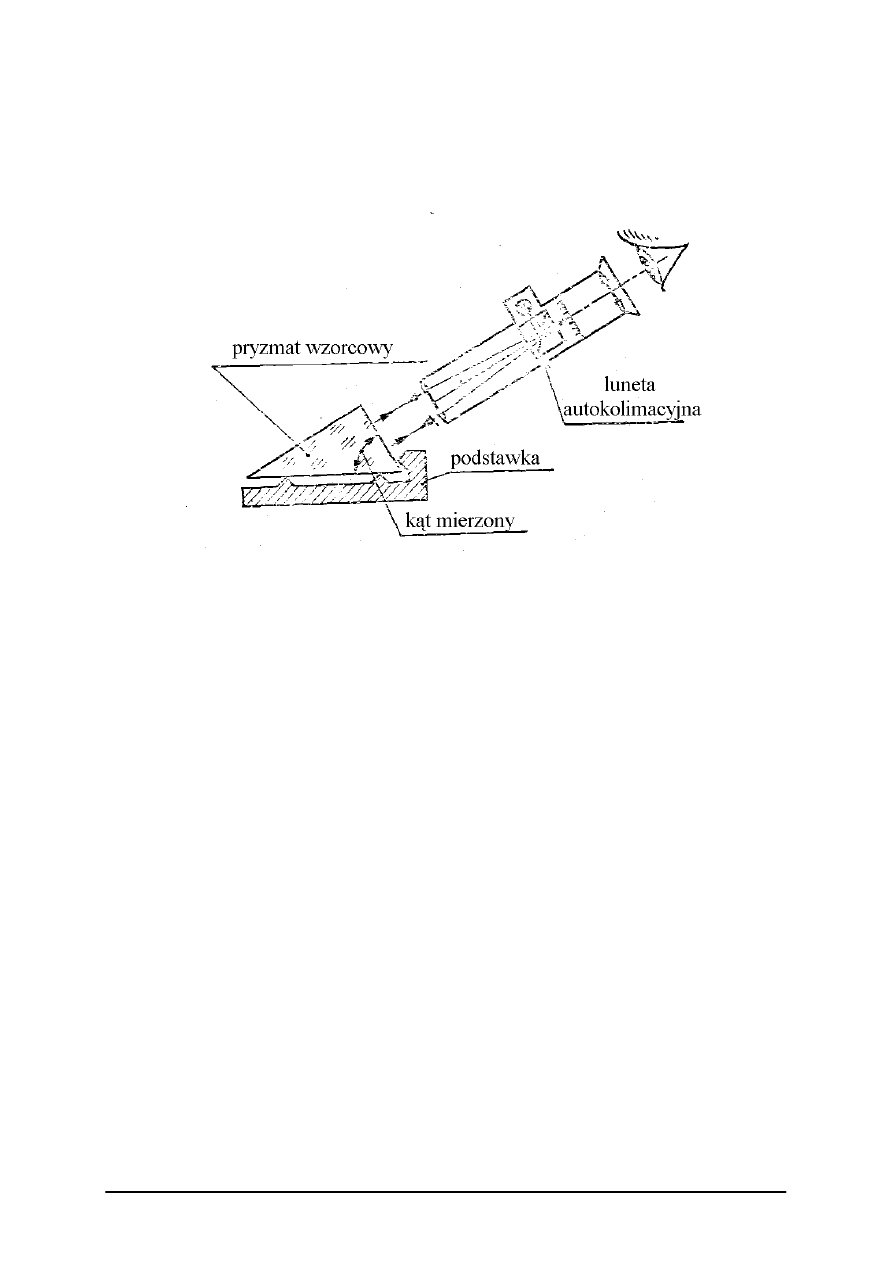
z wykorzystaniem lunet autokolimacyjnych. W metodzie tej najpierw wykonuje się
pryzmat wzorcowy mierzony za pomocą goniometru. Za pomocą pryzmatu wzorcowego
ustawiamy lunetę autokolimacyjną na zero jak na rysunku 23. Za pomocą lunety
autokolimacyjnej mierzymy odchyłki kątowe względem pryzmatu wzorcowego.

Rys. 23. Pomiar odchyłek kątowych z użyciem lunety autokolimacyjnej

[9, s. 338]

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

W jaki sposób można dokonać sprawdzenia powierzchni płaskich?

2.

W jaki sposób można dokonać pomiaru promienia krzywizny?

3.

W jaki sposób można pomierzyć ogniskową?

4.

Jak możemy sprawdzić centralność soczewki?

5.

Jak możemy sprawdzić klinowatość płytek?

6.

Jakimi przyrządami możemy pomierzyć wymiary liniowe elementów optycznych?

7.

W jaki sposób możemy dokonać pomiarów kątów w pryzmatach?

8.

Jak zbudowany jest przyrząd do pomiaru odchyłek kątowych w pryzmatach?

4.2.3. Ćwiczenia

Ćwiczenie 1

Oblicz promień krzywizny mierzony na sferometrze wiedząc, że strzałka powierzchni

sferycznej wynosi 0,5 mm na średnicy pierścienia 35 mm.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru promienia za
pomocą sferometru,

2)

odszukać wzór na obliczanie promienia,

3)

obliczyć promień krzywizny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

27

Wyposażenie stanowiska pracy:

−

kalkulator.

Ćwiczenie 2

Wyznacz promień soczewki dodatniej, ujemnej i zwierciadła wklęsłego za pomocą

sferometru.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru promienia za
pomocą sferometru,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy sferometru,

3)

dobrać pierścienie pomiarowe do średnicy soczewek i zwierciadła,

4)

umieścić płytkę wzorcową na pierścieniu pomiarowym,

5)

dokonać zerowego odczytu położenia trzpienia pomiarowego,

6)

umieścić mierzony element na pierścieniu pomiarowym i dokonać odczytu położenia
trzpienia pomiarowego,

7)

wyznaczyć strzałkę ugięcia,

8)

wyliczyć promień krzywizny badanych elementów.

Wyposażenie stanowiska pracy:

−

sferometr,

−

instrukcja obsługi sferometru,

−

komplet pierścieni pomiarowych,

−

płytka wzorcowa,

−

soczewka dodatnia, ujemna i zwierciadło wklęsłe do pomiaru.

Ćwiczenie 3

Wyznacz promień zwierciadła wklęsłego za pomocą mikroskopu autokolimacyjnego na

ławie optycznej.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru promienia za
pomocą mikroskopu autokolimacyjnego,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy mikroskopu
autokolimacyjnego,

3)

zapoznać się z budową ławy optycznej,

4)

umieścić zwierciadło na ławie optycznej przed mikroskopem autokolimacyjnym,

5)

odszukać takie położenie mikroskopu, w którym uzyskamy ostry obraz autokolimacyjny
krzyża gdy powierzchnia odbijająca leży w płaszczyźnie przedmiotowej mikroskopu,

6)

dokonać odczytu na ławie optycznej położenia mikroskopu,

7)

odszukać takie położenie mikroskopu, w którym uzyskamy ostry obraz autokolimacyjny
krzyża gdy środek krzywizny powierzchni odbijającej leży w płaszczyźnie,
przedmiotowej mikroskopu,

8)

dokonać odczytu na ławie optycznej położenia mikroskopu,

9)

wyliczyć promień krzywizny badanych elementów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

28

Wyposażenie stanowiska pracy:

−

ława optyczna,

−

mikroskop autokolimacyjny,

−

instrukcja obsługi ławy optycznej i mikroskopu autokolimacyjnego,

−

zwierciadło wklęsłe do pomiaru.

Ćwiczenie 4

Wyznacz ogniskową czołową soczewki dodatniej na ławie optycznej.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru ogniskowych
czołowych,

2)

zapoznać się z budową ławy optycznej,

3)

zapoznać się z budową kolimatora,

4)

umieścić soczewkę mierzoną na ławie optycznej pomiędzy kolimatorem i mikroskopem,

5)

odszukać takie położenie mikroskopu, w którym uzyskamy ostry obraz powierzchni
soczewki mierzonej,

6)

dokonać odczytu na ławie optycznej położenia mikroskopu,

7)

odszukać takie położenie mikroskopu, w którym uzyskamy ostry obraz w płaszczyźnie
krzyża okulara ostrego obrazu krzyża kolimatora,

8)

dokonać odczytu na ławie optycznej położenia mikroskopu,

9)

wyliczyć ogniskową badanej soczewki.

Wyposażenie stanowiska pracy:

−

ława optyczna,

−

mikroskop,

−

kolimator,

−

instrukcja obsługi ławy optycznej i mikroskopu,

−

soczewka dodatnia do pomiaru,

Ćwiczenie 5

Wyznacz kąt łamiący w pryzmacie załamującym.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru kątów
w pryzmatach,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy i zasady działania
goniometru,

3)

zapoznać się z budową goniometru,

4)

umieścić mierzony pryzmat na stoliku goniometru pomiędzy kolimatorem i lunetą
autokolimacyjną,

5)

wyjustować pryzmat śrubami regulacyjnymi stolika,

6)

unieruchamiamy stolik,

7)

odszukać takie położenie lunety autokolimacyjnej, w którym autokolimacyjny obraz od
pierwszej ściany pryzmatu pokryje się z krzyżem lunety,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

29

8)

dokonać odczytu położenia lunety,

9)

obrócić lunetę autokolimacyjną do drugiej powierzchni pryzmatu,

10)

odszukać takie położenie lunety autokolimacyjnej, w którym autokolimacyjny obraz od
drugiej ściany pryzmatu pokryje się z krzyżem lunety,

11)

dokonać odczytu położenia lunety,

12)

wyliczyć kat łamiący pryzmatu.

Wyposażenie stanowiska pracy:

−

goniometr,

−

instrukcja obsługi goniometru,

−

pryzmat załamujący.

Ćwiczenie 6

Dokonaj pomiaru średnicy, grubości i faz w soczewce dodatniej i ujemnej.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru wymiarów
liniowych,

2)

dobrać po dwa przyrządy pomiarowe do każdego pomiaru,

3)

dokonać pomiaru średnicy soczewek,

4)

dokonać pomiaru grubości soczewek,

5)

dokonać pomiaru faz w soczewkach.

Wyposażenie stanowiska pracy:

−

uniwersalne przyrządy pomiarowe do pomiaru wymiarów zewnętrznych,

−

lupy pomiarowe,

−

soczewka dodatnia i ujemna.

Ćwiczenie 7

Dokonaj pomiaru klinowatości płytki ogniskowej.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące pomiaru płaskości
i klinowatości płytek,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące płytek płaskorównoległych
i klinów optycznych,

3)

wyszukać w materiałach dydaktycznych informacje dotyczące lunet pomiarowych
i kolimatorów,

4)

ustawić lunetę na zerową kreskę podziałki kątowej lunety,

5)

umieścić mierzoną płytkę ogniskową na ławie optycznej pomiędzy kolimatorem i lunetą,

6)

dokonać odczytu wartości kąta odchylenia płytki,

7)

wyliczyć kąt łamiący badanej płytki.

Wyposażenie stanowiska pracy:

−

ława optyczna,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

30

−

luneta autokolimacyjna,

−

kolimator,

−

instrukcja obsługi ławy optycznej i lunety,

−

płytka ogniskowa do pomiaru.

Ćwiczenie 8

Sprawdź jakość powierzchni płytki płaskorównoległej za pomocą szklanego sprawdzianu

interferencyjnego.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące interferencji, prążków
Newtona i szklanych sprawdzianów interferencyjnych,

2)

umyć dokładnie sprawdzane elementy,

3)

nałożyć sprawdzian interferencyjny na badany element,

4)

sprawdzić wygląd prążków interferencyjnych,

5)

określić N i ∆N dla badanych elementów,

6)

sporządź notatkę z wykonanego zadania.

Wyposażenie stanowiska pracy:

−

szklane sprawdziany interferencyjne płaskie,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

−

pędzelki do odpylenia,

−

lampa sodowa,

−

płytki płaskorównoległe,

−

arkusz spostrzeżeń.

Ćwiczenie 9

Sprawdź jakość powierzchni soczewki ujemnej za pomocą szklanego sprawdzianu

interferencyjnego.

Sposób wykonania ćwiczenia:

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące interferencji, prążków
Newtona i szklanych sprawdzianów interferencyjnych,

2)

umyć dokładnie sprawdzane elementy,

3)

nałożyć sprawdzian interferencyjny na badany element,

4)

sprawdzić wygląd prążków interferencyjnych,

5)

określić N i ∆N dla badanych elementów,

6)

sporządź notatkę z wykonanego zadania.

Wyposażenie stanowiska pracy:

−

szklane sprawdziany interferencyjne sferyczne wypukłe,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

31

−

pędzelki do odpylenia,

−

lampa sodowa,

−

płytki soczewki wklęsłe do pomiaru.

−

arkusz spostrzeżeń.

Ćwiczenie 10

Sprawdź jakość powierzchni otrzymanych płytek płaskorównoległych za pomocą

interferometru warsztatowego.

Sposób wykonania ćwiczenia:

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące interferencji, prążków
Newtona i interferometrów,

2)

umyć dokładnie sprawdzane elementy,

3)

zapoznać się z obsługą interferometru,

4)

ustawić interferometr do pomiaru za pomocą płytki wzorcowej,

5)

wstaw płytki do pomiaru,

6)

sprawdzić wygląd prążków interferencyjnych,

7)

określić N i ∆N dla badanych elementów,

8)

sporządź notatkę z wykonanego zadania.

Wyposażenie stanowiska pracy:

−

interferometr warsztatowy,

−

płytka wzorcowa,

−

instrukcja obsługi interferometru,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

−

pędzelki do odpylenia,

−

płytki płaskorównoległe do kontroli,

−

arkusz spostrzeżeń.

Ćwiczenie 11

Sprawdź jakość powierzchni otrzymanych płytek płaskorównoległych za pomocą

kolimatora i lunety.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące interferencji, prążków
Newtona i interferometrów,

2)

wyszukać w materiałach dydaktycznych informacje dotyczące budowy kolimatorów
i lunet pomiarowych,

3)

odczytać schemat układ pomiarowego,

4)

dobrać i przygotować przyrządy kontrolne do pomiaru,

5)

zestawić układ pomiarowy,

6)

umyć dokładnie sprawdzane elementy,

7)

wstaw płytki do pomiaru,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

32

8)

dokonaj badania płaskości otrzymanych płytek,

9)

sporządź notatkę z wykonanego zadania.

Wyposażenie stanowiska pracy:

−

kolimator,

−

luneta pomiarowa,

−

ława optyczna,

−

schemat układu pomiarowego,

−

instrukcja wykonania badania powierzchni płytek,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

−

pędzelki do odpylenia,

−

płytki płaskorównoległe do kontroli,

−

arkusz spostrzeżeń.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

omówić budowę goniometru?

2)

określić zastosowanie ławy optycznej?

3)

określić zastosowanie szklanych sprawdzianów interferencyjnych?

4)

rozróżnić

przyrządy

pomiarowe

do

pomiarów

parametrów

geometrycznych elementów optycznych?

5)

scharakteryzować

zastosowanie

lunety

autokolimacyjnej

do

pomiarów parametrów elementów optycznych?

6)

scharakteryzować

zastosowanie

kolimatorów

do

pomiarów

parametrów elementów optycznych?

7)

scharakteryzować zastosowanie mikroskopów pomiarowych do
pomiarów parametrów elementów optycznych?

8)

dokonać pomiaru kąta?

9)

dokonać pomiaru promienia?

10)

sprawdzić powierzchnię płaską?

11)

dokonać pomiaru ogniskowych?

12)

sprawdzić klinowość płytki?

13)

dokonać pomiarów liniowych elementów optycznych?

14)

obsłużyć interferometr warsztatowy?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

33

4.3. Czystość optyczna

4.3.1. Materiał nauczania

Czystość powierzchni elementów optycznych charakteryzuje się ilością i rozmiarami skaz

występujących na tej powierzchni. Jako skazy uważa się rysy i punkty (przeszlifowane
pęcherze, wykłucia, plamki, szczerby, nadtrawienia i inne mające charakter punków). Dotyczy
ona tylko obszarów czynnych – tej części powierzchni przez którą przechodzą lub się odbijają
promienie świetlne.

Jeśli:

–

obszar czynny jest kołem – to jego średnicę nazywamy średnicą czynną,

–

obszar czynny nie jest kołem, to jako średnicę czynną rozumie się średnicę koła
wpisanego w ten obszar.

Obszar czynny dzielimy na strefy:

–

centralną – powierzchnia ograniczona okręgiem o średnicy nie większej niż 1/3 średnicy
czynnej,

–

środkową – powierzchnia ograniczona okręgiem o średnicy nie większej niż 2/3 średnicy
czynnej,

–

brzegową – pozostała część obszaru czynnego.
W zależności od liczby i rozmiarów wad występujących na powierzchni czynnej polska

norma określa klasy czystości i metody ich sprawdzania.
Fragmenty normy dotyczącej klas czystości

Przy badaniu elementów I klasy czystości do oględzin należy używać lupy

o powiększeniu, pod jakim element pracuje, lecz nie mniejszym niż 6

x

.

Przy badaniu elementów w klasie PI-0S przeglądanie powinno odbywać się przy użyciu

mikroskopu o powiększeniu ≥10

x

, w ciemnym polu, w świetle odbitym pod katem 45°.

Przy badaniu elementów w klasach PI-10S do PI-40S przeglądanie powinno odbywać się

przy użyciu mikroskopu o powiększeniu ≤ 10

x

.

Tabela 1. Dopuszczalne skazy powierzchni w klasie I [opracowanie własne]

Strefa środkowa

Strefa brzegowa

Strefa centralna

punkty

rysy

Punkty

rysy

liczba

liczba

K

la

sy

c

zy

st

o

śc

i

Ś

re

d

n

ic

a

w

m

m

D

o

4

0

P

o

n

ad

4

0

S

ze

ro

k

o

ść

w

m

m

Ł

ąc

zn

a

d

łu

g

o

ść

w

m

m

Ś

re

d

n

ic

a

w

m

m

D

o

4

0

P

o

n

ad

4

0

S

ze

ro

k

o

ść

w

m

m

Ł

ąc

zn

a

d

łu

g

o

ść

w

m

m

Zagęszczenie wad

PI-0 Wymiary wad, ich liczbę w strefach i wymiary stref ustala się na

rysunku części

PI-
10

0,004

4

6

0,002

0,2D 0,006

8 12

0,002

0,4D

PI-
20

0,010

4

6

0,004

0,2D 0,015

8 12

0,004

0,4D

PI-
40

0,015

4

6

0,008

0,2D 0,025

8 12

0,008

0,4D

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

34

PI-
0S

Wymiary wad, ich liczbę w strefach i wymiary stref ustala się na
rysunku części

Niedopuszczalne
są defekty
widoczne
w warunkach
kontroli

PI-
10S

0,004

4

6

0,002

0,2D 0,006

8 12

0,002

0,4D

PI-
20S

0,010

4

6

0,004

0,2D 0,015

8 12

0,004

0,4D

PI-
40S

0,015

4

6

0,008

0,2D 0,025

8 12

0,008

0,4D

Nie więcej niż 1
punkt oraz mniej
niż 10 rys o łącznej
długości mniejszej
od 0,1 D; pozostałe
wymagania określa
konstruktor na
rysunku
technicznym

KLASY CZYSTOŚCI P II - P VII

Punkty powstają w skutek przeszlifowania pęcherzy powietrznych znajdujących się

w szkle lub są pozostałością głębokich kraterów utworzonych na powierzchni szkła przez
pojedyncze grube ziarna proszku ściernego.

Rysy mogą być pozostałościami po poprzednim szlifowaniu lub też uszkodzeniami

powierzchni powstałymi w czasie polerowania, wskutek zanieczyszczenia proszku do
polerowania, użycia zbyt twardej smoły, niedostatecznej wilgotności polerowanej
powierzchni.

Dla klasy P II skazy wykrywa się w świetle odbitym na tle czarnego ekranu (żarówka

o mocy 40–60 W).

Dla klasy P III – P VIII skazy wykrywa się w świetle przechodzącym na tle równomiernie

oświetlonej matówki (żarówka o mocy 40–60 W osłonięta matową szybą. Odległość szyby od
włókna żarówki wynosi 100 mm, a od matówki do sprawdzanego materiału ok. 150 mm).

Tabela 2. Dopuszczalne skazy powierzchni w klasach II–VII [opracowanie własne]

punkty

duże punkty

łączna liczba w zależności od średnicy
czynnej D w mm

Klasa
czystości średnica

w mm

do 15

16–25

pow. 25

ilość
maks. 25% liczby punktów
o średnicy większej
niż

P II

0,002–0,06

0,5 D

0,75 D

1,0 D

P III

0,004–0,1

0,8 D

1,2 D

1,6 D

0,06 mm

P IV

0,015–0,3

0,8 D

1,2 D

1,6 D

0,1 mm

P V

0,015–0,6

1,0 D

1,5 D

2,0 D

0,3 mm

P VI

0,015–1,0

1,0 D

1,5 D

2,0 D

0,6 mm

P VII

0,3–2,0

1,0 D

1,5 D

2,0 D

1,0 mm

Punktów o średnicy mniejszej niż podana w tabelce nie bierze się pod uwagę, jeżeli nie

mają charakteru skupisk (niedopolerowania).

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

35

Tabela 3. Dopuszczalne skazy (rysy) powierzchni w klasie II–VII [opracowanie własne]

rysy

duże rysy

łączna długość zależności od
średnicy czynnej D w mm

Klasa
czystości szerokość

w mm

do 15

16–25

pow. 25

sumaryczna długość
maksymalnie 25% łącznej
dopuszczalnej długości o
szerokości większej niż

P II

0,001–0,004 0,5 D

1,0 D

2,0 D

P III

0,002–0,006 0,5 D

1,0 D

2,0 D

0,004–0,006 mm

P IV

0,004–0,01

0,5 D

1,0 D

2,0 D

0,008–0,01 mm

P V

0,006–0,03

0,7 D

1,5 D

3,0 D

0,02–0,03 mm

P VI

0,006–0,05

0,75 D

1,5 D

3,0 D

0,03–0,05 mm

P VII

0,01–0,1

0,75 D

1,5 D

3,0 D

0,05–0,1 mm

Rysy o szerokości mniejszej od dolnej granicy nie bierze się pod uwagę, jeżeli nie tworzą

wyraźnie widocznej siatki.

Wymiarów skaz znajdujących się poza obszarem czynnym nie normalizuje się.
Szczerby na brzegach poza wymiarem czynnym są dopuszczalne jeżeli ich największy

wymiar nie przekracza 0,03 D, przy czym szczerby o wymiarach powyżej 0,5 mm powinny
być matowane.

Powierzchnię szczerby leżącą w obszarze czynnym przyrównuje się do punktu

i klasyfikuje w danej klasie czystości.

Przykłady:
Soczewka Ф 40 mm, Ф czynne 38 mm.
klasa P VII
Punkty 2,0 x 38 mm = 76 punktów o średnicy 0,3 do 2,0 mm, ale nie więcej niż 25% z 76 =
19 punktów dużych o średnicy większej niż 1,0 mm.

Rysy 3,0 x 38 mm = 114 mm łącznej długości rys o szerokości 0,01 do 0,1 mm, ale nie

więcej niż 25% z 114 = 28 mm rys o szerokości 0,05 do 0,1 mm

Maksymalna szczerba poza Ф czynnym 0,03 x 38 mm = 1,14 mm.
Soczewka fi 24 mm, fi czynne 23 mm.

klasa P IV
Punkty 1,2 x 23 mm = 27 punktów o średnicy 0,015 do 0,3 mm, ale nie więcej niż 25% z 27 =
6 punktów dużych o średnicy większej niż 0,1 mm.

Rysy 1,0 x 23 mm = 23 mm łącznej długości rys o szerokości 0,004 do 0,01 mm, ale nie

więcej niż 25% z 23 = 5 mm rys o szerokości 0,008 do 0,01 mm.

Maksymalna szczerba poza fi czynnym 0,03 x 23 mm = 0,69 mm.

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Co oznacza czystość powierzchni optycznej?

2.

Ile jest klas czystości?

3.

Jakich przyrządów optycznych używamy do sprawdzania czystości optycznej?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

36

4.3.3. Ćwiczenia

Ćwiczenie 1

Sprawdź czystość powierzchni płytki ogniskowej, soczewki ujemnej i płytki ochronnej

zgodnie z dokumentacją techniczną.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące czystości elementów
optycznych,

2)

zapoznać się dokładnie z normą dotyczącą czystości optycznej powierzchni elementów
optycznych,

3)

odczytać dokumentację techniczną otrzymanych elementów,

4)

zapoznać się ze stanowiskiem do sprawdzania czystości,

5)

dobrać sprzęt kontrolny,

6)

umyć dokładnie sprawdzane elementy,

7)

sprawdzić wygląd powierzchni zgodnie z wymaganiami normy,

8)

sprawdzić czystość badanych elementów,

9)

sporządzić notatkę.

Wyposażenie stanowiska pracy:

−

instrukcja stanowiskowa,

−

dokumentacja techniczna badanych elementów,

−

źródła światła, ekrany zgodnie z instrukcją,

−

lupy 4

x

, lupy 6

x

, lupa Brinella, mikroskop o powiększeniu min.10

x

i aperturze min. 0,3,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

−

pędzelki do odpylenia,

−

lampa sodowa,

−

norma dotycząca czystości elementów optycznych,

−

płytki ogniskowe, soczewki wklęsłe i płytki ochronne do pomiaru,

−

arkusz spostrzeżeń.

Ćwiczenie 2

Określ klasę czystości powierzchni otrzymanych elementów.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

wyszukać w materiałach dydaktycznych informacje dotyczące czystości elementów
optycznych,

2)

zapoznać się dokładnie z normą dotyczącą czystości optycznej powierzchni elementów
optycznych,

3)

zapoznać się ze stanowiskiem do sprawdzania czystości,

4)

dobrać sprzęt kontrolny,

5)

umyć dokładnie sprawdzane elementy,

6)

sprawdzić wygląd powierzchni zgodnie z wymaganiami normy,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

37

7)

określić klasę czystości badanych elementów,

8)

sporządź notatkę z wykonanego badania.

Wyposażenie stanowiska pracy:

−

instrukcja stanowiskowa,

−

źródła światła, ekrany zgodnie z instrukcją,

−

lupy 4

x

, lupy 6

x

, lupa Brinella, mikroskop o powiększeniu min. 10

x

i aperturze min. 0,3,

−

mieszanka spirytusowo-eterowa,

−

ściereczki batystowe,

−

pędzelki do odpylenia,

−

lampa sodowa,

−

norma dotycząca czystości elementów optycznych,

−

płytki ogniskowe, soczewki wklęsłe i płytki ochronne do pomiaru.

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

zdefiniować pojęcia czystości powierzchni elementów optycznych?

2)

scharakteryzować klasy czystości?

3)

dobrać przyrządy optyczne do badania czystości?

4)

określić klasę czystości zadanej powierzchni?

5)

sprawdzić czystość elementów optycznych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

38

5. SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

1.

Przeczytaj uważnie instrukcję.

2.

Podpisz imieniem i nazwiskiem kartę odpowiedzi.

3.

Zapoznaj się z zestawem zadań testowych.

4.

Test zawiera 25 zadania. Do każdego zadania dołączone są 4 możliwe odpowiedzi. Tylko
jedna jest prawidłowa.

5.

Udzielaj odpowiedzi na załączonej karcie odpowiedzi, stawiając w odpowiedniej rubryce
znak X. W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie
ponownie zakreślić odpowiedź prawidłową.

6.

Zadania wymagają stosunkowo prostych obliczeń, które powinieneś wykonać przed
wskazaniem poprawnego wyniku.

7.

Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.

8.

Jeśli udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego rozwiązanie
na później i wróć do niego, gdy zostanie Ci wolny czas.

9.

Na rozwiązanie testu masz 45 min.

Powodzenia

ZESTAW ZADAŃ TESTOWYCH

1. Współczynnik załamania szkła możemy zmierzyć za pomocą

a)

kolimatora.

b)

lunety.

c)

goniometru.

d)

lupy.

2.

Parametr odróżniający materiały optyczne to
a)

współczynnik załamania.

b)

niezmiennik załamania.

c)

zabarwienie.

d)

niezmiennik Keplera.

3.

Luneta autokolimacyjna służy do pomiaru
a)

dwójłomności.

b)

odchyłki kątów w pryzmatach.

c)

określenia czystości powierzchni.

d)

sprawdzenia pęcherzowatości.

4.

Kolimator wchodzi w skład układu do pomiaru
a)

smużystości.

b)

pęcherzowatości.

c)

dwójłomności.

d)

promienia soczewki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

39

5.

Naprężenia w elementach optycznych możemy sprawdzić za pomocą

a)

polarymetru.

b)

refraktometru.

c)

polaryskopu.

d)

szklanego sprawdzianu interferencyjnego.

6.

Do sprawdzania czystości optycznej używamy

a)

kolimatora.

b)

lupy 6

x

.

c)

lunety pomiarowej.

d)

teodolitu.

7.

Średnicę soczewki możemy zmierzyć za pomocą

a)

suwmiarki.

b)

szklanego sprawdzianu interferencyjnego.

c)

kątomierza.

d)

głębokościomierza.

8.

Szklanym sprawdzianem interferencyjnym możemy dokonać pomiaru

a)

średnicy soczewki.

b)

grubości soczewki.

c)

fazy soczewki.

d)

promienia krzywizny soczewki.

9.

Fazę w elementach optycznych możemy zmierzyć za pomocą

a)

suwmiarki.

b)

mikromierza.

c)

sferometru zegarowego.

d)

lupy Brinella.

10.

Sferometr służy do pomiaru

a)

grubości soczewki.

b)

promienia krzywizny zwierciadła.

c)

średnicy soczewki.

d)

płaskości płytki.

11.

Refraktometr Abbego to przyrząd służący do

a)

pomiaru współczynnika załamania szkła.

b)

refrakcji oka.

c)

zdolności rozdzielczej,

d)

współczynnik Abbego.

12.

Smużystość w szkle sprawdzamy w układzie

a)

źródło światła, stolik, ekran.

b)

kolimator, luneta.

c)

źródło światła, stolik, lupa.

d)

źródło światła, stolik, mikroskop pomiarowy.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

40

13.

Centralność soczewek sprawdzamy za pomocą układu

a)

źródło światła, stolik, ekran.

b)

kolimator, uchwyt mocujący, mikroskop pomiarowy.

c)

kolimator, uchwyt mocujący, luneta autokolimacyjna.

d)

źródło światła, stolik, lupa.

14.

Ława optyczna może służyć do

a)

zestawiania układów pomiarowych.

b)

badania naprężeń.

c)

sprawdzania płaskości.

d)

sprawdzania czystości elementów optycznych.

15.

Przedstawiony schemat pomiarowy służy do

a)

pomiaru promienia.

b)

sprawdzenia smużystości.

c)

sprawdzenia pęcherzowatości.

d)

pomiarów kątów.

16.

Przedstawiony schemat pomiarowy służy do

a)

pomiaru promienia.

b)

sprawdzenia smużystości.

c)

sprawdzenia pęcherzowatości.

d)

pomiarów kątów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

41

17.

Przedstawiony schemat pomiarowy służy do

a)

pomiaru promienia.

b)

pomiaru ogniskowej.

c)

średnicy soczewki.

d)

pomiarów kątów.

18.

Przedstawiony schemat pomiarowy służy do

a)

pomiaru promienia.

b)

pomiaru kąta odchylenia klina.

c)

pomiaru centralności soczewki.

d)

pomiarów ogniskowych.

19.

Pryzmat Amici zamontowany jest w
a)

refraktometrze Pulfricha.

b)

refraktometrze Abbego.

c)

sferometrze.

d)

goniometrze.

20.

Zjawisko całkowitego wewnętrznego odbicia wykorzystane jest do budowy
a)

sferometru

b)

goniometru.

c)

refraktometru.

d)

kolimatora.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

42

21.

Schemat pokazany na rysunku służy do

a)

pomiaru promienia.

b)

badania powierzchni płaskich.

c)

badania zdolności rozdzielczej.

d)

pomiaru kąta.

22.

Symbol PV określa klasę
a)

czystości.

b)

pęcherzowatości.

c)

smużystości.

d)

niejednorodności.

23.

Do sprawdzania bardzo dokładnych powierzchni płaskich wykorzystujemy
a)

interferencji jednopromieniowej.

b)

interferencji dwupromieniowej.

c)

interferencji trójpromieniowej.

d)

interferencji wielopromieniowej.

24.

Przedstawiony wzór

y

k

f

′

⋅

=

służy do wyznaczania

a)

ogniskowej badanego elementu optycznego.

b)

ogniskowej kolimatora kontrolnego.

c)

ogniskowej lunety pomiarowej.

d)

ogniskowej mikroskopu kontrolnego.

25.

Pokazane kątowniki do pomiaru pryzmatów wykonane są

a)

z mosiądzu.

b)

ze stali.

c)

ze szkła.

d)

z tworzywa sztucznego.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

43

KARTA ODPOWIEDZI

Imię i nazwisko..........................................................................................

Dokonywanie pomiarów elementów optycznych

Zakreśl poprawną odpowiedź, wpisz brakujące części zdania lub wykonaj rysunek

Nr

zadania

Odpowiedź

Punkty

1

a

b

c

d

2

a

b

c

d

3

a

b

c

d

4

a

b

c

d

5

a

b

c

d

6

a

b

c

d

7

a

b

c

d

8

a

b

c

d

9

a

b

c

d

10

a

b

c

d

11

a

b

c

d

12

a

b

c

d

13

a

b

c

d

14

a

b

c

d

15

a

b

c

d

16

a

b

c

d

17

a

b

c

d

18

a

b

c

d

19

a

b

c

d

20

a

b

c

d

21

a

b

c

d

22

a

b

c

d

23

a

b

c

d

24

a

b

c

d

25

a

b

c

d

Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

44

6.

LITERATURA

1.

Chalecki J: Przyrządy optyczne. WNT, Warszawa 1979

2.

Hanc T: Pomiary Optyczne. WNT, Warszawa 1964

3.

Jóźwicki R: Optyka Instrumentalna. WNT, Warszawa 1970

4.

Krawcow J. A., Orłow J. I: Optyka geometryczna ośrodków jednorodnych. WNT,
Warszawa 1993

5.

Legun Z: Technologia elementów optycznych. WNT, Warszawa 1982

6.

Meyer – Arendt J. R: Wstęp do optyki. PWN, Warszawa 1977

7.

Nowak J., Zając M: Optyka – kurs elementarny. Oficyna Wydawnicza Politechniki
Wrocławskiej, Wrocław 1998

8.

Pluta M: Mikroskopia optyczna. PWN, Warszawa 1982

9.

Sojecki A: Optyka. WSiP, Warszawa 1997

10.

Szymański J: Budowa i montaż aparatury optycznej. WSiP, Warszawa 1978

11.

Tryliński W. (red.): Konstrukcja przyrządów i urządzeń precyzyjnych. WNT, Warszawa
1996