Ć
wiczenie 5
Temat: Rozwiązywanie równań stanu i wyjścia układów automatyki
przy zadanych warunkach początkowych dla stanu ustalonego i
nieustalonego.
Przykład 1
Dla stanu ustalonego układu regulacji automatycznej (URA) przy
zadanym warunku początkowym
( )
[ ]
T
0
1
0
x
=
wyznaczyć rozwiązanie
równania stanu oraz podać równanie wyjścia.
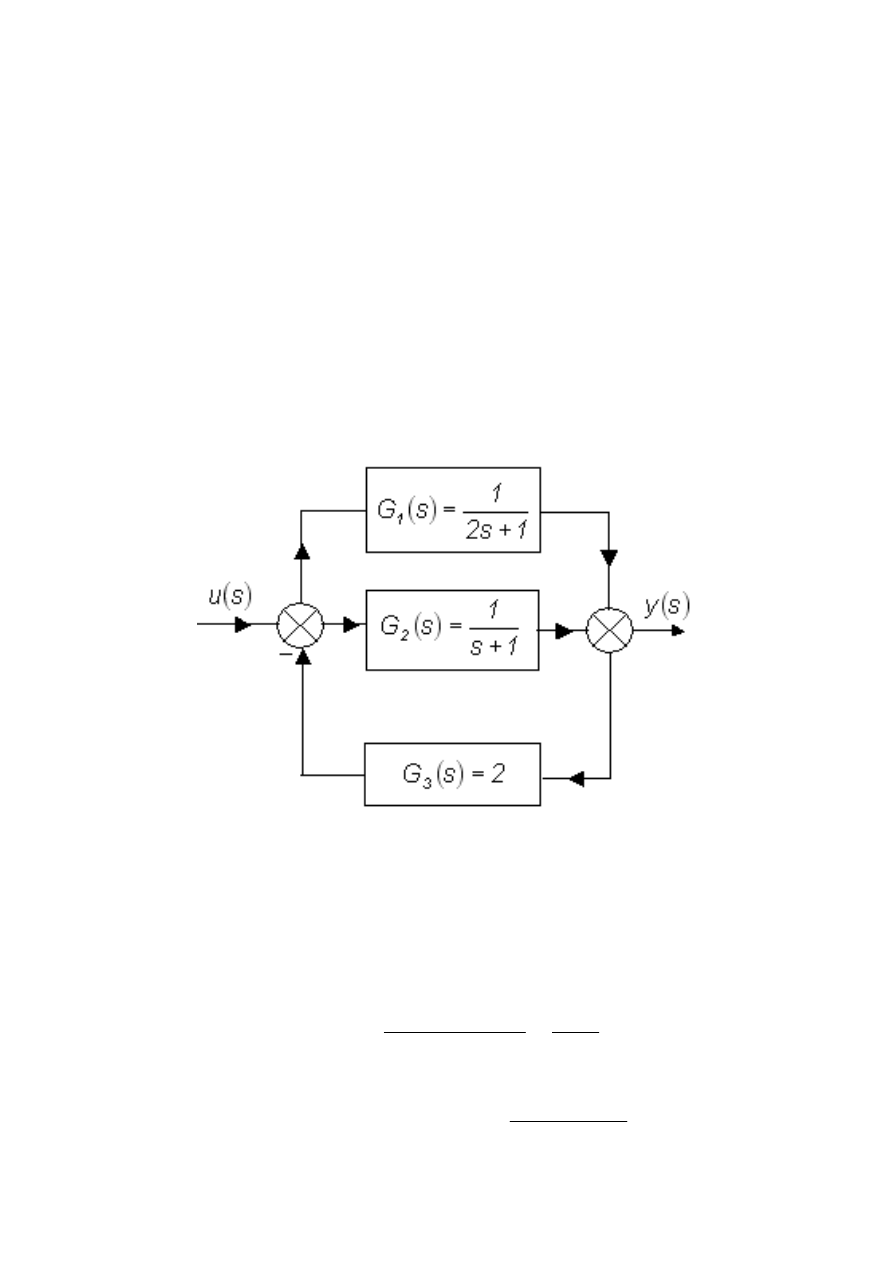
Rys.1.
Schemat blokowy (strukturalny) badanego URA
R o z w i ą z a n i e
Należy wyznaczyć transmitancję badanego układu automatyki, zatem
( )
( )
( ) ( )
3
s
1
s
G
s
G
1
s
G
s
G
3
2
2
3
,
2
+
=
+
=
( )
( )
( )
3
s
7
s
2
4
s
3
s
G
s
G
s
G
2
3
,
2
1
z
+
+
+
=
+
=

Wybieramy metodę bezpośrednią, stąd przy najwyższej potędze
przy s musi być współczynnik równy jedności, zatem
( )
(
)(
)
5
.
0
s
3
s
2
s
5
.
1
5
.
1
s
5
.
3
s
2
s
5
.
1
s
G
2
z
+
+
+
=
+
+
+
=
Współczynniki równania stanu i wyjścia są następujące
5
.
1
a
0
=
,
5
.
3
a
1
=
,
2
b
0
=
,
5
.
1
b
1
=
Równania stanu w zapisie ogólnym są
( )
( )
t
x
t
x
2
1
=
&
( )
( )
( ) ( )
( )
( ) ( )
t
u
t
x
5
.
3
t
x
5
.
1
t
u
t
x
a
t
x
a
t
x
2
1
2
1
1
0
2
+
−
−
=
+
−
−
=
&
Równanie wyjścia przyjmuje postać
( )
( )
( )
( )
2
1
2
1
1
0
n
0
i
1
i
i
x
5
.
1
x
2
t
x
b
t
x
b
t
x
b
t
y
+
=
+
=
∑
=
=
+
Macierze równania stanu w zapisie macierzowo-wektorowym są
następujące
−
−
=
5
.
3
5
.
1
1
0
A
,
=
1
0
B
macierz jednostkowa
=
s
0
0
s
SI
,
+
−
=
−
−
−
=
−
5
.
3
s
5
.
1
1
s
5
.
3
5
.
1
1
0
s
0
0
s
A
SI
Macierz algebraicznych dopełnień jest
[
]
+
=
−
s
5
.
1
1
5
.
3
s
A
SI
adj
,
zaś wyznacznik z macierzy
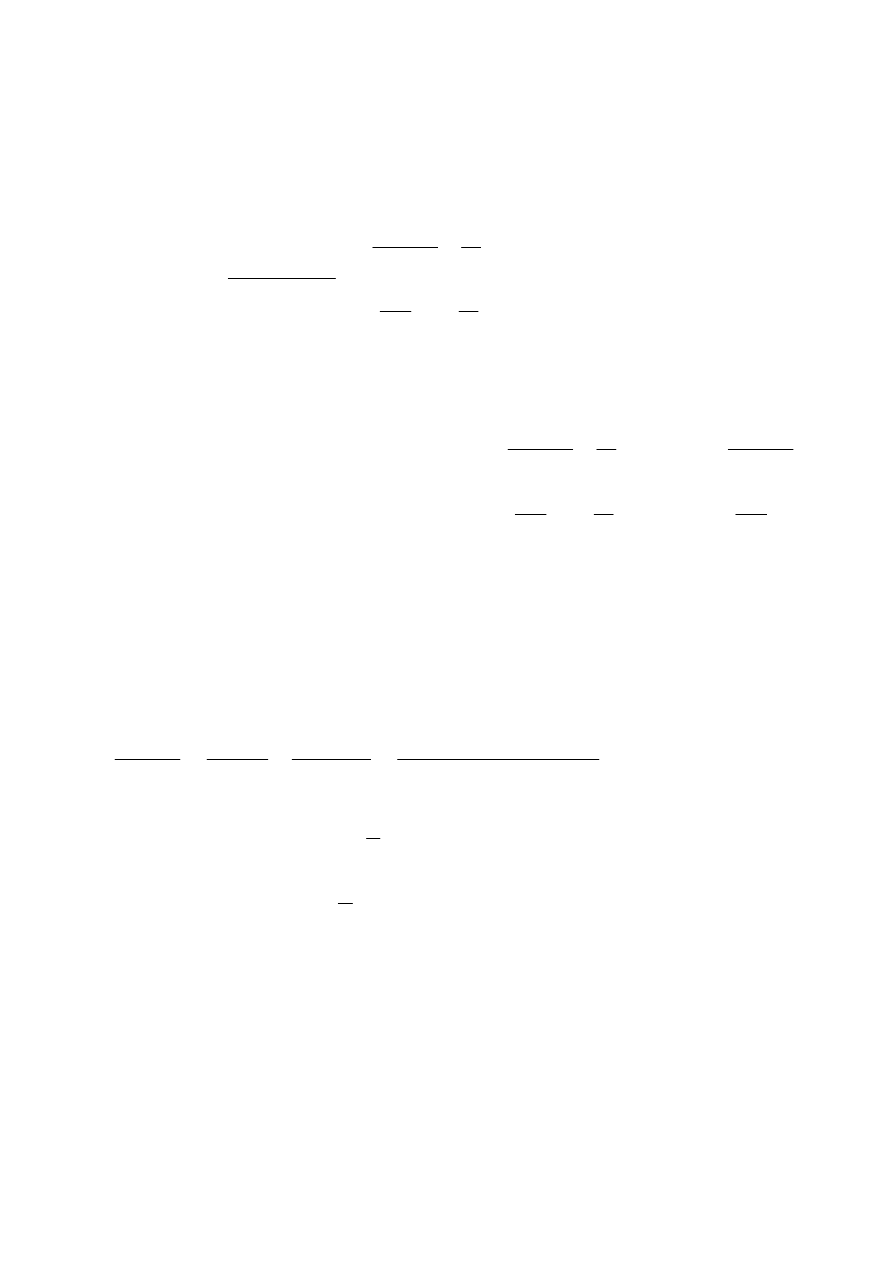
[
]
(
)
(
)(
)
m
5
.
0
s
3
s
5
.
1
s
5
.
3
s
5
.
1
5
.
3
s
s
A
SI
det
2
=
+
+
=
+
+
=
+
+
=
−
Macierz odwrotna wynosi
[
]
[
]
[
]
+
=
−
−
=
−
−
m
s
m
5
.
1
m
1
m
5
.
3
s
A
SI
det
A
SI
adj
A
SI
1
Zatem rozwiązanie równania stanu można przedstawić w postaci
( )
( )
(
)
[
]
( )
+
=
+
=
−
=
=
−
−
−
−
m
5
.
1
m
5
.
3
s
L
0
1
m
s
m
5
.
1
m
1
m
5
.
3
s
L
0
x
A
SI
L
0
x
e
t
x
1
1
1
1
At
Z tablic Laplace’a nie można bezpośrednio odczytać funkcji
obrazującej rozwiązanie, dlatego też należy dokonać rozkładu
wyrazów macierzy na ułamki proste, czyli
(
) (
)
(
)
m
B
3
A
5
.
0
B
A
s
5
.
0
s
B
3
s
A
m
5
.
3
s
+
+
+
=
+
+
+
=
+
, stąd
5
6
B
5
.
3
B
3
A
5
.
0
5
1
B
1
A
1
B
A
=
⇒
=
+
−
=
−
=
⇒
=
+

(
) (
)
(
)
m
B
3
A
5
.
0
B
A
s
5
.
0
s
B
3
s
A
m
5
.
1
+
+
+
=
+
+
+
=
, stąd
3
5
B
5
.
1
B
3
A
5
.
0
3
5
B
A
0
B
A
=
⇒
=
+
−
=
−
=
⇒
=
+
Ostatecznie posługując się tablicami przekształceń Laplace’a
otrzymamy
( )
(
) (
)
(
) (
)
+
−
+
−
=
+
+
+
−
+
+
+
−
=
+
=
−
−
−
−
−
−
t
5
.
0
t
3
t
5
.
0
t
3
1
1
e
3
5
e
3
5
e
5
6
e
5
1
5
.
0
s
3
5
3
s
3
5
5
.
0
s
5
6
3
s
5
1
L
m
5
.
1
m
5
.
3
s
L
t
x
Przykład 2
Określić rozwiązanie równania wyjścia
( )
t
y
na sterowanie
( ) ( )
t
1
t
u
=
układu URA o transmitancji
( )
1
.
0
s
7
.
0
s
10
s
G
2
+
+
=
R o z w i ą z a n i e
Współczynniki licznika i mianownika transmitancji
( )
s
G
są
następujące
0
b
,
10
b
,
7
.
0
a
,
1
.
0
a
1
0
1
0
=
=
=
=
Zależność na transmitancję układu w zapisie macierzowo-
wektorowym jest następująca
( ) ( )
( )
[
]
( )
[
]
( )
( )
s
Du
s
Bu
A
SI
C
s
y
D
B
A
SI
C
s
u
s
y
s
G
1
1
+
−
=
⇒
+
−
=
=
−
−

gdzie:
−
D
,
C
macierze równania wyjścia w zapisie macierzowo-
wektorowym,
−
B macierz równania wejścia w zapisie
macierzowo-wektorowym,
( )
−
s
u
sygnał sterujący (wejściowy)
Równanie wyjścia w zapisie macierzowo-wektorowym przyjmuje
postać
( )
( )
( )
t
Du
t
Cx
t
y
+
=
lub w zapisie ogólnym
( )
( )
( )
( )
1
2
1
1
0
n
0
i
1
i
i
x
10
t
x
b
t
x
b
t
x
b
t
y
=
+
=
∑
=
=
+
Postać równań stanu w zapisie ogólnym jest następująca
( )
( )
t
x
t
x
2
1
=
&
( )
( )
( ) ( )
( )
( ) ( )
t
u
t
x
7
.
0
t
x
1
.
0
t
u
t
x
a
t
x
a
t
x
2
1
2
1
1
0
2
+
−
−
=
+
−
−
=
&
zatem macierze
D
,
C
,
B
,
A
są następujące
−
−
=
7
.
0
1
.
0
1
0
A
,
=
1
0
B
,
[
]
0
10
C
=
,
0
D
=
[
]
+
−
=
−
−
−
=
−
7
.
0
s
1
.
0
1
s
7
.
0
1
.
0
1
0
s
0
0
s
A
SI
,
[
]
−
+
=
−
s
1
.
0
1
7
.
0
s
A
SI
adj
,
[
]
(
)
(
)(
)
m
2
.
0
s
5
.
0
s
1
.
0
7
.
0
s
s
A
SI
det
=
+
+
=
+
+
=
−

[
]
[
]
[
]
−
+
=
−
−
=
−
−
m
s
m
1
.
0
m
1
m
7
.
0
s
A
SI
det
A
SI
adj
A
SI
1
( )
[
]
( )
( )
[
]
(
)(
)
2
.
0
s
5
.
0
s
s
10
m
1
s
10
s
1
m
s
m
1
.
0
m
1
m
7
.
0
s
1
0
0
10
s
Du
s
Bu
A
SI
C
s
y
1
+
+
=
=
=
−
+
=
+
−
=
−
Zatem
Ponieważ nie można bezpośrednio skorzystać z tablic Laplace’a,
więc funkcję
( )
s
y
należy rozłożyć na ułamki proste, zatem
( )
(
)(
)
+
+
+
+
=
+
+
=
−
−
2
.
0
s
C
5
.
0
s
B
s
A
L
2
.
0
s
5
.
0
s
s
10
L
t
y
1
1
(
)(
)
(
)(
)
(
)
(
)
(
)(
)
(
) (
)
(
)(
)
2
.
0
s
5
.
0
s
s
A
1
.
0
C
5
.
0
B
2
.
0
A
7
.
0
s
C
B
A
s
2
.
0
s
5
.
0
s
s
5
.
0
s
Cs
2
.
0
s
Bs
2
.
0
s
5
.
0
s
A
2
.
0
s
C
5
.
0
s
B
s
A
2
.
0
s
5
.
0
s
s
10
2
+
+
+
+
+
+
+
+
=
=
+
+
+
+
+
+
+
+
=
=
+
+
+
+
=
+
+
Współczynniki
C
,
B
,
A
rozkładu funkcji na ułamki proste
wyznaczymy z następującego układu równań algebraicznych

stąd
3
500
C
,
3
200
B
,
100
A
10
A
1
.
0
0
C
5
.
0
B
2
.
0
A
7
.
0
0
C
B
A
−
=
=
=
⇒
=
=
+
+
=
+
+
Ostatecznie na podstawie tablic Laplace’a otrzymamy
( )
(
) (
)
+
−
=
+
−
+
+
=
−
−
−
t
5
.
0
t
2
.
0
1
e
3
2
e
3
5
1
100
2
.
0
s
3
500
5
.
0
s
3
200
s
100
L
t
y
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 3 pow
Ćwiczenie 5 pow
Ćwiczenie 4 pow
Ćwiczenie 2 pow
Ćwiczenie 3 pow
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
więcej podobnych podstron