Ćwiczenie 3
Temat: Badanie stabilności złożonego układu automatyki przy
zastosowaniu logarytmicznego kryterium Nyquista.
Przykład 1
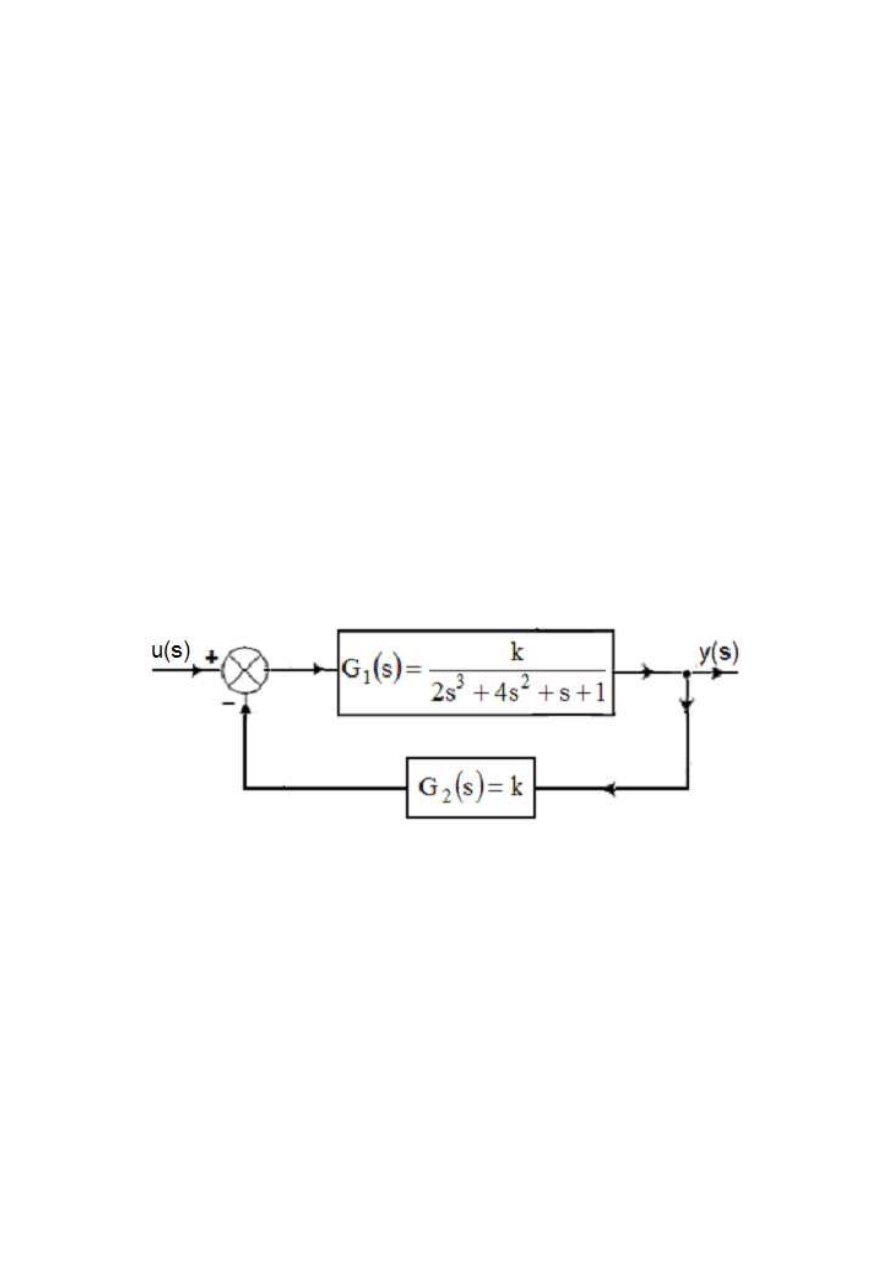
W przedstawionym na rysunku 1
układzie automatyki,
wyznaczyć funkcję zmiany zapasu modułu układu otwartego w
funkcji wzmocnienia
k
. Obliczyć jaka będzie maksymalna amplituda
sygnału wejściowego odpowiedzi w układzie zamkniętym, jeśli
przesunięcie fazowe
o
0
=
ϕ
,
5
.
0
k
=
, zaś amplituda wymuszenia
.
cm
3
x
0
=
Rys.1. Schemat układu automatyki
R o z w i ą z a n i e
Transmitancja widmowa, zastępcza otwartego układu automatyki jest

( )
( )
( )
(
) (
)
[
]
(
) (
)
[
]
(
) (
)
[
]
(
) (
)
[
]
(
)
(
)
[
]
(
)
(
)
(
)
[
]
(
)
(
)
(
)
[
]
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
2
o
2
1
4
1
2
1
j
2
1
4
1
4
1
k
2
1
4
1
2
1
j
4
1
k
2
1
j
4
1
2
1
j
4
1
2
1
j
4
1
k
1
j
j
4
j
2
k
j
G
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
+
−
−
−
−
+
−
−
=
=
−
+
−
−
−
−
=
=
−
−
−
−
+
−
−
−
−
=
=
+
+
+
=
Część rzeczywista
( )
ω
P
i urojona
( )
ω
Q
.
( )
(
)
(
)
(
)
[
]
2
2
2
2
2
2
2
2
1
4
1
4
1
k
P
ω
ω
ω
ω
ω
−
+
−
−
=
,
( )
(
)
(
)
(
)
[
]
2
2
2
2
2
2
2
1
4
1
2
1
Q
ω
ω
ω
ω
ω
ω
−
+
−
−
−
=
.
Zapas modułu
( )
(
)
(
)
(
)
[
]
[ ]
s
1
5
.
0
0
2
1
4
1
2
1
Q
2
2
2
2
2
2
=
→
=
−
+
−
−
−
=
ω
ω
ω
ω
ω
ω
ω
,
(
)
2
k
5
.
0
P
=
=
ω
,
(
)
2
k
1
5
.
0
P
1
M
−
=
=
−
=
ω
∆
.
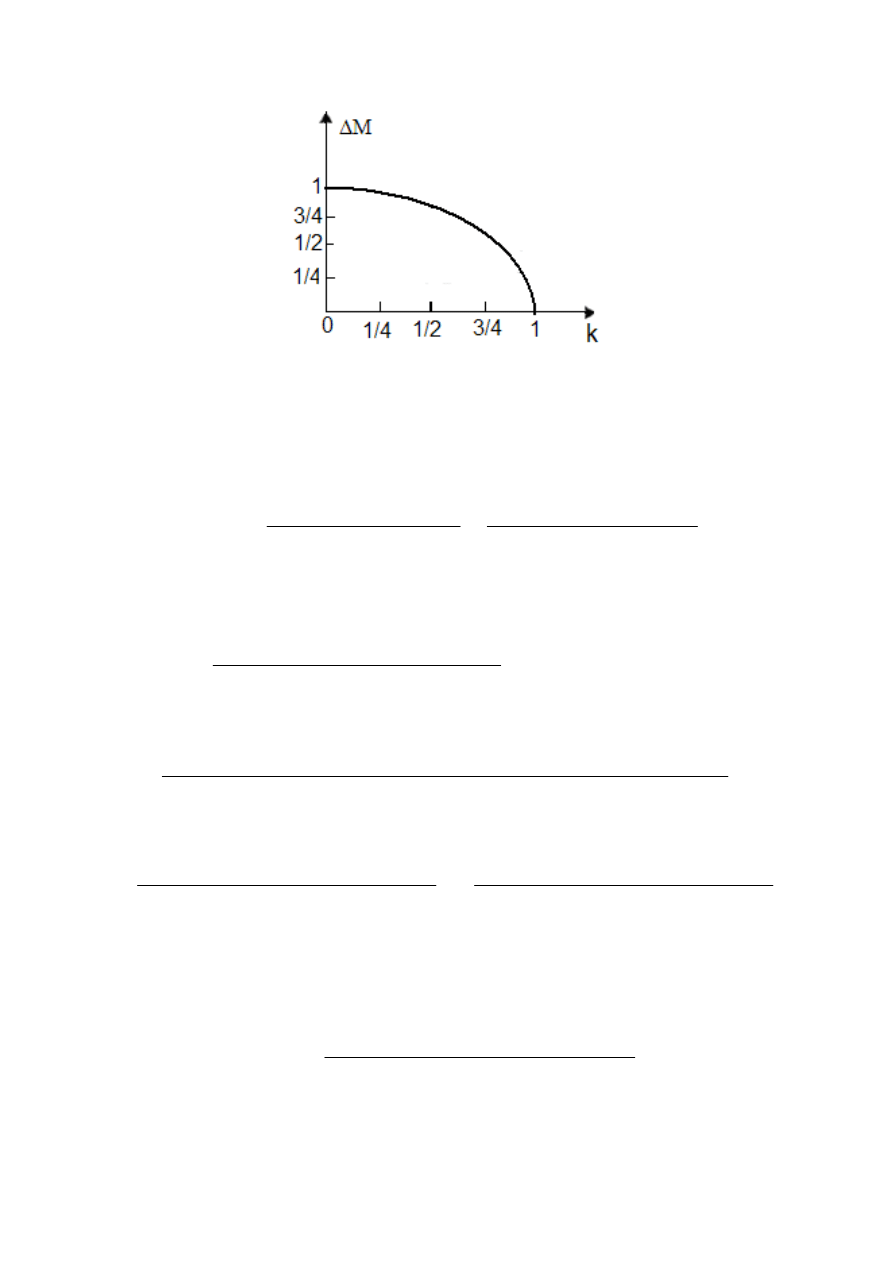
Rys.2. Wykres zmiany modułu w funkcji współczynnika wzmocnienia
k
Transmitancja operatorowa badanego układu automatyki jest
( )
( ) ( )
( ) ( ) ( )
2
2
3
3
2
1
2
1
z
k
1
s
s
4
s
2
k
s
G
s
G
s
G
1
s
G
s
G
s
G
+
+
+
+
=
+
=
,
Transmitancja widmowa
( )
( )
( )
(
)
[
]
(
)
{
}
(
)
[
]
(
)
{
}(
)
[
]
(
)
(
)
[
]
(
)
[
]
(
)
(
)
(
)
[
]
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
z
2
1
4
k
1
2
1
k
j
2
1
4
k
1
4
k
1
k
2
1
j
4
k
1
2
1
j
4
k
1
2
1
j
4
k
1
k
k
1
j
j
4
j
2
k
j
G
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
+
−
+
−
−
−
+
−
+
−
+
=
=
−
−
−
+
−
+
−
+
−
−
−
+
=
=
+
+
+
+
=
Część rzeczywista
( )
ω
P
i urojona
( )
ω
Q
.
( )
(
)
[
]
(
)
[
]
(
)
2
2
2
2
2
2
2
2
2
1
4
k
1
4
k
1
k
Q
ω
ω
ω
ω
ω
−
+
−
+
−
+
=
,
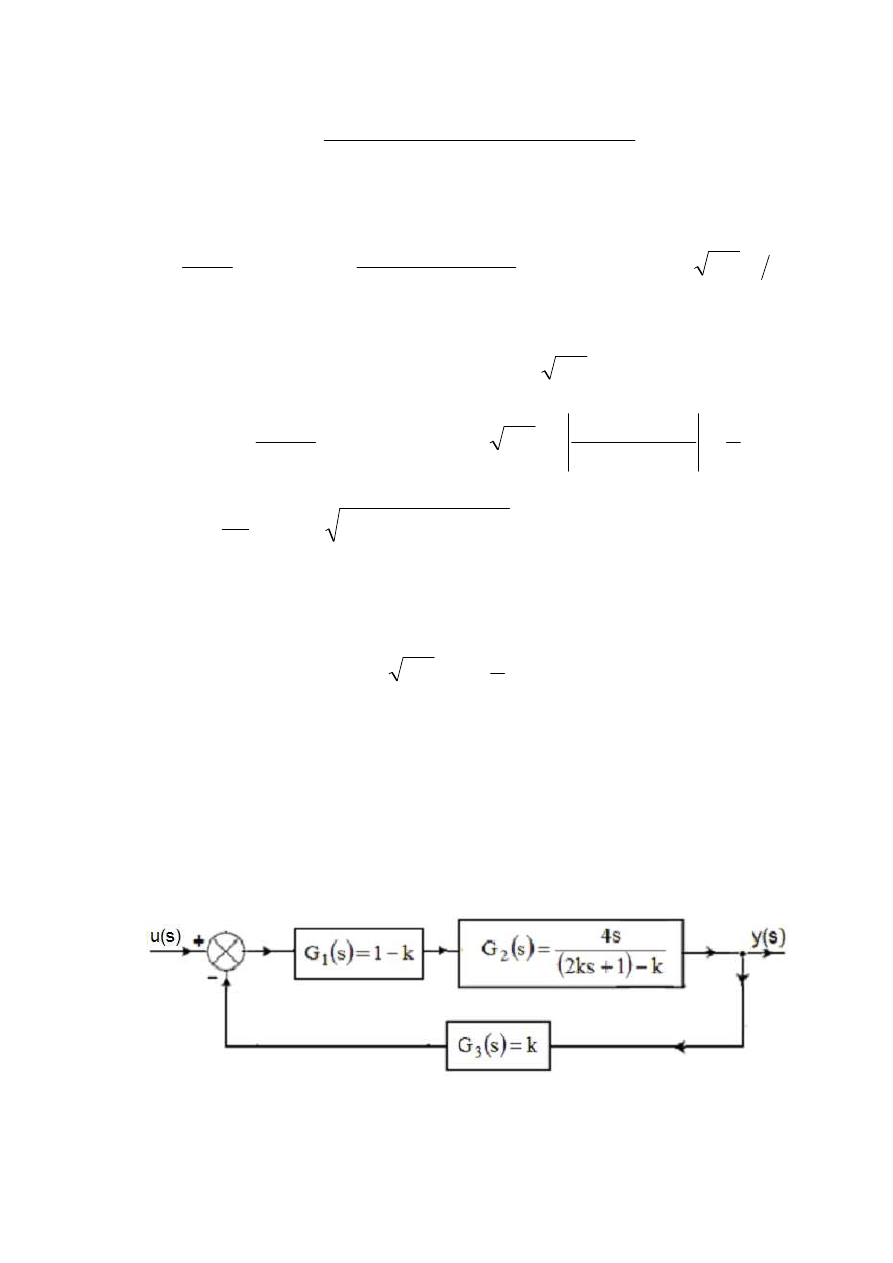
( )
(
)
(
)
[
]
(
)
2
2
2
2
2
2
2
2
1
4
k
1
2
1
k
P
ω
ω
ω
ω
ω
ω
−
+
−
+
−
=
,
( )
( )
(
)
(
)
[
]
[ ]
s
1
5
.
0
,
0
4
k
1
k
2
1
k
0
tan
P
Q
tan
2
1
2
2
2
=
=
→
−
+
−
−
=
=
=
ω
ω
ω
ω
ω
ω
ω
ϕ
o
,
(
)
,
0
0
Q
=
=
ω
(
)
0
5
.
0
Q
=
=
ω
,
(
)
4
.
0
k
1
k
0
P
2
=
+
=
=
ω
,
(
)
3
2
4
k
1
k
5
.
0
P
2
2
=
−
+
=
=
ω
ω
,
( )
( )
[
]
( )
[
]
( )
( )
0
0
2
2
0
0
x
P
y
P
Q
P
M
x
y
j
G
ω
ω
ω
ω
ω
=
→
=
+
=
=
=
,
dla
(
)
[ ]
cm
2
.
1
3
4
.
0
x
0
P
y
0
0
=
⋅
=
=
=
ω
,
(
)
[ ]
cm
2
3
3
2
x
5
.
0
P
y
0
0
=
⋅
=
=
=
ω
.
Przykład 2
Dla układu automatyki którego schemat przedstawia rysunek 3.
Określić współczynnik wzmocnienia
k
, dla którego istnieje zapas
modułu.
Rys.3. Schemat układu automatyki

R o z w i ą z a n i e
Transmitancja zastępcza układu automatyki jest
( )
( ) ( )
( ) ( ) ( )
(
)
(
)
k
1
s
k
2
k
4
s
k
4
k
1
s
4
s
G
s
G
s
G
1
s
G
s
G
s
G
2
2
3
2
1
2
1
z
−
+
−
+
−
=
+
=
,
Równanie charakterystyczne
(
)
,
0
k
1
s
k
2
k
4
s
k
4
2
2
=
−
+
−
+
,
1
k
0
k
1
a
0
<
→
>
−
=
(
)
,
2
k
i
0
k
0
k
2
k
4
a
1
<
>
→
>
−
=
0
k
0
k
4
a
2
2
>
→
>
=
,
2
k
0
<
<
Dla układu otwartego
( )
=
s
G
o
( ) ( ) ( )
s
G
s
G
s
G
3
2
1
=
(
)
(
)
k
1
ks
2
s
k
1
k
4
2
−
+
−
,
Transmitancja widmowa
( )
ω
j
G
o
( )
(
)
(
) (
)
[
]
{
}
(
)
[
]
{
}
(
)
[
]
{
}
(
)
(
) (
)
[
]
{
}
(
)
[
]
{
}
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
o
k
16
k
4
k
1
k
4
k
1
k
1
k
4
j
k
1
k
16
k
4
j
k
4
k
1
k
4
j
k
4
k
1
k
4
j
k
4
k
1
j
k
1
k
4
k
1
k
4
j
k
4
j
k
1
k
4
j
G
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
−
−
−
+
−
=
=
−
−
−
+
−
−
−
−
−
−
=
=
−
+
+
−
−
=
Część rzeczywista
( )
ω
P
i urojona
( )
ω
Q
.
( )
(
)
(
)
[
]
{
}
2
2
2
2
2
2
2
k
16
k
4
k
1
k
1
k
16
P
ω
ω
ω
ω
+
−
−
−
=
,

( )
(
) (
)
[
]
{
}
(
)
[
]
{
}
2
2
2
2
2
2
2
k
16
k
4
k
1
k
4
k
1
k
1
k
4
Q
ω
ω
ω
ω
ω
+
−
−
−
−
−
=
.
( )
(
) (
)
[
]
{
}
(
)
[
]
{
}
(
) (
)
[
]
{
}
0
k
4
k
1
k
1
k
4
0
k
16
k
4
k
1
k
4
k
1
k
1
k
4
Q
2
2
2
2
2
2
2
2
2
=
−
−
−
→
→
=
+
−
−
−
−
−
=
ω
ω
ω
ω
ω
ω
ω
,
stąd
k
1
k
2
1
−
=
ω
,
k
1
4
k
1
k
2
1
P
−
=
−
=
ω
,
5
k
0
k
1
4
1
k
1
k
2
1
P
1
M
>
→
>
−
−
=
−
=
−
=
ω
∆
.
Aby istniał zapas modułu to współczynnik wzmocnienia
k
musi być
większy od 5.
Przykład 3
Zbadać stabilność układu i określić zapas modułu i zapas fazy układu
zamkniętego korzystając z logarytmicznego kryterium Nyquista.
Transmitancja operatorowa układu otwartego ma postać
( ) (
)(
)(
) (
)(
)(
)
( )
( )
,
s
N
s
M
1
s
1
.
0
1
s
1
s
10
10
1
s
T
1
s
T
1
s
T
k
s
G
0
0
4
3
2
0
=
+
+
+
=
+
+
+
=

Równanie charakterystyczne układu otwartego ma postać
( ) (
)(
)(
)
0
1
s
1
.
0
1
s
1
s
10
s
N
0
=
+
+
+
=
( )
0
1
s
1
,
11
s
1
,
11
s
s
N
2
3
0
=
+
+
+
=
Sprawdzamy stabilność układu otwartego korzystając z kryterium
Hurwitza
Warunek konieczny
n
,......
3
,
2
,
1
i
,
0
a
i
=
>
1
a
,
1
.
11
a
,
1
.
11
a
,
1
a
3
2
1
0
=
=
=
=
Warunek dostateczny
1
n
0
n
a
−
=
∆
∆
0
2
.
122
1
1
.
11
1
.
11
1
.
11
1
1
1
.
11
a
a
a
a
1
0
3
2
2
>
=
−
⋅
=
=
=
∆
Tak więc układ otwarty jest stabilny.
Aby po zamknięciu układ był stabilny, kryterium Nyquista wymaga,
aby charakterystyka amplitudowa układu otwartego
( )
ω
j
G
0
nie
obejmowała punktu
(
)
0
j
,
1
−
dla częstości
( )
∞
∈
,
0
ω
. Z kryterium
Nyquista wynika warunek stabilności
(
)
1
j
G
0
<
−
π
ω
gdzie
π
ω
−
jest częstością, dla której kąt przesunięcia fazowego jest
(
)
o
180
j
G
arg
0
−
=
−
π
ω

Jeżeli charakterystyka częstotliwościowa jest przedstawiona w postaci
logarytmicznych charakterystyk amplitudowej
( )
ω
L
i fazowej
( )
ω
ϕ
, to
warunek stabilności przyjmuje postać
( )
(
)
0
j
G
log
20
L
0
<
=
−
−
π
π
ω
ω
Kryterium to można sformułować następująco
Jeżeli charakterystyka amplitudowa układu otwartego ma
wartość ujemną dla częstości odpowiadającej przesunięciu
fazowemu
( )
o
180
−
=
−
π
ω
ϕ
to układ po zamknięciu będzie stabilny.
( ) (
)(
)(
)
,
1
j
1
.
0
1
j
1
j
10
10
j
G
0
+
+
+
=
ω
ω
ω
ω
1) Transmitancję widmową przedstawimy w postaci iloczynu
transmitancji podstawowych elementów automatyki tj.
( )
( )
( ) ( )
( )
ω
ω
ω
ω
ω
j
G
j
G
j
G
j
G
j
G
4
3
2
1
0
⋅
⋅
⋅
=
gdzie
( )
−
=
10
j
G
1
ω
transmitancja elementu proporcjonalnego,
10
k
=
( )
−
+
=
1
j
10
1
j
G
2
ω
ω
transmitancja elementu inercyjnego pierwszego
rzędu
sek
10
T
2
=
( )
−
+
=
1
j
1
j
G
3
ω
ω
transmitancja elementu inercyjnego pierwszego
rzędu
sek
1
T
3
=
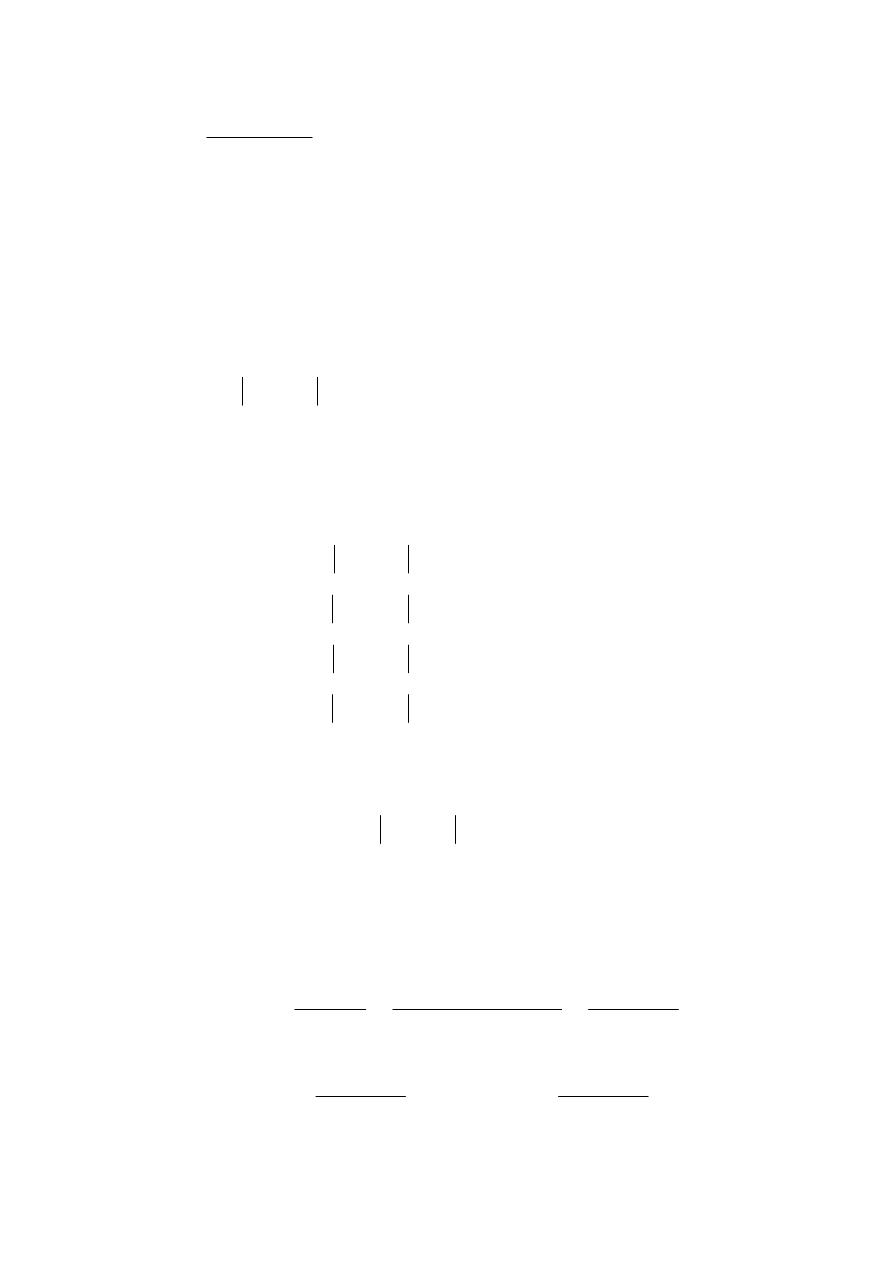
( )
−
+
=
1
j
10
.
0
1
j
G
4
ω
ω
transmitancja
elementu
inercyjnego
pierwszego rzędu
sek
10
.
0
T
4
=
2) Transmitancję układu otwartego można wyznaczyć z
charakterystyk logarytmicznych: amplitudowej i fazowej z
następujących zależności
( )
( )
( )
( )
( )
( )
[ ]
dB
?
L
L
L
L
L
j
G
log
20
L
4
3
2
1
0
=
⇒
+
+
+
=
=
∆
ω
ω
ω
ω
ω
ω
( )
( )
( )
( )
( )
( )
[ ]
o
?
j
G
arg
4
3
2
1
o
=
⇒
+
+
+
=
=
φ
∆
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ϕ
gdzie
( )
( )
( )
( )
ω
ω
ϕ
ω
ω
j
G
arg
,
j
G
log
20
L
1
1
1
1
=
=
( )
( )
( )
( )
ω
ω
ϕ
ω
ω
j
G
arg
,
j
G
log
20
L
2
2
2
2
=
=
( )
( )
( )
( )
ω
ω
ϕ
ω
ω
j
G
arg
,
j
G
log
20
L
3
3
3
3
=
=
( )
( )
( )
( )
ω
ω
ϕ
ω
ω
j
G
arg
,
j
G
log
20
L
4
4
4
4
=
=
Dla elementu proporcjonalnego
( )
( )
dB
20
10
log
20
j
G
log
20
L
1
1
=
=
=
ω
ω
( )
o
0
1
=
ω
ϕ
Dla elementu inercyjnego pierwszego rzędu o transmitancji
( )
(
)(
)
2
2
T
1
jT
1
1
Tj
1
Tj
1
Tj
1
Tj
1
j
G
ω
ω
ω
ω
ω
ω
ω
+
−
=
−
+
−
=
+
=
,
( )
2
2
T
1
1
P
ω
ω
+
=
,
( )
2
2
T
1
T
Q
ω
ω
ω
+
−
=
.
( )
( )
( )
[
]
( )
[
]
,
T
1
1
log
20
Q
P
log
20
A
log
20
L
2
2
2
2
ω
ω
ω
ω
ω
+
=
+
=
=
( )
2
2
T
1
log
20
L
ω
ω
+
−
=
,
( )
( )
( )
( )
ω
ω
ω
ω
ϕ
T
tg
arc
P
Q
tg
arc
−
=
=
.
1)
Aproksymowane charakterystyki logarytmiczne amplitudowa i
fazowa:
Dla
T
1
1
T
s
s
=
→
=
ω
ω
jest
( )
log
20
L
−
=
ω
1
2
s
+
ω
ω
,
( )
−
=
s
tg
arc
ω
ω
ω
ϕ
.
Stąd dla:
1
s
<
ω
ω
( )
0
L
=
ω
,
( )
0
=
ω
ϕ
, dla
1
.
0
s
<
ω
ω
dla:
1
s
>
ω
ω
( )
s
log
20
L
ω
ω
ω
−
=
,
( )
o
90
−
=
ω
ϕ
, dla
s
ω
ω
>10
( )
ω
ϕ
jest sieczną przechodzącą przez punkty o współrzędnych
=
=
0
,
1
.
0
s
ϕ
ω
ω
i
−
=
=
o
90
,
10
s
ϕ
ω
ω
dla
10
1
.
0
s
≤
≤
ω
ω
Częstości sprzęgające
s
ω
są następujące:
=
=
=
s
rad
1
.
0
10
1
T
1
2
2
s
ω
,

=
=
=
s
rad
1
1
1
T
1
3
3
s
ω
,
=
=
=
s
rad
10
1
.
0
1
T
1
4
4
s
ω
.
( )
s
/
rad
1
.
0
dla
dB
0
L
2
<
=
ω
ω
( )
s
/
rad
1
.
0
dla
dB
10
log
20
1
.
0
log
20
L
2
>
−
=
−
=
ω
ω
ω
ω
( )
s
/
rad
01
.
0
dla
0
2
<
=
ω
ω
ϕ
o
( )
s
/
rad
1
dla
90
2
>
−
=
ω
ω
ϕ
o
( )
ω
ϕ
2
jest sieczną przechodzącą przez punkty o współrzędnych
(
)
0
,
01
.
0
=
=
ϕ
ω
i
(
)
o
90
,
1
−
=
=
ϕ
ω
dla
1
01
.
0
s
≤
≤
ω
ω
( )
s
/
rad
1
dla
dB
0
L
3
<
=
ω
ω
( )
s
/
rad
1
dla
dB
log
20
L
3
>
−
=
ω
ω
ω
( )
s
/
rad
1
.
0
dla
0
3
<
=
ω
ω
ϕ
o
( )
s
/
rad
10
dla
90
3
>
−
=
ω
ω
ϕ
o
( )
ω
ϕ
3
jest sieczną przechodzącą przez punkty o współrzędnych
(
)
0
,
1
.
0
=
=
ϕ
ω
i
(
)
o
90
,
10
−
=
=
ϕ
ω
dla
10
1
.
0
≤
≤
ω
( )
s
/
rad
1
.
0
dla
dB
0
L
4
<
=
ω
ω
( )
s
/
rad
1
.
0
dla
dB
1
.
0
log
20
L
4
>
−
=
ω
ω
ω
( )
s
/
rad
01
.
0
dla
0
4
<
=
ω
ω
ϕ
o
( )
s
/
rad
1
dla
90
4
>
−
=
ω
ω
ϕ
o
( )
ω
ϕ
4
jest sieczną przechodzącą przez punkty o współrzędnych
(
)
0
,
01
.
0
=
=
ϕ
ω
i
(
)
o
90
,
1
−
=
=
ϕ
ω
dla
1
01
.
0
≤
≤
ω
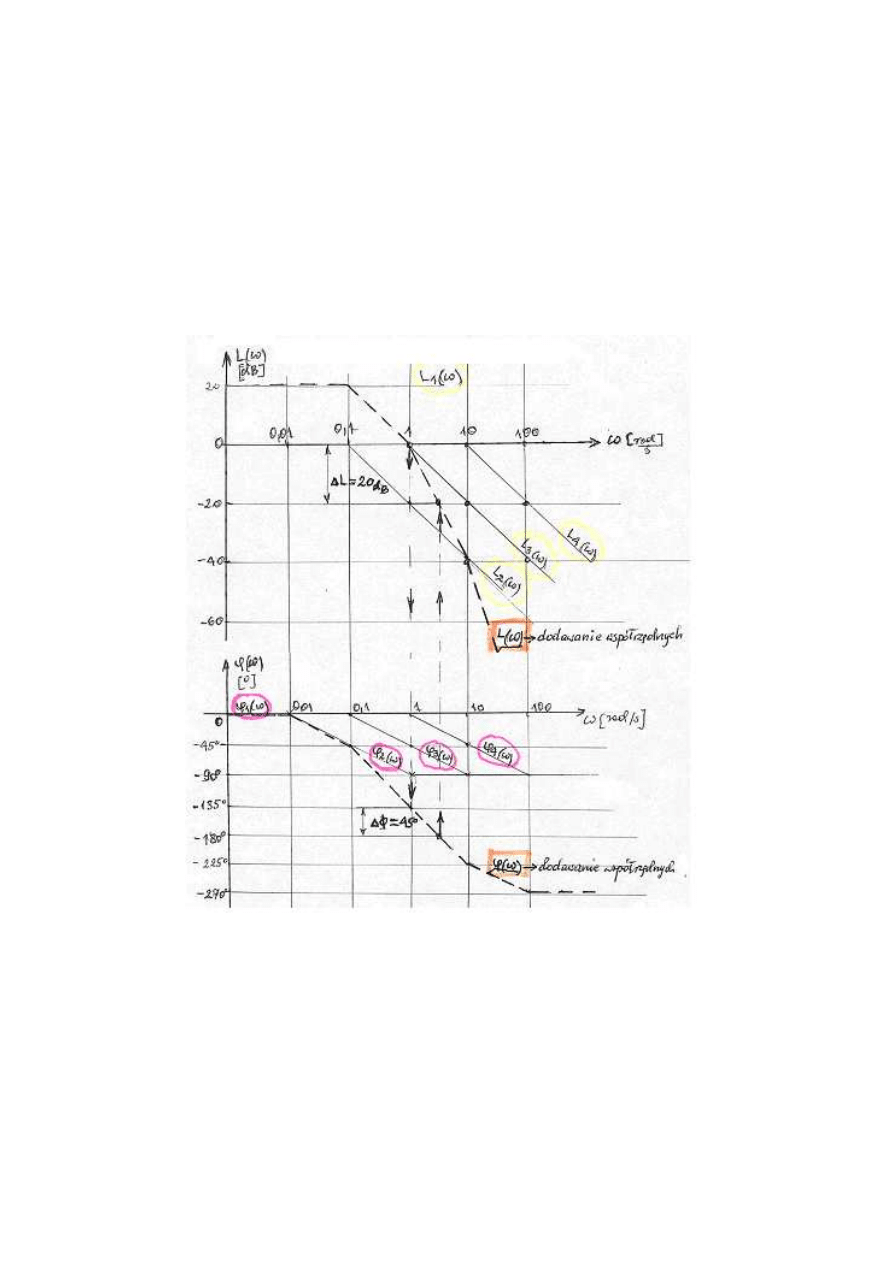
Rys.4. Zapas modułu i zapas fazy układu zamkniętego wyznaczony z
logarytmicznego kryterium Nyquista.
Z wykresów charakterystyk logarytmicznych amplitudowej i fazowej
wynika, że układ po zamknięciu będzie stabilny z zapasem modułu
dB
20
L
=
∆
i zapasu fazy
o
45
=
φ
∆
.
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 5 pow
Ćwiczenie 5 pow
Ćwiczenie 4 pow
Ćwiczenie 2 pow
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
więcej podobnych podstron