Ćwiczenie 2
Temat: Ocena jakości regulacji układów automatyki. Wyznaczanie
uchybu. Analiza układów automatyki z korekcją.
Przykład 1
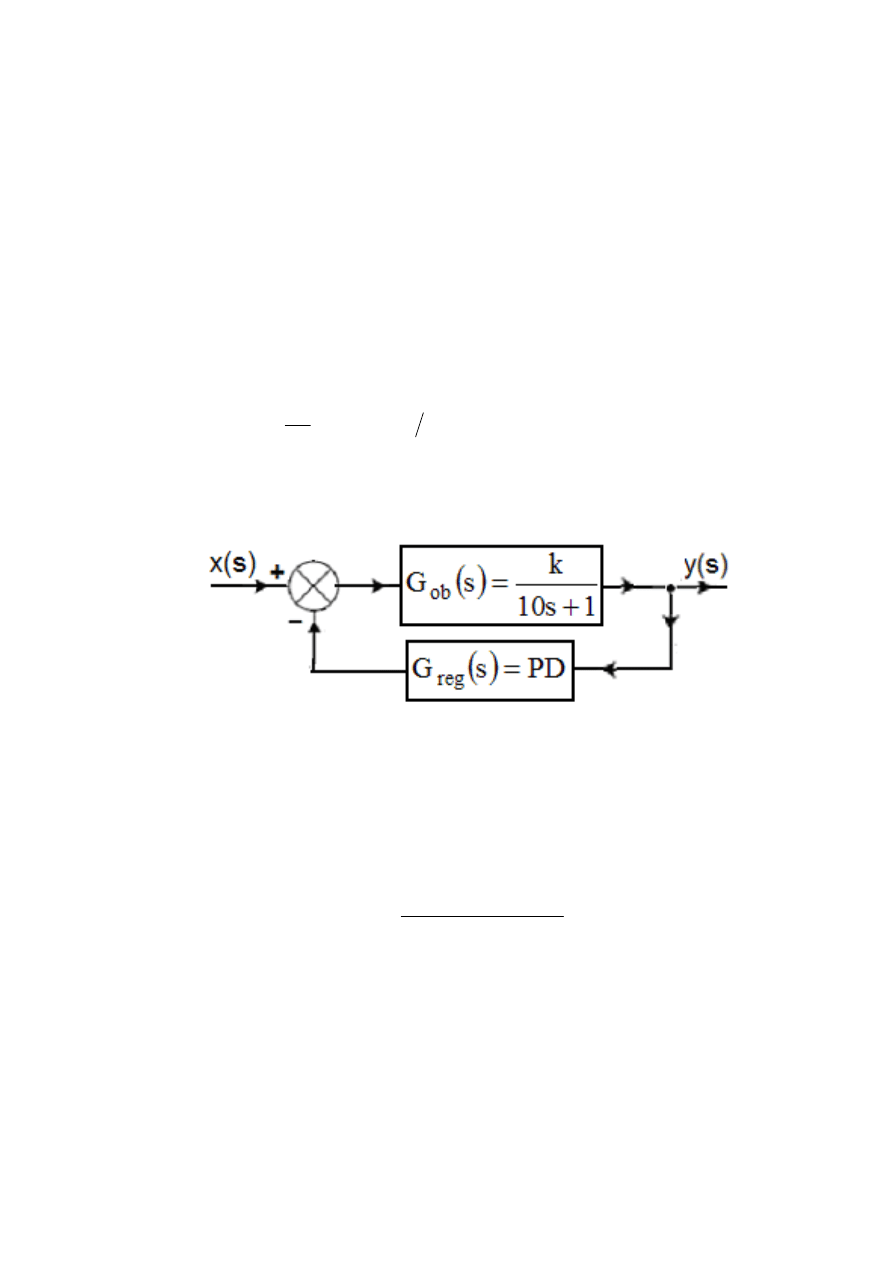
Dla układu automatyki jak na rysunku 1,
wyznaczyć kąt
przesunięcia fazowego
ϕ
między odpowiedzią a wymuszeniem dla
[ ]
s
1
.
0
T
D
=
,
k
10
k
p
=
,
[ ]
s
1
10
=
ω
.
Schemat układu automatyki złożonego z obiektu i regulatora
Rys.1. Schemat układu automatyki
R o z w i ą z a n i e
Transmitancja zastępcza układu automatyki jest
( )
( )
( )
( )
s
G
s
G
1
s
G
s
G
reg
ob
ob
z
+
=
,
Transmitancja regulatora PD
( )
(
)
s
T
1
k
s
G
D
p
reg
+
=
,
Zatem

( )
(
)
(
)
p
D
p
D
p
z
kk
T
10
s
kk
1
k
s
T
1
k
1
Ts
k
1
1
Ts
k
s
G
+
+
+
=
+
⋅
+
+
+
=
,
Podstawiając dane otrzymamy
( )
1
s
k
s
G
1
z
+
=
,
11
k
k
1
=
.
Aby wyznaczyć kąt przesunięcia fazowego
ϕ
przy zadanych
parametrach, należy przejść z transmitancji operatorowej na
widmową, zatem
( )
(
)
(
)(
)
(
) (
)
2
1
2
1
1
z
1
k
j
1
k
j
1
j
1
j
1
k
j
G
ω
ω
ω
ω
ω
ω
ω
+
−
+
=
−
+
−
=
,
Część rzeczywista i urojona transmitancji widmowej
( )
(
)
2
1
1
k
P
ω
ω
+
=
,
( )
(
)
2
1
1
k
Q
ω
ω
ω
+
−
=
.
Stąd kąt wyprzedzenia fazowego wyznaczymy ze wzoru
( )
( )
'
11
24
10
P
Q
tan
o
−
=
→
−
=
−
=
=
ϕ
ω
ω
ω
ϕ
.
Przykład 2
Wyznaczyć odchyłkę statyczną (uchyb
( )
t
e
st
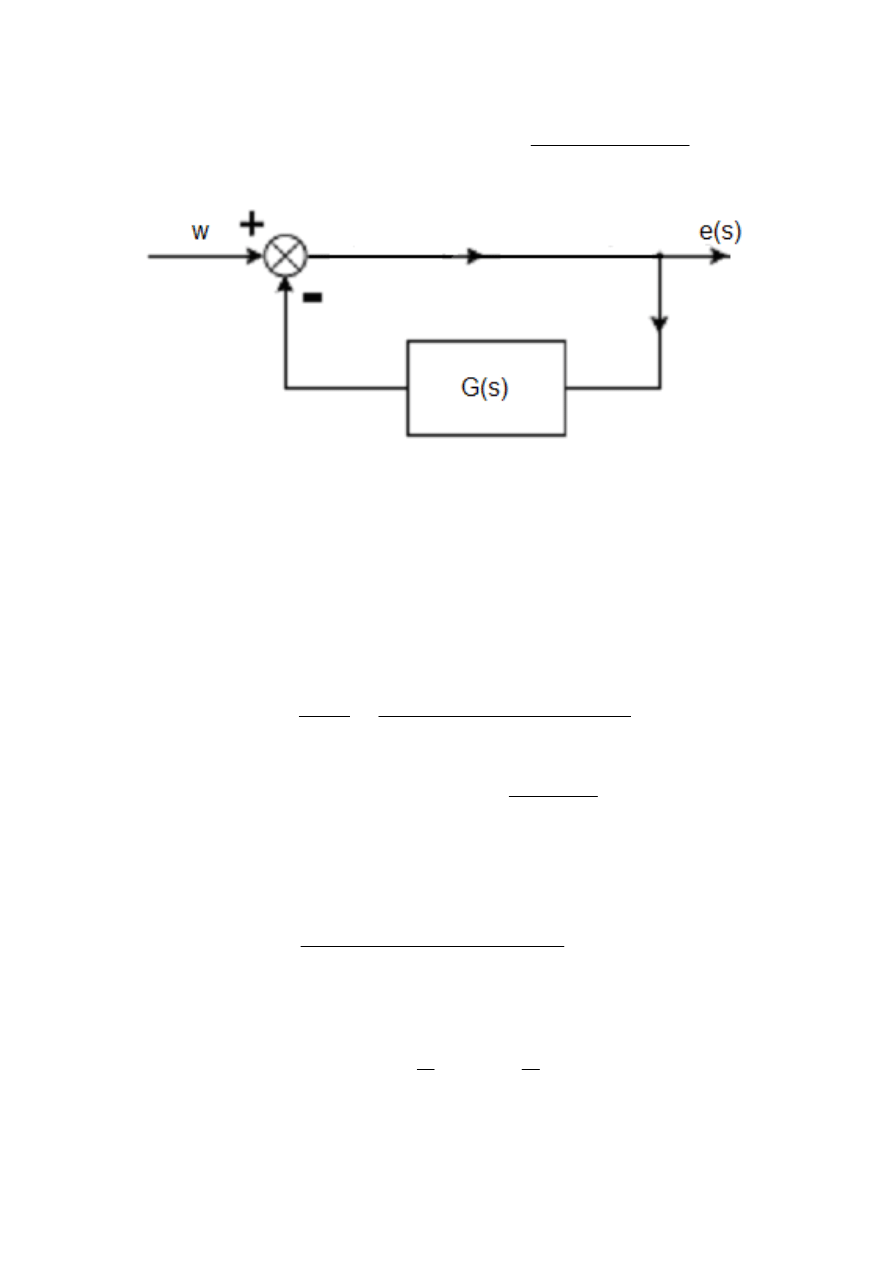
) układu którego schemat
blokowy (strukturalny) przedstawia rysunek 2 przy założeniu
zerowych warunków początkowych dla danych:
10
t
5
t
2
w
2
+
+
=
,
( )
(
)
(
)
2
s
1
s
02
.
0
1
s
15
.
0
50
s
G
+
+
=
Rys.2. Schemat strukturalny badanego układu automatyki
R o z w i ą z a n i e
Transmitancja zastępcza badanego układu automatyki jest
( ) ( )
( )
( )
( ) ( )
( )
( )
s
G
1
s
w
s
w
s
G
s
e
,
50
s
5
.
7
s
s
02
.
0
s
s
02
.
0
s
w
s
e
s
G
z
2
3
2
3
z
+
=
=
→
+
+
+
+
=
=
Dokonujemy rozkładu transmitancji
( )
s
G
z
w szereg potęgowy, a więc
( )
....
s
C
6
1
s
C
2
1
s
C
C
50
s
5
.
7
s
s
02
.
0
s
s
02
.
0
s
G
3
3
2
2
1
0
2
3
2
3
z
+
+
+
+
=
=
+
+
+
+
=
stąd

( )
( )
s
w
....
s
C
6
1
s
C
2
1
s
C
C
s
e
3
3
2
2
1
0
st
+
+
+
+
=
Po poddaniu powyższego równania odwrotnemu przekształceniu
Laplace’a otrzymamy wzór na odpowiedź w stanie ustalonym, a więc
( )
( )
( )
( )
( )
...
dt
t
w
d
C
6
1
dt
t
w
d
C
2
1
dt
t
dw
C
t
w
C
t
e
3
3
3
2
2
2
1
0
st
+
+
+
+
=
gdzie
( )
0
s
0
s
G
C
=
↓
=
=0,
( )
(
)(
) (
)(
)
(
)
0
50
s
5
.
7
s
s
02
.
0
s
s
02
.
0
5
.
7
s
2
s
06
.
0
50
s
5
.
7
s
s
02
.
0
s
2
s
06
.
0
ds
s
dG
C
2
2
3
2
3
2
2
3
2
0
s
1
=
+
+
+
+
+
+
−
+
+
+
+
=
=
=
=
↓
( )
04
.
0
ds
dC
ds
s
G
d
C
0
s
1
0
s
2
2
2
=
=
=
=
↓
=
↓
,
( )
0
s
2
0
s
3
3
3
ds
dC
ds
s
G
d
C
=
↓
=
↓
=
=
,
( )
5
t
4
dt
t
dw
+
=
,
( )
,
4
dt
t
w
d
2
2
=
( )
0
dt
t
w
d
3
3
=
Po podstawieniu poszczególnych składników do powyższego
równania otrzymamy
( )
08
.
0
t
e
st
=
lub
( )
( ) ( )
( )
( )
[ ]
( ) ( )
[
]
s
w
s
G
L
s
e
L
t
e
s
w
s
G
t
e
z
1
1
z
−
−
=
=
→
=
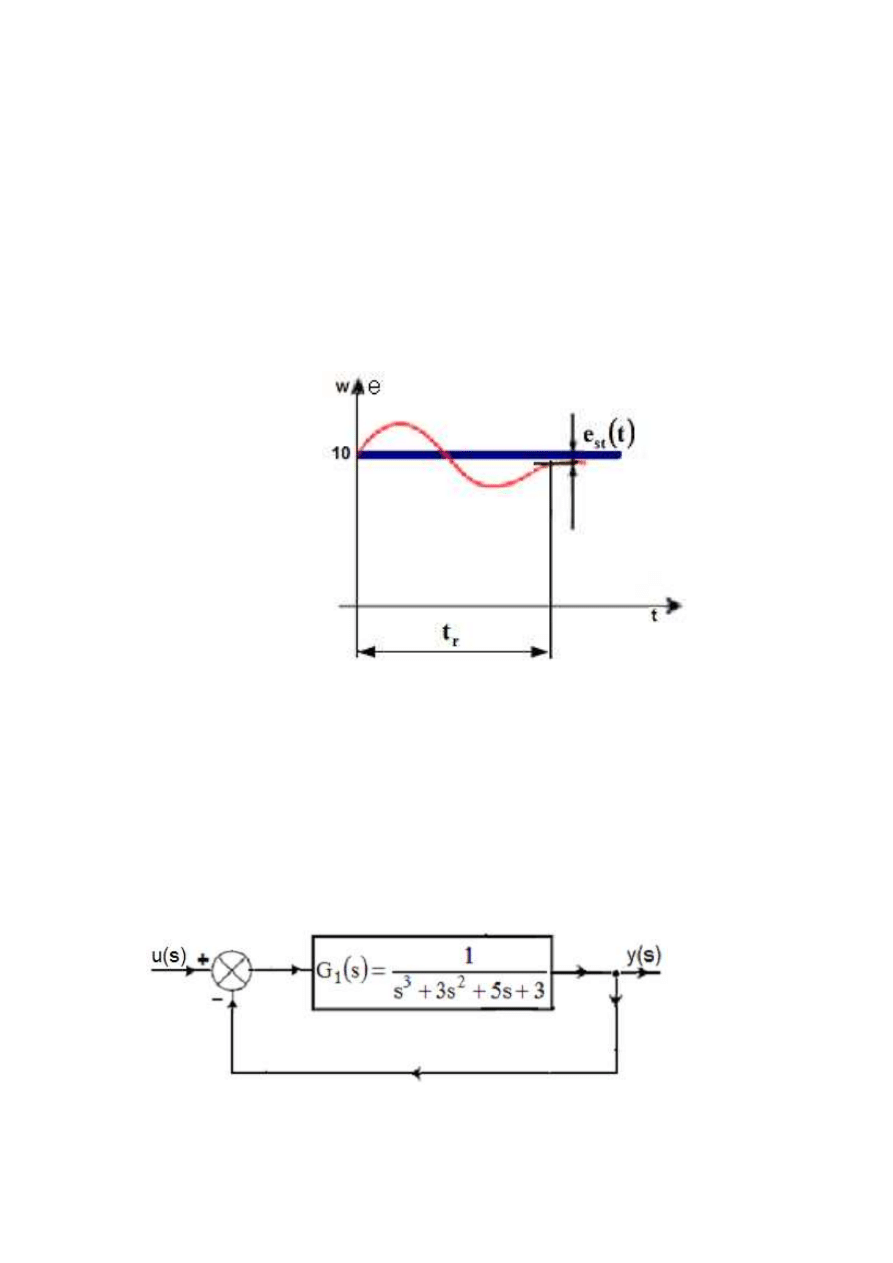
Rys.3. Wykres zmiany odchyłki statycznej
Przykład 3
Zbadać
stabilność
układu
automatyki
którego
schemat
przedstawia rysunek 4
korzystając z ogólnego warunku stabilności
oraz z kryteriów Hurwitza i Nyquista. Określić zapas modułu.
Rys.4. Schemat układu automatyki
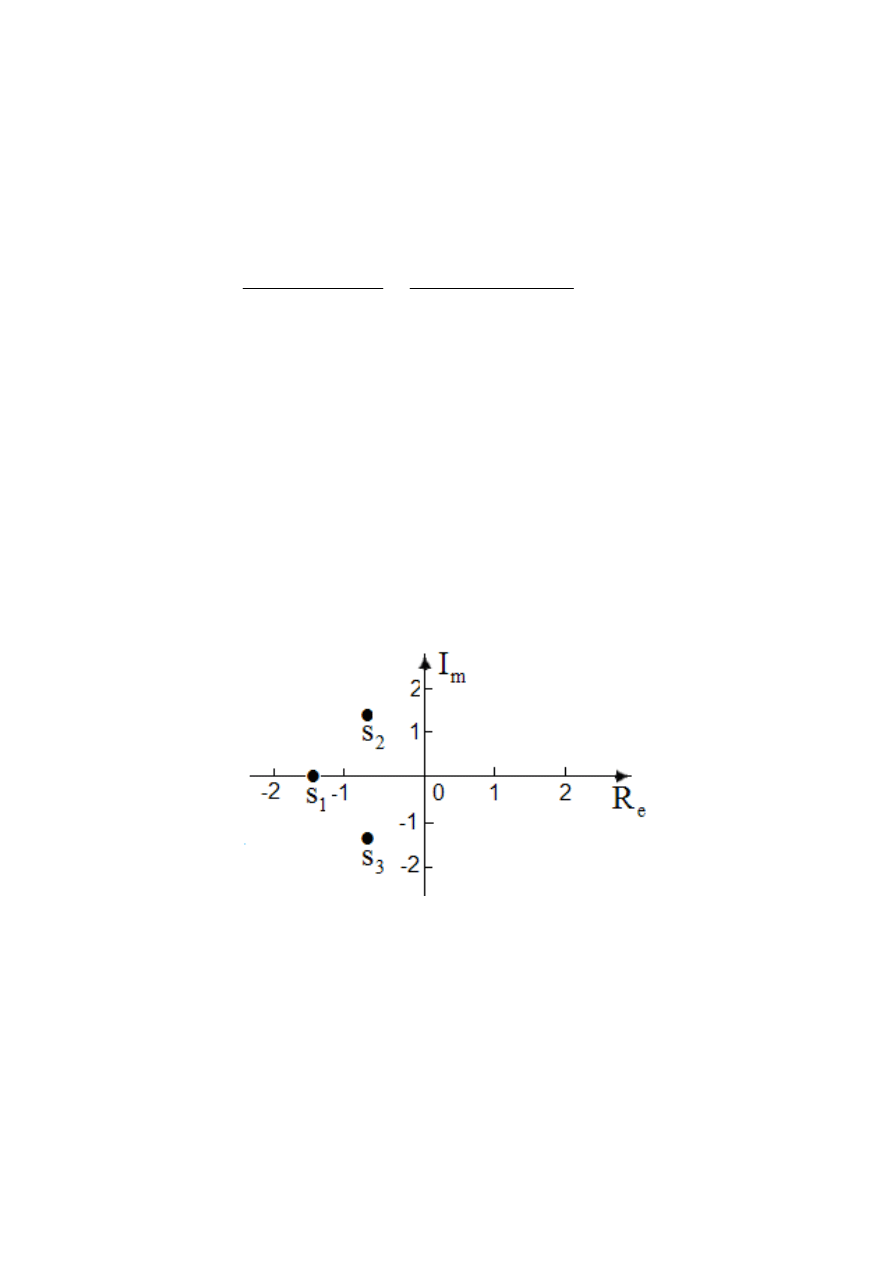
R o z w i ą z a n i e
a) Kryterium ogólne dla układu zamkniętego
Transmitancja zastępcza zamkniętego układu automatyki jest
( )
( )
( ) ( )
4
s
5
s
3
s
1
s
G
s
G
1
s
G
s
G
2
3
2
1
1
z
+
+
+
=
+
=
,
( )
1
s
G
2
=
.
Pierwiastki równania charakterystycznego są
,
46
.
1
i
77
.
0
s
,
46
.
1
i
77
.
0
s
s
,
45
.
1
s
0
4
s
5
s
3
s
3
3
2
1
2
3
⋅
−
−
=
⋅
+
−
=
=
−
=
→
=
+
+
+
Kryterium ogólne jest spełnione, ponieważ wszystkie części
rzeczywiste pierwiastków Hurwitza są spełnione i leżą w lewej
półpłaszczyźnie liczb zespolonych.
Rys.5. Rozkład pierwiastków równania charakterystycznego
b) Kryterium Hurwitza dla układu zamkniętego
Kryterium koniecznym Hurwitza jest, aby wszystkie współczynniki
równania charakterystycznego były większe od zera, zatem
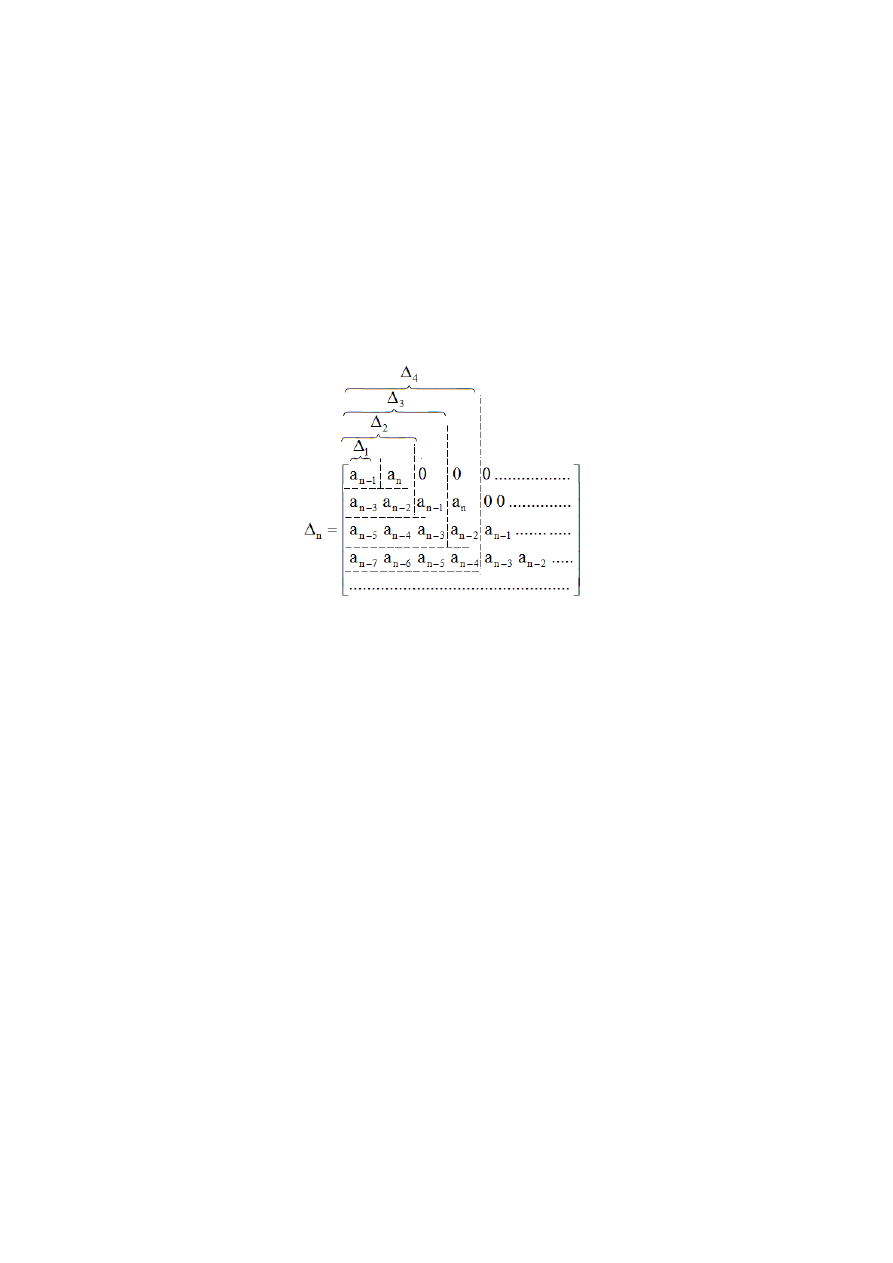
.
1
a
,
3
a
,
5
a
,
4
a
3
2
1
0
=
=
=
=
Jak widać kryterium to jest spełnione (
0
a
i
>
)
Kryterium dostatecznym Hurwitza jest, aby wszystkie
podwyznaczniki utworzone z wyznacznika głównego były większe
od zera, tj.
Wyznacznik główny
,
[ ] [ ]
,
0
44
4
0
0
3
5
4
0
1
3
a
0
0
a
a
a
0
a
a
,
0
11
5
4
1
3
a
a
a
a
,
0
3
a
0
2
1
0
3
2
3
1
0
3
2
2
2
1
>
=
=
=
>
=
=
=
>
=
=
∆
∆
∆
lub
44
11
4
a
a
2
0
3
1
n
0
n
=
⋅
=
=
→
=
−
∆
∆
∆
∆
.
Według obydwu kryteriów Hurwitza układ zamknięty jest stabilny
c) Kryterium Nyquista dla układu otwartego
Według kryterium Nyquista, charakterystyka amplitudowo-
fazowa układu otwartego nie może obejmować punktu o
współrzędnych (-1,j0).
Należy, więc określić transmitancję operatorową
( )
s
G
o
układu
otwartego i przejść do transmitancji widmowej
( )
ω
j
G
o
wydzielając
część rzeczywistą
( )
ω
P
i urojoną
( )
ω
Q
.
( )
=
s
G
o
3
s
5
s
3
s
1
2
3
+
+
+
,
( )
( )
( )
( )
(
) (
)
(
) (
)
(
) (
)
[
]
(
) (
)
[
]
(
) (
)
(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
o
5
1
9
5
j
1
3
5
j
1
3
5
j
1
3
5
j
1
3
5
j
1
3
1
3
j
5
j
3
j
1
j
G
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
+
−
−
−
−
=
=
−
−
−
−
+
−
−
−
−
=
=
−
+
−
=
+
+
+
=
( )
(
)
(
)
(
)
2
2
2
2
2
2
5
1
9
1
3
P
ω
ω
ω
ω
ω
−
+
−
−
=
,
( )
(
)
(
)
(
)
2
2
2
2
2
2
5
1
9
5
Q
ω
ω
ω
ω
ω
ω
−
+
−
−
−
=
.
( )
(
)
[ ]
s
1
5
,
0
0
5
0
Q
2
1
2
=
=
→
=
−
→
=
ω
ω
ω
ω
ω
.
(
)
12
1
5
P
−
=
=
ω
,
( )
92
.
0
08
.
0
1
P
1
M
=
−
=
−
=
−
π
ω
∆
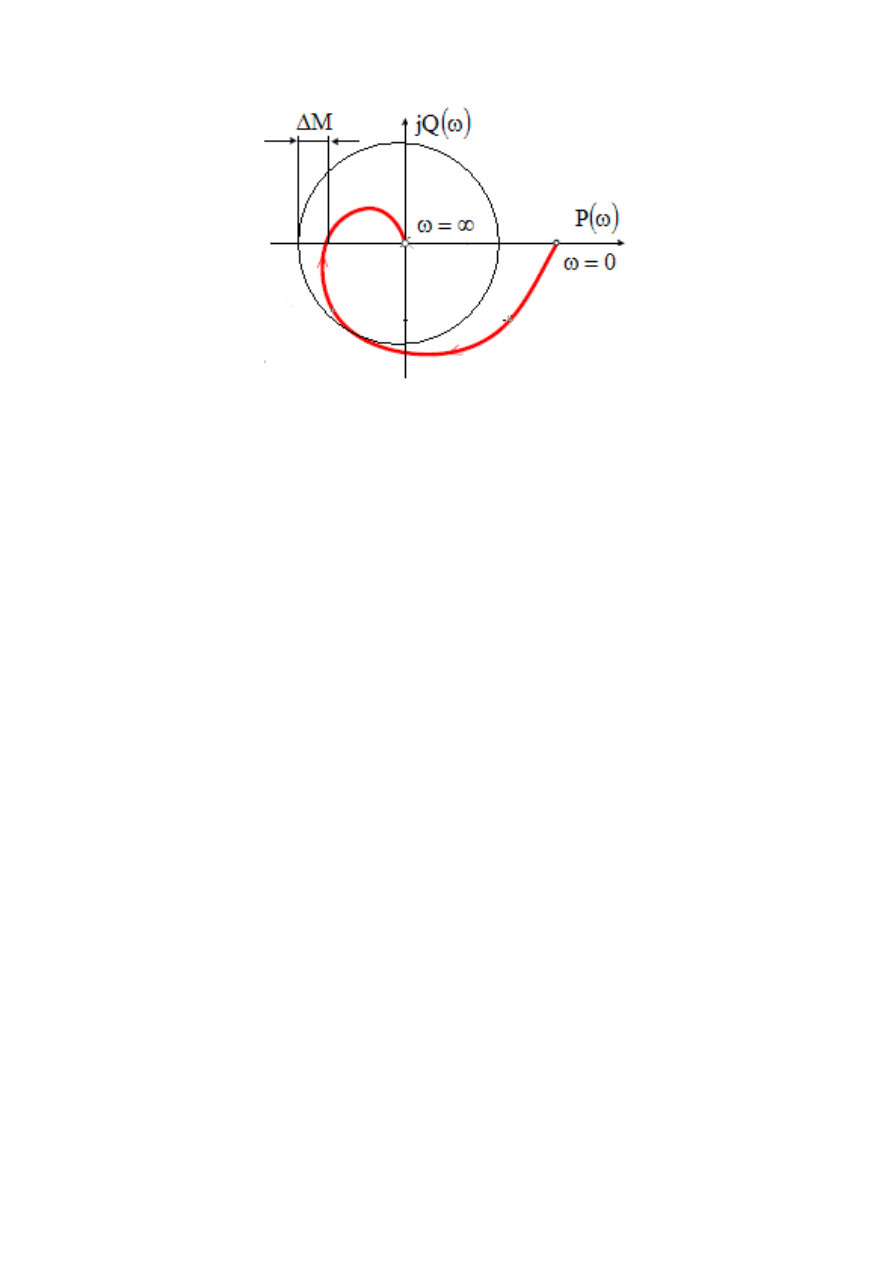
Rys.6. Charakterystyka amplitudowo-fazowa układu automatyki
Według obydwu kryteriów Hurwitza dla układu otwartego jest
Równanie charakterystyczne
3
s
5
s
3
s
2
3
+
+
+
,
.
1
a
,
3
a
,
5
a
,
3
a
3
2
1
0
=
=
=
=
0
a
i
>
.
[ ] [ ]
,
0
36
3
0
0
3
5
3
0
1
3
a
0
0
a
a
a
0
a
a
,
0
12
5
3
1
3
a
a
a
a
,
0
3
a
0
2
1
0
3
2
3
1
0
3
2
2
2
1
>
=
=
=
>
=
=
=
>
=
=
∆
∆
∆
lub
36
12
3
a
a
2
0
3
1
n
0
n
=
⋅
=
=
→
=
−
∆
∆
∆
∆
.
Oba kryteria Hurwitza są również spełnione, a więc układ automatyki
jest stabilny.
Przykład 4
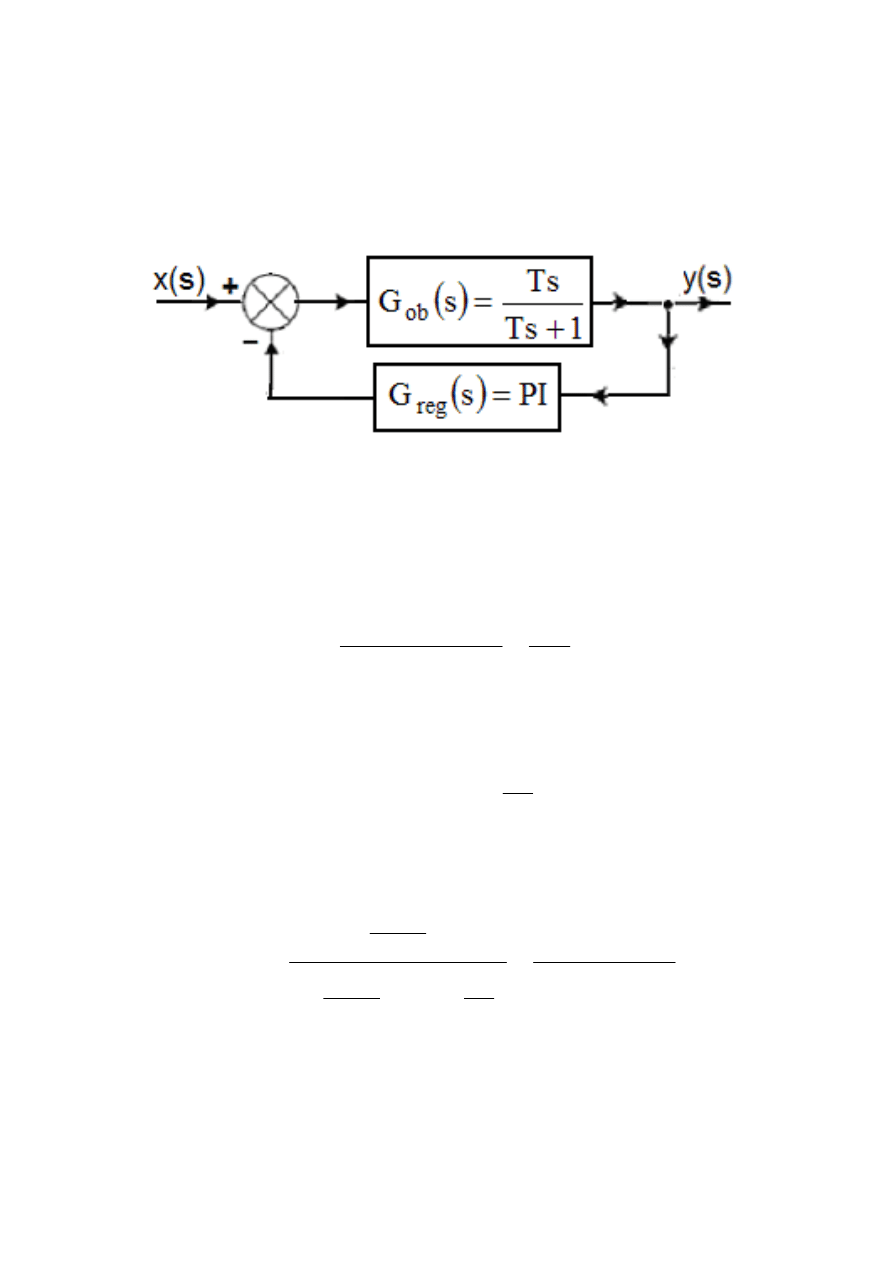
Na podanym na rysunku 7
układzie automatyki w rezonansie stosunek
sygnału wejściowego do wyjściowego wynosi 5. Przy
T
T
i
=
określić
wzmocnienie regulatora PI oraz dla
o
45
−
=
ϕ
wyznaczyć częstość.
Rys.7. Schemat układu automatyki
R o z w i ą z a n i e
Transmitancja zastępcza układu automatyki jest
( )
( )
( )
( )
( )
( )
2
.
0
s
x
s
y
s
G
s
G
1
s
G
s
G
reg
ob
ob
z
=
=
+
=
,
Transmitancja regulatora PI
( )
+
=
s
T
1
1
k
s
G
i
p
reg
,
Zatem
( )
(
)
(
)
p
i
p
z
k
1
1
Ts
Ts
s
T
1
1
k
1
Ts
Ts
1
1
Ts
Ts
s
G
+
+
=
+
⋅
+
+
+
=
,
Dla rezonansu
Ts
1
Ts
,
1
Ts
≅
+
→
>>
,
Czyli współczynnik wzmocnienia regulatora
p
k jest
( )
4
k
2
.
0
k
1
1
s
G
p
p
z
=
→
=
+
=
.
Aby wyznaczyć częstość, należy przejść z transmitancji operatorowej
na widmową, zatem
( )
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
.
T
1
k
1
jT
T
1
k
1
T
1
T
j
T
k
1
T
1
jT
1
jT
1
jT
j
k
1
T
j
G
2
2
p
2
2
p
2
2
2
2
p
p
z
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
+
+
+
=
=
+
+
+
=
−
−
⋅
+
+
=
,
Część rzeczywista i urojona transmitancji widmowej
( )
(
)
(
)
1
T
k
1
T
P
2
2
p
2
2
+
+
=
ω
ω
ω
,
( )
(
)
(
)
1
T
k
1
T
Q
2
2
p
+
+
=
ω
ω
ω
.
Częstość wyznaczamy ze wzoru
( )
( )
T
1
1
45
tan
T
1
P
Q
tan
=
→
=
=
=
=
ω
ω
ω
ω
ϕ
o
.
Przykład 5
Dla częstości
[ ]
s
1
7
=
ω
i opóźnienia fazowego
o
35
−
=
ϕ
dobrać
czas wyprzedzenia regulatora
D
T
i stałą czasową
T
obiektu, tak aby
D
T
T
=
. Schemat układu automatyki złożonego z obiektu i regulatora
przedstawia rysunek 8.
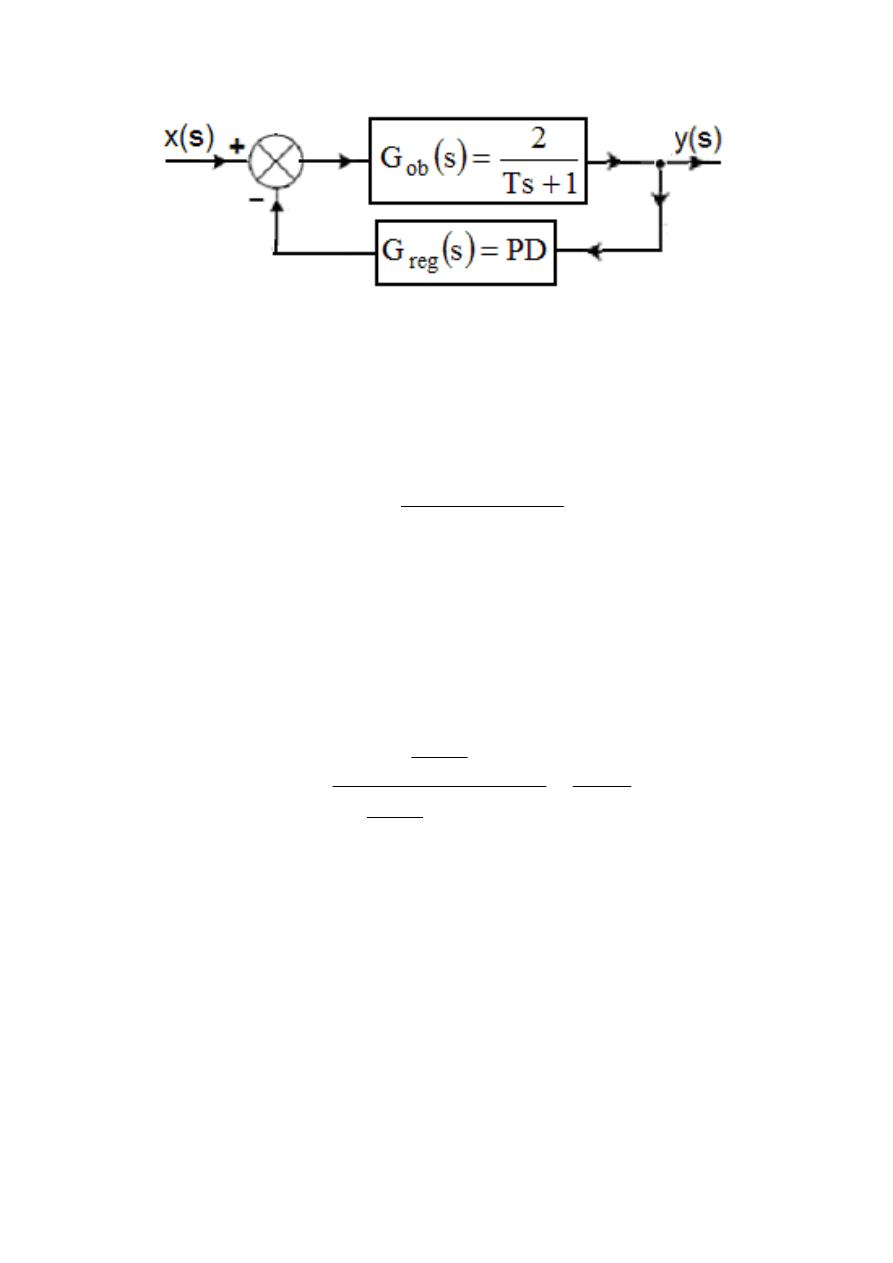
Rys.8. Schemat układu automatyki
R o z w i ą z a n i e
Transmitancja zastępcza układu automatyki jest
( )
( )
( )
( )
s
G
s
G
1
s
G
s
G
reg
ob
ob
z
+
=
,
Transmitancja regulatora PD
( )
(
)
s
T
1
k
s
G
D
p
reg
+
=
,
Zatem
( )
(
)
b
as
2
s
T
1
k
1
Ts
2
1
1
Ts
2
s
G
D
p
z
+
=
+
⋅
+
+
+
=
,
gdzie
D
p
T
k
2
T
a
+
=
,
p
k
2
1
b
+
=
.
Aby wyznaczyć czas wyprzedzenia regulatora i stałą czasową obiektu
przy zadanych parametrach, należy przejść z transmitancji
operatorowej na widmową, zatem

( )
(
)
(
)(
)
(
) (
) (
)
2
2
2
2
2
2
2
2
2
z
a
b
a
2
j
a
b
b
2
a
b
a
2
j
b
2
aj
b
aj
b
aj
b
2
j
G
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
+
=
+
−
=
−
+
−
=
,
Część rzeczywista i urojona transmitancji widmowej
( )
(
)
2
2
2
a
b
b
2
P
ω
ω
+
=
,
( )
(
)
2
2
2
a
b
a
2
Q
ω
ω
ω
+
−
=
.
Czas wyprzedzenia regulatora
D
T i stałą czasową T obiektu
wyznaczymy ze wzoru
( )
( )
(
)
p
D
p
k
2
1
T
k
2
T
b
a
P
Q
7
.
0
35
tan
tan
+
+
−
=
−
=
=
−
=
−
=
ω
ω
ω
ω
ϕ
o
,
Przy nastawie
D
T
T
=
otrzymamy
[ ]
s
1
.
0
7
7
.
0
7
.
0
T
T
7
.
0
=
=
=
→
=
ω
ω
Tak więc, aby były spełnione wartości parametrów
ω
ϕ
i
, muszą
być
[ ]
s
1
.
0
T
T
D
=
=
.
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 3 pow
Ćwiczenie 5 pow
Ćwiczenie 5 pow
Ćwiczenie 4 pow
Ćwiczenie 3 pow
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
więcej podobnych podstron