EFEKT SUBSTYTUCYJNY

I EFEKT DOCHODOWY

• Jak konsument wybierający koszyk reaguje na

zmianę ceny jednego z dóbr?

• Kiedy cena zmienia się można zauważyć dwa

efekty:

– Zmienia się stosunek wg. którego wymieniane są

dobra

– Zmienia się ogólna siła nabywcza dochodu

• Te dwa efekty nazwiemy:

– Efektem substytucyjnym
– Efektem dochodowym

• Ruch cen zostaje więc rozbity na dwa etapy

– Zmiana ceny i takie dostosowanie dochodu aby siła

nabywcza

pozostała nie zmieniona

– Dostosowanie siły nabywczej przy niezmienionych

cenach

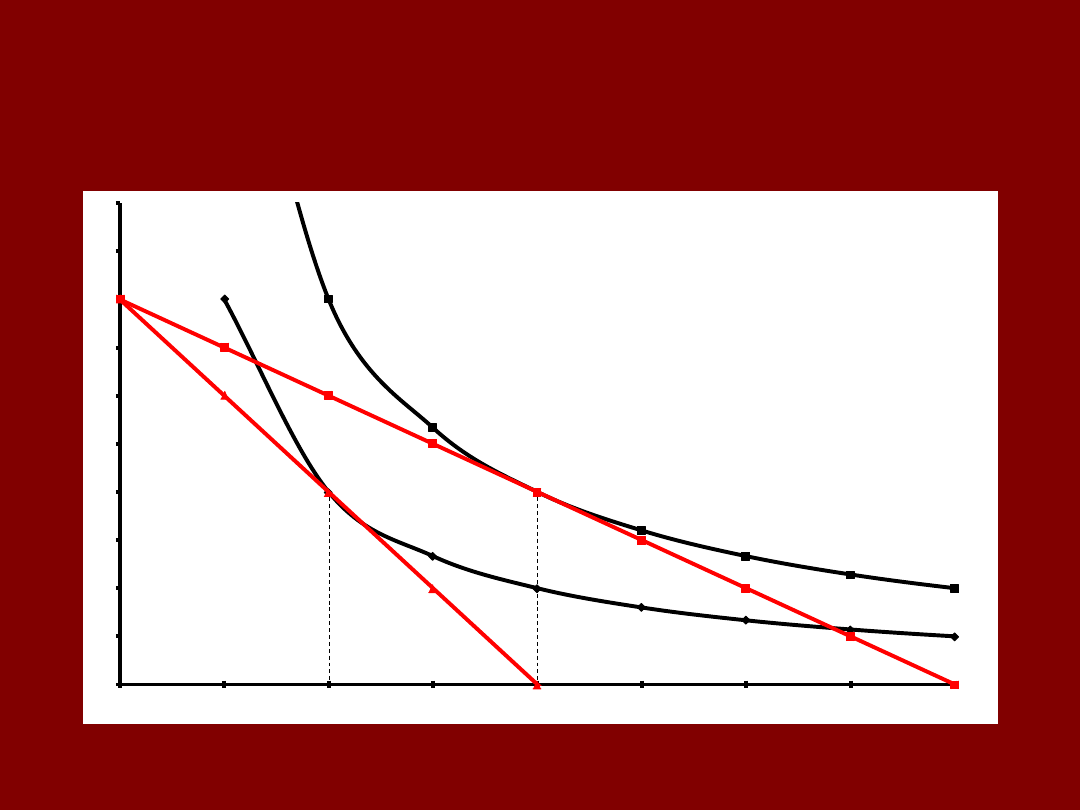
Zmiana popytu na dobro X

na skutek zmniejszenia ceny dobra X

(cena dobra Y oraz dochód M są stałe)

IL

O

ŚĆ

Y

ILOŚĆ X

A

B

X

1

X

3

(x

1

, y

1

)

• Zmianę popytu na dobro X na skutek

zmniejszenia

się ceny dobra X rozbijemy

na dwa etapy:

– Obrót

• Nachylenie linii budżetu zmienia się
• Siła nabywcza dochodu pozostaje taka

sama

– Przesunięcie

• Nachylenie linii budżetu pozostaje stałe
• Zmienia się siła nabywcza dochodu

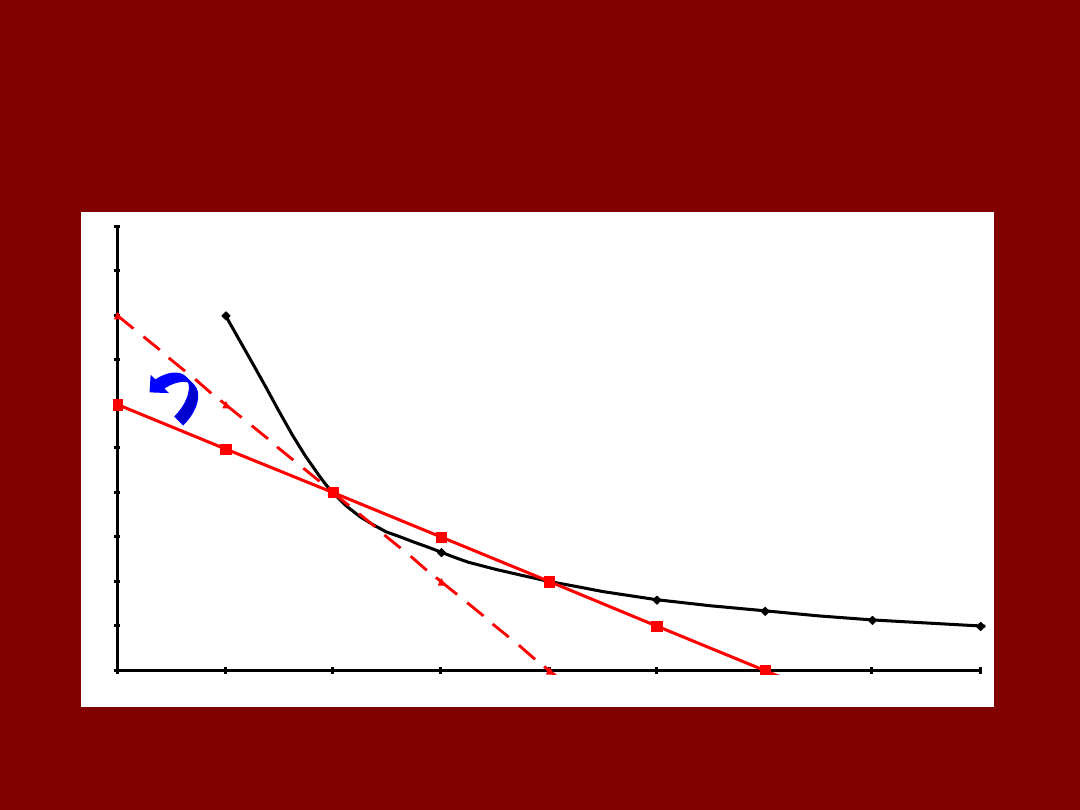
OBRÓT

ILOŚĆ X

IL

O

Ś

Ć

Y

A

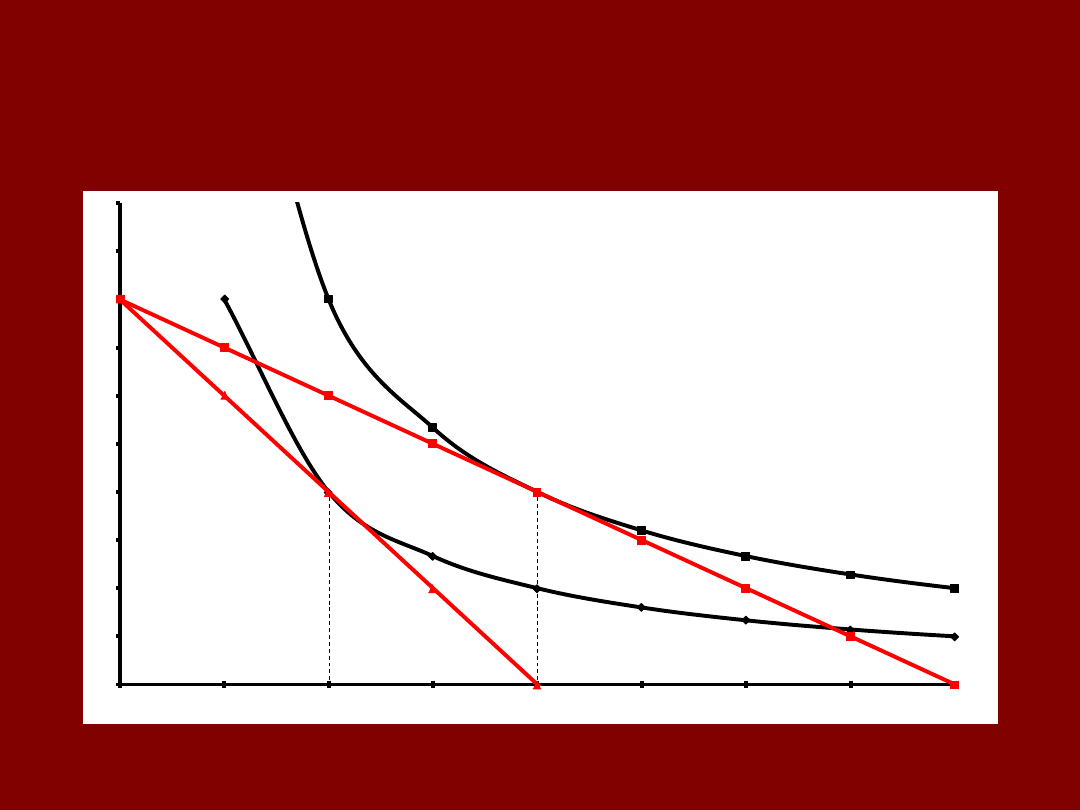
Zmiana popytu na dobro X

na skutek zmniejszenia ceny dobra X

(cena dobra Y oraz dochód M są stałe)

IL

O

ŚĆ

Y

ILOŚĆ X

A

B

X

1

X

3

(x

1

, y

1

)

• Koszyk A (x

1

,y

1

)

leży na obróconej linii

budżetowej – jaki zatem musi być poziom
dochodu aby koszyk A nadal

był dostępny?

• M’ – dochód odpowiadający nowej linii

budżetowej

• Koszyk A jest dostępny zarówno przy (p

X1

, p

Y1

,

M) jak i przy (p

X2

, p

Y1

,

M’)

• Zatem:

M’ = p

X2

x

1

+ p

Y1

y

1

M = p

X1

x

1

+ p

Y1

y

1

• M’ – M = p

X2

x

1

+ p

Y1

y

1

- p

X1

x

1

- p

Y1

y

1

• ΔM = x

1

(p

X2

-p

X1

)

• ΔM = x

1

Δp

X

EFEKT SUBSTYTUCYJNY

ILOŚĆ X

IL

O

ŚĆ

Y

A

C

X

1

X2

ΔX

S

ΔX

S

= X

2

(p

X2

,M’) – X

1

(p

X1

,M)

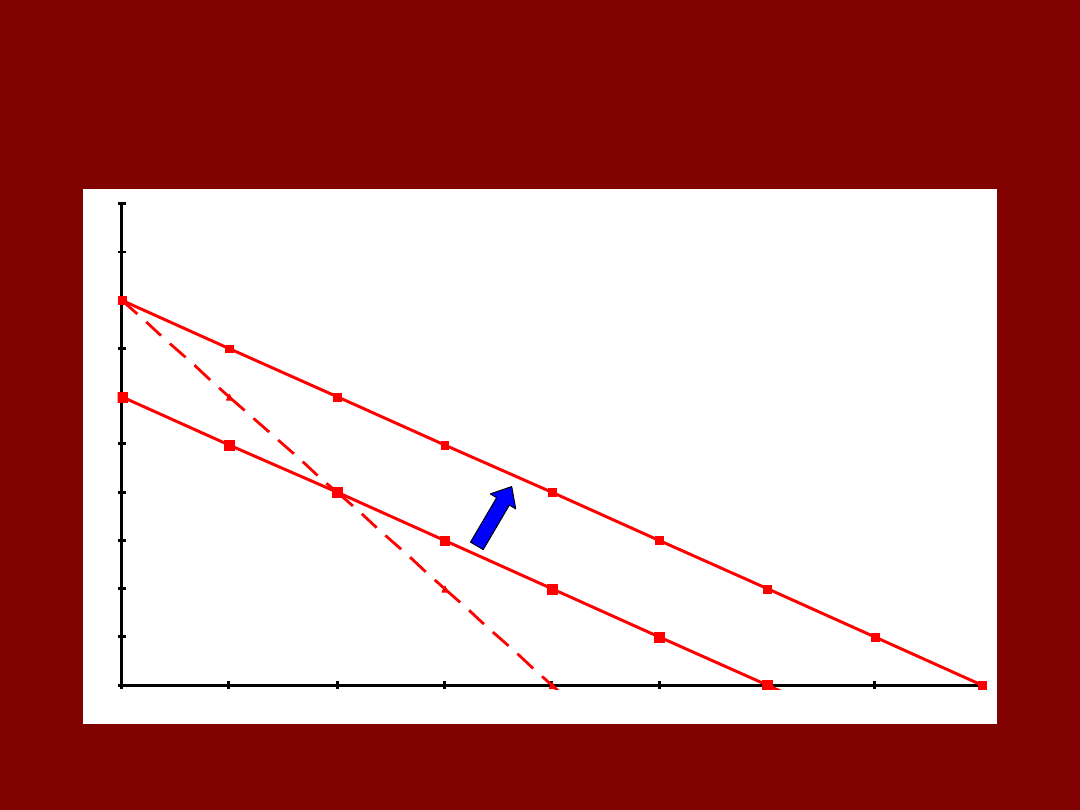
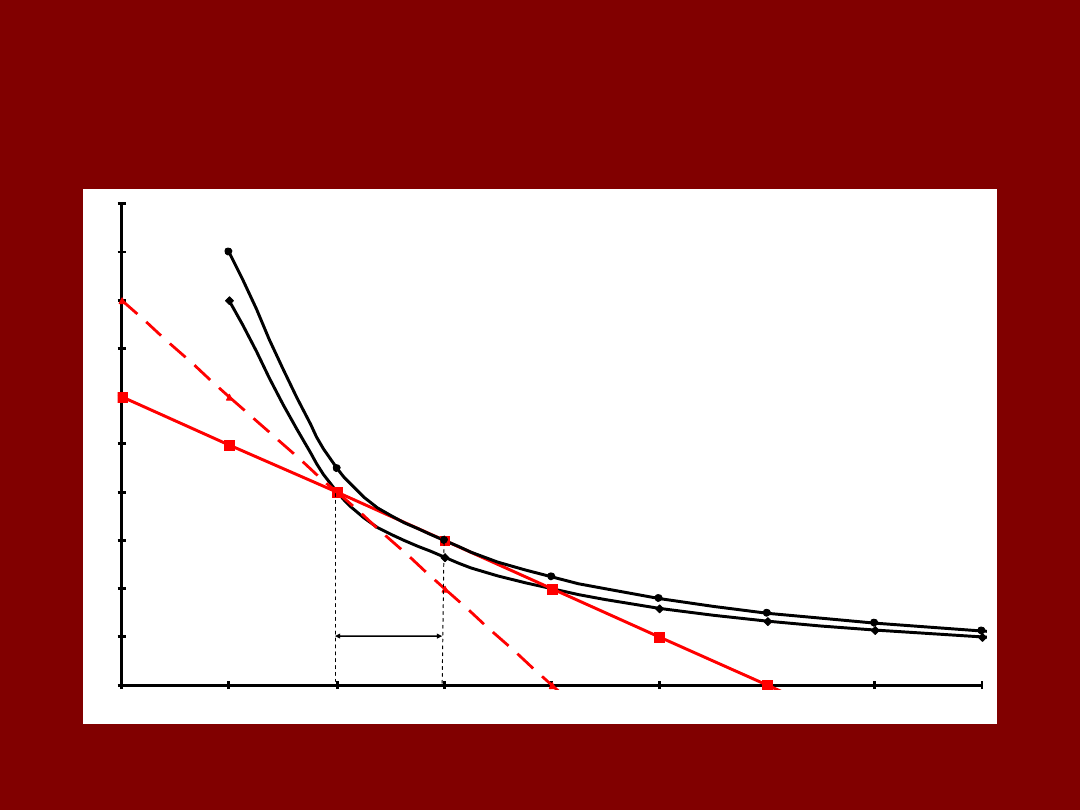
PRZESUNIĘCIE

ILOŚĆ X

IL

O

ŚĆ

Y

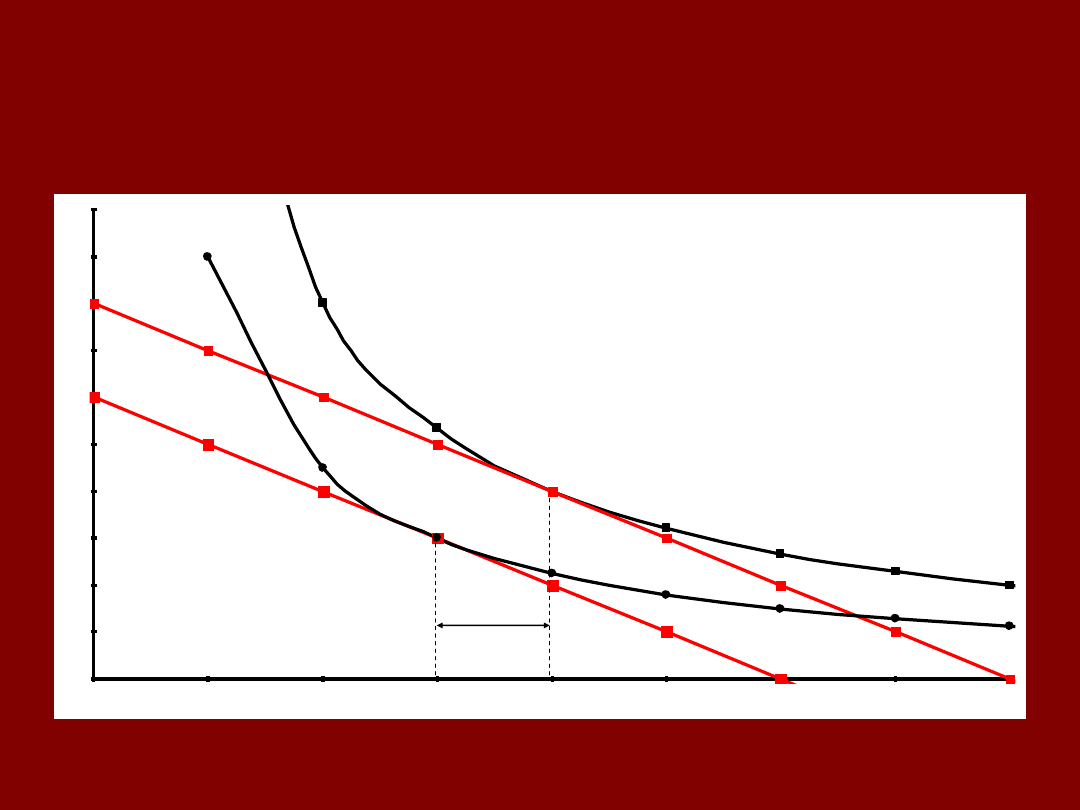
EFEKT DOCHODOWY

ILOŚĆ X

IL

O

Ś

Ć

Y

C

B

X

2

X

3

ΔX

N

ΔX

N

= X

3

(p

X2

,M)

– X

2

(p

X2

,M’)

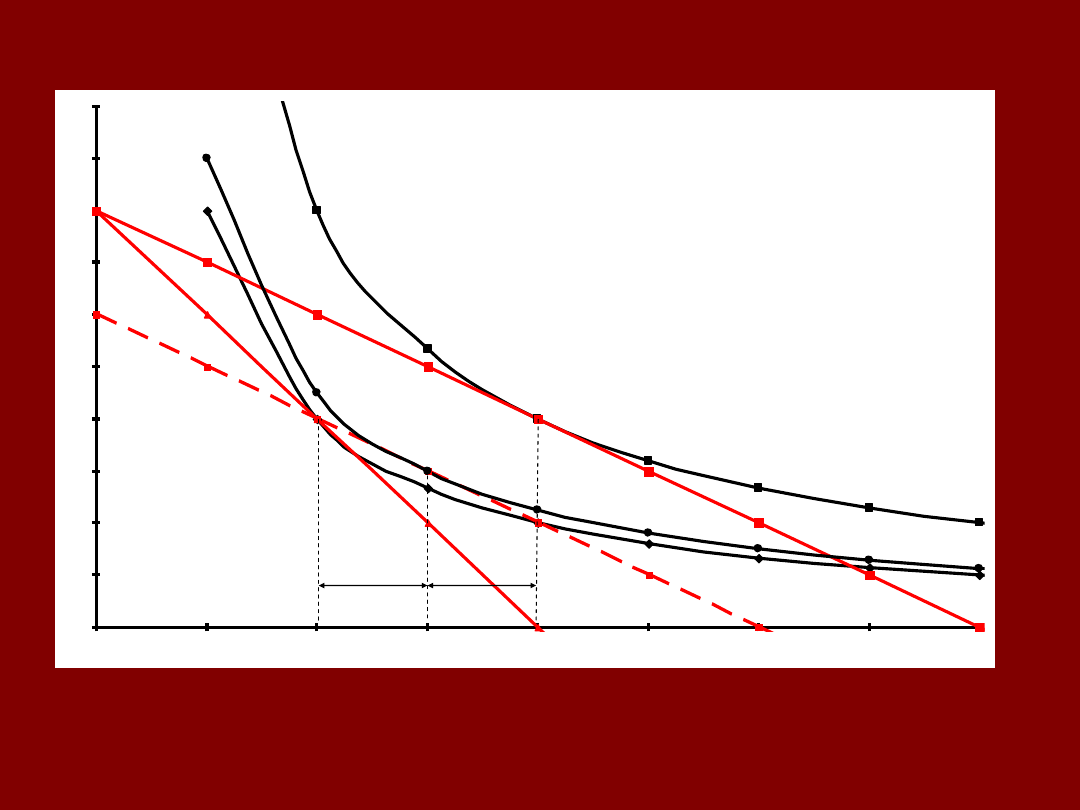
ILOŚĆ X

IL

O

ŚĆ

Y

A

C

B

ΔX

N

ΔX

S

X

1

X

2

X

3

CAŁKOWITA ZMIANA POPYTU

ΔX = ΔX

S

+

ΔX

N

– równanie Słuckiego

X

3

(p

X2

,M) - X

1

(p

X1

,M) =

[X

2

(p

X2

,M’) – X

1

(p

X1

,M)] + [X

3

(p

X2

,M)

– X

2

(p

X2

,M’)]

• Gdy cena wzrasta

– Dobra normalne

ΔX = ΔX

S

+

ΔX

N

(-) = (-) + (-)

– Dobra niższego rzędu

ΔX = ΔX

S

+

ΔX

N

(?) = (-) + (+)

• Dobro Giffena

(+) = (-) + (+)

• Pozostałe dobra niższego rzędu

(-) = (-) + (+)