Obwody RLC przy wymuszeniu sinusoidalnym w stanie ustalonym

opracowała Krystyna Kubas

9

Zastosowana notacja liczb zespolonych

z = a + jb liczba zespolona

z

= a – jb liczba zespolona sprzężona do liczby z

gdzie:

a =

(

)

z

z

+

2

1

b =

(

)

z

z

j

−

2

1

2

2

b

a

z

+

=

moduł liczby zespolonej

arg

z

=arctg

⎟

⎠

⎞

⎜

⎝

⎛

a

b

z

= arctg

∠

⇒

⎟

⎠

⎞

⎜

⎝

⎛

a

b argument liczby zespolonej

Postać algebraiczna liczby zespolonej:

(

)

z

j

z

z

z

∠

+

∠

=

sin

cos

1

9

Zastosowanie liczb zespolonych

Każdy element występujący w obwodzie elektrycznym ma swoją reprezentację w postaci liczby

zespolonej podobną reprezentację ma również każdy sygnał sinusoidalny:

u(t)↔U(t) ↔U(ω)

gdzie:

u(t)-rzeczywisty sygnał sinusoidalny (funkcja rzeczywista)
U(t)-sygnał zespolony przyporządkowany sygnałowi rzeczywistemu (funkcja zespolona zmiennej

rzeczywistej)

U(ω)-amplituda zespolona

u(t)=

cos

U

(ωt +

∠

U)

u(t)=

sin

U

(ωt +

∠

U)

U(t)=

cos

U

(ωt +

∠

U) + j

sin

U

(ωt +

∠

U)= U

(

)

U

t

e

∠

+

ω

= U

U

j

e

∠

e

jωt

= U e

jωt

gdzie:
U= U

U

j

e

∠

amplituda zespolona

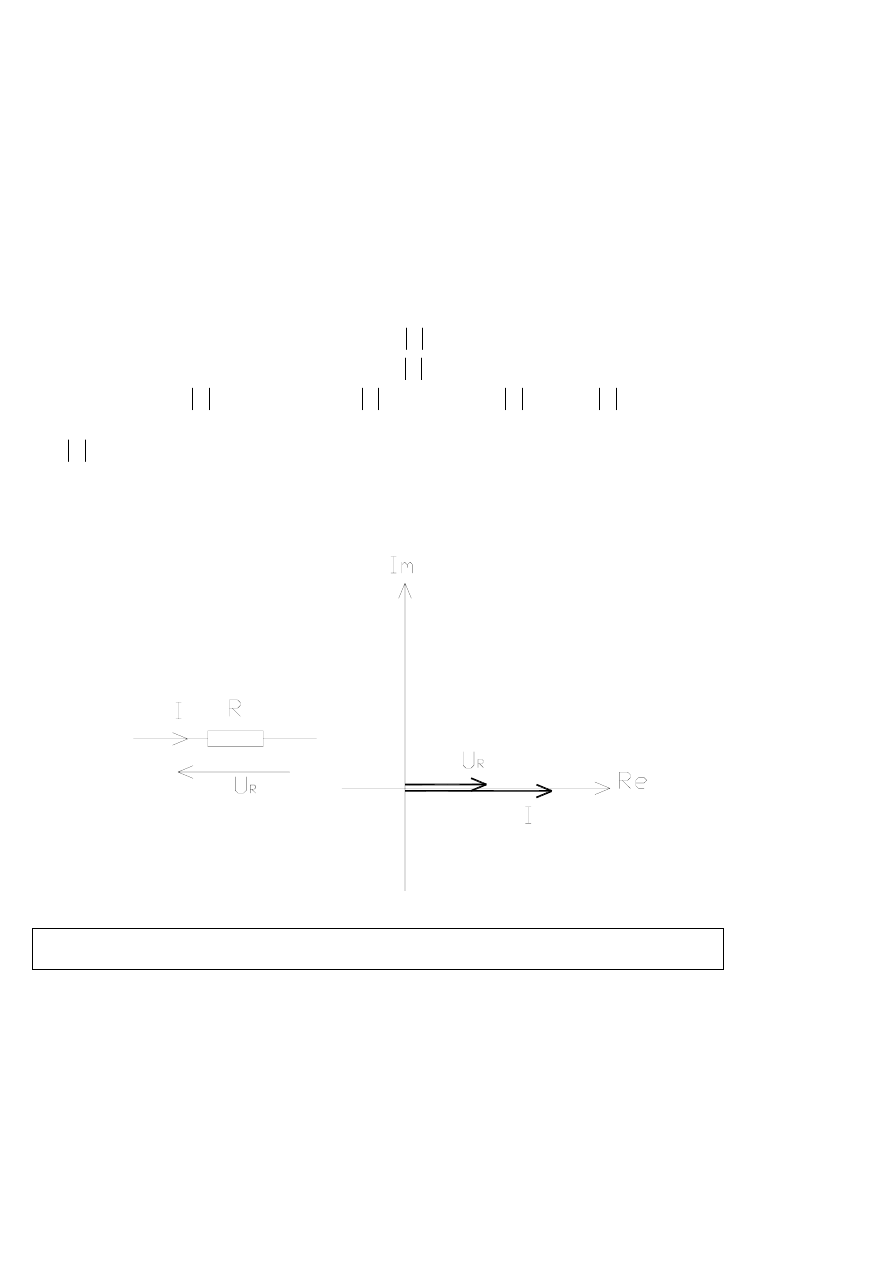
Rezystor:

R – rezystancja [Ω]

U

R

=RI – prawo Ohma wφ postaci zespolonej

Jak widać na powyższym wykresie wektorowym napięcie i prąd na rezystorze są ze sobą w fazie.

Mówimy, że taki obwód ma charakter rezystancyjny!

Cewka:

X

L

=ωL– reaktancja indukcyjna [Ω] U

L

= jωLI – prawo Ohma w postaci zespolonej

2

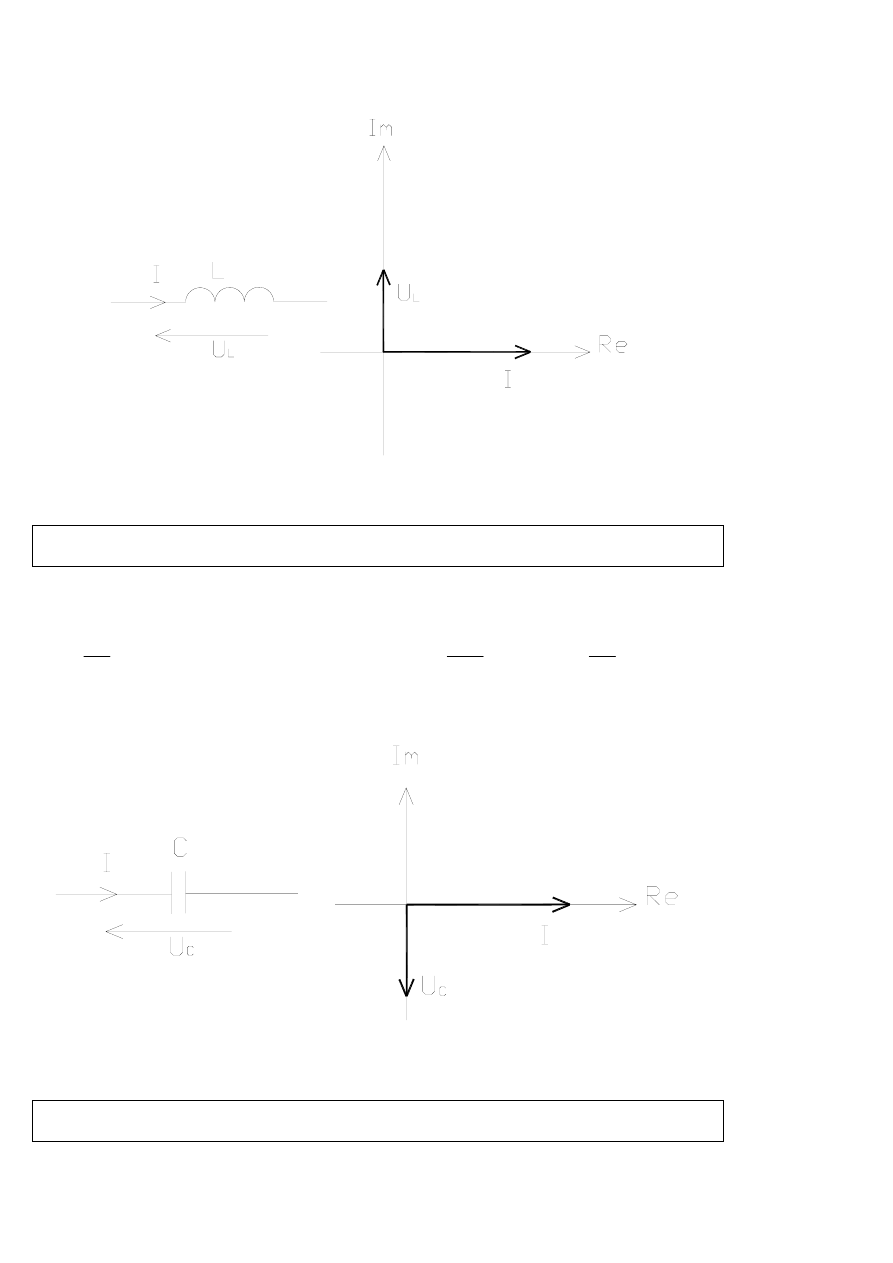
Jak widać na powyższym wykresie wektorowym napięcie na cewce wyprzedza prąd w fazie o 90°.

Mówimy, że taki obwód ma charakter indukcyjny!

Kondensator:

X

c

=

C

ω

1 - reaktancja pojemnościowa [s]

U

C

=

I

C

j

ω

1

U

C

=

∪

I

C

j

ω

1

−

– prawo Ohma w postaci

zespolonej

Jak widać na powyższym wykresie wektorowym napięcie na kondensatorze opóźnia się za prądem w fazie

o 90°. Mówimy, że taki obwód ma charakter pojemnościowy!

3

9

Połączenie szeregowe RLC

Z=R+jωL+

C

j

ω

1 =R+j

⎟

⎠

⎞

⎜

⎝

⎛

−

C

j

L

ω

ω

1

Na podstawie prawa Ohma w postaci zespolonej:

U=ZI

Moduł impedancji połączenia szeregowego:

2

2

1

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

C

L

R

Z

ω

ω

Argument impedancji połączenia szeregowego:

R

C

L

tg

ω

ω

ϕ

1

−

=

Wartości zespolone napięć na elementach idealnych:

U

R

=RI

U

L

= jωLI

C

=

I

C

j

ω

1

przy czym: U= U

R

+ U

L

+ U

C

Rozpatrujemy 3 przypadki:

1) ωL>

C

ω

1

Wówczas 0<φ<π/2 oraz U

L

> U

C

, a więc napięcie U wyprzedza prąd w fazie o kąt φ, wobec tego

połączenie ma charakter indukcyjny.

4

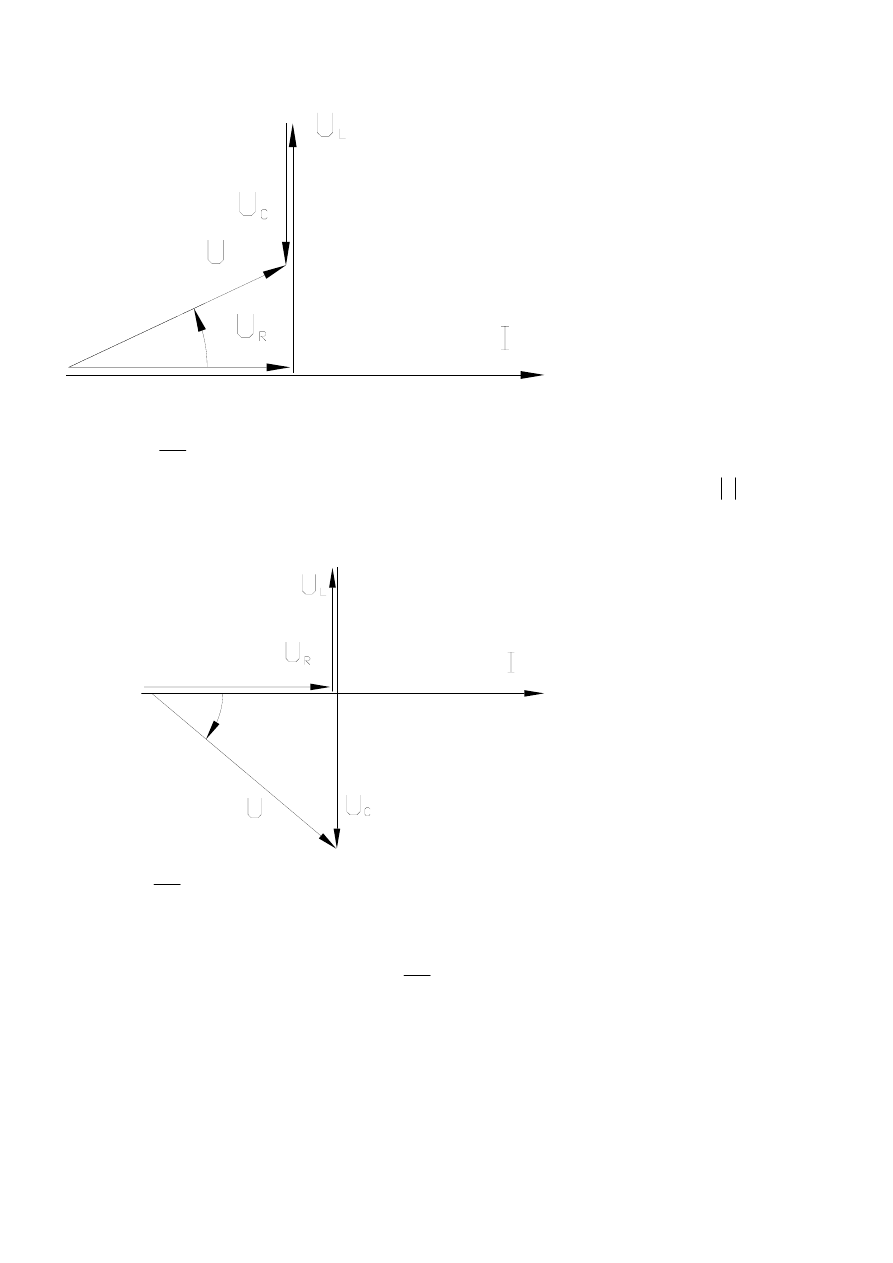
2) ωL<

C

ω

1

Wówczas - π/2< φ<0 oraz U

C

> U

L

, a więc prąd I wyprzedza w fazie napięcie U o kąt

ϕ

, wobec tego

połączenie ma charakter pojemnościowy.

3) ωL=

C

ω

1

Wówczas φ=0 oraz U

L

=U

C

, a więc napięcie U jest w fazie z prądem I. W rozpatrywanym przypadku

wpływ pojemności jest zrównoważony przez wpływ indukcyjności, gdy w połączeniu szeregowym

elementów RLC spełniona jest zależność ωL=

C

ω

1 mamy więc do czynienia z rezonansem napięć.

Warunkiem wystąpienia rezonansu napięć jest:

Im[Z]=0

5

9

Połączenie równoległe RLC

Y=G+

L

j

ω

1 +jωC=G+j

⎟

⎠

⎞

⎜

⎝

⎛

−

L

C

ω

ω

1

Na podstawie prawa Ohma w postaci zespolonej:

I=YU

Moduł admitancji połączenia równoległego:

2

2

1

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

L

C

G

Y

ω

ω

Argument admitancji połączenia szeregowego (jest nim – φ):

( )

G

L

C

tg

ω

ω

ϕ

1

−

=

−

⇒

( )

⎟

⎠

⎞

⎜

⎝

⎛

−

=

C

L

G

tg

ω

ω

ϕ

1

1

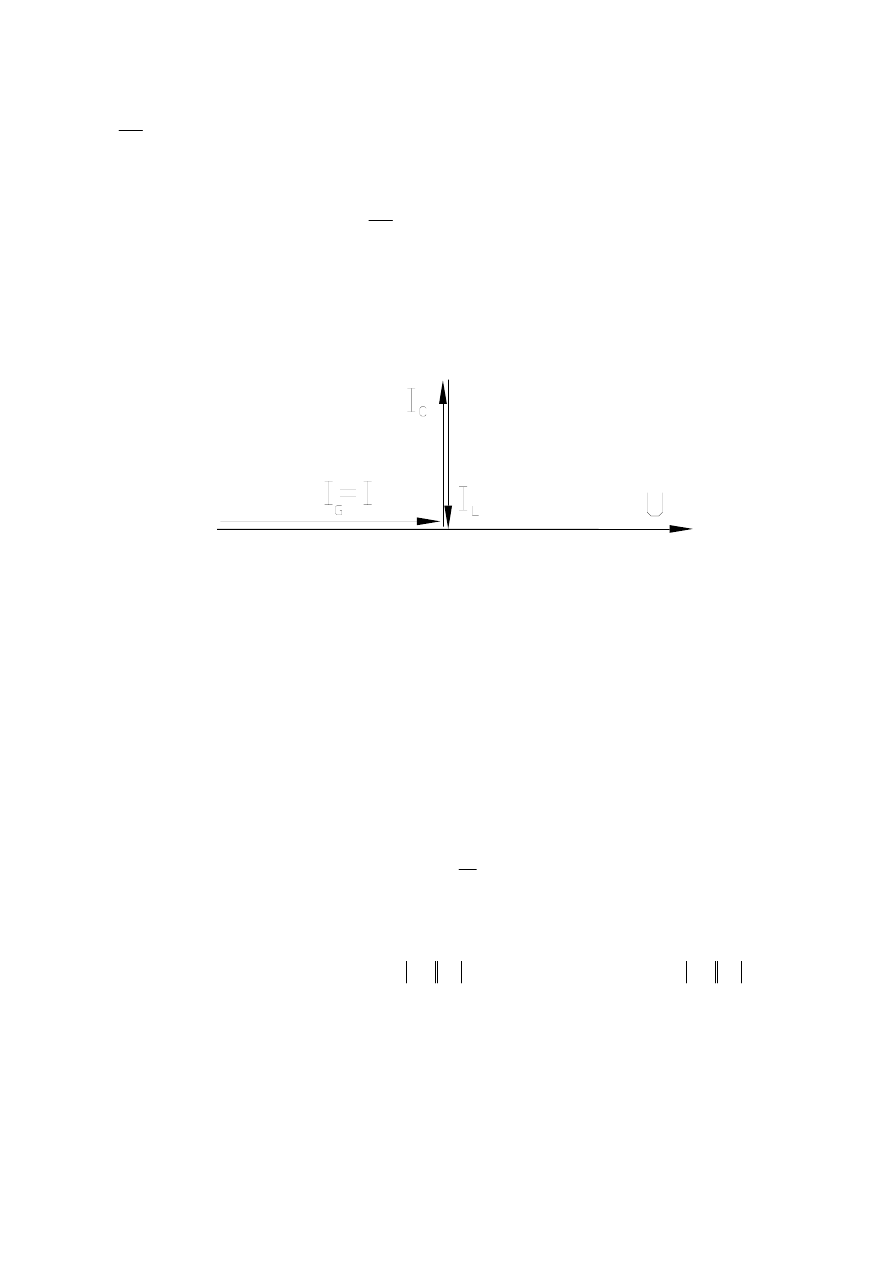
Wartości zespolone prądów na elementach idealnych:

I

G

=GU I

L

=

L

j

U

ω

I

C

=jωCU

6

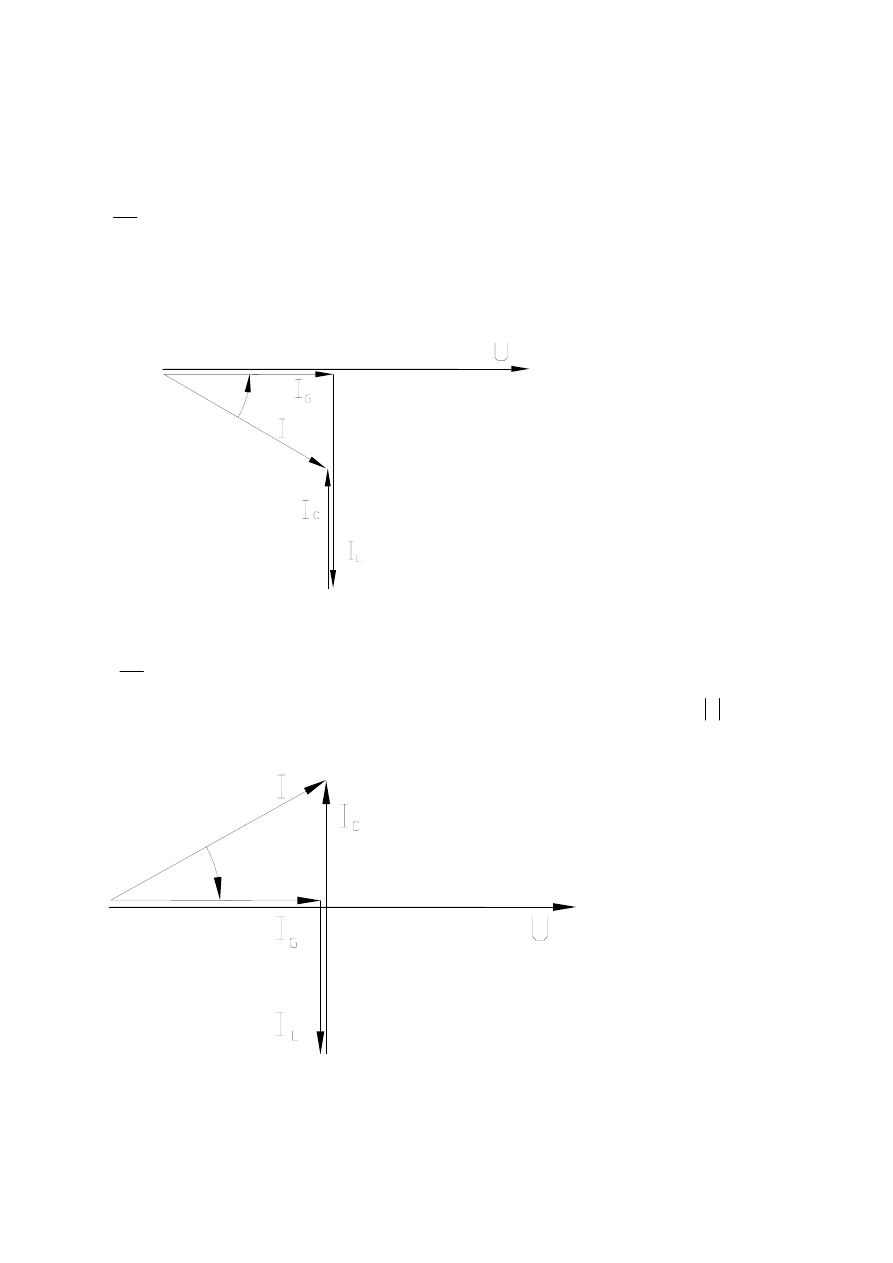
przy czym: I= I

G

+ I

L

+ I

C

Rozpatrujemy 3 przypadki:

1)

L

ω

1 >ωC

Wówczas 0<φ<π/2 oraz I

L

> I

C

, a więc napięcie U wyprzedza w fazie prąd I o kąt φ, wobec tego

połączenie ma charakter indukcyjny.

2)

L

ω

1 < ωC

Wówczas - π/2< φ<0 oraz I

L

<I

C

, a więc prąd I wyprzedza w fazie napięcie U o kąt

ϕ

, wobec tego

połączenie ma charakter pojemnościowy.

7

3)

L

ω

1 = ωC

Wówczas φ=0, a więc prąd I jest w fazie z napięciem U. W rozważanym przypadku wpływ

indukcyjności jest zrównoważony przez wpływ pojemności, gdy w połączeniu równoległym

elementów RLC spełniona jest zależność

L

ω

1 = ωC mamy, więc do czynienia z rezonansem prądów.

Warunkiem wystąpienia rezonansu prądów jest:

Im[Y]=0

9

Rezonans

Rezonansem nazywamy taki stan dwójnika, w którym reaktancja X lub susceptancja B dwójnika jest
równa zeru. Warunkiem wystąpienia rezonansu jest

(*)

X=Im[Z]=0 – w przypadku rezonansu napięć

(**) B=Im[Y]=0 – w przypadku rezonansu prądów

O czym wspomniane było wyżej.
Ponieważ kąt φ przesunięcia fazowego między napięciem a prądem jest równy argumentowi

impedancji Z, przy czym

R

X

tg

=

ϕ

więc tg φ=0 dla X=0. Oznacza to, że w stanie rezonansu napięcie U dwójnika jest w fazie z prądem I.
Do tego samego wniosku dochodzi się, biorąc pod uwagę, że w stanie rezonansu susceptancja B

dwójnika równa się zeru.
W stanie rezonansu Moz bierna dwójnika

ϕ

sin

sk

sk

I

U

Q

=

=0, a moc czynna

ϕ

cos

sk

sk

I

U

Q

=

=UI,

ponieważ φ=0.

Elementy L i C w układzie R, L, C, w którym wystąpił rezonans napięć zachowują się jak zwarcie. W
przypadku układu R, L, C, w którym wystąpił rezonans prądów elementy L i C zachowują się jak

przerwa.

Rezonans w obwodach elektrycznych może występować przy jednej lub przy kilku wartościach
pulsacji zwanych pulsacjami rezonansowymi. Pulsacje rezonansowe dwójnika wyznacza się z równań

(*) oraz (**)

8

Przykład:

Obliczyć prądy i napięcia na elementach układu:

Dane:

e(t)=100sinωt

f=50[Hz]
R

1

=2[Ω]

R

2

=8[Ω]

4

1

1

1

=

=

C

L

ω

ω

[Ω]

6

1

2

2

=

=

C

L

ω

ω

[Ω]

Szukane:

U

R1

=?

U

R2

=?

U

L2

=?

U

C2

=?

I=?

I

1

=?

I

2

=?

I

3

=?

I

4

=?

Rozwiązanie:

9

[ ]

V

e

E

j

sk

100

100

0

=

=

D

1

Z -impedancja zastępcza elementów L

1

i C

1

połączonych równolegle

(

)

∞

=

−

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

=

4

4

4

4

1

1

1

1

1

1

1

j

C

L

j

C

j

L

j

Z

ω

ω

ω

ω

⇒

[ ]

0

1

1

Im

1

1

=

∞

=

=

Z

Y

→ Jest to rezonans prądów

Ponieważ na elementach L

1

i C

1

mamy do czynienia z rezonansem prądów układ w tym miejscu

traktujemy jak przerwę w obwodzie. Dochodzimy więc do wniosku, że prądy:

I

1

=0

oraz ponieważ

I

1

=I

3

+I

4

I

3

+I

4

=0

I

3

=-I

4

⇒

⇒

1

34

3

L

j

U

I

ω

=

C

j

U

I

ω

1

34

4

−

=

Musimy więc znaleźć napięcie U

34

Ponieważ

I=I

2

oraz

Z

2

-impedancja zastępcza elementów L

2

i C

2

połączonych szeregowo

(

)

0

6

6

1

2

2

2

=

−

=

−

=

j

C

j

L

j

Z

ω

ω

⇒

Im[Z

2

]=0 → Jest to rezonans napięć

Ponieważ na elementach L

2

i C

2

mamy do czynienia z rezonansem napięć układ w tym miejscu

traktujemy jak zwarcie w obwodzie. Dochodzimy do wniosku, że napięcie

0

1

2

2

2

2

2

2

=

−

=

+

=

I

C

j

I

L

j

U

U

U

C

L

ω

ω

Na powyższym zredukowanym schemacie widać, że

10

[ ]

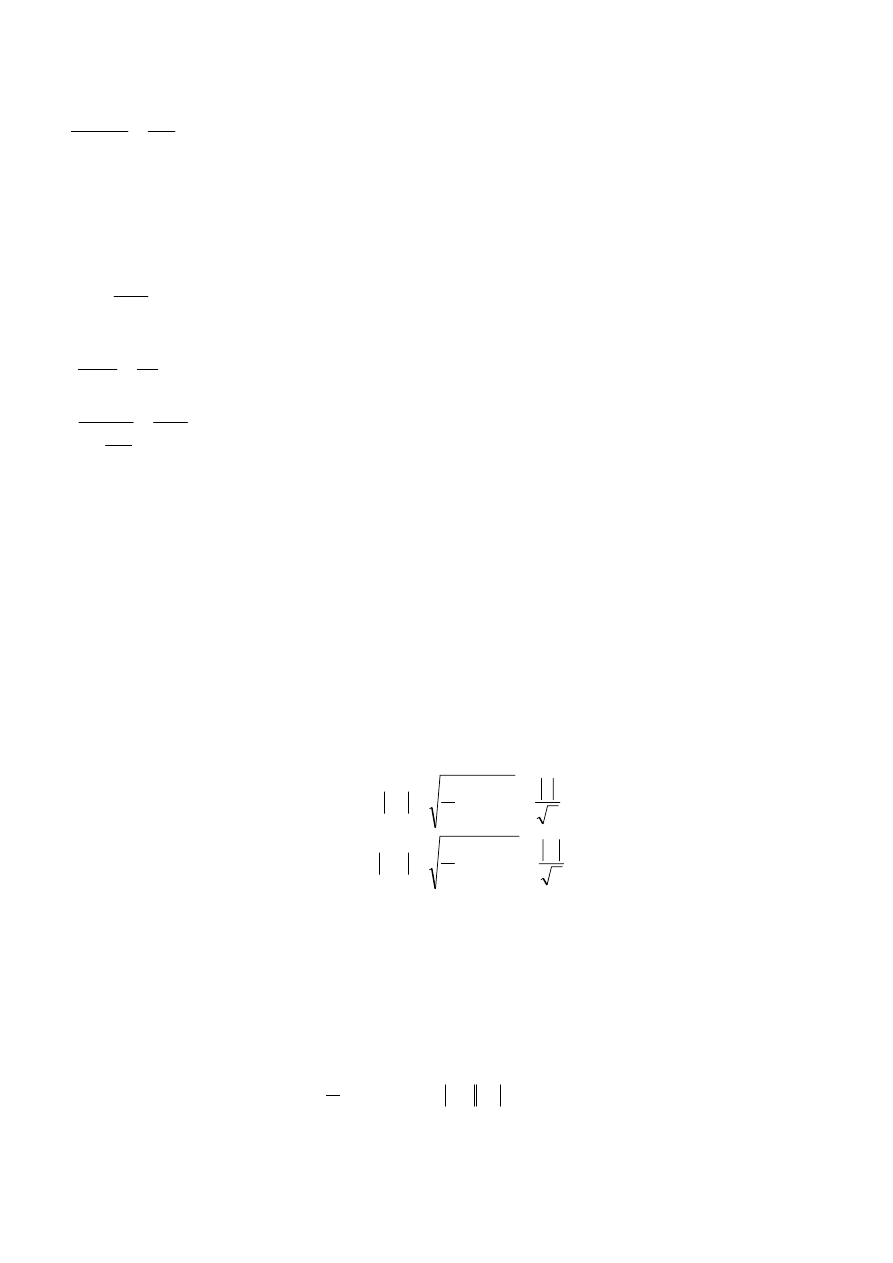
2

2

1

10

10

100

I

A

R

R

E

I

sk

=

=

=

+

=

Przechodzimy do obliczania napięć na poszczególnych elementach obwodu:

[ ]

[ ]

V

e

I

R

U

j

R

D

0

1

1

1

40

40

10

2

=

Ω

=

⋅

=

⋅

=

[ ]

[ ]

34

0

2

2

2

40

80

10

8

U

V

e

I

R

U

j

R

=

=

Ω

=

⋅

=

⋅

=

D

[ ]

[ ]

V

e

V

j

j

I

L

j

U

j

L

D

90

2

2

2

60

60

10

6

=

=

⋅

=

=

ω

[ ]

[ ]

V

e

V

j

j

I

C

j

U

j

C

D

90

2

2

2

60

60

10

6

1

−

=

−

=

⋅

−

=

−

=

ω

Ponieważ znaleźliśmy napięcie U

34

możemy wyliczyć prądy

[ ]

[ ]

A

e

A

j

j

L

j

U

I

j

D

90

1

34

3

20

20

4

80

−

=

−

=

=

=

ω

[ ]

[ ]

A

e

A

j

j

C

j

U

I

j

D

90

34

4

20

20

4

80

1

=

=

−

=

−

=

ω

Na koniec możemy zapisać obliczone prądy i napięcia w funkcjach czasu:

t

t

i

t

i

ω

sin

10

)

(

)

(

2

=

=

0

)

(

1

=

t

i

(

)

D

90

sin

20

)

(

3

−

=

t

t

i

ω

(

)

D

90

sin

20

)

(

4

+

=

t

t

i

ω

20

1

=

R

u

20

34

2

=

= u

u

R

(

)

D

90

sin

60

)

(

2

+

=

t

t

u

L

ω

(

)

D

90

sin

60

)

(

2

−

=

t

t

u

C

ω

9

Moc w obwodzie prądu sinusoidalnego

1) Wartość skuteczna prądu sinusoidalnego i napięcia:

( )

2

1

0

2

I

dt

t

i

T

I

T

sk

=

=

∫

( )

2

1

0

2

U

dt

t

u

T

U

T

sk

=

=

∫

2) Moc chwilowa:

p=ui

Moc chwilowa jest dodatnia w przedziałach czasu, w których napięcie

u

oraz prąd

i

mają znaki

jednakowe – ujemna zaś w przedziałach czasu, w których znaki napięcia

u

oraz prądu

i

są różne.

Jeżeli p>0 to energia elektryczna jest dostarczana ze źródła do odbiornika; jeżeli natomiast p<0 to

energia jest zwracana do źródła przez odbiornik, który przekazuje energię nagromadzoną w polu
magnetycznym cewek i w polu elektrycznym kondensatorów.

3) Moc czynna:

ϕ

ϕ

cos

cos

1

0

sk

sk

T

I

U

dt

UI

T

P

=

=

∫

[W]

11

Moc czynna jest równa iloczynowi wartości skutecznych napięcia i prądu oraz kosinusa kata

przesunięcia fazowego między napięciem i prądem. Współczynnikiem mocy nazywamy kosinusa kata
przesunięcia fazowego między napięciem i prądem (cosφ). Moc czynna jest nieujemna, wartość

największą (P=UI) moc osiąga wtedy, gdy φ=0 (odbiornik ma charakter rezystancyjny, cosφ=1),

wartość najmniejszą (P=0) w przypadku granicznym, gdy φ=±π/2 (wtedy odbiornikiem jest idealna
cewka lub idealny kondensator, cosφ=0).

4) Moc bierna:

ϕ

sin

sk

sk

I

U

Q

=

[VAr]

W przypadku odbiornika indukcyjnego charakterze indukcyjnym mamy Q>0,bo 0<φ<π/2, a w

przypadku odbiornika o charakterze pojemnościowym mamy Q<0, bo -π/2< φ<0.

5) Moc pozorna:

sk

sk

I

U

S

=

[VA]

6) Moc zespolona

S=UI*

Mamy:

S=

ϕ

ϕ

sin

cos

sk

sk

sk

sk

I

U

j

I

U

+

=P + jQ

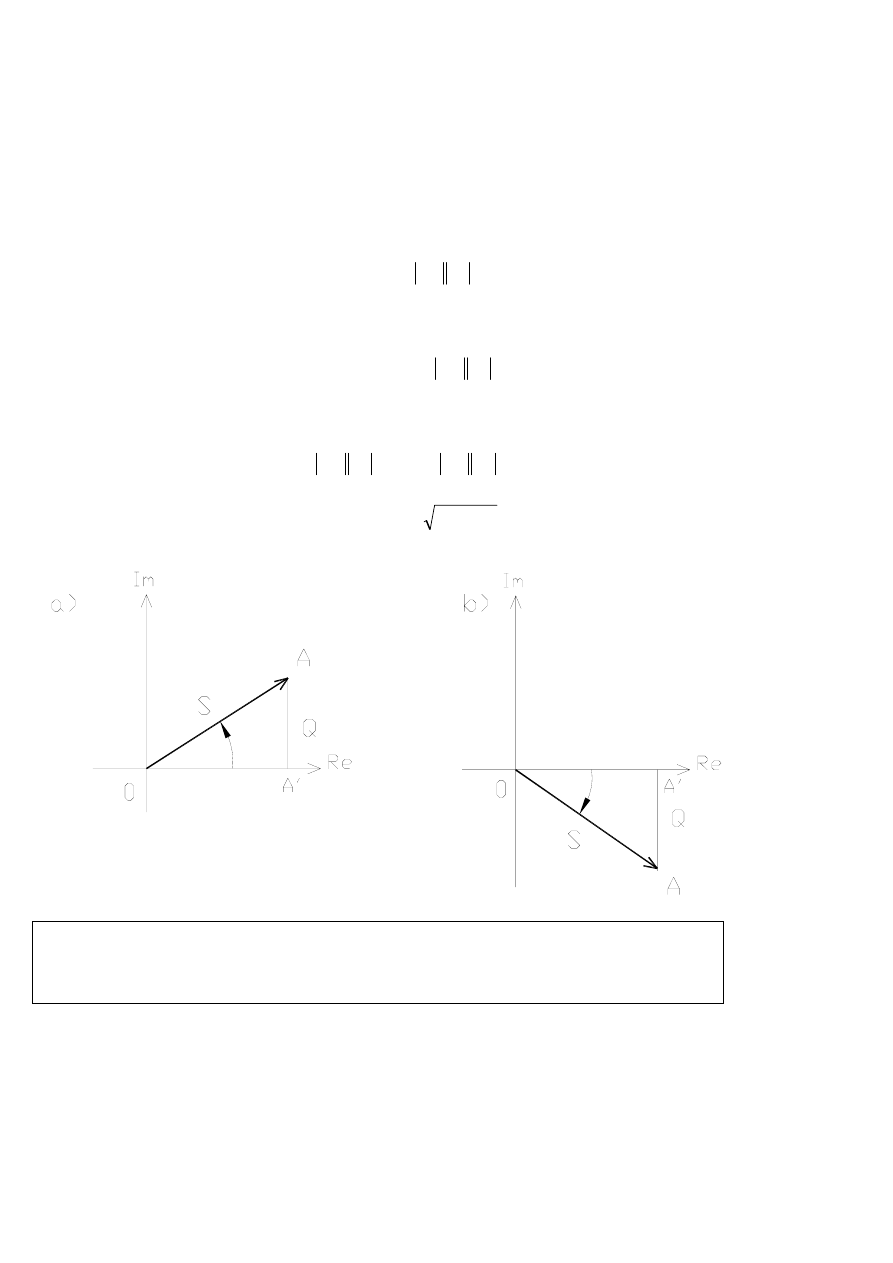
Oraz:

2

2

Q

P

S

+

=

Rys. a) Trójkąt mocy układu o charakterze indukcyjnym, ponieważ kąt φ jest dodatni, 0<φ< π/2,a więc

Q=U

sk

I

sk

sinφ>0

Rys. b) Trójkąt mocy układu o charakterze pojemnościowym, ponieważ kąt φ jest ujemny, -π/2<φ<0, a

więc Q=U

sk

I

sk

sinφ<0

Przykład:

7) Kompensacja mocy biernej:

12

Dane:
P=600 [W]

sk

I =4,55 [A]

sk

U =220 [V]

f=50 [Hz]

Mamy dobrać kondensator do poprawy współczynnika mocy do wartości 0,9 oraz narysować wykres
wektorowy przed kompensacją i po kompensacji.

Przed kompensacją:

ponieważ:

'

10

53

6

,

0

55

,

4

220

600

cos

cos

°

=

⇒

=

⋅

=

=

⇒

=

ϕ

ϕ

ϕ

sk

sk

sk

sk

I

U

P

I

U

P

, tgφ=1,335

cosφ’=0,9

⇒

φ’=25˚50’, tgφ’=0,484

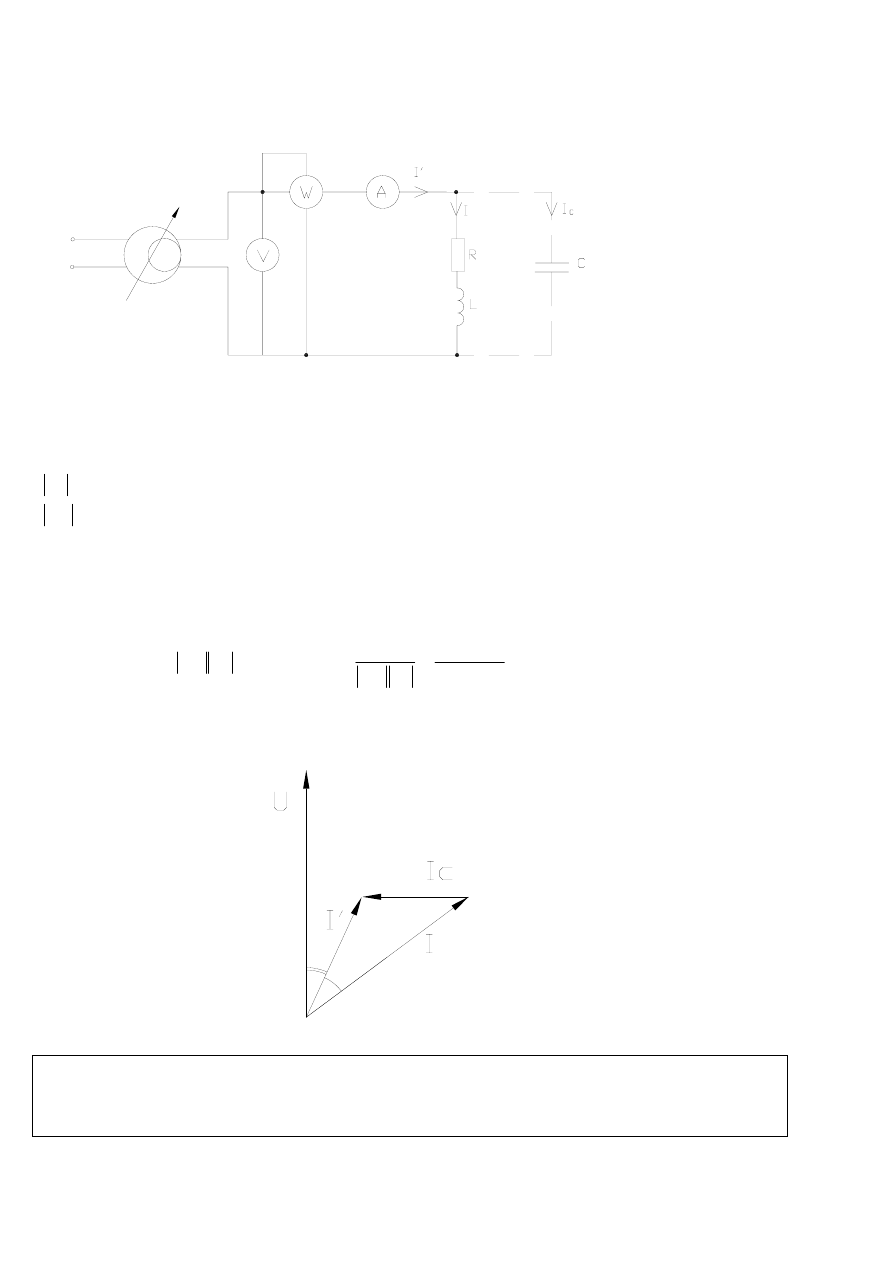
Wykres topograficzny:

Na powyższym wykresie wskazowym widać napięcie U oraz prąd I przed kompensacją, które przesunięte są o

obliczony w zadaniu kąt φ. Po kompensacji mocy biernej kąt φ’ zmniejszył się w stosunku do kąta φ co jest

spowodowane pojawieniem się prądu I

C

płynącego przez kondensator, który to wyprzedza napięcie w fazie o

90°.Suma wektorowa prądów I oraz I

C

daje wypadkowy wektor prądu I’

13

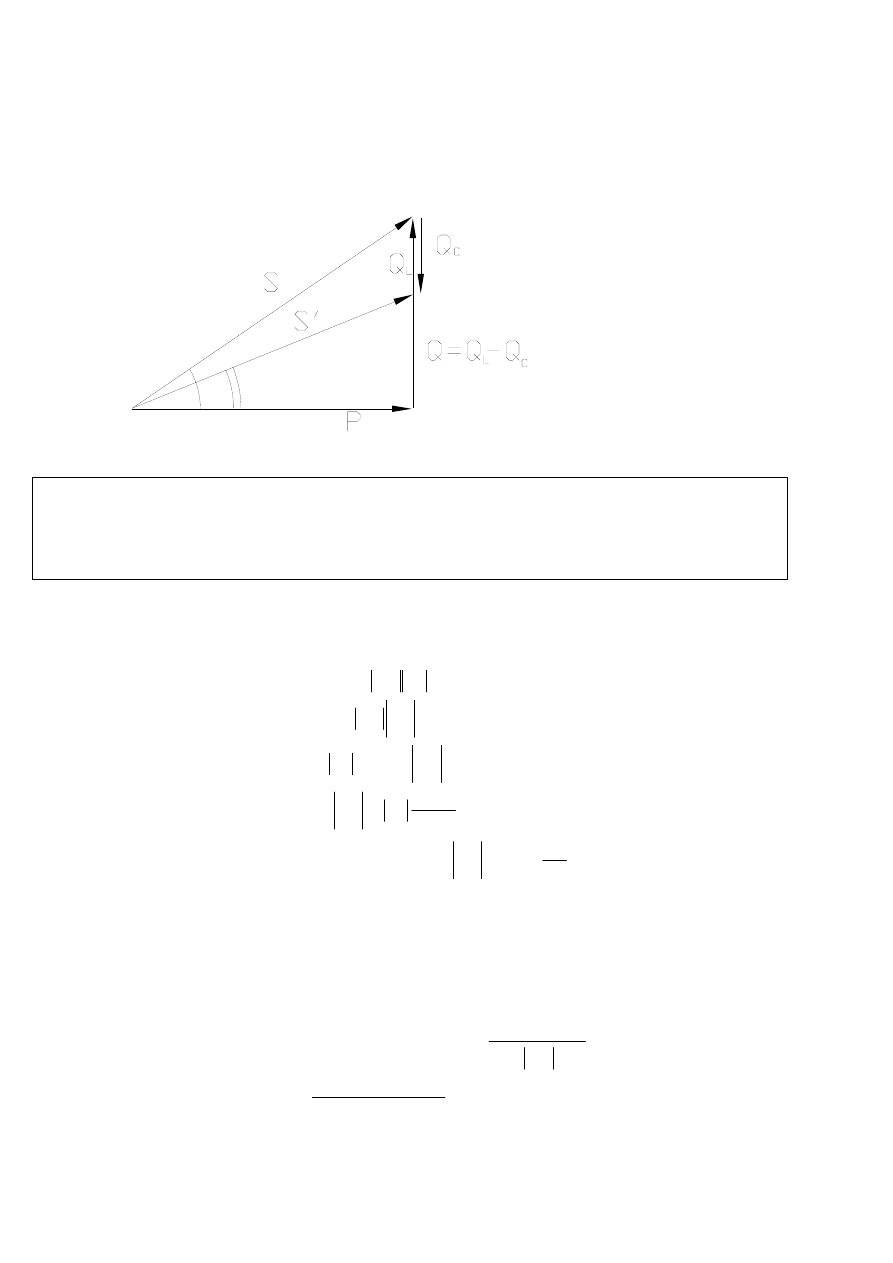
Trójkąt mocy:

Powyższy wykres wektorowy przedstawia zmianę mocy. Przed kompensacją na rezystancji R odkładała się moc

czynna P a na indukcyjności L odkładała się moc bierna Q

L

przesunięta o kąt π/2 w stosunku do mocy czynnej P,

współczynnik mocy wynosił cosφ. Po kompensacji mocy biernej na dołączonej pojemności C odłożyła się moc bierna

Q

C

przesunięta o kąt –π w stosunku do mocy Q

L

, obie moce odjęte wektorowo dają wypadkową moc Q, nową moc

pozorną S’ oraz nowy, poprawiony współczynnik mocy cosφ’.

A więc po kompensacji U oraz I są takie same, P jest również taka sama ponieważ dołączony

kondensator pobiera tylko moc bierną.
Przed kompensacją:

P=

ϕ

cos

sk

sk

I

U

Po kompensacji:

ϕ

′

′

cos

sk

sk

I

U

stąd:

ϕ

cos

sk

I

=

ϕ

′

′

cos

sk

I

czyli:

ϕ

ϕ

′

=

′

cos

cos

sk

sk

I

I

[A]

W naszym przykładzie: 03

,

3

9

,

0

6

,

0

55

,

4

=

⋅

=

′

sk

I

[A]

Na podstawie trójkąta mocy wiemy, że:

Q

L

=P·tgφ

Q= P·tgφ’

Q

L

- Q

C

= P·tgφ’

⇒

P·tgφ- Q

C=

P·tgφ’

Q

C

=P(tgφ-tgφ’)

ponieważ: Q

C

=X

C

·│I

sk

│

2

=│U

sk

│

2

·ωC

więc:

│U

sk

│

2

·ωC= P(tgφ-tgφ’)

⇒

(

)

2

'

sk

U

tg

tg

P

C

ω

ϕ

ϕ

−

=

W naszym przykładzie:

(

)

6

,

33

220

314

484

,

0

335

,

1

600

2

=

⋅

−

=

C

[µF]

14

32

,

2

=

⋅

=

=

C

U

X

U

I

sk

C

sk

skC

ω

[A]

9

Wyznaczenie U

RL

i U

L

w układzie szeregowym RLC na podstawie znajomości zmierzonych

napięć U

1

U

R

i U

LR

, czyli metodą „trzech woltomierzy”:

Na podstawie rys.1 wiemy, że (podkreśleniem zaznaczono liczby zespolone):

LR

R

U

U

U

+

=

1

Po podstawieniu obu stron równania do skalarnego kwadratu otrzymujemy:

ϕ

cos

2

2

2

2

1

LR

R

LR

R

U

U

U

U

U

+

+

=

oraz

LR

R

LR

R

U

U

U

U

U

2

cos

2

2

2

1

−

−

=

ϕ

Wiemy, że:

U

R

=R

L

·I oraz U

L

=X

L

·I

Na podstawie wykresu:

U

R

=U

LR

cosφ oraz U

L

=U

LR

sinφ

stąd:

I

U

I

U

R

LR

R

L

ϕ

cos

=

=

I

U

I

U

X

LR

L

L

ϕ

sin

=

=

Znajomość wartości X

L

umożliwia obliczenie indukcyjności L cewki rzeczywistej.

15

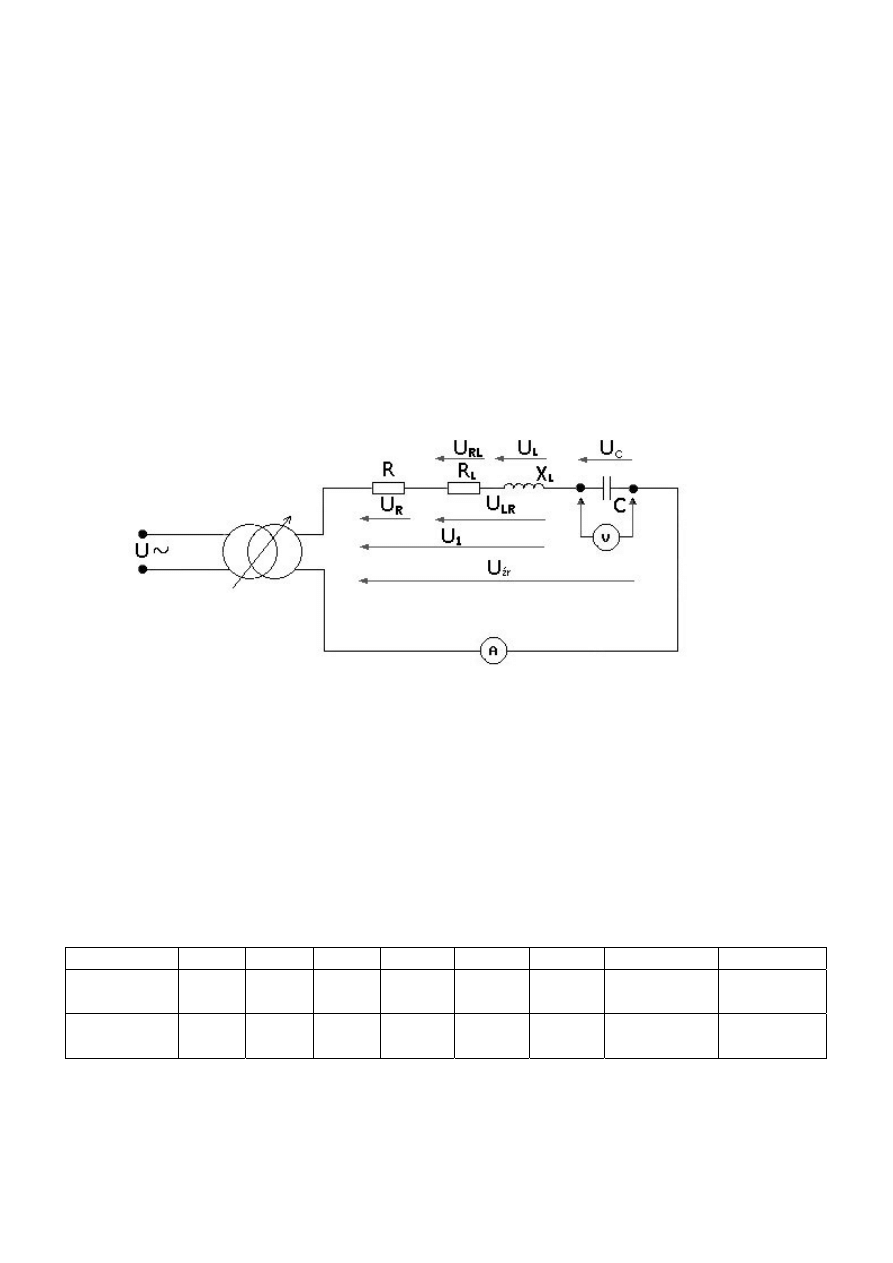
Program ćwiczenia:

1) Pomiar napięć i prądów w obwodzie szeregowym RLC

2) Pomiar napięć i prądów w obwodzie równoległym RLC
3) Kompensacja mocy biernej odbiornika RL

Wykonanie ćwiczenia:

I.

Łączymy układ szeregowy RLC jak na poniższym schemacie:

Rys.1

Dokonujemy pomiarów prądów oraz napięć na elementach R,L,C oraz na źródle. Otrzymane wyniki

zapisujemy w tabeli nr1.
Dokonujemy sprawdzenia wyników pomiarów napięć i prądu na podstawie znajomości napięcia

źródłowego i parametrów R,R

L

, L, C, f otrzymane wyniki zapisujemy w tabeli nr1.

Na podstawie zmierzonych wartości napięć ma prądu rysujemy wykres wskazowy napięć ma prądu

przyjmując odpowiednie skale.

Tabela nr1

U

źr

[V] I[mA] U

LR

[V]

U

1

[V] U

C

[V] U

R

[V] U

L

[V] U

R

L

[V]

Wielkości

mierzone

x x

Wielkości

wyliczone

x x x x x x

16

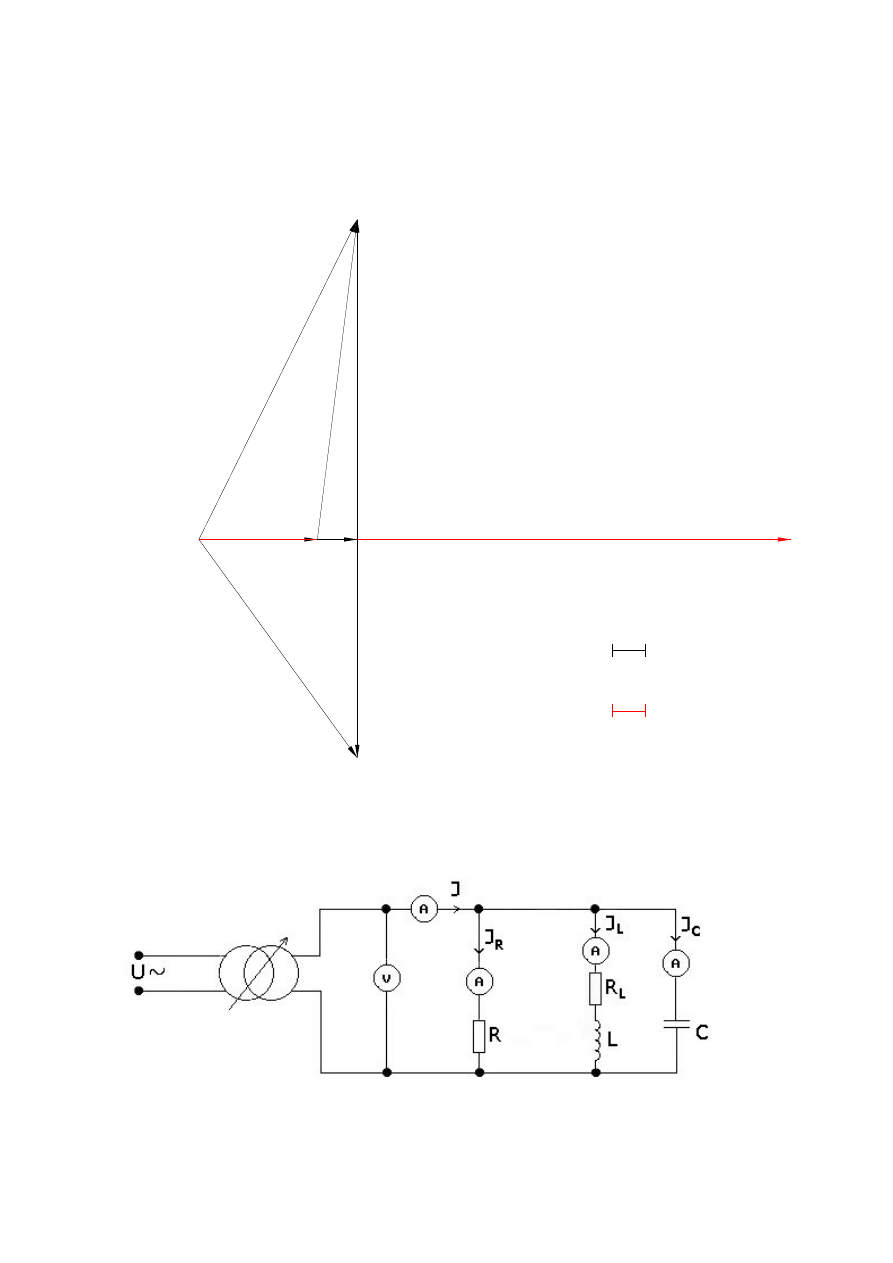
10V

10A

I

U

źr

U

C

U

R

U

R

L

U

L

U

1

U

LR

rys. 1 : Wykres wskazowy prądu i napięć -

poł. szeregowe RLC

II. Łączymy układ równoległy RLC jak na poniższym schemacie:

Rys. 2

17

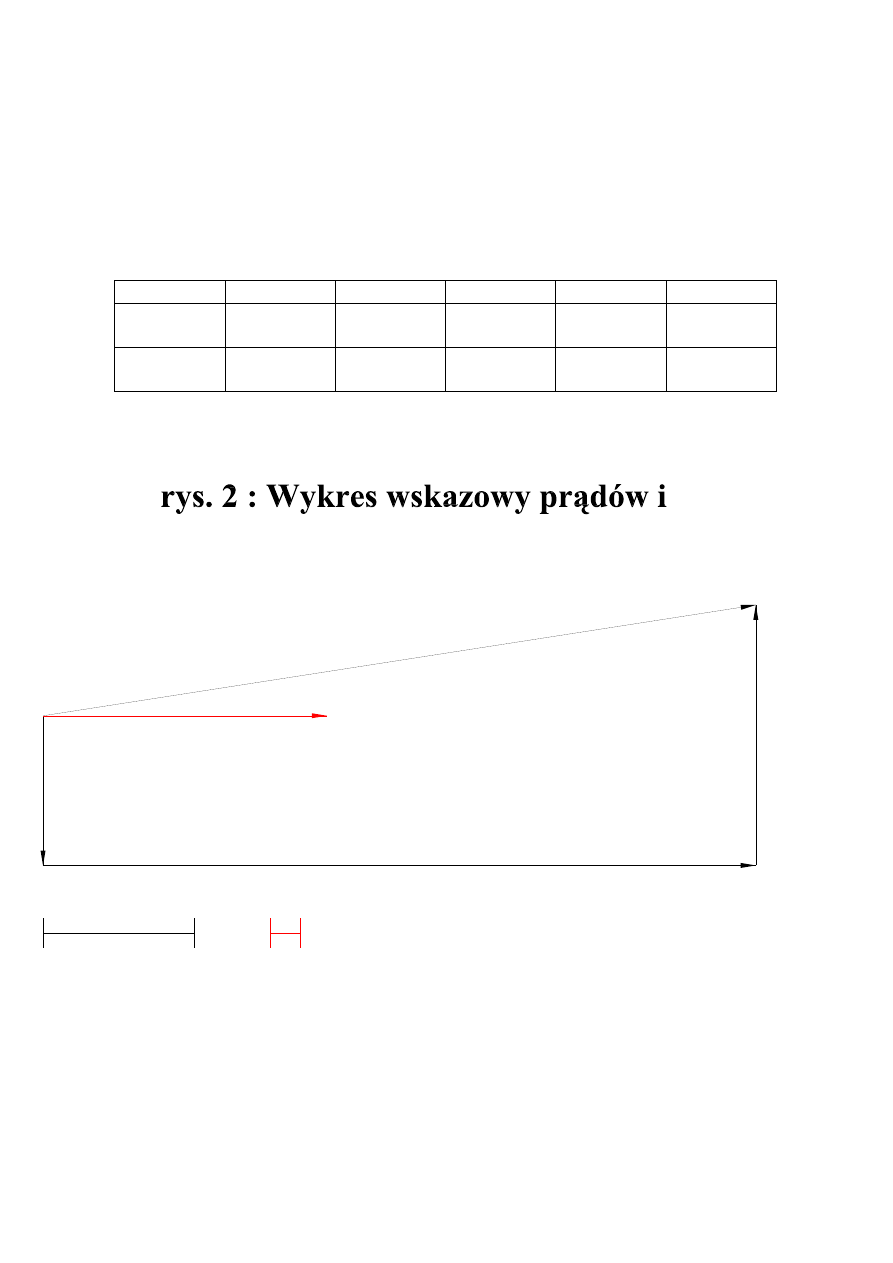
Dokonujemy pomiarów prądów I, I

R

, I

L

, I

C

oraz napięcia. Otrzymane wyniki zapisujemy w tabeli nr2.

Dokonujemy sprawdzenia wyników pomiarów napięcia i prądów na podstawie znajomości R, L, C, f
oraz napięcia U - otrzymane wyniki zapisujemy w tabeli nr2.

Na podstawie obliczeń prądów i danego napięcia U rysujemy wykres wskazowy napięcia i prądów

przyjmując odpowiednie skale.

Tabela nr2

U[ma]

I[A] I

R

[A] I

L

[A] I

C

[A]

Wielkości

mierzone

Wielkości

wyliczone

100mA

10V

U

I

C

I

R

I

L

I

napięcia - poł. równoległe RLC

18

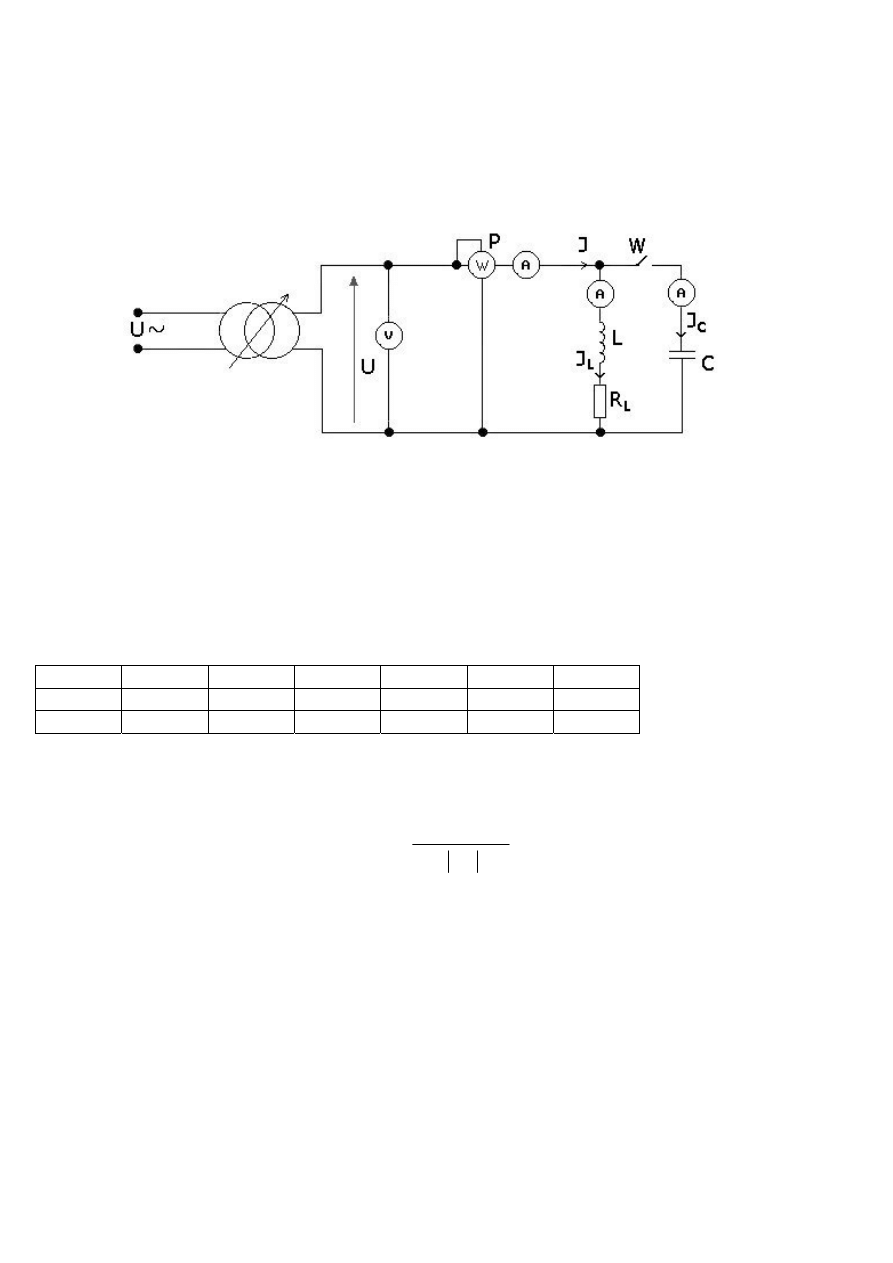
III. Kompensacja mocy biernej:

Łączymy układ jak na poniższym schemacie:

Rys.3

Dokonujemy pomiarów napięcia , mocy i prądów najpierw dla obwodu szeregowego R, L a następnie
po dołączeniu równolegle kondensatora do odbiornika. Otrzymane wyniki zapisujemy w tabeli nr3.

Na podstawie pomiarów rysujemy wykres wskazowy.

Tabela nr3

U[V] I[mA] I

RL

[mA] I

C

[mA] P[W] cosφ S[VA]

Wyznaczamy pojemność kondensatora na podstawie wzoru:

(

)

2

'

sk

U

tg

tg

P

C

ω

ϕ

ϕ

−

=

19

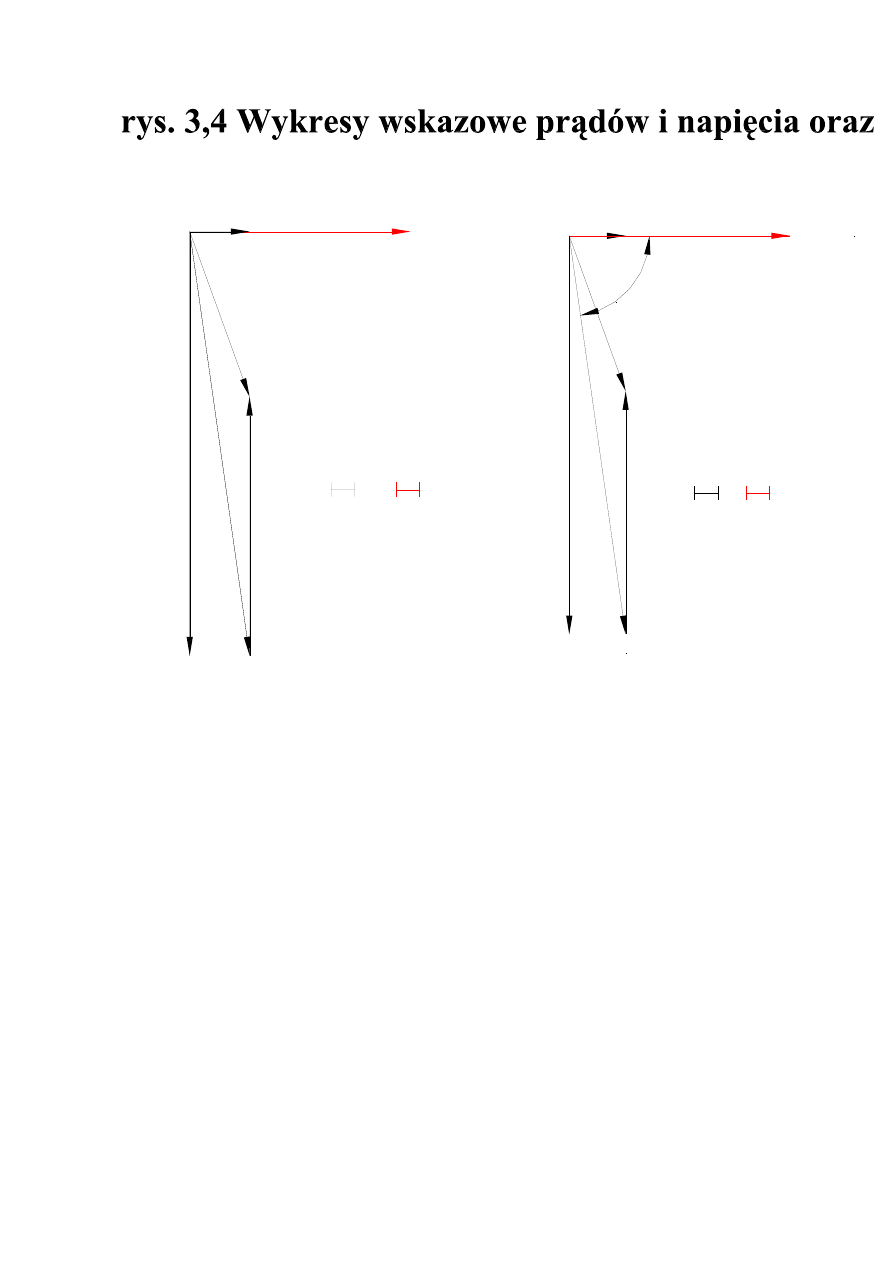
10mA

10V

U

I

Icos

ϕ

Isin

ϕ

I

C=3,5

µF

I

komp

U

10V

1W

Q

Q

C

S

S

komp

P

ϕ

mocy przy kompensacji mocy biernej

20