Ćwiczenia 2

1. Wyznaczyć dziedzinę funkcji f określonej wzorem:
a) fx  x

2

 2x − 15 ;

b) fx 

1

x

2

−4

;

c) fx  log

2

5x

−6−x

2

x

2

4x11

;

d) fx  log

2

log

x

x  1.

2. Wyznaczyć dziedzinę i zbiór wartości funkcji f określonej wzorem:
a) fx  4 − x

2

;

b) fx  2x − 6  6 − 2x ;

c) fx 

2

−x3

x

1

− 1;

d) fx  5  |x  2|;

e) fx 

x

3x

2

5

.

3. Dana jest funkcja fx 

x

2

2

x

2

1

określona w zbiorze

. Wykaż, że zbiorem wartości tej funkcji

jest przedział 1, 2.

4. Czy funkcje f i g są równe?
a) fx  x

2

, gx  x;

b) fx  x

2

, gx 

x

4

x

2

;

c) fx 

|x

−2|

x

−2

, gx  1;

d) fx 

x

4

−1

x

2

1

, gx  x

2

− 1.

5. Na podstawie definicji sprawdzić, że funkcja f jest:
a) fx  x  1 ←rosnąca;

b) fx 

1

x

dla x

∈ 



← malejąca;

c) fx  x

2

dla x

∈ 

−

← malejąca;

d) fx 

x

2

x

−1

dla x

∈ −, 1 ← malejąca.

6. Czy funkcja fx 

x

−2

x

2

−2x

ma miejsce zerowe?

7. Wykazać, że funkcja fx 

ax

b

cx

d

, ad

≠ bc, c ≠ 0 jest różnowartościowa.

8. Zbadać parzystość funkcji f:
a) fx  x

6

− 2x

4

 8;

b) fx  |x|  x;

c) fx  sin

2

x;

d) fx 

cos x

x

;

e) fx 

sin x

x

;

f) fx 

1

x

−3

;

g) fx 

3x

4

x−2x1

.

9. Pokazać, że funkcja f posiada w punkcie x

o

:

a) fx  1 − 2x − 3x

2

, x

o

 −

1
3

maksimum;

b) fx  x

2

− 2x − 5, x

o

 1 minimum.

10. Wyznaczyć największą i najmniejszą wartość funkcji fx  x

3

w przedziale 〈−1, 1.

11. Wyznacz funkcję odwrotną do funkcji f:
a) fx 

ax

b

cx

d

, ad

≠ bc, c ≠ 0;

b) fx  log

3

3x ;

c) fx  2

4x

1

;

d) fx 

x

1

−|x|

.

12. Dane są funkcje f i g. Wyznaczyć f

∘ g oraz g ∘ f:

a) fx 

1

x

3

, gx  x ;

b) fx  cos x  3, gx  x

2

 2x;

c) fx  sin

2

4x, g

x  log 3x;

d) fx  log x , gx  x

2

;

e) fx  1 − sin 2x , gx  log 2x.

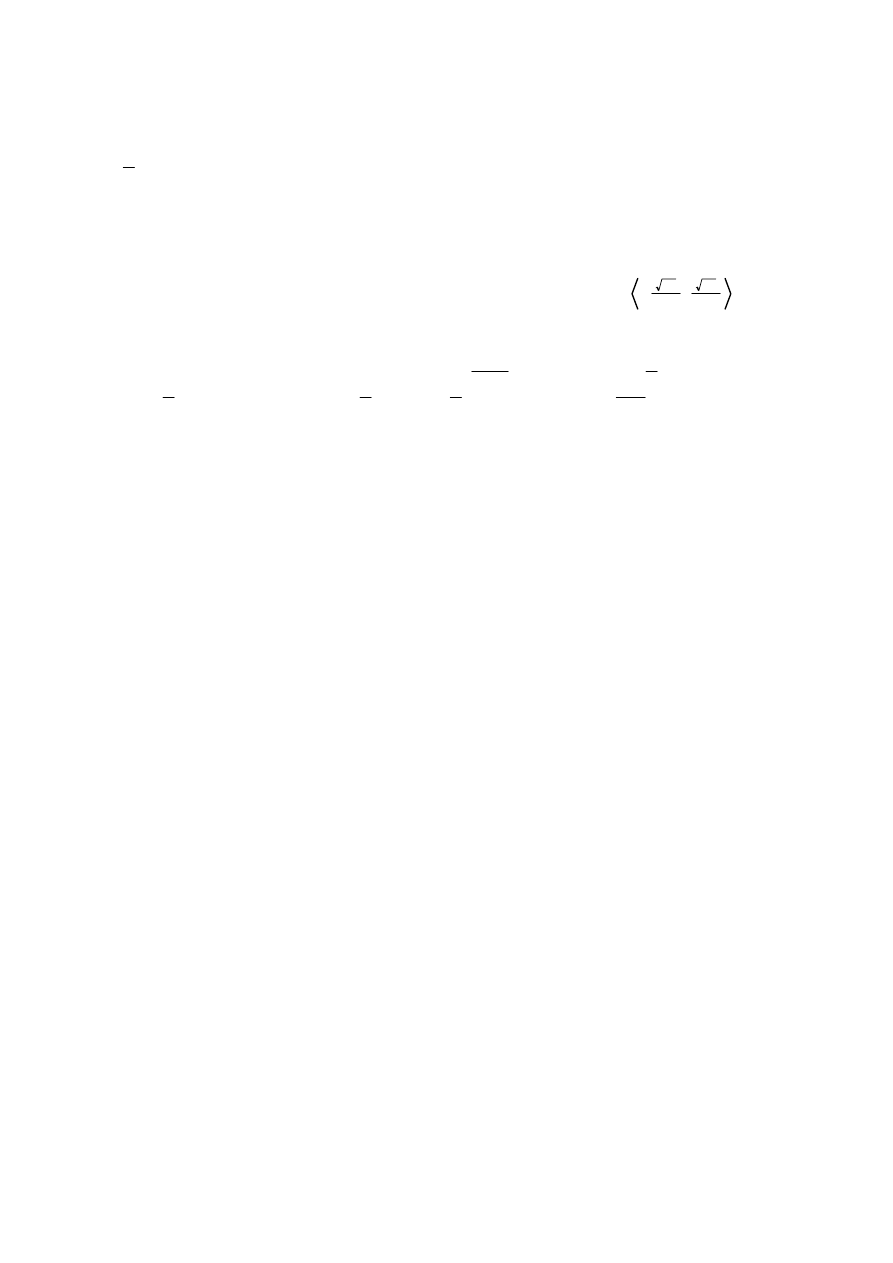
13. Określ obraz i przeciwobraz zbioru A, wyznaczony przez funkcję f:
a) A

 〈−

1
2

, 1

, fx  x

2

 1;

b) A

 〈−1,0, fx  x

2

;

c) A〈0, 1, fx  x

2

.

Odpowiedzi do niektórych zadań:
1a) D

f

: x

∈ −, −5  〈3,;

1b) D

f

: x

∈ −, −2  2, ;

1c) D

f

: x

∈ 2, 3;

1c) D

f

: x

∈ 1, ;

2a) D

f

: x

∈ 〈−2,2, W : y ∈ 〈0,2;

2b) D

f

 3, W  0;

2c) D

f

:

−1, 3;

2d) D

f

 , W : y ∈ 〈5,;

2e) D

f

 , W : y ∈ −

15

30

,

15

30

;

4a) nie;

4b) nie;

4c) nie;

4d) tak;

8a) parzysta;

8b) nieparzysta;

8c) parzysta;

8d) nieparzysta;

8e) parzysta;

8f) nie ma własności parzystości;

8g) nie ma własności parzystości;

11a) f

−1

x 

−dxb

cx

−a

, D

f

−1

: x

∈  ∖ 

a

c

;

11b) f

−1

x 

1
3

10

3x

;

11c) f

−1

x 

1
4

log

2

x

 −

1
4

;

11d) f

−1

x 

x

1

−|x|

.