2. Funkcje charakterystyczne i funkcje stanu
1.23. Obliczyć zmianę entropii azotu o masie m przy ogrzaniu go od temperatury
T
0
do temperatury T, a) izochorycznie, b) izobarycznie.
Rozwiązanie
Na mocy drugiej zasady termodynamiki różniczka zupełna entropii jest równa:
dS
dQ
T
nC dT pdV
T
V
=
=
+
.
Całkując to równanie stronami mamy ogólny związek:
µ
=
⎮
⌡
⌠
+
⎮
⌡
⌠
=
−
m
n
,
T
pdV
T
dT
nC
S
S
V
0
,
gdzie S
0
jest stałą całkowania.
a) Dla przemiany izochorycznej dV = 0 i poprzednie równanie przyjmuje postać:
S S
m
C
dT
T
m
C
T
T
mc
T
T
V
T
T
V
V
−
=
⌠
⌡
⎮
=
=
0
0
0
0
µ
µ
ln
ln
.
b)
Dla przemiany izobarycznej dp = 0, zatem korzystamy z równania stanu:
pV
mRT
=
µ
,
które w postaci różniczkowej przyjmuje postać:
pdV Vdp
mR
dT
+
=
µ
.
Stąd wyznaczamy wielkość pdV przy warunku dp = 0:
pdV
mR
dT
=
µ
.
Podstawiając tę wielkość do równania na zmianę entropii i uwzględniając przy tym związek
Mayera:
C
C
p
V
R
=
+
,
otrzymujemy dla przemiany izobarycznej:
(
)
.
T
T
ln
R
C
m
T
T
ln
R
m
T
T
ln
C
m
T
dT
R
m
T
dT
C
m
S
S
0
V
0
0
V
T
T
T
T
V
0
0
0
+
µ
=
µ
+
µ
=
⎮
⌡
⌠
µ
+
⎮
⌡
⌠
µ
=
−
S S
mc
T
T
p
−
=
0
0
ln
.
1.24. Jak zmieni się entropia wody o masie m
1
i temperaturze T
1
po zmieszaniu jej
z masą m
2
wody o temperaturze T
2
?
Rozwiązanie
Ciepło zawarte w wodzie o masie m
1
i m
2
w danych temperaturach musi być równe
ciepłu wody o masie m
1
+ m
2
, mamy więc równanie bilansu, z którego wyznaczamy
temperaturę wody po zmieszaniu:
(
)
m cT
m cT
m
m cT
T
m T
m T
m
m
1
1
2
2
1
2
1 1
2
2
1
2
+
=
+
⇒
=
+
+
.
Z drugiej strony entropia wody przed zmieszaniem jest równa sumie entropii obu
porcji wody i może być wyrażona zgodnie z całkową postacią drugiej zasady termodynamiki
jak następuje:
0
2
2
0
1
1
T
T
2
T
T
1
T
T
2
T
T
1
1
T
T
ln
c
m
T
T
ln
c
m
T
cdT
m
T
cdT
m
T
dQ
T
dQ
S
2
0
1
0
2
0
1
0
+
=
⎮
⌡
⌠
+
⎮
⌡
⌠
=
⎮
⌡
⌠
+
⎮
⌡
⌠
=
.
Po zmieszaniu analogiczne wyrażenie na entropię przyjmuje postać:
.
T
T
ln
mc
T
mcdT
T
dQ
S
0
T
T
T
T
2
0
0
=
⎮
⌡
⌠
=
⎮
⌡
⌠
=
gdzie m = m
1
+ m
2.
Zmiana entropii w tym procesie wynosi zatem:
0
2
2
0
1
1
0
2
0
1
1
2
T
T
ln
c
m
T
T
ln
c
m
T
T
ln
c
m
T
T
ln
c
m
S
S
S
−
−
+
=
−
=
∆
.
T
T
.
T
T
ln
T
T
ln
c
m
T
T
ln
c
m
ln
c
m
ln
c
m
c
m
2
c
m
1
2
2
1
1
T
T
T
T
2
T
T
T
T
1
2
1
0
2
0
0
1
0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
+
=
+
=
1.25. Udowodnić, że całkowita zmiana entropii gazu doskonałego w cyklu Carnota
równa się zero.
Rozwiązanie
p
1
V
2
4
3
Dla cyklu Carnota przedstawionego na rysunku, mamy cztery następujące po sobie
przemiany gazowe:
1. izotermiczne (T
1
, (1
⇒2)) rozprężanie
2. adiabatyczne ((T
1
⇒
T
2
), (2
⇒3)) rozprężanie
3. izotermiczne (T
2
, (3
⇒4)) sprężanie
4. adiabatyczne ((T
2
⇒
T
1
), (4
⇒1)) sprężanie
Entropia w danym stanie jest określona z dokładnością do stałej. Oznaczając tę stałą
przez S
0
, pełna zmiana entropii w całym cyklu Carnota jest sumą entropii poszczególnych
przemian gazowych:
(
) (
) (
) (
)
S S
S
S
S
S
S
S
S S
−
=
−
+
−
+
−
+
−
0
1
0
2
1
3
2
3
.
1.
1
2
V
V
0
1
V
V
ln
R
m
V
dV
R
m
T
pdV
T
dQ
S
S
2
1
µ
=
⎮
⌡
⌠
µ
=
⎮
⌡
⌠
=
⎮
⌡
⌠
=
−
.
2.
0
dQ
0
T
dQ
S
S
1
2
=
=
=
−
∫
.
3.
3
4
V
V
2
3
V
V
ln
R
m
V
dV
R
m
T
pdV
T
dQ
S
S
4
3
µ
=
⎮
⌡
⌠
µ
=
=
=
−
∫
∫
.
4.
0
dQ
0
T
dQ
S
S
3
=
=
=
−
∫
.
Z drugiej strony dla przemian izotermicznych w tym cyklu, równania stanów
pozwalają wyrazić odpowiednie stosunki objętości przez stosunki ciśnień:
⎪
⎪
⎩
⎪⎪
⎨
⎧
⇒
⇒
.
p
p
=
V
V
const,
=
T
,
V
p
=
V
p
,
p
p
=
V
V
const,
=
T
,
V
p
=
V
p
4
3
3
4
2
3
3
4
4
1
2
2
1
1
2
2
1
1
Podobnie korzystając z równań dla przemian adiabatycznych wchodzących w cykl Carnota
mamy związki:
,
V
V
p
p
V
V
p
p
,
V
p
V
p
,
V
p
V
p
4
3
4
3
1
2
1
2
4
4
1
1
3
3
2
2
χ
χ
κ
κ
χ
χ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⇒
⎪⎩
⎪
⎨
⎧
=
=
1
4
3
1
1
2
4
3
3
4
1
2
2
1
V
V
V
V
,
V
V
V
V
V
V
V
V
−
χ
−
χ
χ
χ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⇒
.
Stąd widać, że:
2
1
3
4
4
3
1
2
V
V
V
V
V
V
V
V
=
⇒
=
.
Podstawiając ten wynik do wzoru na S
3
-S
2
otrzymujemy:
1
2
2
1
2
3
V
V
ln
R
m
V
V
ln
R
m
S
S
µ
−
=
µ
=
−
.
Stąd sumując wszystkie wkłady w całym cyklu Carnota, stwierdzamy, że całkowita zmiana
entropii jest równa zero:
0
0
V
V
ln
R
m
0
V
V
ln
R
m
S
1
2
1
2
=
+
µ
−
+
µ
=
∆
, cbdo.
1.26. W butli o objętości V
1
znajduje się gaz pod ciśnieniem p
1, a w
drugiej butli
o objętości V
2
znajduje się inny gaz pod ciśnieniem p
2
. Temperatury obu gazów są
jednakowe i równe T. Obliczyć jak zmieni się entropia tego gazu po połączeniu obu
butli. (Gazy nie reagują chemicznie!)
Rozwiązanie
Oznaczając przez
∆S
2
zmianę entropii mieszaniny gazów przy przejściu z temperatury
T
0
do temperatury T
2
jaka ustali się po zmieszaniu gazów mamy wyrażenie:
∆S
dQ
T
m
C
dT
T
p dV
T
m
C
dT
T
p dV
T
V
To
T
V
To
T
2
1
1
1
1
2
2
2
2
2
2
=
=
⌠
⌡
⎮
⌠
⌡
⎮
+ ⌠
⌡
⎮
+
⌠
⌡
⎮
+ ⌠
⌡
⎮
µ
µ
( )
( )
.
W całkach nieoznaczonych korzystamy z równania stanu dla każdego z gazów składowych
i wyznaczamy ciśnienia cząstkowe p
1
i p
2
:
,
V
T
R
m
p
,
V
T
R
m
p
2
2
2
1
1
1
µ
=
µ
=
Podstawienie tych związków do poprzedniego równania prowadzi do rezultatu postaci:
,
V
V
ln
R
m
m
T
T
ln
C
m
C
m
V
dV
R
m
m
T
T
ln
C
m
C
m
S
0
2
2
1
1
0
2
)
2
(
V
2
2
)
1
(
V
1
1
V
V
2
2
1
1
0
2
)
2
(
V
2
2
)
1
(
V
1
1
2
0
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
=
⎮
⌡
⌠
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
=
∆
gdzie V = V
1
+ V
2
jest objętością zajmowaną przez mieszaninę.
Oznaczając przez
∆
∆
S
1
i S
2
zmiany entropii poszczególnych gazów przed zmieszaniem przy
przejściu poszczególnych gazów od temperatury T
0
(dowolnej) do temperatury początkowej
tych gazów przed zmieszaniem, całkowita entropia przed zmieszaniem jest równa:
∆
∆
∆
S
S
1
1
=
+ S
2
a poszukiwana zmiana entropii jest równa:
∆
∆
∆
∆
∆
∆
S
S
S
S
S
S
=
−
=
−
−
2
1
2
1
2
,
przy czym zmiany entropii gazów składowych dane są przez wyrażenia tego samego typu co
zmiana entropii mieszaniny, mianowicie:
∆S
m
C
T
T
m
R
V
V
V
1
1
1
1
0
1
1
1
0
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
µ
µ
( )
ln
ln
,
.
V
V
ln
R
m
T
T
ln
C
m
S
0
2
2
2
0
)
2
(
V
2
2
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
=
∆
Stąd poszukiwana zmiana entropii wskutek zmieszania jest równa:
.
V
V
ln
R
m
T
T
ln
C
m
V
V
ln
R
m
T
T
ln
C
m
V
V
ln
R
m
m
T
T
ln
C
m
C
m
S
0
2
2
2
0
)
2
(
V
2
2
0
1
1
1
0
)
1
(
V
1
1
0
2
2
1
1
0
2
)
2
(
V
2
2
)
1
(
V
1
1
⎥
⎦
⎤
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
−
⎥
⎦
⎤
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
µ
+
µ
=
∆
1.27. Pewna ilość gazu doskonałego o objętości V
1 i
ciśnieniu p
1
rozpręża się
w stałej temperaturze T
1
do objętości V
2
. Obliczyć zmianę entropii i energii
swobodnej w tym procesie.
Rozwiązanie
Zmiana entropii dana jest wyrażeniem:
∫
∆S
dQ
T
m
C
T
dT
pdV
T
mR
dV
V
mR
V
V
V
T
T
V
V
=
=
⌠
⌡
⎮
+ ⌠
⌡
⎮
=
⌠
⌡
⎮
=
µ
µ
1
1
1
2
1
1
1
1
2
ln
µ
,
gdzie skorzystano z faktu, ze w przemianie izotermicznej T
1
= const.
Aby
wyliczyć zdefiniowaną w zadaniu zmianę energii swobodnej F skorzystamy
z definicji:
(
)
dF d U TS
dU TdS SdT
=
−
=
−
−
,
przy czym w przemianie izotermicznej dT = 0 i stąd dU = 0. Mamy więc:
dF
TdS
dQ
pdV
= −
= −
= −
.
Całkując to równanie stronami mamy:
∫
1
2
0
V
V
1
V
V
0
V
V
ln
mRT
V
dV
mRT
pdV
F
F
2
1
2
1
µ
−
=
⎮
⌡
⌠
µ
−
=
−
=
−
.
Wykorzystując równanie stanu mamy:
mR
p V
T
µ
=
1
1
1
i szukane wielkości entropii oraz energii swobodnej wyrażają się przez parametry dane
w zadaniu:
∆S
m
R
V
V
p V
T
V
V
=
=
µ
ln
ln
2
1
1
1
1
2
1
,
∆F
m
RT
V
V
p V
V
V
= −
= −
µ
1
2
1
1
1
2
1
ln
ln
.
1.28. Pewną ilość azotu o masie m i temperaturze T
0
sprężono przy stałym
ciśnieniu do 3/4 zajmowanej objętości. Obliczyć jak zmienił się w tym procesie
potencjał termodynamiczny gazu.
Rozwiązanie
Potencjał termodynamiczny G jest funkcją charakterystyczną zależną od potencjałów
P
k
i jest zdefiniowany równaniem ogólnym:
.
x
P
U
G
n
1
k
k
k
∑
=
−
=
W przypadku układu o dwu stopniach swobody (S, V) równanie redukuje się do
postaci:
G = U + pV - TS
.
Różniczka zupełna tego potencjału jest zatem równa:
dG dU pdV Vdp TdS SdT dQ Vdp TdS SdT Vdp SdT
=
+
+
−
−
=
+
−
−
=
−
.
Ponieważ proces jest izobaryczny to dp = 0 i dG redukuje się do postaci:
dG
SdT
= −
.
Całkując to równanie stronami mamy równanie całkowe:
∫
G G
S T dT
−
= −
0
( )
.
Aby wykonać wskazane całkowanie musimy znać zależność entropii od temperatury.
Zależność tę znajdziemy z równania:
(
)
(
)
,
T
T
ln
R
C
m
T
dT
R
C
m
T
pdV
T
dT
C
m
S
T
dQ
S
S
0
V
T
T
V
V
0
0
0
+
µ
=
⎮
⌡
⌠
+
µ
=
+
µ
+
=
⎮
⌡
⌠
+
=
∫
∫
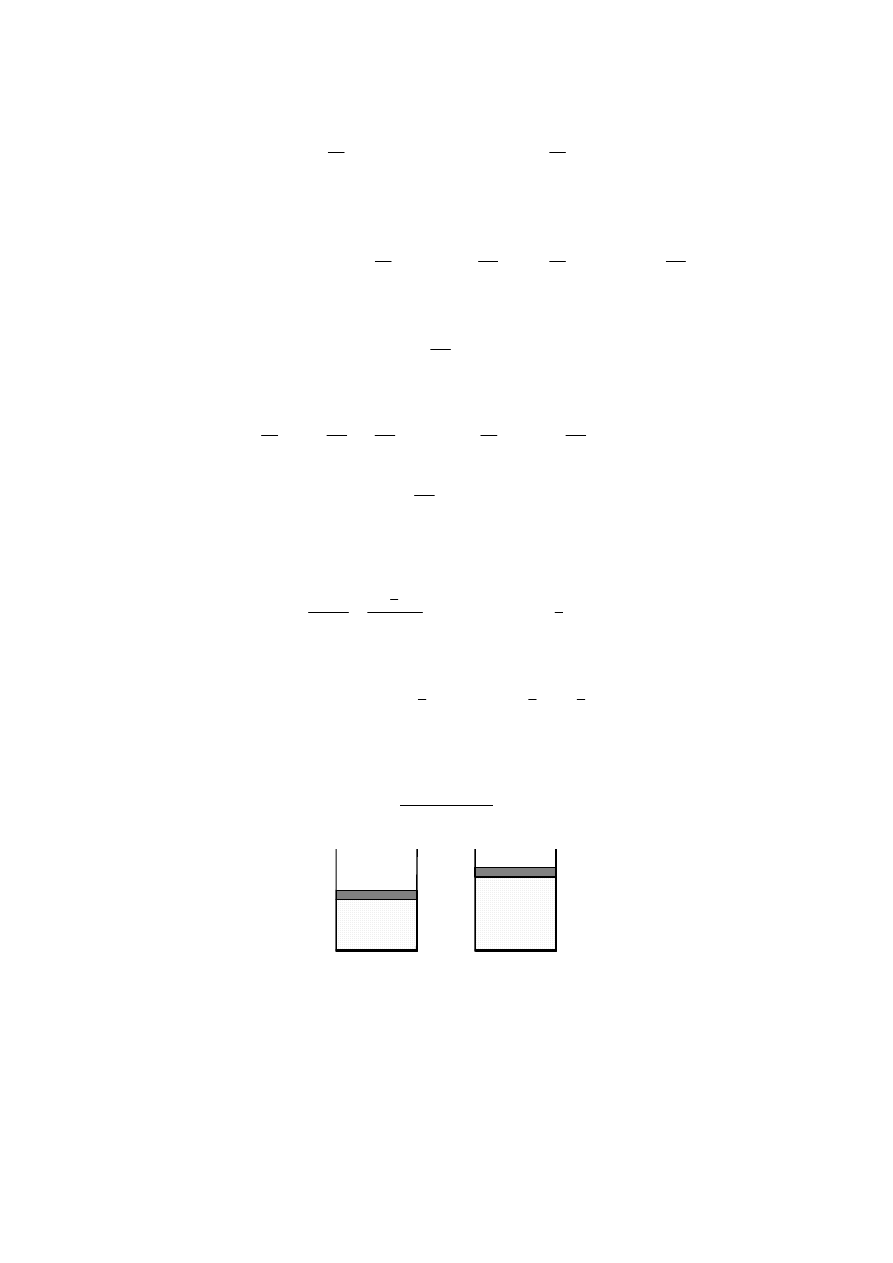
gdzie wykorzystano równania:
pV
m
RT
=
µ
i
pdV
m
RdT
=
µ
.
Podstawiając znalezioną temperaturową zależność do wyrażenia podcałkowego
mamy:
∫
G G
S T dT
−
= −
0
( )
=
(
)
(
)
−
+
⌠
⌡
⎮
= −
+
⌠
⌡
⎮
m
C
R
T
T
dT
m
C
R
T
T
dT
V
V
µ
µ
ln
ln
0
0
.
Wykorzystując znany wzór na całkę z logarytmu naturalnego:
(
)
,
dx
T
dT
,
x
T
T
,
1
x
ln
x
xdx
ln
0
0
=
⇒
=
−
=
∫
otrzymujemy dla potencjału Gibsa wyrażenie:
(
)
(
)
.
T
T
ln
T
mc
T
T
mc
1
1
ln
T
1
T
T
ln
T
C
m
1
T
T
ln
T
T
T
C
m
G
G
0
p
0
p
0
0
p
T
T
0
0
0
p
0
0
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
µ
−
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
µ
−
=
−
Ponieważ z treści zadania wynika, że proces sprężania jest opisany równaniem
stanów, w którym ciśnienie jest stałe a objętość zmniejsza się do trzech czwartych objętości
początkowej, to można wyznaczyć temperaturę końcową T:
p V
T
p
V
T
T
T
0
0
0
0
3
4
0
3
4
0
=
⇒
=
.
W ten sposób zmiana potencjału termodynamicznego Gibsa jest ostatecznie dana
wyrażeniem:
(
)
G G
mc
T
mc
T
p
p
−
=
−
+
0
3
4
0
3
4
0
4
3
1
ln
1.29. Udowodnić, że jeżeli proces zmiany stanu układu gazu pod tłokiem zachodzi
przy stałym ciśnieniu, to ilość wymienianego ciepła jest równa entalpii.
Rozwiązanie
Oznaczmy
przez
∆U = U
2
- U
1
zmianę energii wewnętrznej przy przejściu układu ze
stanu oznaczonego na rysunku symbolem 1 do stanu 2.
dQ
⇒
1
2
Zgodnie z pierwszą zasadą termodynamiki zmiana energii wewnętrznej dU w procesie
infinitezymalnie małym między stanami 1 i 2 jest dana przez:
dU = dQ + dA.
Całkując to równanie otrzymujemy pełną zmianę energii wewnętrznej wyrażoną przez
zmianę objętości:
(
)
∫
U
U
Q p dV Q p V
V
2
1
2
1
−
= −
= −
−
.
Równanie to można również przepisać w bardziej fizycznie dostępnej do interpretacji postaci
odpowiednio grupując wyrazy, mianowicie zapiszmy je w postaci:
U
2
+ pV
2
= U
1
+ pV
1
+ Q.
Z tego równania wyraźnie widać, że entalpia w stanie końcowym jest równa entalpii w stanie
początkowym plus dostarczone ciepło. Możemy zatem określić zmianę entalpii:
(U
2
+ pV
2
)- (U
1
+ pV
1
) = H
2
-H
1
= Q.
Mamy więc równanie wyrażające sens fizyczny entalpii:
H
2
– H
1
= Q.
Zauważmy w tym miejscu, że w procesie izobarycznym, skoro dQ = dH to:
∂
∂
∂
∂
H
T
Q
T
C
p
p
p
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ =
,
C
H
T
p
p
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
,
gdzie C
p
jest pojemnością cieplną rozważanego układu
1.30. Korzystając z
własności układu termodynamicznego składającego się
z dwóch faz rozdzielonych powierzchnią pokazać, że swobodna energia na
jednostkę powierzchni rozdziału faz, jest równa napięciu powierzchniowemu
γ.
Znaleźć dodatkowo wyrażenie na energię wewnętrzną jednostki tej powierzchni.
Rozwiązanie
Przyjmując oznaczenia podane na rysunku, gdzie n oznacza koncentrację cząstek, V
objętość a S entropię danej fazy, wyrażenie na różniczkę energii wewnętrznej obu faz
możemy zapisać jak następuje:
dU TdS p dV
p dV
d
dN
dN
=
− ′
′ − ′′
′′ +
+ ′
′ + ′′
′′
γ σ µ
µ
,
przy czym wielkość
γdσ jest dodatkową energią związaną z występowaniem w układzie
powierzchni. Sama zaś wielkość
γ jest energią jednostki tej powierzchni.
p o w ie r z c h n ia
σ
r o z d z ie la ją c a
fa z y 1 i 2 .
V
′, n ′
T , S
′
V
′′, n ′′
T , S
′′
2
1
Dalej
pełna objętość i liczba cząstek obu faz jest równa:
V
n
V
n
N
V
V
V
′′
′′
+
′
′
=
′′
+
′
=
Energia swobodna F, układu z powierzchnią i energia swobodna hipotetycznego
układu bez tej powierzchni F’ reprezentują dwie różne wielkości. Zapiszemy to stwierdzenie
jak następuje:
(
)
(
)
(
)
F T V V
N N
U TS F
F T V N
F T V N
,
,
, ,
,
'
,
,
,
,
′ ′′
′ ′′ =
−
≠ ≡ ′
′ ′ + ′′
′′
′′
σ
.
Różnica tych dwu wielkości określa właśnie energię swobodną powierzchni:
(
)
F
F
F
F
σ
= − ′ + ′′
.
Mamy zatem wyrażenia na różniczki zupełne zdefiniowanych wyżej energii swobodnych:
(
)
.
N
d
V
d
p
dT
S
F
d
3
,
N
d
V
d
p
dT
S
F
d
2
,
N
d
N
d
d
V
d
p
V
d
p
SdT
SdT
TdS
dU
TS
U
d
dF
1
′′
µ ′′
+
′′
′′
−
′′
−
=
′′
°
′
µ′
+
′
′
−
′
−
=
′
°
′′
µ ′′
+
′
µ′
+
σ
γ
+
′′
′′
−
′
′
−
−
=
−
−
=
−
=
°
Stąd znajdujemy:
(
)
[
]
dF
dF dF
dF
S
S
S
dT
d
σ
γ σ
=
−
′ −
′′ = − − ′ + ′′
+
,
gdzie
oznacza energię swobodną powierzchni.
(
F
F T
σ
σ
σ
=
,
)
Jeżeli wymiary układu przy T = const wzrastają
α
razy, to powierzchnia zmieni się
α razy, wtedy:
(
)
( )
F T
F T
σ
σ
ασ
α
σ
,
,
=
.
Różniczkując to równanie po
α otrzymujemy równania na energię swobodną
i entropię:
T
T
F
S
,
F
F
∂
∂γ
σ
−
=
∂
∂
−
=
γ
⋅
σ
=
∂σ
∂
σ
=
σ
σ
σ
σ
Przy pomocy tych równań energia wewnętrzna powierzchni daje się zapisać jak następuje:
U
F
TS
T
T
T
T
σ
σ
σ
γσ
σ
∂γ
∂
γ
∂γ
∂
σ
=
+
=
+
−
⎛
⎝⎜
⎞
⎠⎟
=
−
⎛
⎝⎜
⎞
⎠⎟
.
Stąd energia wewnętrzna przypadająca na jednostkę powierzchni jest równa:
U
T
T
σ
σ
γ
∂γ
∂
= −
.
1.31. Znaleźć formułę dla obliczania potencjału Gibsa G, entalpii H i entropii S,
przy pomocy współczynników eksperymentalnych A(T), B(T), C(T), ... rozkładu
równania stanu: p
V
=
A(T) + B(T)p
+ C(T)p
2
+....
Rozwiązanie
Zgodnie z definicją potencjału termodynamicznego Gibsa G:
G = U - TS + p V
różniczka zupełna tej wielkości jest równa:
SdT+Vdp
p=
SdT+pdV+Vd
TdS
pdV
dG=TdS
−
−
−
−
.
Stąd:
V
p
G
V
dp
dT
S
dp
dG
const
T
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⇒
+
−
=
=
Podstawiając do tego równania w miejsce V rozwinięcie wirialne dane w treści zadania,
mamy:
( )
( )
( )
( )
( ) ( )
L
L
+
+
+
=
+
⋅
+
⋅
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
p
T
C
T
B
p
T
A
p
p
T
C
p
p
T
B
p
T
A
p
G
2
const
T
Całkując teraz otrzymane równanie po p dostajemy:
( )
( ) ( )
.
dp
p
T
C
T
B
p
T
A
dp
p
G
const
T
⎮
⌡
⌠
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
=
⎮
⌡
⌠
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
L
Oznaczając przez p
0 i
p ciśnienie początkowe i końcowe, po wykonaniu całkowania
w tych granicach otrzymujemy formułę na potencjał termodynamiczny Gibsa:
( )
(
)
( )
( )(
)
( )
(
)
.
p
p
2
T
C
p
p
T
B
p
p
ln
T
A
p
,
T
G
p
,
T
G
2
0
2
0
0
0
L
+
−
+
−
+
=
−
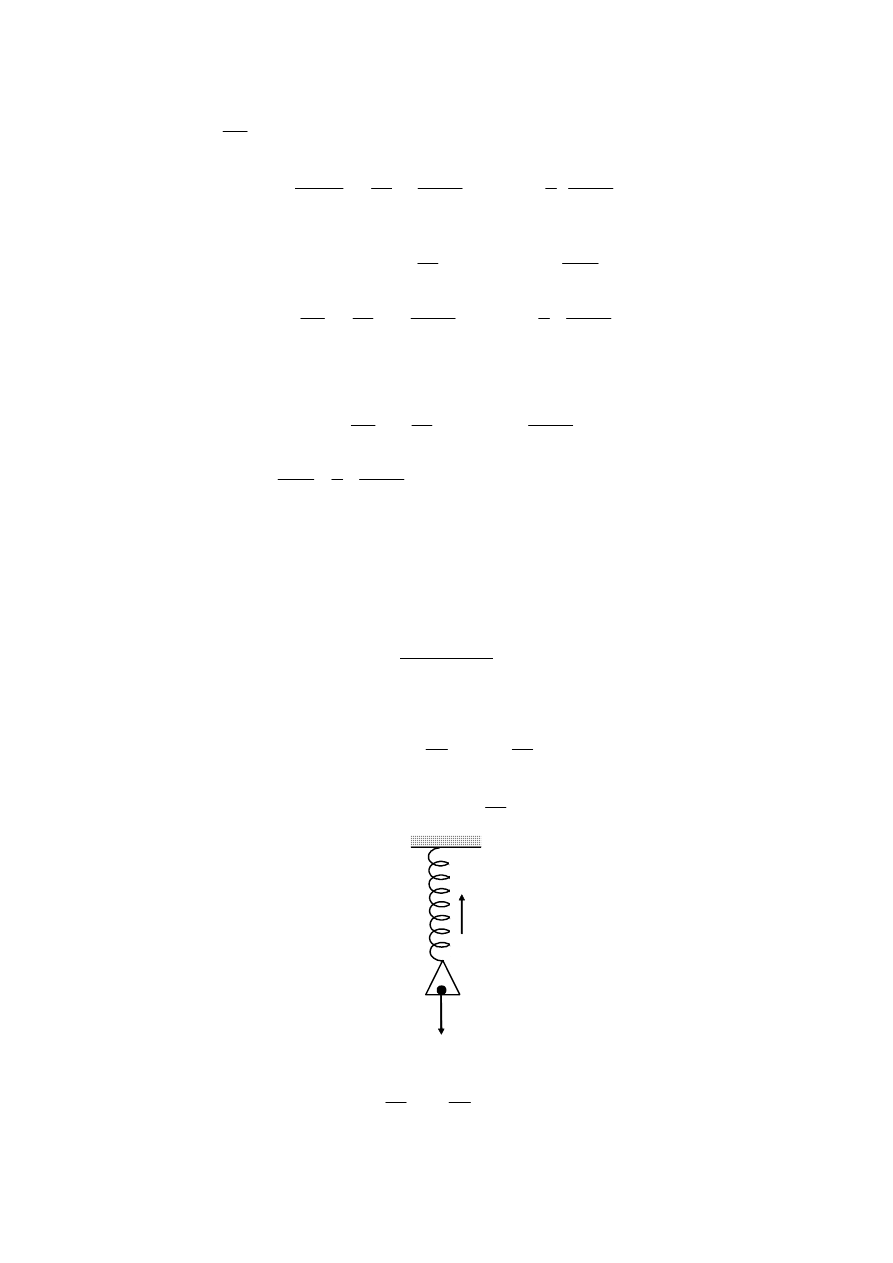
Formułę na entropię otrzymamy przy pomocy znalezionego potencjału i związku
Maxwella na entropię, tj. z równania:
(
)
( )
( )
(
)
.
p
p
T
T
C
2
1
)
p
p
(
T
T
B
p
p
ln
T
)
T
(
A
p
,
T
S
T
G
S
2
0
2
0
0
0
p
L
+
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
Ostatnią wielkość tj. entalpię znajdujemy z definicji tej wielkości:
(
)
( )
( )(
)
( )
(
)
(
)
( )
( )
(
)
.
p
p
T
T
C
T
2
1
)
p
p
(
T
T
B
T
p
p
ln
T
A
T
T,p
TS
p
p
2
T
C
p
p
T
B
p
p
ln
T
A
p
,
T
G
TS
G
H
2
0
2
0
0
0
2
0
2
0
0
0
L
L
+
−
∂
∂
−
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
−
+
−
+
−
+
+
=
+
=
Grupując odpowiednie wyrazy razem otrzymujemy ostatecznie:
(
)
(
)
[
]
( )
( )
( ) (
)
( )
( )
(
)
......
p
p
T
T
C
T
2
1
2
T
C
p
p
T
T
B
T
T
B
p
p
ln
T
A
T
T
A
p
,
T
S
T
p
,
T
G
H
2
0
2
0
0
0
0
+
−
⎥⎦
⎤
⎢⎣
⎡
∂
∂
−
+
+
−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
+
−
=
1.32. Dany jest układ składający się ze sprężyny podlegającej prawu Hooke’a, przy
czym stała siłowa sprężyny, zależy od temperatury. Znaleźć energię swobodną,
energię wewnętrzną i
entropię jako funkcje wydłużenia sprężyny x.
Rozszerzalności nie uwzględniać.
Rozwiązanie
Oznaczając przez x wydłużenie sprężyny, różniczkę zupełną energii swobodnej
danego układu termodynamicznego zapiszemy jak następuje:
(
)
( )
dF d U TS
dF T x
F
T
dT
F
x
dx
SdT Xdx
x
T
=
−
=
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
= −
+
,
∂
∂
∂
∂
,
gdzie siła uogólniona X dana jest równaniem: X
F
x
T
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
X
X
Z poprzedniego równania pochodna zupełna energii swobodnej po wydłużeniu sprężyny jest
równa:
dF
dx
S
dT
dx
X
= −
+
.
Dla procesu izotermicznego gdy dT = 0 otrzymujemy:
( )
∂
∂
F
x
X
dF T x
dx
kx
T const
T const
⎛
⎝⎜
⎞
⎠⎟
=
=
=
=
=
;
.
Całkując to ostatnie równanie znajdujemy wyrażenie na energię swobodną jako funkcję
wydłużenia sprężyny:
( )
( )
( )
T
2
T
2
1
k
T
k
k
,
x
k
0
,
T
F
x
,
T
F
=
=
+
=
.
Entropię układu znajdziemy różniczkując energię swobodną po temperaturze przy stałym
wydłużeniu:
( )
( )
( )
S T x
F
T
F T
T
k
T
x
S T
k x
x
x
x
,
,
,
= −⎛
⎝⎜
⎞
⎠⎟
= −
⎛
⎝
⎜
⎞
⎠
⎟ − ⎛
⎝⎜
⎞
⎠⎟
=
−
′ ⋅
∂
∂
∂
∂
∂
∂
0
1
2
0
2
1
2
2
,
.
T
k
k
x
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
′
Dalej z definicji energii swobodnej wyliczymy energię wewnętrzną:
( )
{
}
( )
(
)
( )
( )
{
} (
)
( ) (
)
.
x
T
'
k
k
0
,
T
U
x
T
'
k
k
0
,
T
TS
0
,
T
F
x
'
k
0
,
T
S
T
kx
0
,
T
F
TS
F
U
2
2
1
2
2
1
2
2
1
2
2
1
−
+
=
⋅
−
+
+
=
⋅
−
+
+
=
+
=
1.33. Rozwiązać poprzednie zadanie, posługując się energią swobodną układu
F
*
(T, x) = F(T, x)-Xx. w szczególności określić sens fizyczny energii swobodnej
i różniczki energii swobodnej.
Rozwiązanie
Z
o
M
X
t
X
X
u
Siły zewnętrzne, w tym przypadku siły grawitacji, równoważą w stanie równowagi siły
wewnętrzne sprężystości co schematycznie przedstawiono na rysunku wyżej.
Na rysunku niżej przedstawiono zmianę stanu termodynamicznego 1 w 2
spowodowaną położeniem na szalkę masy M znajdującej się wcześniej na poziomie
pierwotnym równowagi układu z
0
1
⇒ 2
M
x
Z
o
Z
o
M
M’
x
M’
Wykonajmy nad układem następujący eksperyment myślowy polegający na przeniesieniu
masy M z jej pierwotnego położenia na szalkę, co spowoduje proces termodynamiczny
wydłużenia sprężyny.
Pełna energia potencjalna układu wtedy wynosi:
E
p
= M
′ g Z
o
+ Mg(Z
o
- x) = -M g x + (M + M’) g Z
o
= -X x + const.
Swobodna energia układu zaś będzie równa:
F
*
(T, x) = F(T, x) - X x = F + w + const,
gdzie w = -Xx jest pracą wykonaną przez siły zewnętrzne nad układem.
Z drugiej strony X = k x, skąd wyrażenie na energię swobodną może być zapisane
równaniem:
F = F(T, 0) +
1
2
2
kx
.
Swobodna energia układu sprężyna + odważniki jest więc równa:
( )
( )
F
F T
kx
Xx
F T
X
k
*
,
,
=
+
−
=
−
0
0
1
2
1
2
2
2
.
Stąd różniczka zupełna tej wielkości przyjmuje postać:
( )
(
)
(
)
(
)
x
X
d
kx
d
)
0
,
T
(
dF
dEp
kx
d
)
0
,
T
(
dF
xdX
Xdx
kxdx
0
,
T
dF
dF
2
2
1
2
2
1
*
⋅
−
+
=
+
+
=
−
−
+
=
( )
(
)
dF
dF T
d kx
X x
*
,
=
+
−
0
1
2
2
⋅
,
gdzie wielkość:
(
d kx
X x
1
2
2
− ⋅
)
jest zmianą energii potencjalnej rozciągniętej sprężyny, czyli
pracą wykonaną po niezamocowanym stopniu swobody, jakim jest w tym przypadku długość
sprężyny.
1.34. Udowodnić twierdzenie: Entalpia układu termodynamicznego jest równa
sumie energii wewnętrznej i „źródła pracy”, którą to źródło wykonuje nad
układem.
Rozwiązanie
z
dM
Mg
M
z
x
U
Weźmy pod uwagę układ termodynamiczny gazu pod tłokiem obciążonym masą M,
przedstawiony na rysunku.
Ciśnienie zewnętrzne p
t
(wywierane przez termostat)w stanie równowagi gazu jest równe
ciśnieniu układu p
u
.
Oznaczmy przez
σ pole powierzchni tłoka, a przez
m - masę tłoka.
Ciężarek masy M położonej na tłok wywiera na gaz ciśnienie:
p
p
p
Mg mg
t
u
=
=
=
+
σ
.
Stąd różniczka zupełna tego ciśnienia jest równa:
dp
g
dM
=
σ
.
Źródłem sił zewnętrznych jest ciało o masie M położone na tłok a objętość gazu pod tłokiem
wynosi:
V =
σ⋅z.
Energia potencjalna ciała o masie M położonego na tłoku (energia potencjalna
termostatu U
t
) jest równa:
U
t
= M g z,
podczas gdy energia potencjalna tłoka ma wartość:
U
tłoka
= m g z.
Różniczka zupełna energii wewnętrznej układu (gaz + tłok + ciężarek) dana jest zatem przez
formułę:
dU
*
= dU + dU
t
= dU + d(M g z) = d(U + M g z)
= d(U + p
σz) = d(U + p V),
która stwierdza, że infinitezymalnie mała zmiana energii wewnętrznej układu jest równa
infinitezymalnie małej zmianie entalpii:
dU
*
= dH.
Połóżmy dodatkowo masę dM na tłok, przenosząc ją z pierwotnego położenia jak na rysunku.
Wtedy wykonana praca sił zewnętrznych jest równa:
(
)
( )
dM g z dz
gzdM
g z
dM
z dp
Vdp
⋅
+
≈
=
=
=
σ
σ
σ
,
dU
d U pV
dU pdV Vdp
*
(
)
=
+
=
+
+
.
Widać więc, że wielkość V dp = g z dM jest energią potencjalną masy dM.
1.35. Wykazać, że dla jednorodnego magnetyka pojemność cieplną układu
w stałym polu magnetycznym H można zapisać w
postaci:
C
H
H
H
U
T
H
M
T
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
∂
∂
∂
∂
.Zmianę objętości magnetyka przy magnesowaniu
zaniedbać.
Rozwiązanie
Startujemy z drugiej zasady termodynamiki zapisanej dla układu o dwu stopniach
swobody, przy czym drugi stopień swobody opisuje proces termodynamiczny magnesowania
przy pomocy zmiennej niezależnej M (namagnesowanie) i potencjału termodynamicznego H
(pole magnetyczne magnesujące układ):
dQ dU dA
dU HdM
=
−
=
−
.
Traktując energię wewnętrzną i namagnesowanie rozważanego układu jako funkcje
temperatury i natężenia pola magnetycznego:
(
)
U
U H T
=
,
,
(
)
M
M H T
=
,
, różniczki zupełne
tych funkcji przyjmują formę:
dH.
H
M
dT
T
M
dM
,
dH
H
U
dT
T
U
dU
T
H
T
H
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Podstawiając te wyrażenia do równania na dQ, mamy
dQ =
dT +
∂
∂
∂
∂
∂
∂
∂
∂
U
T
H
M
T
U
H
H
M
H
dH
H
H
T
T
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
.
Przy pomocy tego wyrażenia, przy H = const, pojemność cieplna tego układu z definicji jest
równa:
C
dQ
dT
U
T
H
M
T
H
H
H
H
= ⎛
⎝⎜
⎞
⎠⎟
=
⎛
⎝
⎜
⎞
⎠
⎟ −
⎛
⎝
⎜
⎞
⎠
⎟
∂
∂
∂
∂
,
cbdw.
1.36. Pokazać, że różniczkowa postać dla pracy pdV nie jest różniczką zupełną.
Rozwiązanie
Założymy, dW = pdV jest różniczką zupełną. Oznacza to, że ogólne wyrażenie
różniczkowe na pracę:
dW pdV Xdx
pdV
dT
pdV
dp
=
+
=
+
+
⎧
⎨
⎩
0
0
musi spełniać warunek:
∂
∂
∂
∂
p
x
X
V
V
x
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
.
Ponieważ w wyrażeniu różniczkowym na pracę dla X = 0, dx może oznaczać zarówno dT jak
i dp to otrzymujemy sprzeczność, gdyż dla x = p:
∂
∂
p
p
V
⎛
⎝
⎜
⎞
⎠
⎟ = 1
.
Tymczasem z poprzedniego równania wynika, że
∂
∂
∂
∂
p
x
X
V
V
x
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
= 0 bo X = 0.
Dlatego też đW = pdV nie jest różniczką zupełną.
1.37. Z definicji wielkości U, F, H i G, jako funkcji charakterystycznych (dla
dwóch stopni swobody) pokazać
słuszność następujących związków
termodynamicznych:
,
S
p
V
T
1
V
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
°
,
S
V
p
T
2
p
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
°
,
S
p
V
T
3
T
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
°
.
S
V
p
T
4
T
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
°
Rozwiązanie
Korzystamy ze związku typu:
dz(x, y) = M(x, y)dx + N(x, y)dy,
z którego dla różniczki zupełnej odpowiedniej funkcji charakterystycznej z(x, y) tj. funkcji
stanu, z których każda spełnia związek:
∂
∂
∂
∂
M
y
N
x
x
y
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝⎜
⎞
⎠⎟
znajdujemy kolejne związki podane do udowodnienia:
(
)
.
S
p
V
T
,
pdV
TdS
dU
,
V
,
S
U
U
V
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⇒
=
(
)
.
S
V
p
T
,
Vdp
TdS
Vdp
pdV
pdV
TdS
pV
U
d
dH
p
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
=
+
+
−
=
+
=
(
)
.
S
p
V
T
p
S
T
V
,
SdT
Vdp
SdT
TdS
dH
pV
TS
U
d
dG
T
p
T
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
−
−
=
+
−
=
.
S
V
p
T
V
S
T
p
,
SdT
pdV
dF
S
T
U
F
T
V
T
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
−
=
⇒
⋅
−
=
1.38. Znaleźć zależność między pojemnością cieplną w stałej objętości i przy stałym
ciśnieniu.
Rozwiązanie
Biorąc pod uwagę pierwszą zasadę termodynamiki i definicję różniczki zupełnej
energii wewnętrznej wyrażenie na ciepło w procesie elementarnym można zapisać kolejno jak
następuje:
.
dV
p
V
U
dT
C
dV
p
V
U
dT
T
U
pdV
dU
dQ
T
V
T
V
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
+
=
dQ C dT
T
S
V
p p dV
V
T
=
+
⎛
⎝⎜
⎞
⎠⎟
− +
⎡
⎣
⎢
⎤
⎦
⎥
∂
∂
,
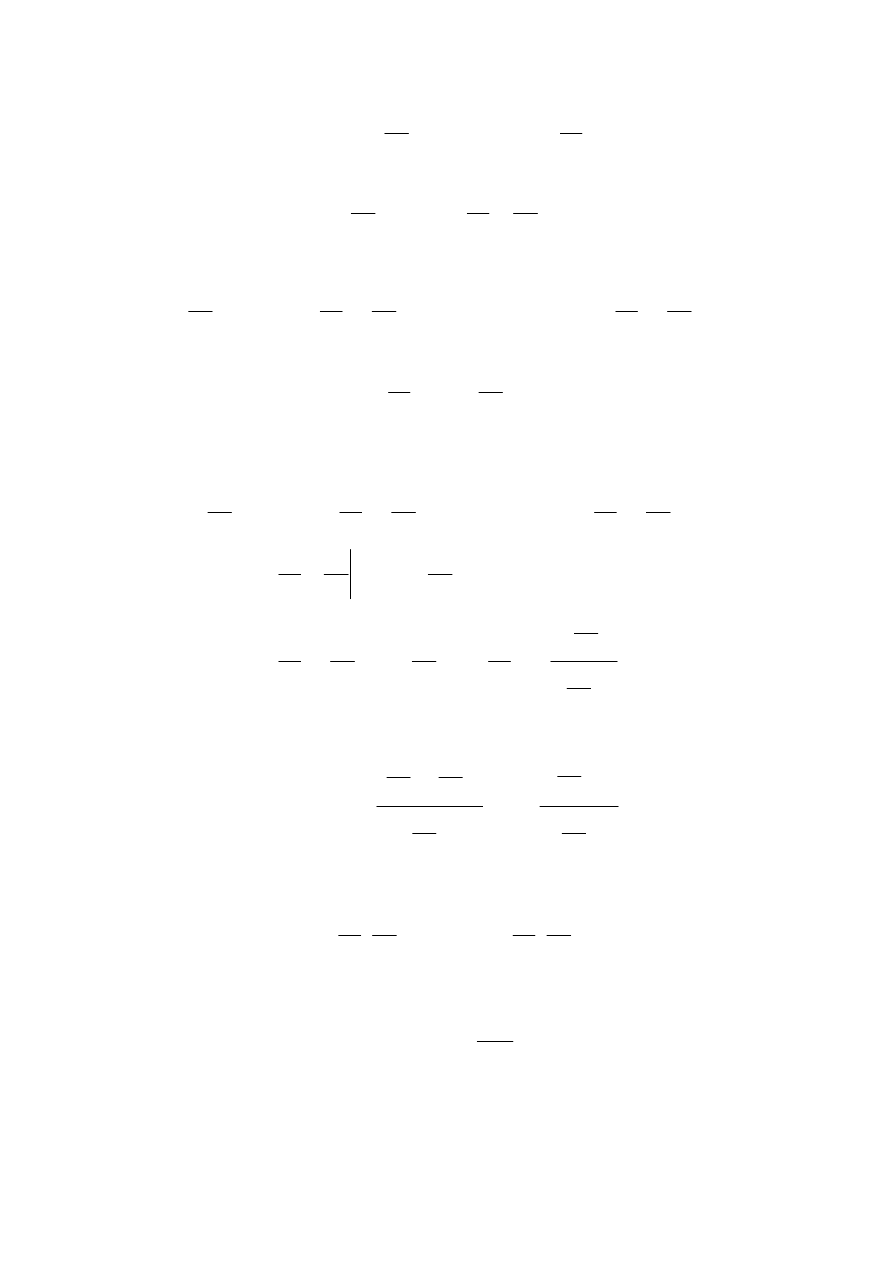
dQ C dT T
S
V
dV C dT T
p
T
dV
V
T
V
V
=
+ ⎛
⎝⎜
⎞
⎠⎟
=
+ ⋅ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Ciepło na jednostkę temperatury, czyli pojemność układu jest zatem równa:
dQ
dT
C
T
p
T
dV
dT
V
V
=
+ ⋅ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Podczas, gdy oddziaływanie układu z termostatem, zachodzi w warunkach stałego ciśnienia
(p = const), możemy wyznaczyć różnicę C
p
-C
V
:
.
T
V
T
p
T
C
C
,
T
V
T
p
T
C
T
Q
p
V
V
p
p
V
V
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
−
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Dalej pisząc równanie stanu w postaci p = p(T, V) określamy różniczkę ciśnienia:
dp
p
T
dT
p
V
dV
V
T
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Dla warunków dp = 0 to ostatnie równanie pozwala wyznaczyć iloczyn pochodnych stojący
w znalezionym wyrażeniu na różnicę pojemności cieplnych dla p = const i V = const,
mianowicie:
,
T
V
T
p
T
C
C
,
T
V
T
p
T
C
T
Q
p
V
V
p
p
V
V
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
−
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
+
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
p
V
T
V
T
p
T
V
p
V
T
p
,
V
p
dV
dT
T
p
T
p
V
p
T
V
T
const
p
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Stąd szukany związek można przekształcić do postaci:
C
C
T
V
T
V
T
V
p
T
V
T
V
p
p
V
p
p
T
p
T
−
= −
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎞
⎠
⎟
⋅ = − ⋅
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎛
⎝
⎜
⎞
⎠
⎟
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
2
.
Zauważmy, że w liczniku i mianowniku stoją współczynniki rozszerzalności izobarycznej
i ściśliwości izotermicznej odpowiednio, zdefiniowane wyrażeniami:
,
p
V
V
1
,
T
V
V
1
T
0
T
p
0
p
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
−
=
β
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
α
gdzie
α
p
-współczynnik rozszerzalności termicznej, a
β
T
-współczynnik ściśliwości
izotermicznej. Stąd ostatecznie mamy znany wzór:
C
C
T
V
p
V
p
T
−
= ⋅
α
β
2
.
1.39. Obliczyć energię swobodną F oraz znaleźć równanie stanu układu, jeżeli
entropia układu jest określona równaniem:
n
0
0
T
T
V
V
R
S
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
, gdzie V
0
, T
0
, i n są
stałymi.
Rozwiązanie
Mamy:
dF = d(U - TS) = - pdV - S dT.
Dla procesu izochorycznego dV = 0 i wtedy
dF = -S dT,
⇒
.
T
F
S
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Całkując to równanie stronami mamy:
(
)
(
)
.
T
T
1
V
1
n
T
RV
T
T
1
n
1
T
1
V
V
R
dT
T
T
1
V
V
R
dT
T
T
V
V
R
SdT
F
1
n
0
0
0
1
n
0
1
n
n
0
0
T
T
n
n
0
0
T
T
n
0
0
T
T
0
0
0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
=
−
+
−
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
=
+
+
+
∫
∫
∫
Z drugiej strony z równania:
dF = - pdV - S dT.
wynika związek:
p
F
V
T
= −⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Zatem różniczkując znalezione wyrażenie na energię swobodną po objętości otrzymujemy
szukane równanie stanu:
(
)
(
)
p
F
V
RV T
n
T
T
V V
RV T
n
T
T
V
T
n
n
= −⎛
⎝⎜
⎞
⎠⎟
=
+
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎛
⎝⎜
⎞
⎠⎟
=
+
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
+
∂
∂
∂
∂
0 0
0
1
0 0
0
1
2
1
1
1
1
1
1
.
1.40. Zgodnie z drugą zasadą „termodynamiki” różniczka zupełna entropii jest
równa dS
dQ
T
=
. Pokazać, że a) dla dowolnego procesu
( ) ( )
dQ
T
S B
S A
A
B
⌠
⌡
⎮
≤
−
; b) dla
izolowanego cieplnie układu entropia nigdy nie maleje.
Rozwiązanie
Z twierdzenia Clausiusa wiemy, że:
dQ
T
∫
≤ 0
R
I
B
A
a) Rozważając proces po drodze R odwracalny i nieodwracalny po drodze i przeprowadzający
układ ze stanu a do stanu B.
Dla procesu odwracalnego R:
∫
0
dS
,
T
dQ
dS
ABA
B
A
B
A
=
≡
∫
∫
,
∫
∫
∫
dS =
ABA
dS
dS
A
B
B
A
+
= 0
.
Stąd mamy:
( ) ( )
.
A
S
B
S
T
dQ
T
dQ
,
0
T
dQ
T
dQ
R
I
R
I
−
⎮
⌡
⌠
≡
≤
⎮
⌡
⌠
⇒
≤
−
∫
∫
b) dQ = 0. z poprzedniego wynika dla procesu adiabatycznego dQ = 0, że:
( ) ( )
0
≤
−
S B
S A
a to oznacza, że dla układu izolowanego entropia nigdy nie maleje.
1.41. Pokazać, że energia wewnętrzna gazu doskonałego nie zależy ani od objętości
V, ani od ciśnienia p; zatem jest funkcją tylko temperatury.
Rozwiązanie
Z uogólnionej pierwszej zasady termodynamiki wyrażenia na różniczkę zupełną
energii wewnętrznej mają postać:
dU
U
S
dS
U
V
dV
dU TdS pdV
V
S
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
=
−
∂
∂
∂
∂
;
.
Pochodna cząstkowa tej energii po objętości przy stałej temperaturze jest równa:
.
p
T
p
T
p
V
S
T
V
U
p
dV
dS
T
dV
dU
V
T
T
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
−
=
Ponieważ z równania stanu gazu doskonałego wynika, że:
p
RT
V
p
T
R
V
V
=
⇒
⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
,
to stwierdzamy, że energia nie zależy od objętości, ponieważ:
∂
∂
U
V
T
R
V
p
T
⎛
⎝⎜
⎞
⎠⎟
= ⋅
− = 0
.
Korzystamy z tego rezultatu rozszerzając pochodną cząstkową energii wewnętrznej po
ciśnieniu i otrzymujemy drugi szukany rezultat, mianowicie:
∂
∂
∂
∂
∂
∂
∂
∂
U
p
U
V
V
p
U
p
T
T
T
T
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝
⎜
⎞
⎠
⎟ ⋅ =
0 0
.
Energia wewnętrzna gazu doskonałego nie zależy od ciśnienia, jest zatem funkcją
temperatury U = U(T).
1.42. Udowodnić związki termodynamiczne:
,
T
p
T
V
C
1
V
2
2
T
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
°
.
T
V
T
p
C
2
p
2
2
T
p
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
°
Rozwiązanie
Korzystamy z definicji pojemności cieplnej układu w stałej objętości, którą można
zapisać przy pomocy równoważnych formuł różniczkowych:
V
V
V
V
T
S
T
T
Q
T
U
C
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
Różniczkując to ostatnie równanie po objętości dla układu w warunkach stałej temperatury
mamy kolejno następujące związki prowadzące do rezultatu, który należało wykazać
w punkcie 1
0
:
,
T
p
T
T
p
T
V
S
T
T
T
S
T
V
V
C
V
2
2
V
V
T
T
V
T
V
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
gdzie skorzystano ze związku Maxwella:
∂
∂
∂
∂
S
V
p
T
T
V
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
.
Analogicznie postępując z pojemnością układu w stałym ciśnieniu, mamy:
.
T
V
T
T
V
T
T
p
S
T
T
T
S
p
T
T
S
T
p
p
C
2
2
p
p
p
T
T
p
T
p
T
p
∂
∂
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
∂
∂
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
W tym przypadku po zamianie kolejności różniczkowania należało skorzystać ze związku
Maxwella:
p
T
T
V
p
S
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
.
1.43. Pokazać, że dla układu, którego energia wewnętrzna jest funkcją tylko
temperatury, równanie stanu ma postać: p = T
⋅ f(V), gdzie f(V) jest pewną funkcją
objętości V tego układu.
Rozwiązanie
Z
założenia treści zadania, że energia wewnętrzna jest funkcją tylko jednego
parametru T, tj. U = U(T) i definicji pojemności cieplnej układu, wynika również
temperaturowa zależność tej ostatniej wielkości:
( )
C
U
T
C T
V
V
V
= ⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
.
Różniczkując tę wielkość po objętości w warunkach stałej temperatury układu otrzymujemy
podobnie jak w poprzednim zadaniu rezultat, który stwierdza, że pojemność cieplna tego
układu zależy od objętości tylko wtedy, gdy ciśnienie jest conajmniej kwadratową funkcją
temperatury
.
0
T
p
T
V
C
V
2
2
T
V
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Biorąc pod uwagę tę ostatnią równość, całkując ją obustronnie otrzymujemy równanie
pierwszego rzędu:
),
V
(
f
dT
dp
,
0
T
p
d
2
2
=
⇒
=
∂
gdzie f = f(V) jest stałą całkowania zależną od objętości ponieważ druga pochodna była brana
przy stałej objętości. Rozdzielając zmienne i całkując ponownie otrzymane równanie
otrzymujemy:
dp f V dT
p f V T f
=
⋅
⇒ =
⋅ +
( )
( )
0
cbdw.
1.44. Udowodnić związek.:
∂
∂
∂
∂
S
V
p
T
T
V
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
Rozwiązanie
Korzystając z definicji energii swobodnej F = U -TS dla różniczki zupełnej tej
wielkości otrzymujemy:
pdV
SdT
dF
−
−
=
skąd widać, ze entropia i ciśnienie są określone przez odpowiednie pochodne cząstkowe
energii swobodnej po temperaturze i objętości układu:
S
F
T
i
p
F
V
V
T
= −⎛
⎝⎜
⎞
⎠⎟
= −⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Różniczkując pierwszy związek po objętości V przy stałej temperaturze T mamy kolejno
wyrażenia:
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
S
V
V
F
T
T
F
V
T
p
T
V
T
T
V
V
⎛
⎝⎜
⎞
⎠⎟
= −
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥ =
⎛
⎝⎜
⎞
⎠⎟
,
gdzie skorzystano po drodze ze zmiany kolejności różniczkowania i definicji ciśnienia.
Mamy zatem związek:
∂
∂
∂
∂
S
V
p
T
T
V
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
,
który należało udowodnić.
1.45. Posługując się związkami termodynamicznymi dla pochodnych cząstkowych
udowodnić, że
∂
∂
∂
∂
p
V
p
V
S
T
⎛
⎝⎜
⎞
⎠⎟
> ⎛
⎝⎜
⎞
⎠⎟
.
Rozwiązanie
Startując z podstawowych definicji potencjałów, jako zmiennych zależnych, od
zmiennych niezależnych S, V dla układu o dwu stopniach swobody mamy układ równań:
( )
( )
p p S V
T T S V
=
=
⎫
⎬
⎪
⎭⎪
,
,
Rozwiązując te równania względem entropii otrzymujemy dwa równania na tę
wielkość:
(
)
( )
S S T V
S S T p
=
=
⎧
⎨
⎩
,
,
Dla tak określonych entropii różniczki zupełne są równe:
.
dp
T
V
dT
T
C
dp
p
S
dT
T
S
dS
,
dV
T
p
dT
T
C
dV
V
S
dT
T
S
dS
p
p
T
p
V
V
T
V
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Ponieważ w przemianie adiabatycznej dS = 0 ostatni układ równań może być przekształcony
do postaci:
⎪
⎪
⎩
⎪⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
.
dp
T
V
C
1
T
dT
,
dV
T
p
C
1
T
dT
p
p
V
V
Przyrównując do siebie prawe strony tych równań mamy wyrażenie na pochodną cząstkową
objętości po temperaturze przy stałym ciśnieniu:
∂
∂
∂
∂
∂
∂
V
T
C
C
p
T
V
p
p
p
V
V
S const
⎛
⎝⎜
⎞
⎠⎟
= −
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎞
⎠
⎟
=
.
Wprowadzając stałą
χ oraz przekształcając to równanie do postaci na wielkość
∂
∂
p
V
S
⎛
⎝⎜
⎞
⎠⎟
mamy:
.
V
T
T
p
V
p
,
p
V
T
p
T
V
p
V
S
S
V
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
χ
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
χ
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Korzystając dalej z równania stanu wyrażającego ciśnienie w funkcji pozostałych parametrów
dla układu o dwu stopniach swobody dostajemy wyrażenie na różniczkę zupełną ciśnienia:
(
)
dp T V
p
T
dT
p
V
dV
V
T
,
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
.
Dla procesu izobarycznego dp = 0 i równanie przyjmuje formę:
∂
∂
∂
∂
∂
∂
p
T
T
V
p
V
V
p
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
= −⎛
⎝⎜
⎞
⎠⎟
T
.
Podstawienie tego wyrażenia do otrzymanego na wielkość
∂
∂
p
V
S
⎛
⎝⎜
⎞
⎠⎟
prowadzi do równości:
∂
∂
χ
∂
∂
p
V
p
V
S
T
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
.
Ponieważ,
χ jest większe od jedności a potencjał termodynamiczny spełnia kryterium
stabilności:
∂
∂
P
x
k
k
S
⎛
⎝
⎜
⎞
⎠
⎟ > 0, to spełniona jest nierówność:
∂
∂
∂
∂
p
V
p
V
S
T
⎛
⎝⎜
⎞
⎠⎟
> ⎛
⎝⎜
⎞
⎠⎟
.
1.46. Pokazać, że dla układu, którego energia wewnętrzna nie zależy od objętości
V, słuszne jest twierdzenie: pojemność cieplna w stałej objętości C
V
zależy tylko od
temperatury.
Rozwiązanie
Korzystając z różniczki zupełnej energii wewnętrznej układu mamy:
( )
dU
U
T
dT g T dT
V
= ⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
.
Podstawiając ten związek do uogólnionej pierwszej zasady termodynamiki, znajdujemy
równanie różniczkowe wiążące entropię i funkcję g(T):
( )
( )
TdS g T dT pdV
T
S
T
g T
V
=
+
⇒
⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
.
Lewa strona tego równania zawiera określenie C
V
, zatem:
( )
C
T
S
T
g T
V
V
= ⎛
⎝⎜
⎞
⎠⎟
=
∂
∂
, cbdw.
1.47. Znaleźć zmianę entropii układu dla przypadku rozszerzalności tego układu
przy stałym ciśnieniu.
Rozwiązanie
Wiemy
już, że entropia jako funkcja stanu układu, może być określona na dwa
sposoby: raz jako funkcja parametrów T i V oraz parametrów T i p:
(
)
( )
⎩
⎨
⎧
=
=
.
p
,
T
S
S
,
V
,
T
S
S
Stąd różniczki zupełne tych funkcji są równe:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
dp
p
S
dT
T
S
dS
,
dV
V
S
dT
T
S
dS
T
p
T
V
Z drugiego równania widać, że dla procesu izobarycznego dp = 0, różniczka entropii
dana jest przez:
( )
dS
S
T
dT
p
p
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Ponieważ dla procesu rozszerzalności termicznej przy stałym ciśnieniu, objętość zależy tylko
od temperatury, to z odwrotnej zależności T = T(V) wynika związek:
dT
T
V
dV
p
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Różniczka zupełna entropii przy stałym ciśnieniu może więc być przekształcona jak
następuje:
( )
dS
S
T
T
V
dV
S
V
dV
p
p
p
p
= ⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
∂
∂
.
Dalej to ostatnie wyrażenie przekształca się przez proste rozszerzenie pochodnej do postaci:
( )
dV
V
T
T
1
T
S
T
dV
V
T
T
S
dV
V
S
dS
p
p
p
p
p
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
.
Wykorzystując dalej definicję pojemności cieplnej ostatni rezultat daje się zmodyfikować
następująco:
dV.
α
1
TV
C
dV
V
T
V
V
1
1
T
C
dV
T
V
1
T
C
(dS)
p
p
p
p
p
p
⋅
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Teraz ewidentnie widać, że zmiana entropii dla przypadku rozszerzalności termicznej
w procesie izobarycznym jest wprost proporcjonalna do względnej zmiany objętości:
.
V
dV
T
C
dS
p
p
⋅
⋅
α
=
1.48. Znaleźć zależność zmiany temperatury w funkcji zmiany ciśnienia dla układu
adiabatycznego (zjawisko termosprężystości).
Rozwiązanie
Dla
układu adiabatycznego, startując ze związku Maxwella, wyrażającego pochodne
cząstkowe potencjałów dla dwóch stopni swobody, przez pochodne odpowiednich zmiennych
niezależnych:
∂
∂
∂
∂
T
p
V
S
S
p
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝⎜
⎞
⎠⎟
,
możemy prawą stronę tego związku wyrazić przez pojemność cieplną układu:
p
p
T
S
T
C
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
i współczynnik rozszerzalności termicznej:
α
∂
∂
=
⋅ ⎛
⎝⎜
⎞
⎠⎟
1
V
V
T
p
,
jak następuje:
.
C
T
V
V
1
TV
p
S
T
T
V
T
V
T
T
S
1
V
S
1
S
V
p
T
p
p
p
p
p
p
p
p
S
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
W nawiasach prostokątnych w ostatnich wyrażeniach stoją przytoczone wyżej definicje. w ten
sposób zależność zmiany temperatury w funkcji zmiany ciśnienia jest opisana równaniem:
.
C
V
T
p
T
p
S
α
⋅
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
1.49. Wykazać, że jeżeli równanie stanu dla układu ma postać p = p(T, V) to
prawdziwy jest związek:
p
=
⋅
κ α
β
, gdzie: κ
∂
∂
= − ⎛
⎝⎜
⎞
⎠⎟
V
p
V
T
oznacza moduł sprężystości
objętościowej w stałej temperaturze, β
∂
∂
= ⎛
⎝⎜
⎞
⎠⎟
⋅
p
T
p
V
1
cieplny współczynnik ciśnienia
przy stałej objętości, α
∂
∂
=
⋅ ⎛
⎝⎜
⎞
⎠⎟
1
V
V
T
p
współczynnik rozszerzalności objętościowej
przy stałym ciśnieniu.
Rozwiązanie
Dane jest równanie stanu p = p(T, V) na mocy, którego różniczka zupełna ciśnienia
przyjmuje postać:
dp
p
T
dT
p
V
dV
V
T
= ⎛
⎝⎜
⎞
⎠⎟
+ ⎛
⎝⎜
⎞
⎠⎟
∂
∂
∂
∂
Prawą stronę tego równania przekształcimy jak następuje
.
dV
V
1
V
p
V
pdT
T
p
p
1
dV
V
V
V
p
dT
p
p
T
p
dp
T
V
T
V
⎟
⎠
⎞
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
Nawiasami prostokątnymi wyróżniono podane wyżej definicje odpowiednich wielkości.
Uwzględniając te definicje, otrzymany rezultat na tym etapie przyjmuje formę:
dp
pdT
V
dV
= ⋅
−
β
κ
.
Dalej dla procesu izobarycznego dp = 0 i ostatnie równanie pozwala wyrazić ciśnienie przez
współczynnik rozszerzalności termicznej według algorytmu:
0
1
= ⋅ −
⎛
⎝⎜
⎞
⎠⎟
⇒
= ⋅ ⎛
⎝⎜
⎞
⎠⎟
= ⋅
β
κ ∂
∂
κ
β
∂
∂
κ
β
α
p
V
V
T
p
V
V
T
p
p
.
W ten sposób kończy się procedura dowodu słuszności związku łączącego ze sobą
zdefiniowane wyżej wielkości współczynników fenomenologicznych charakteryzujących
układ termodynamiczny:
p
= ⋅
κ
β
α
.
1.50. Dla pewnego gazu eksperymentalnie ustalono, że iloczyn ciśnienia i objętości
właściwej, zależy tylko od temperatury. Ustalono również, że energia wewnętrzna
jest również tylko funkcją temperatury. Co można powiedzieć o równaniu stanu
dla tego gazu z punktu widzenia termodynamiki.
Rozwiązanie
Z
treści zadania słuszne są relacje wyjściowe:
( )
( )
pV f T
U U T
=
=
⎧
⎨
⎩
Zapisując równanie na różniczkę zupełną funkcji stanu jaką jest entropia, możemy
wyznaczyć pochodną energii wewnętrznej w stałej temperaturze według standardowego
schematu:
dS
dU pdV
T
dU
dV
T
dS
dV
p
U
V
T
p
T
p
T
V
=
+
⇒
=
−
⇒ ⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
−
∂
∂
∂
∂
.
Pomnożenie tego ostatniego równania stronami przez objętość V, prowadzi do równania:
V
U
V
TV
p
T
pV
T
V
∂
∂
∂
∂
⎛
⎝⎜
⎞
⎠⎟
=
⎛
⎝⎜
⎞
⎠⎟
−
ale ciśnienie na mocy postaci równania stanu danego w treści zadania spełnia następującą
relacje:
∂
∂
∂
∂
p
T
f
T
V
V
df
dT
V
V
⎛
⎝⎜
⎞
⎠⎟
= ⎛
⎝⎜
⎞
⎠⎟
=
1
1
.
Dlatego też poprzednie równanie przyjmuje postać:
V
U
V
T
df
dT
pV
T
∂
∂
⎛
⎝⎜
⎞
⎠⎟
=
−
.
Biorąc pod uwagę fakt, że U = U(T) to
∂
∂
U
V
T
⎛
⎝⎜
⎞
⎠⎟
= 0 i powyższe równanie redukuje się do
równania o rozdzielonych zmiennych::
.
f
dT
df
T
0
−
=
Całkując to równanie otrzymujemy zależność f = f(T):
( )
f T
const T
=
⋅
gdzie const jest stałą całkowania. Podstawiając postać funkcji f do związku na iloczyn p
⋅V
otrzymujemy równanie stanu tego układu:
T
const
pV
⋅
=
.
Widzimy, że jest to równanie stanu gazu doskonałego.
51. Znaleźć entalpię H = H(S, p) układu, dla którego termodynamiczny potencjał jest dany
równaniem:
2
2
1
2
2
1
0
Ep
DTp
CT
Bp
AT
G
G
+
+
+
+
+
=
,
gdzie A, B, C, D, E są stałymi, a G
0
jest potencjałem układu w stanie równowagi.
Ponieważ z definicji potencjał Gibsa spełnia relację:
Vdp
SdT
dG
+
−
=
,
to entropia może być określona przez potencjał Gibsa tego układu za pomocą równania:
S
G
T
p
= ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Z drugiej strony:
G = U - TS + p V = H - TS,
stąd:
H = G + TS
Podstawiając za S do tego równania pochodną przytoczoną wyżej mamy równanie
Helmholtza:
H G T
G
T
p
= − ⎛
⎝⎜
⎞
⎠⎟
∂
∂
.
Z treści zadania:
∂
∂
G
T
A
C T D
p
⎛
⎝⎜
⎞
⎠⎟
= +
⋅
+
1
2
2
p
,
zatem
.
Ep
CT
Bp
G
DpT
CT
AT
Ep
DTp
CT
Bp
AT
G
H
2
2
1
2
2
1
0
2
2
2
1
2
2
1
0
+
−
+
=
−
−
−
+
+
+
+
+
=
Ponieważ:
,
S
-
=
Dp
+
CT
+
A
to
T
S A Dp
C
= −
+ +
.
Mamy zatem wyrażenie na entalpię jako funkcję entropii S i ciśnienia p daną przez równanie:
(
)
H G
Bp
Ep
S A Dp
C
=
+
+
− ⋅
+ +
0
2
2
1
2
1
2
, cbdo.
Literatura
[1]
. K. Stachulec, Wykłady z fizyki klasycznej, Skrypt nr 317, Wydawnictwo PŚk,
Kielce(1997).
[2].
K. Stachulec, Metody rachunkowe fizyki klasycznej w zadaniach z rozwiązaniami, Skrypt
nr 318, Wydawnictwo PŚk, Kielce(1997).
[3].
K. Stachulec, Wprowadzenie do mechaniki kwantowej i fizyki statystycznej, Skrypt nr
323, Wydawnictwo PŚk, Kielce(1998).
[4].
J. Orear, Fizyka, WNT, Warszawa (1993).
[5].
A. K. Wróblewski, J. A. Zakrzewski, Wstęp do fizyki, PWN, Warszawa (1991).
[6].
D. Stauffer, H. E. Stanley, Od Newtona do Mandelbrota, WNT, Warszawa (1996).
[7].
C. Kittel, W. D. Knight, M. A.Ruderman, Mechanika, PWN, Warszawa (1975).
[8].
E.M. Purcel, Elektryczność i magnetyzm, PWN, Warszawa (1975).
[9].
F. S. Crawford, Fale, PWN, Warszawa (1975).
[10].
E. H. Wichmann, Fizyka kwantowa, PWN, Warszawa (1975).
[11].
R. Reif, Fizyka statystyczna, PWN, Warszawa (1975).
[12].
M. Toda, R. Kubo, N. Saitô, Fizyka statystyczna, PWN, Warszawa (1991).
[13].
G. L. Squires, Praktyczna fizyka, PWN, Warszawa (1992).
[14].
W. K. Kobuszkin, Metodyka rozwiązywania zadań z fizyki, PWN, Warszawa (1987).
Document Outline