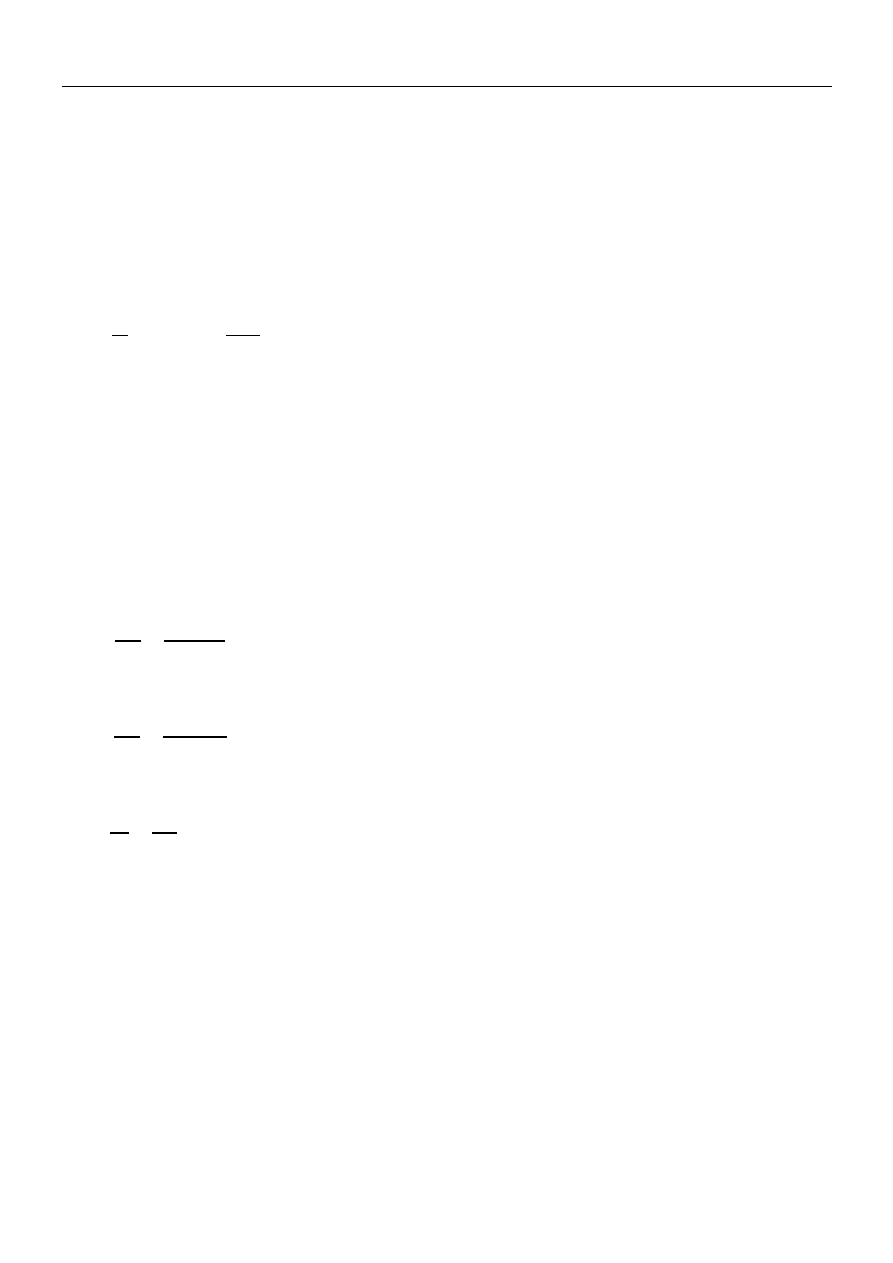
str. 1

/13

1. Dane statku i obliczenia początkowe.

długość między pionami

L

=

154

[ m ]

szerokość

B

=

22,44

[ m ]

zanurzenie konstrukcyjne

T

=

7,04

[ m ]

wysokość

H

=

10,56

[ m ]

objętość podwodnej części kadłuba

V

=

14621,89

[ m

3

]

odcięta środka wyporu

X

B

=

-4,35

[ m ]

podajemy w formie procentowej

(wg przepisów PRS)

odcięta środka wyporu

X

B

=

-2,82

[ % ]

rzędna środka wyporu

Z

B

=

3,86

[ m ]

współczynnik pełnotliwości kadłuba

C

B

=

0,60

[ - ]

odległość miedzy wodnicami

z

=

0,88

[ m ]

skala geometryczna

=

101,99

[ - ]

odstęp międzywręgowy

d

=

15,4

[ m ]

pole przekroju wodnicy konstrukcyjnej

A

W

=

2717,13

[ m

2

]

pole przekroju owręża do wodnicy

A

M

=

143,91

[ m

2

]

współczynnik pełnotliwości wodnicy

C

W

=

0,79

[ - ]

współczynnik pełnotliwości owręża

C

M

=

0,91

[ - ]

współczynnik pełnotliwości wzdłużnej

C

P

=

0,66

[ - ]

pole zwilżonej części pawęży

A

T

=

0,9179

[ m

2

]

pole przekroju wrężnicowego

A

BT

=

90,98

[ m

2

]

str. 2

/13

str. 3

/13

2. Założenia projektowe.



prędkość

v

=

17

[ kn ]



prędkość

v

=

8,7

[ m/s ]



gęstość wody

=

1,025 [ t/m

3

]



przyspieszenie ziemskie

g

=

9,81 [ m/s

2

]



ilość obrotów śruby

n

=

120 [ obr/s ]



liczba łopatek na śrubie

z

=

5

[ - ]



współczynnik wyprostowania powierzchni kawitacji



jednośrubowiec



kształt części rufowej jest normalny

str. 4

/13

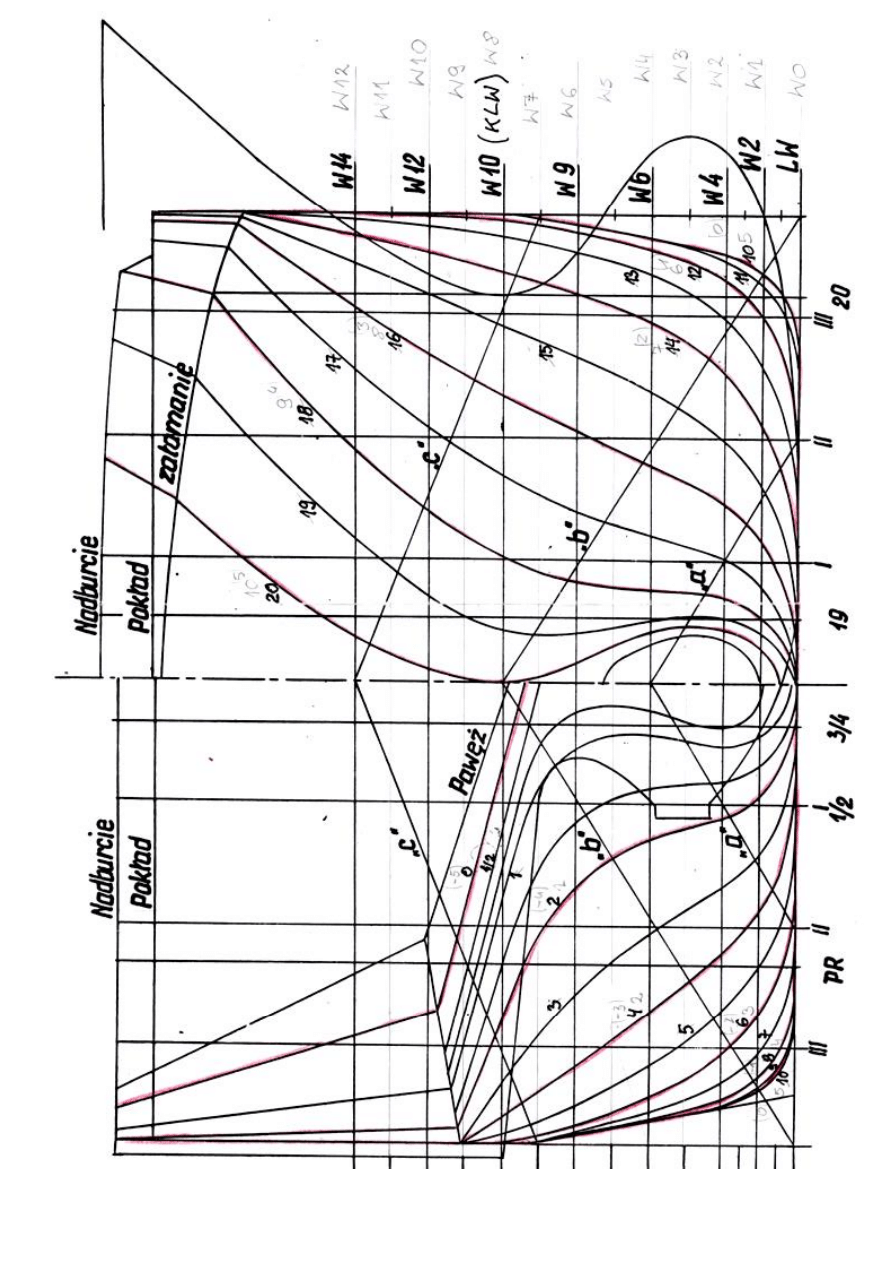
3. Obliczanie maksymalnego promienia śruby.

Obliczenie R

max

z przepisów PRS część II Kadłub.

Rysunek parametrów odległościowych umiejscowienia śruby potrzebnych do obliczenia promienia

maksymalnego dla jednośrubowca:

a 2 R

b ( z) R

c ( 2 z) R

e R

e 2R c hs

Po podstawieniu danych i wyliczeniu:
R

max

= 2,71 m.

D

max

= 5,41 m.

str. 5

/13

4. Obliczenia części wystających: steru i stępki.

STER

Pole powierzchni (wg przepisów DNV).

[ m

2

]

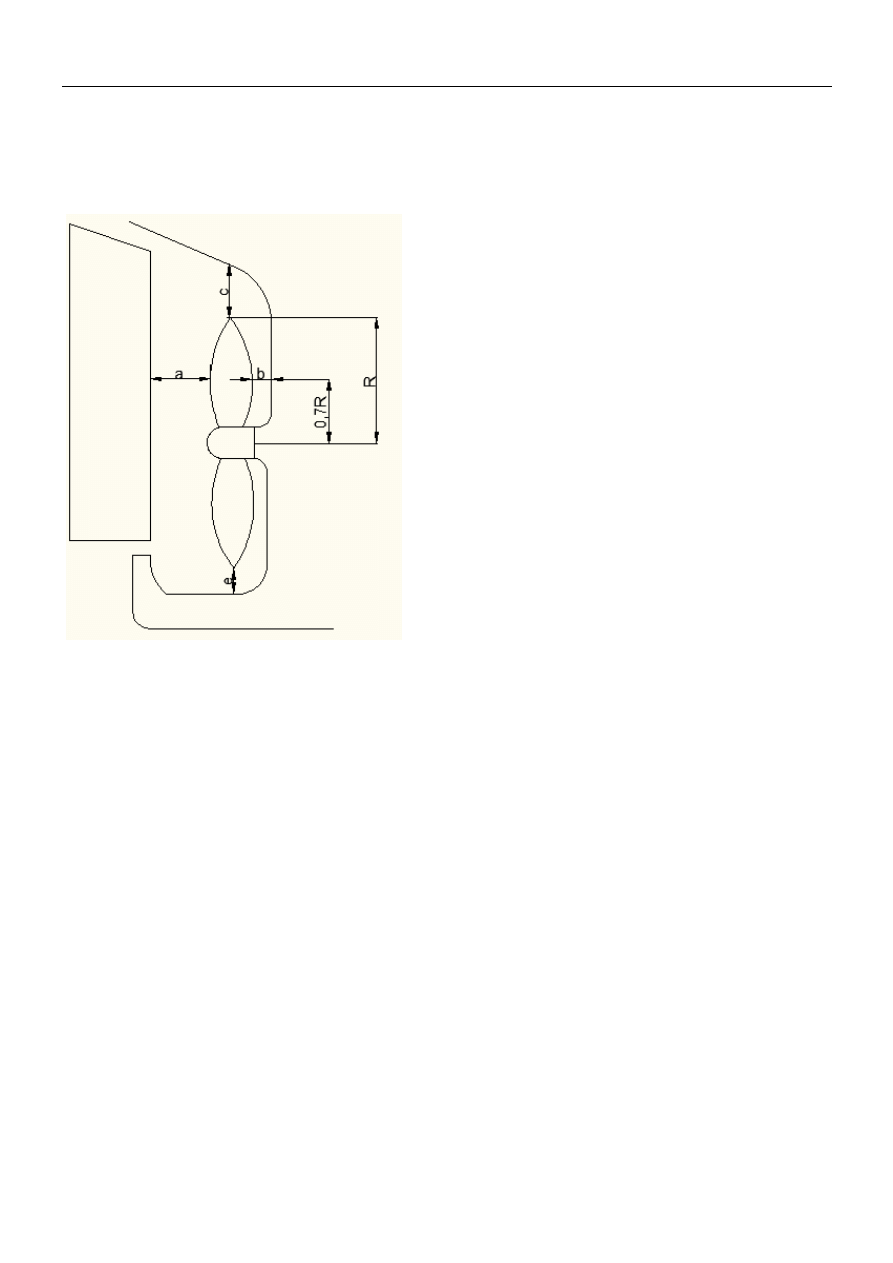
STĘPK

Rysunek stępki obłowej:

Wymiary stępki obłowej:

51,3 [ m ]

2 22 [ m ]

2 [ m

2

]

Zakładamy taką samą odległość stępek po obu stronach.

CAŁKOWITE PO E ZĘŚ I Z NURZONY H

S

APP

= A

R

+ A

S

= 14,99 + 92,15 = 107,14 [ m

2

]

PO E ZWI ŻONEJ ZĘŚ I K DŁU

S (2 T )

2

2 2

2

(2 22 ) 2 2 2

22,447,04 2 90,980,6=4318,78 [ m

2

]

Kąt wejścia do wody: α 0

o

str. 6

/13

5. Wyznaczanie oporu okrętu oraz krzywej oporu.

Wykorzystamy metodę Holtropa-Mennena którą opisuje się na podstawie pomiarów oporów

modeli oraz okrętów rzeczywistych. Wzory wykorzystywane w tej metodzie polegają na

uzależnieniu składników oporu całkowitego okrętu od prędkości wymiarów głównych i

parametrów kształtu kadłuba.

Wzór na opór całkowity kadłuba:

R

R

( k

) R

R

R

R

R

2 2 2 2 2

2 N 2 [ kN ]

R

F0

– opór tarcia ekwiwalentnej płaskiej płyty

(1+k

1

) – współczynnik kształtu

R

APP

– opór części wystających

R

W

– opór falowy

R

B

– dodatkowy opór ciśnienia wywołany gruszką dziobową

R

TR

– dodatkowy opór ciśnienia wywołany zanurzoną pawężą

R

A

– poprawka uwzględniająca korelację modelu okrętu

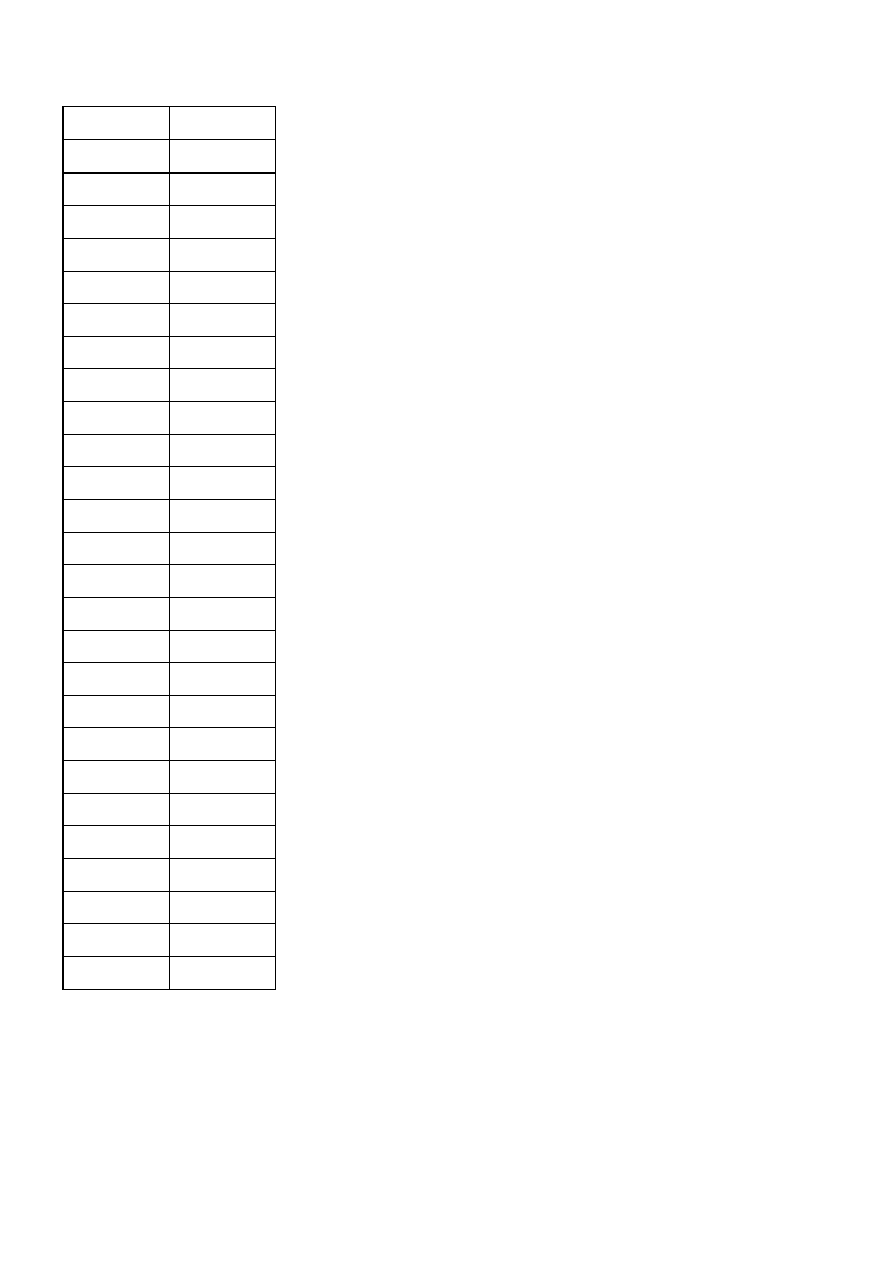
str. 7

/13

Tabela przedstawia całkowity opór kadłuba dla poszczególnych prędkości wyrażonych w węzłach.

v

R

T

[ kn ]

[ kN ]

1

0,9147

2

3,4867

3

7,6367

4

13,3268

5

20,3710

6

29,2350

7

39,4228

8

52,0931

9

64,2664

10

79,0042

11

95,4326

12

113,7412

13

134,1192

14

157,3678

15

182,4220

16

212,8562

17

246,4191

18

278,5225

19

318,5439

20

374,3396

21

441,3520

22

502,8134

23

550,4466

24

592,0206

25

638,7058

Do dalszych obliczeń przyjmuje prędkość kn ponieważ jest to taka największa prędkość gdzie

współczynnik wyprostowanej powierzchni kawitacji będzie mniejszy od - czyli nie będzie

występowała kawitacja.

str. 8

/13

0

50

100

150

200

250

300

350

400

450

500

550

600

650

700

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

R

T

[

k

N

]

v [ kn ]

Zależność oporu od prędkości

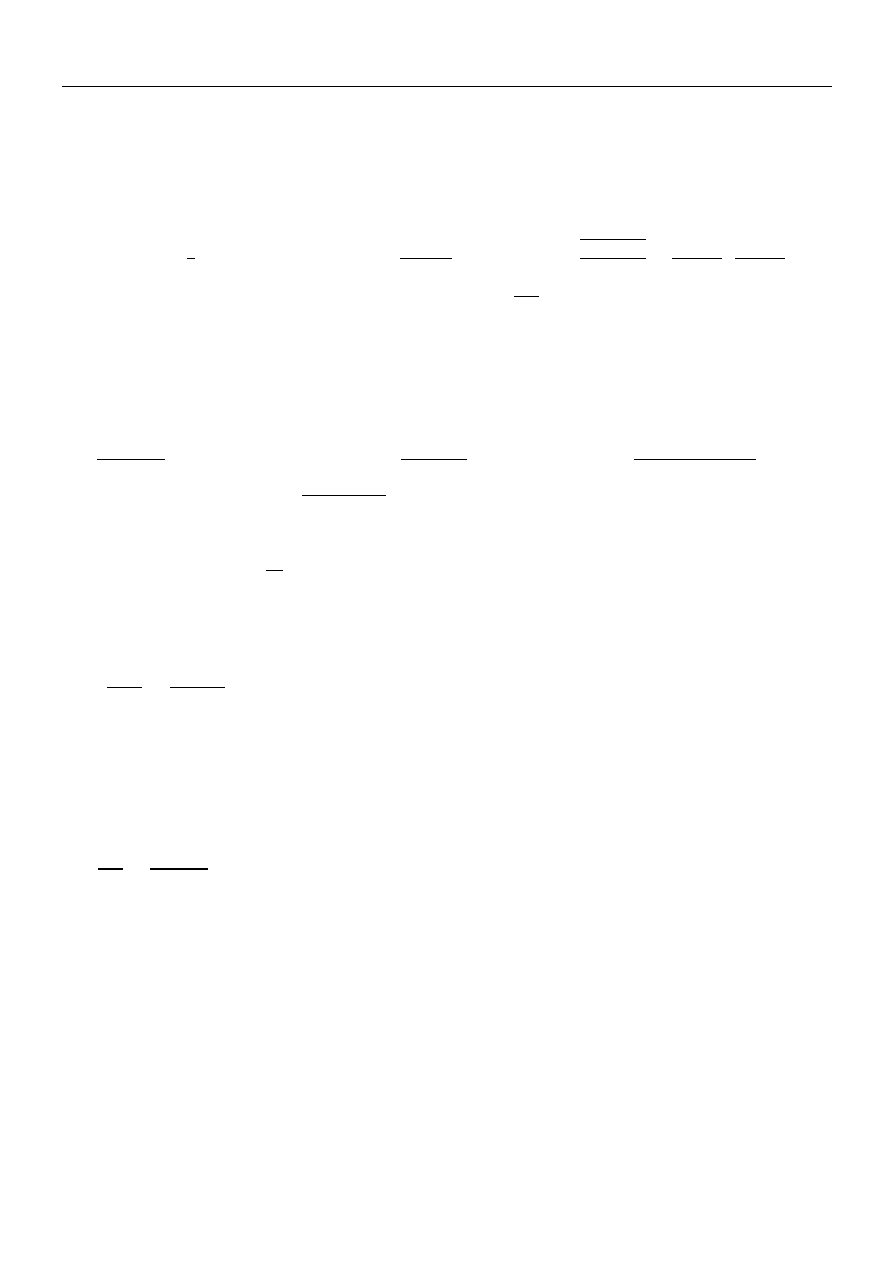
str. 9

/13

6. Określenie współczynników wzajemnego oddziaływania kadłuba i śruby.

Do znalezienia współczynników użyjemy wzorów Holtropa-Mennena. Dzięki zastosowaniu tych

wzorów jesteśmy w stanie policzyć współczynnik strumienia nadążającego ssania oraz sprawność

kadłuba i rotacyjną.

WSPÓŁ ZYNNIK STRUMIENI N DĄŻ JĄ EGO

w

2

(

)

2

(

)

2

2

0,0013 2 2 22,44 2 0,09726 0,11434 +

2 22 [ - ]

N STĘPNY TO WSPÓŁ ZYNNIK SS NI

t

2

2

[ - ]

SPR WNOŚĆ ROT YJN

22

2 (

22

) 22 2

2 ( 22 ( 2 2)) [ - ]

SPR WNOŚĆ K DŁU

[ - ]

PRĘDKOŚĆ DOPŁYWU WODY DO PĘDNIKÓW

V

( w

) ( 22 ) [ m/s ]

N PÓR ŚRU Y D PRĘDKOŚ I KN

T

2 [ kN ]

MOC NAPORU

P

T V

2 2 kW ]

str. 10

/13

7. Kryterium kawitacyjne.

Minimalny współczynnik powierzchni wyprostowanej zapewniający bezkawitacyjną pracę śruby

określa wzór Kellera. Nasza śruba wywodzi się z serii -Wargeningen. Jest to jedna z

popularniejszych serii śrub. Jej dane techniczne oscylują w granicach:

2

( )

(

)

K[ - ]

P

o

– ciśnienie w osi śruby

P

a

– ciśnienie na wysokości lustra wody która wynosi 2 hPa

P

v

– ciśnienie pary nasyconej dla temperatury

o

C wynosi 1,707 hPa

D – średnica śruby

K – stała dla okrętów jednośrubowych K 2

Kawitacja jest to proces powstawania obszarów nieciągłości w płynie na skutek spadku ciśnienia w

owych obszarach ponieważ spada tam ciśnienie poniżej pewnej krytycznej wartości. Wtedy w tych

miejscach zostają wypełnione mieszaniną cieczy i gazów na wskutek czego powstaje implozja.

Zjawisko implozja negatywnie wpływa na śruby okrętowe wywołując zniszczenia. zyli
podsumowując nie chcemy aby to zjawisko miało miejsce.

str. 11

/13

8. harakterystyki hydrodynamiczne i dobór śruby.

W tym punkcie zajmiemy się zależnościami współczynnika naporu i momentu od współczynnika

posuwu współczynnika skoku współczynnika powierzchni wyprostowanej oraz liczby skrzydeł.

Wszystkie te zależności można przedstawić za pomocą zależności które są podane poniżej:

 

v

u

v

u

t

s

o

E

t

s

v

u

t

s

RT

T

z

A

A

D

P

J

C

K





























)

,

,

,

(

,

,

,

)

(

 

v

u

v

u

t

s

o

E

t

s

v

u

t

s

KQ

Q

z

A

A

D

P

J

C

K





























)

,

,

,

(

,

,

,

)

(

harakterystyki przedstawiają się następująco:



współczynnik naporu
K



współczynnik momentu
K



współczynnik posuwu
J



współczynnik skoku



sprawność pędnika

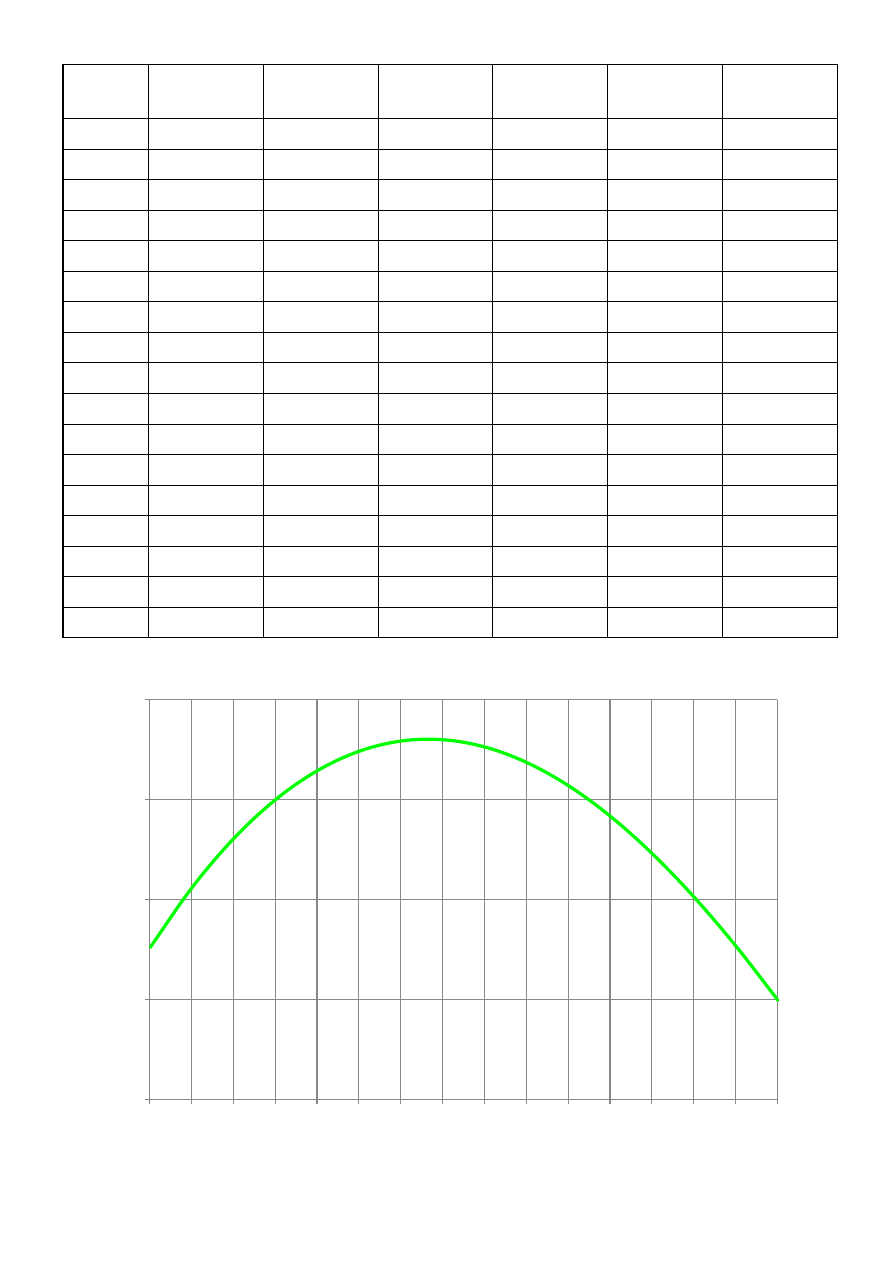
str. 12

/13

średnica

współczynnik

naporu

współczynnik

posuwu

kryterium

kawitacyjne

współczynnik

skoku

współczynnik

momentu

sprawność

pędnika

D

KT

J

A

E

/A

O

P/D

KQ

p

5,41

0,08441

0,62706

0,63023

0,73059

0,01404

0,59982

5,31

0,09095

0,63887

0,64658

0,75503

0,01508

0,61331

5,21

0,09814

0,65113

0,66389

0,78102

0,01626

0,62558

5,11

0,10604

0,66386

0,68221

0,80873

0,01760

0,63647

5,01

0,11476

0,67711

0,70165

0,83833

0,01915

0,64582

4,91

0,12440

0,69090

0,72228

0,87005

0,02093

0,65348

4,81

0,13507

0,70525

0,74422

0,90414

0,02299

0,65931

4,71

0,14690

0,72022

0,76756

0,94088

0,02539

0,66319

4,61

0,16007

0,73584

0,79244

0,98063

0,02819

0,66503

4,51

0,17474

0,75215

0,81900

1,02378

0,03147

0,66471

4,41

0,19113

0,76920

0,84738

1,07081

0,03534

0,66217

4,31

0,20948

0,78704

0,87776

1,12227

0,03992

0,65732

4,21

0,23010

0,80572

0,91032

1,17879

0,04539

0,65007

4,11

0,25331

0,82532

0,94529

1,24106

0,05196

0,64034

4,01

0,27953

0,84589

0,98291

1,30974

0,05992

0,62803

3,91

0,30923

0,86752

1,02345

1,38529

0,06964

0,61306

0,575

0,600

0,625

0,650

0,675

3,91 4,01 4,11 4,21 4,31 4,41 4,51 4,61 4,71 4,81 4,91 5,01 5,11 5,21 5,31 5,41

ηp

[

-

]

D [ m ]

Wykres sprawnosci n = 120 [ obr/min ]

str. 13

/13

9. Podsumowanie

Maksymalna średnica śruby - 5,41 [ m ]

Optymalna średnica śruby- 4,61 [ m ]

n

= 120 [ obr/m ]

v

= 17 [ kN ]

K

T

= 0,16007 [-]

J

= 0,73584[-]

A

E

/A

o

= 0,79244[-]

P/D = 0,98063[-]

K

Q

= 0,02819[-]

P

= 0,66503[-]