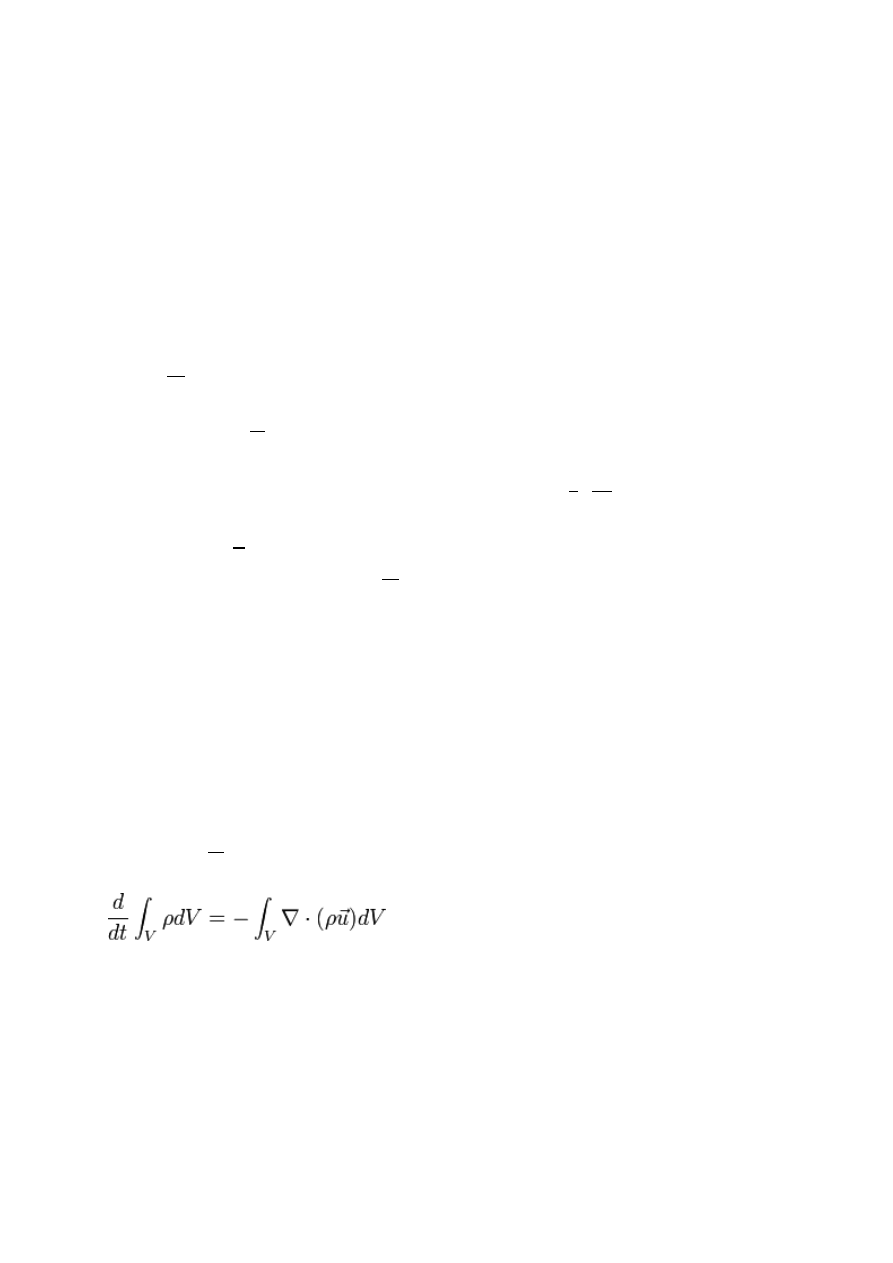
1.Różnice między cieczą a gazem: -cząstki w ciale stałym znajdują sie bliżej niż w cieczach-łatwo
zmienid kształt cieczy, a ciała stałego trudno.-Z wyjątkiem rtęci żadna z cieczy nie jest metalem,
natomiast wiele ciał stałych jest metalami.-ciecze są łatwo rozpuszczalne, a ciała stałe nie. .2.
Ośrodek ciągły – model ciała, w którym zaniedbano cząsteczkową (atomową) budowę
materiiElement płynu – niewielka częśd płynu. Jest to objętośd płynu na tyle mała, by można było
przyjąd iż wszystkie własności płynu są w niej jednakowe, a jednocześnie na tyle duża, by można było
stosowad metody statystyczne (wobec chaotycznego ruchu molekuł) do ich wyznaczania. Pojęcie
używane w mechanice płynu w tworzonych modelach zachowania się płynu.3. Siły działające w
płynach:-masowe: ciężkości, bezwładności ( d’Alamberta)- działają wówczas gdy płyn znajduje się w
polu sił (ciężkości, bezwładności). Cechą charakterystyczną tych sił jest to, że działają one na
wszystkie cząstki rozpatrywanej objętości płynu.Jednostkową siłę masową definiujemy w postaci:q=

= ix+ jY+ kZgdzie,q=(X,Y,Z) - jest wektorem głównych sił masowych- powierzchniowe:

zewnętrzne (np. nacisk tłoka), wewnętrzne (naprężenia,napięcia)Siły powierzchniowe σ definiujemy

w postaci:σ=

w ogólnym przypadku: σ=σ(x, y, z, t,

,

,

)4. Własności płynów:

Masa

jest właściwością płynu charakteryzującą jego ilość.Gęstość ρ lub odwrotność objętości

właściwej υ; w dowolnym punkcie płynu określa zależnośćρ=

=

będąca stosunkiem

elementarnej masy płynu dm do objętości dV w której jest ona zawarta.Dla płynu
nieściśliwego:ρ=

Jednostką gęstości w układzie SI jest l kg/m

3

.Gęstość gazu wyznaczamy z

równania stanu gazu (Clapeyrona):ρ=

gdzie:p - ciśnienie,T - temperatura (w skali

bezwzględnej Kelwina),R - indywidualna stała gazowa;Podstawową jednostką ciśnienia w
układzie SI jest l N/m

2

= 1 Pa.5. Pole fizyczne:

ciągłe układy fizyczne o nieskończonej

liczbie stopni swobody - np. pole grawitacyjne, pole elektromagnetyczne itp. Opis pola polega
na określeniu w każdym punkcie i dla każdej chwili czasu wielkości fizycznych
charakteryzujących to pole, dokonuje się tego podając odpowiednie funkcje ciągłe opisujące
pole.6. zasada zachowania masy: Zgodnie z zasadą zachowania masy, w żadnym punkcie
pola masa nie może się tworzyć ani znikać. W płynie nieściśliwym (ρ = const) tylko takie
pole prędkości będzie spełniało tę zasadę, w którym w każdej chwili do obszaru
ograniczonego powierzchnią kontrolną będzie wpływało tyle płynu, ile w tej samej chwili
wypływa.W dynamice płynów lokalną zasadę zachowania masy wyraża wzór w postaci
różniczkowej:

+

* (ρu)= 0gdzie:ρ – gęstość płynu,u – prędkość płynu,t – czas.Równanie

ciągłości może być również zapisane w postaci całkowej

7. Równanie mechaniki płynów wyrażające zasadę

zachowania masy.

ρ/ + div (ρ*v)=0

10. Postad równania ciągłości przepływu płynu

nieściśliwego oraz ściśliwego w ruchu ustalonym jednowymiarowy-ściśliwy ρ v A = const-
nieściśliwy v A = const.12. Warunki stosowalności równania Eulera. Postad wektorowa i
skalarowa równania EuleraWektorowa: f- 1/ρ grad p= dv/dt / + (v Skalarowa: X-1/ρ*
/ = + Vx* + Vy* + Vz*

Y-1/ρ* / = + Vx* + Vy* + Vz*

Z-1/ρ* / = + Vx* + Vy* + Vz* 13. Potencjał
jednostkowych sił masowychU(x,y,z)= const.X=

/ ,

Y=

/ ,

Z=

/

16. Parcie

wypadkowe i moment układu pard elementarnych?dP=γ*zdF17. Wypadkowa parcia na ścianę
płaską i zakrzywioną – sposób obliczeń - na ścianę płaską

- na ścianę zakrzywioną

,

19. Warunki stateczności ciał

całkowicie zanurzonych w cieczyWarunki stateczności:-Środek ciężkości znajduje się poniżej środka
wyporu - ciało pływa statecznie. -Środek ciężkości ciała jest powyżej środka wyporu – ciało pływa nie
statecznie.-Punkty S i Σ pokrywają się – równowaga obojętna (ciało może pływad w dowolnym
położeniu). -Ciało pływa zawsze statecznie, gdy jego środek ciężkości jest położny poniżej środka
pływania-Gdy środek pływanie jest położony powyżej środka ciężkości, to ciało pływa statecznie lub
niestatecznie. O stateczności pływania decyduje odległośd meta centryczna20. Metacentrum –
sposób obliczeoM – metacentrum, punkt przecięcia linii wyporu przed wychyleniem ciała z punktem
przecięcia linii wyporu po wychyleniu ciała, m– odległośd metacentryczna, odległośd pomiędzy
punktami M i Sc.m > 0 gdy punkt M leży powyżej punktu Scm < 0 gdy punkt M leży poniżej punktu
ScOdległośd metacentryczną m obliczamy z następującej zależnościGdzie:J – moment bezwładności
przekroju pływania względem osi obrotu,Vzan – objętośd zanurzonej części ciała, a – odległośd
pomiędzy środkiem ciężkości i środkiem pola w stanie nie wychylonym.Ciało pływające na
powierzchni cieczy jest zawsze stateczne, gdy S

c

leży poniżej S

p

, gdyż wtedy we wzorze (7) jest

(+a), więc cała wartośd wyrażenia (7) jest zawsze dodatnia. Gdy S

c

leży powyżej S

p

, to ciało może

byd stateczne lub niestateczne. Suma ujemna wartości a jeszcze nie przesądza o stateczności.
Dopiero ujemna lub dodatnia wartośd całego wyrażenia (7) decyduje o nie stateczności m<0, lub
stateczności m>0. 21. przyśpieszenie substancjalne, lokalne, konwekcyjne płynuPojęcie pochodnej

substancjalnej odniesione do dowolnej funkcji H:

Znikanie pochodnej lokalnej

świadczy o stacjonarności pola H, zerowa zaś wartośćpochodnej konwekcyjnej o jego
jednorodności.Jeżeli H jest skalarem, to pochodna substancjalna

22. Równanie

Eulera w postaci Lamba-GromekiKorzystając z tożsamości wektorowej (a

) a = grad (

/2) + rot a

× a, równanieEulera (5.2) możemy przekształcić do postac

grad

p23. Założenia pozwalające uzyskać całki Bernoulliego i Cauchy-Lagrange’a- gdy przepływ jest

potencjalny- całka Cauchy-Lagrange’aJeżeli W = 0, to ruch płynu jest potencjalny i pole prędkości

jest określone zależnościąv = grad

Φ:

- gdy przepływ jest wirowy,

ale ustalony- całka Bernoulliego

Jeżeli ruch płynu jest ustalony, czyli ∂ v/∂ t = 0 to równanie

Eulera w formie Lamba i Gromeki przyjmuje postać:

24.

Interpretacja graficzna równania Bernoulliego

Na rysunku przedstawiono wykres obrazujący zmianę każdej

wysokości w strudze o zmiennym przekroju. Wykres ten składa się z trzech linii:

a

V

J

m

zan





*oś strugi leżąca na wysokości z ponad poziomem odniesienia,*linia ciśnień leżąca o p/



g ponad osią

strugi,*linia energii leżąca o v

2

/2g ponad linią ciśnień

25. Zjawisko kontrakcji. Współczynnik kontrakcji, straty prędkości i wypływu
Zjawisko kontrakcji polega na tym, że zmieszanie dwóch objętości cieczy nie daje w wyniku sumy
tych objętości lecz wartość nieco mniejszą
Stosunek pola przekroju strugi w miejscu przewężenia do pola otworu nazywamy współczynnikiem

kontrakcji (zwężenia)

Wartość tego współczynnika zależy przede wszystkim od liczby

Reynoldsa, a takżeod kształtu i usytuowania otworu wypływowego.26. Zastosowania równania
BernoulliegoRównaniem Bernoulliego opisuje wiele na co dzień obserwowanych zjawisk, zależności,
a także zasad działania licznych urządzeń technicznych:
paradoks hydrodynamicznyzjawisko zrywania dachów, gdy wieje silny wiatrzasada działania rurki
Pitotazasada działania rurki Prandtlazasada działania zwężki Venturiego
zasada działania palnika Bunsenapośrednio zasady powstawania siły nośnej w skrzydle
samolotupośrednio w powstawaniu efektu Magnusaprzyczyna osiadania statków w ruchu na płytkim
akwenie27. Przepływ osiowosymetryczny. W jakim układzie wspórzędnych można go łatwo
opisać?współrzędne prostokątne zastępujemy cylindrycznymi. Ze względu na osiową symetrię ruchu
(prędkość zależy tylko od współrzędnej r)

29. Równanie linii prądu i toru

elementu płynuTor (trajektoria) elementu płynu jest to miejsce geometryczne kolejnych położeń
poruszającegosię elementu płynu z upływem czasu.Równanie różniczkowe toru elementu płynu:

Równanie różniczkowe linii prądu:

31. Strumień objętości, masy

Strumień objętości (objętościowe natężenie przepływu) - iloczyn prędkości przepływu czynnika
(płynu) przepływającego przez przewód rurowy (rurę) i powierzchni przekroju tego przewodu.
Q = vS Q − strumień objętościv − średnia prędkość liniowa czynnika w kierunku przepływu
S − pole powierzchni przekroju rury (dla rury okrągłej o promieniu r: S = π r2)
Strumień objętości nazywany jest również prędkością wolumetryczną lub przepływem
wolumetrycznym (ang. volumetric flow rate).Strumień masy:Qm=ρvs32. Cyrkulacja prędkości-
cyrkulacją prędkości nazywamy całkę liniową po konturze zamkniętym S z iloczynu prędkości
stycznej do konturu vs i elementu drogi ds.:Γ=∫ vs ds.=∫(vx dx+ vy dy+ vz dz) – cyrkulacja prędkości
w ruchu potencjalnym= 0, istnieje tylko w ruchu wirowym33. Strumień wirowości płynuqW = divW
dV34. Treść twierdzenia Stokesacyrkulacja pola wektorowego po zamkniętym i zorientowanym
konturze gładkim jest równa strumieniowi rotacji pola przez dowolną powierzchnię ograniczoną tym
konturem35. Treść pierwszego twierdzenia Helmholtza

wzdłuż rurki wirowej strumień wirowości

obliczany dla dowolnego przekroju tej rurki jest wielkością stałą.36. Postać wektorowa równania
Naviera-Stokesa dla przepływu płynu ściśliwego i nieściśliweg-ściśliwy f- 1/ρ grad p + μ/ρ

v +

μ/ρ grad div v= dv/dt-nieściśliwy f- 1/ρ grad p + μ/ρ

v = dv/dt

37. Równanie Naviera-Stokesa dla przepływu cieczy w układzie współrzędnych prostokątnych
X-1/ρ*

p/ x + μ/ρ*

Vx+

μ/ρ

/ x div v= dVx/dt/Y-1/ρ* p/ y + μ/ρ

Vy+

μ/ρ*

/ y

div v= dVy/dt/Z-1/ρ*

p/ z + μ/ρ

Vz+

μ/ρ

/ z div v= dVz/dt40. Wektorowe równanie

Naviera Stokesa w najbardziej ogólnej postaci - uproszczeia aż do uzyskania równania
opisującego prawo Paskala

grad( )

dV

F

p

V

dt











 

41. Postać równania

energiicałkowitejwynikające z zasady zachowania energii. Przyczyny wywołujące zmiany energii
całkowitej płynuρ* d/dt*(

/2+e)= div (S*v)+ρ f v+ div (λ grad T)

42. Postać równania energii kinetycznej płynu - sposób jej uzyskania. Siły decydujące o zmianie
energii kinetycznejEnergia kinetyczna płynu Ekśr obliczona dla prędkości średniej jest jednak na
ogółróżna od energii kinetycznej rzeczywistej Erz, będącej całką energii kinetycznej strug
elementarnych. Energia kinetyczna masy qm Δt poruszającej się z prędkością vśr
Eśr= q* m* ∆ t*

/2= ρ*A*

/2* ∆ t45.Równanie Bernoulliego dla przepływów

rzeczywistych

/2g + p1/ρg + z1=

/2g + p2/ρg + z246. Straty energii wywołane tarciem

∆

= λ* 1/d *

/2gznanej pod nazwą wzoru Darcy’ego–Weisbacha,

w której:l – długość przewodu,d – średnica przewodu,v – średnia prędkość przepływu,λ –
współczynnik oporu liniowego (strat tarcia).47. Straty energii wywołane oporami miejscowymi

=

=

(Re)*

/2g