1.
Siły masowe i powierzchniowe w przepływie
Siły powierzchniowe (kontaktowe) – to takie których oddziaływanie na ośrodek jest przenoszone poprzez powierzchnię kontaktu, są to siły o małym zasięgu
(3 składowe) x (3 orientacje) = 9
zz
zy
zx
yz
yy
yx
xz
xy
xx
Siły masowe - to takie które przenoszą się na każdy punkt materialny ośrodka, działają na duże odległości
k
F
j
F
i
F
F
z
y
x
N
k
f
j
f
i
f
f
z
y
x
2
/ m
N
2.
Warunek równowagi de Alemberta
Siły masowe
f
0
dV
dV
dm
dV
f
dm
f
F
d
V
dV
f
F
Siły powierzchniowe
2
/ m
N
p
dA
n
n
n
p
dA
n
p
A
d
P
d
z
y
x
1
0
0
0
1
0
0
0
1
pdA
dA
n
p
dA
n
n
n
p
P
d
z
y
x
A
pdA
P
W przypadku równowagi
0
P
F
Z tw. Gaussa Ostrogradskiego
0
A
V
pdA
dV
f
V
A
dV
v
pdA
Zatem
0
V
V
pdA
v
dV
f
0
V
dV
p
v
f
Dla
0
dV
v
mamy
0
p
v
f
czyli
f
p
v
1
Dopisując składowe
x
f
y
f
z
f
i mnożąc odpowiednio przez
dx dy dz
mamy
dx
f
dx
x
p
x
1
dy
f
dy
y
p
y
1
dz
f
dz
z
p
z
1
dz
f
dy
f
dx
f
dz
z
p
dy
y
p
dx
x
p
z
y
x
1
dz
f
dy
f
dx
f
dp
z
y
x
1
Biorąc pod uwagę że
p
grad
p
v
v
f
1
Na powierzchni stałego potencjału
const
v
0
dz
f
dy
f
dx
f
z
y
x
3.
Napór hydrostatyczny
Wypadkowa siła to ciecz będąca w stanie równowagi, działająca na ścianę lub jej fragment.
Siła naporu od strony wewnętrznej
A
A
w
A
d
gz
p
A
pd
P
0
Siła naporu od strony zewnętrznej
A
z
A
d
p
P
0
Napór hydrostatyczny
A
A
z
w
A
d
p
A
d
gz
p
P
P
P
0
0
dA
n
A
d
k
k
n
j
j
n
i
i
n
k
n
j
n
i
n
n
n
n
z
y
x
,
cos
,
cos
,
cos
k
dA
k
n
j
dA
j
n
i
dA
i
n
dA
n
gz
P
A
A
A
A
,
cos
,
cos
,
cos
Pz
Py
Px
k
gzdA
j
gzdA
i
gzdA
P
Az
Ay
Ax
rzutu
s
x
Ax
Ax
A
z
g
gM
zdA
g
gzdA
Px
rzutu
s
y
Ay
Ay
A
z
g
gM
zdA
g
gzdA
Py
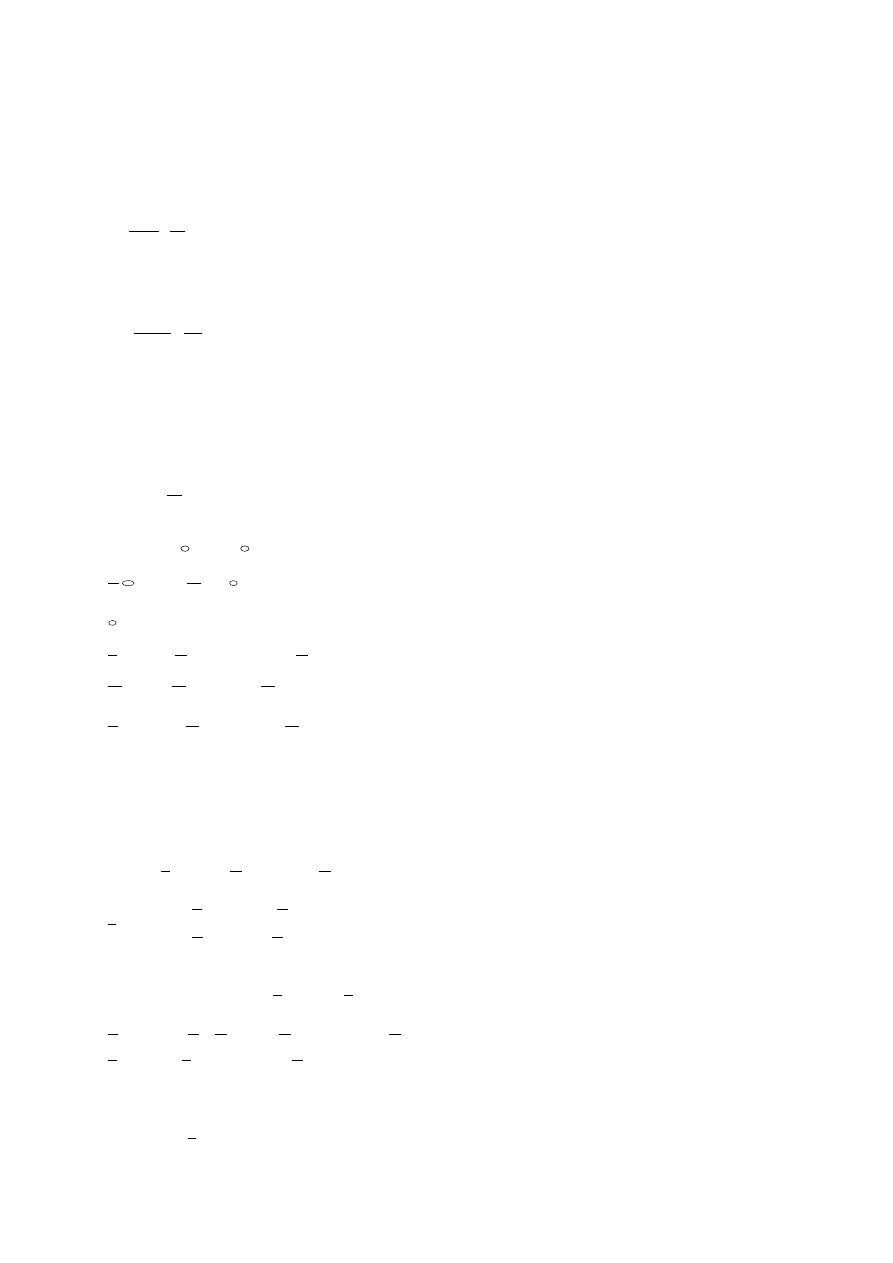
z
Az
Az
gV
zdA
g
gzdA
Pz
Współrzędne środka naporu
Ax
N
x
dA
gz
z
P
Ax
N
x
dA
z
g
z
gM
2
x
x
x
Ax
N
M
I
M
dA
z
z
2
Ax
N
x
dA
gz
y
P
Ax
N
x
yzdA
g
y
gM
x
x
x
Ax
N
M
D
M
yzdA
y
4.
Twierdzenie Reynoldsa o transporcie
Pole wielkości ekstensywnej
t
r
R ,
0
dV
3
R
V
dV
Sumarycznie
V
RdV
Zmiana może być wywołana na 2 sposoby
Zmiana lokalna pola R
0
dV
V
dV
t
V
Wymiana z otoczeniem przez powierzchnię brzegową A na drodze konwekcji (unoszenia) z prędkością
v
A
A
A
d
v
R
dA
n
v
R
dA
n
v
R
A
V
V
A
d
v
R
dV
t
R
RdV
dt
d
Z twierdzenia Gaussa-Ostrogradskiego
V
A
dV
v
R
A
d
v
R
V
V
V
V
dV
v
R
t
R
dV
v
R
dV
t
R
RdV
dt
d
v
R
dt
dR
v
R
R
v
t
R
v
R
t
R
Twierdzenie Reynoldsa
V
V
V
dV
v
R
dt
dR
dV
v
R
t
R
RdV
dt
d
5.
Ogólne sformułowanie zasad zachowania (masy, pędu)
0
dV
dV
dm
sumaryczna masa
V
dV
Zmiana masy
V
V
V
dV
v
dt
d
dV
v
t
dV
dt
d
Dla układu izolowanego, gdy masa jest zachowana
0
0
0
0
0
v
dt
d
dV
v
dt
d
v
t
dV
v
t
dV
dt
d
V
V
V
Zachowanie pędu
0
dV
dV
dm
dV
v
dm
v
sumaryczny pęd
V
dV
v
Zmiana pędu
V
V
dV
v
v
v
dt
d
dV
v
dt
d
Zauważmy
dt
v
d
v
v
v
v
dt
v
d
v
v
dt
d
v
dt
dv
v
v
v
dt
d
V
V
V
dV
dt
v
d
dV
v
v
v
dt
d
dV
v
dt
d
Dla układów nie izolowanych mamy
Siły masowe
f
,
0
dV
dV
dm
V
dV
f
F
dV
f
dm
f
F
d
Siły powierzchniowe
,
dA
n
A
d
0
dA
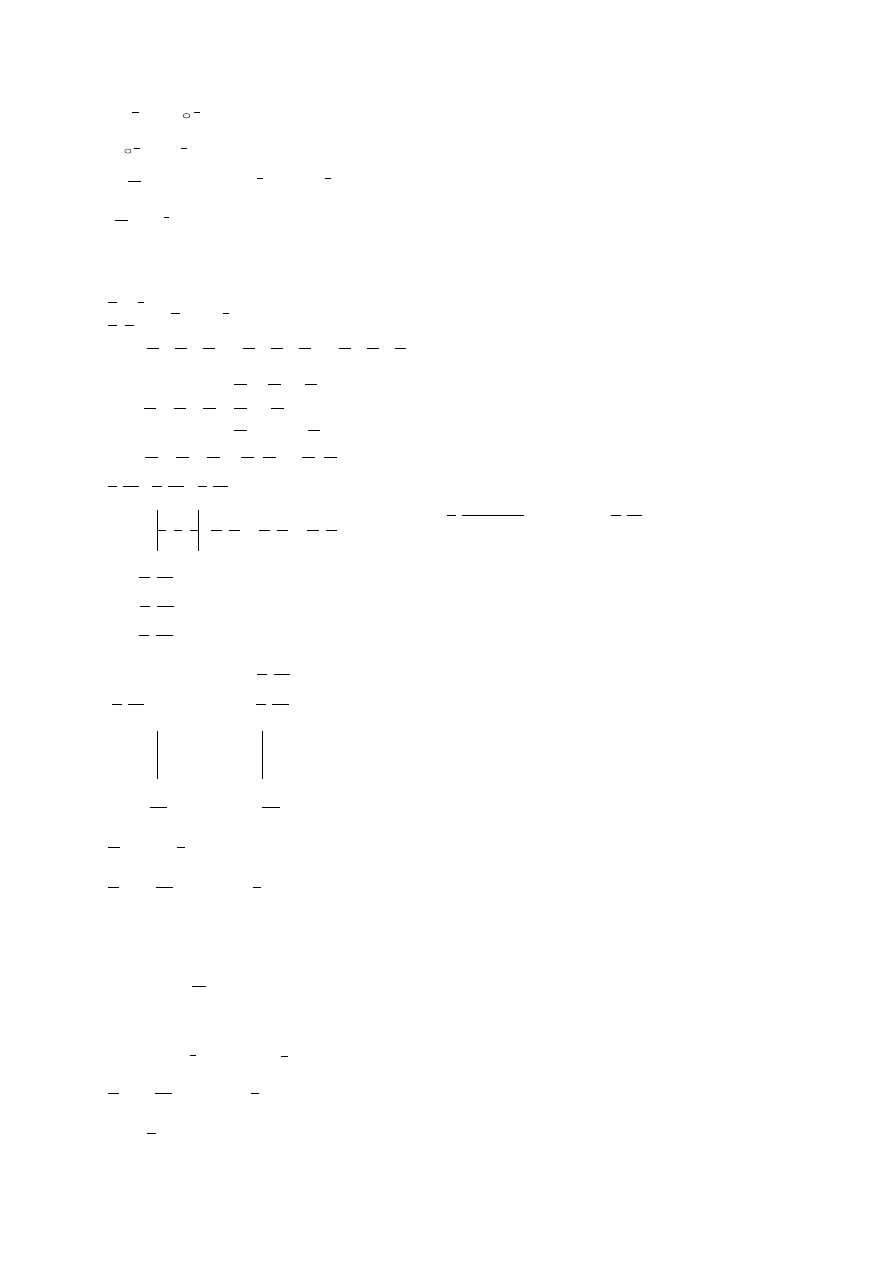
A
dA
P
A
d
P
d
Z twierdzenia Gaussa Ostrogradskiego
V
A
dV
dA
P
V
V
V
V
dV
f
dV
dV
f
P
F
dV
dt
V
d
Lokalnie mamy (Cauchy 1828)
f
dt
V
d
6.
Równanie Gromeky Lamba
p
f
v
v
dx
v
d
v
v
dx
v
d
dt
v
d
p
f
dt
v
d
1
1
k
z
v
v
y
v
v
x
v
v
j
z
v
v
y
v
v
x
v
v
i
z
v
v
y
v
v
x
v
v
v
v
z
z
z
y
z
x
y
z
y
y
y
x
x
z
x
y
x
x
Weźmy składnik na kierunek x
x
v
v
z
v
v
x
v
v
y
v
v
z
v
v
y
v
v
x
v
v
z
v
v
y
v
v
x
v
v
v
v
z
z
x
z
y
y
x
y
z
z
y
y
x
x
x
z
x
y
x
x
x
...
2
2
2
y
z
z
y
z
z
y
y
x
x
z
x
z
y
x
y
z
z
y
y
x
x
x
v
rot
v
v
rot
v
v
v
z
v
v
y
v
v
x
x
v
z
v
v
x
v
y
v
v
z
v
v
y
v
v
x
v
v
v
v
z
y
x
x
y
x
z
y
z
z
y
x
v
rot
v
rot
v
rot
k
y
v
x
v
j
z
v
x
v
i
z
v
y
v
v
v
v
z
y
x
k
j
i
v
v
rot
y
z
z
y
y
z
y
z
z
y
y
x
x
v
rot
v
v
rot
v
v
v
x
v
rot
v
rot
v
v
v
v
v
v
v
x
2
2
...
Dopisując dla składowych na kierunkach x, y, z mamy
y
z
z
y
x
v
rot
v
v
rot
v
v
v
x
v
v
2
x
z
z
x
y
v
rot
v
v
rot
v
v
v
y
v
v
2
x
y
y
x
z
v
rot
v
v
rot
v
v
v
z
v
v
2
Podstawiając do równania mamy
k
v
rot
v
v
rot
v
v
v
z
j
v
rot
v
v
rot
v
v
v
y
i
v
rot
v
v
rot
v
v
v
x
k
v
v
j
v
v
i
v
v
v
v
x
y
y
x
x
z
z
x
y
z
z
y
z
y
x
2
2
2
Rotacja rotacji prędkości
k
v
rot
v
v
rot
v
j
v
rot
v
v
rot
v
i
v
rot
v
v
rot
v
v
v
v
v
rot
v
rot
v
rot
k
j
i
v
v
rot
y
x
x
y
x
z
z
x
z
y
y
z
z
y
x
z
y
x
Więc mamy
v
v
rot
v
v
grad
v
v
v
v
v
v
2
2
Wychodząc z równania Eulera
p
f
v
v
x
v
1
Otrzymujemy równanie Gromeky-Lamba
p
grad
f
v
v
rot
v
v
grad
x
v
1
2
7.
Całki szczególne równania Gromeky Lamba
Założenia:
Przepływ jest ustalony
0
t
v
Przepływ jest bez wirowy
0
v
rot
Pole sił masowych
f
jest potencjalne
grad
f
Płyn jest barotropowy
grad
p
grad
1
d
dp
1
Wówczas równanie Gromek-Lamba
p
grad
f
v
v
rot
v
v
grad
x
v
1
2
Przyjmuje postać
grad
grad
v
grad
0
2
0
2

2
0
2
v
grad
całka Lagrangea
Izoterma
const
p
p
const
T
więc
const
p
C
p
p
p
const
p
const
dp
p
const
dp
ln
ln
ln
1
Izochora
const
C
p
const
p
dp
const
dp
1
1
Izobara
const
p
0
1
dp
Adiabata
/
1
/
1
1
1
1
1
const
p
const
p
const
p
const
p
p
C
p
p
p
const
p
p
const
p
const
dp
p
const
dp
p
const
dp
1
1
1
1
1
1
1
1
1
1
1
1
1
/
1
/
1
/
1
1
Izoterma
const
gz
p
p
v
p
p
ln
2
ln
2
Izochora
const
gz
p
v
p
2
2
Izobara
const
gz
v
2
0
2
Adiabata
const
gz
p
v
p
1
2
1
2
8.
Opory w przepływie
Równanie Bernouli’ego
0
2
2
1
2
1
2
2
2
1
z
z
g
p
p
v
v
Dla płynu rzeczywistego
e
gz
p
v
gz
p
v
2
2
2
2
1
1
2
1
2
2
Naprężenia styczne na ścianki
2
4
2
*
v
Praca płynu przeciw tarciu gdzie T to siła tarcia wywołana
*
oraz
s
u
obwód
ds
s
u
dT
*
Praca tarcia
Masa elementu strugi
dsds
s
u
x
ds
s
A
dV
dm
Odnosząc tarcie do masy
ds
s
A
s
u
ds
s
A
dsds
s
u
dm
ds
dT
x
*
*
Biorąc pod uwagę że
Oraz przyjmując że kanał jest kołowy, czyli
8
2
4
2
2
v
v
x
d
d
d
s
A
s
u
4
4
2
Elementarna strata energii
0
2
1
4
8
2
2
*
ds
v
d
ds
d
v
ds
s
A
s
u
de
Jeżeli między 1-1 a 2-2
const
to
2
2
1
2
1
2
0
2
0
2
v
d
l
ds
v
d
ds
v
d
e
l
l
Opory i straty na armaturze
Współcześnie straty energii w przepływie
2
2
v
e
n
i
i
d
l
v
e
1
2
2
9.
Podobieństwo przepływu
Równania ruchu płynu nieściśliwego
0
v
v
p
f
dt
dv
1
Wyprowadźmy skale charakterystycznych wielkości to
0
L
0
f
0
t
0
p
każdą z wielkości fizycznych można zapisać jako
x
l
x
0
y
l
y
0
z
l
z
0
t
t
t
0
…
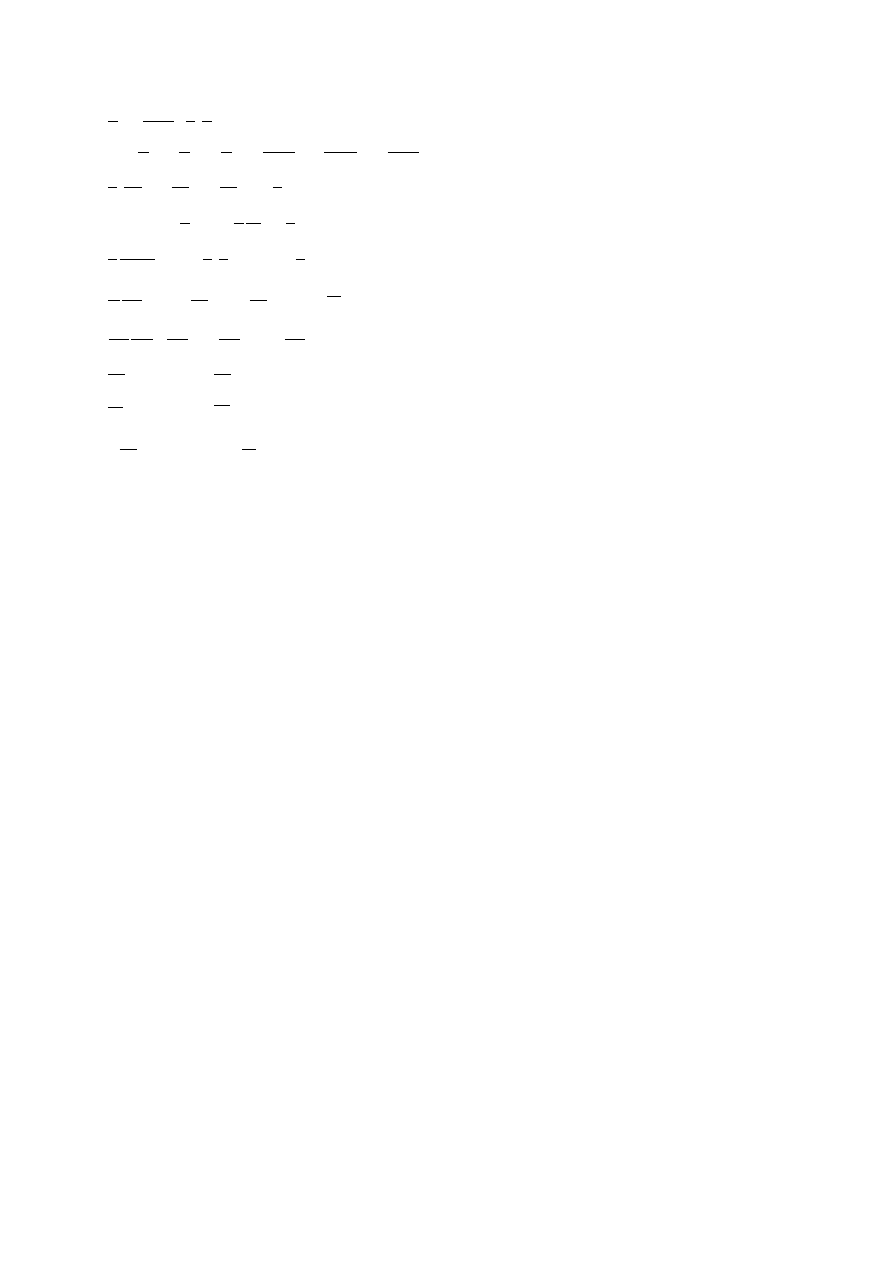
dt
d
t
t
t
d
d
dt
d
0
0
1
0
0
0
0
0
1
1
l
k
z
j
y
i
x
l
k
z
l
j
y
l
i
x
l
k
z
j
y
i
x
0
2
2
0
2
0
2
1
1
1
l
l
l
v
v
l
p
p
l
f
f
dt
v
v
d
l
0
0
0
0
0
0
0
1
1
1
1
v
l
v
p
l
p
f
f
dt
v
d
t
v
0
0
0
0
0
0
0
2
0
0
/
v
l
v
v
l
p
v
p
f
v
l
f
dt
v
d
v
t
l
0
0
2
0
0
2
0
0
0
0
0
0
St
v
t
l
0
0
0
Vincent Straud
Fr
v
l
f
2
0
0
0
William Froude
Eu
v
p
2
0
0
Leonard Euler
Re
0
0
v
l
Osborne Reynolds
Postać bezwymairowa równania Navier-Stokes
v
p
Eu
f
Fr
dt
dv
St
Re
1
Wyszukiwarka
Podobne podstrony:
sciaga MECHANIKA PLYNOW-egzamin, Inżynieria Środowiska-Szczecin, Mechanika płynów, Wykłady+kolokwia+
mechanika plynow teoria ściąga
mechanika plynow id 291486 Nieznany
mechanika plynow id 291242 Nieznany
MECHANIKA PLYNOW 1 id 291255 Nieznany
MECHANIKA PLYNOW 2(1) id 291256 Nieznany
Mechanika płynów wykład 12
mechana plynow opracowane zagadnienia kolo1, PG inżynierka, Semestr 3, Mechanika płynów, wykład
Mechanika płynów wykład 13
Mechanika płynów wykład 11
Mechanika plynow 3(1) id 291260 Nieznany
Mechanika płynów opracowane zagadnienia, Inżynieria Środowiska-Szczecin, Mechanika płynów, Wykłady+k
pytania na koło 1, PG inżynierka, Semestr 3, Mechanika płynów, wykład
KOLOKWIUM Przykłady, Politechnika Poznańska, Mechatronika, Semestr 03, Mechanika płynów - wykłady, M
MECHANIKA PLYNOW 5 id 291097 Nieznany
mechanika plynow(1) id 291208 Nieznany
Mechanika płynów Wykład nr 1, Materiały PWSZ Budownictwo, BUDOWNICTWO dodatkowe materiały, Mechanika
płyny koło sc z odp, Politechnika Poznańska, Mechatronika, Semestr 03, Mechanika płynów - wykłady, M
mechanika płynów - zadanie 3, Politechnika Poznańska (PP), Mechanika Płynów, Wykład, egzamin
więcej podobnych podstron