1

Mechanika płynów – zadania do samodzielnego rozwiązania

Zad.1. Obliczyć różnicę poziomów na jakich znajdują sie w równowadze tłoki o
powierzchniach A

1

, A

2

zamykające

pionowe rurki naczynia w kształcie litery U i obciążone

siłami P

1

, P

2

.

Zad. 2. Obliczyć nadciśnienie gazu ziemnego względem ciśnienia atmosferycznego na 12
piętrze bloku mieszkalnego (przyjąć wysokość kondygnacji 3m), jeżeli nadciśnienie na
parterze wynosi p

1

= 100 mm H

2

O. Gęstość gazu



= 0.6 kg/m

3

(pominąć zmianę gęstości

powietrza i gazu z wysokością).

Zad. 3. Barometr znajdujący sie na parterze domu wskazuje ciśnienie p

1

= 738 mm Hg. Jakie

będzie wskazanie barometru na 12 piętrze (przyjąć wysokość kondygnacji 3m)? Gęstość rteci



= 13560 kg/m

3

.

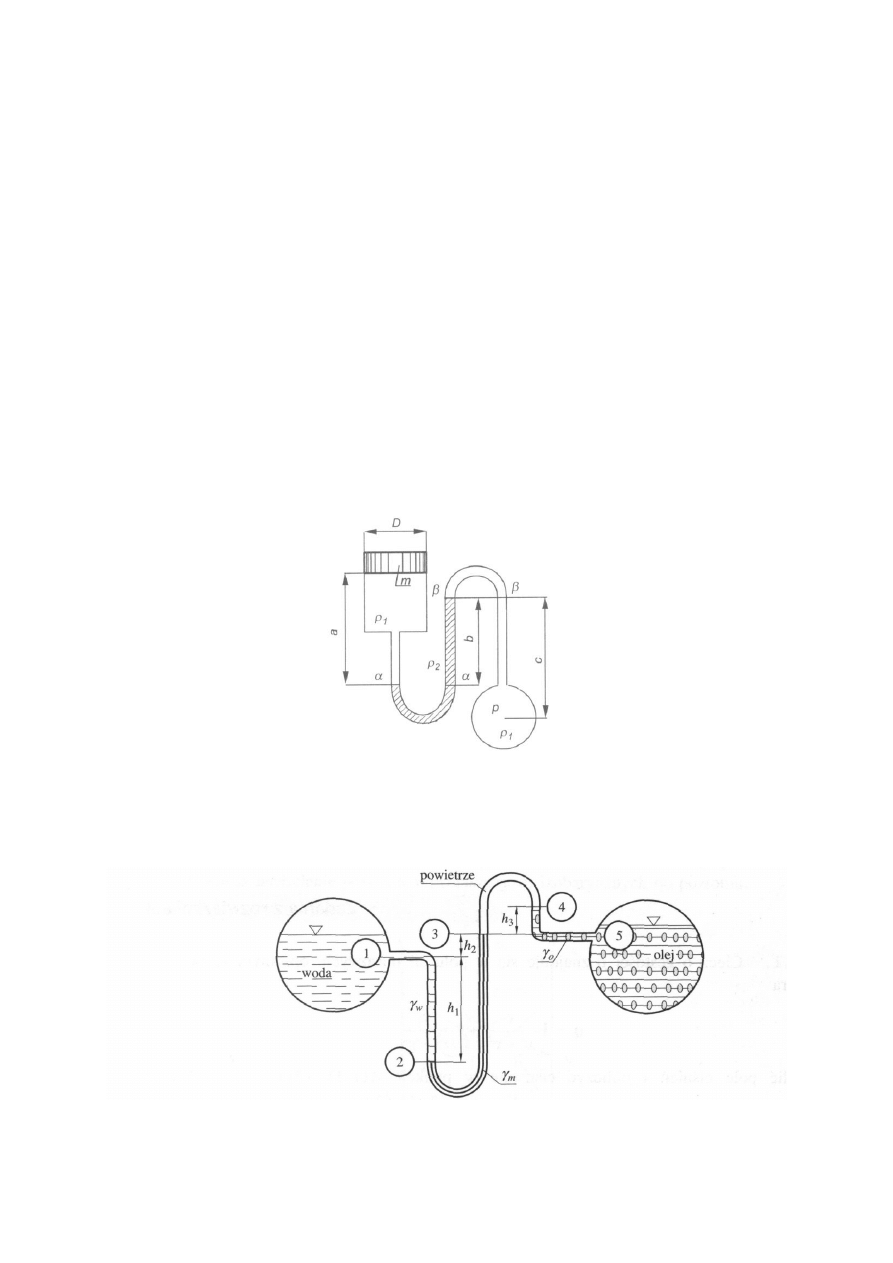
Zad. 4. Wyznaczyć ciśnienie p w prawym zbiorniku (rys.), jeżeli: masa tłoka wynosi m =
1000 kg, gęstość cieczy



1

= 1000 kg/m

3

,



2

= 2000 kg/m

3

, a = c = 2 m, b = 1.5 m, średnica

tłoka D = 1 m. Tłok porusza się bez tarcia.

Zad. 5. Pomiędzy zbiornikami z woda i olejem (o ciężarze właściwym 8830 N/m

3

)

podłączony jest manometr różnicowy, w którym kolejno są: woda, ciecz o ciężarze
właściwym 15700 N/m

3

, powietrze oraz olej. Różnice poziomów wynoszą: h

1

= 0,2 m, h

2

=

0,02 m, h

3

= 0,013m. Obliczyć różnicę ciśnienia miedzy poziomami 1 i 5 w zbiornikach.

2

Zad. 6. Manometrem podłączonym do rurociągu zmierzono nadciśnienie w miejscu jego
podłączenia. Jaki błąd popełnia sie, stosując wzór uproszczony p =



m

hg, w którym pomija

sie wpływ gęstości płynu, przy pomiarze nadciśnienia powietrza o parametrach p = 0,8 MPa i
T = 300 K. Gęstość cieczy manometrycznej (rtęci) wynosi



m

= 13600 kg/m

3

. W celu

uproszczenia przyjąć z

1

= z

3

. Rozpisać równowagę dla ramion manometru.

Zad. 7. Obliczyć różnicę ciśnień w przekrojach 1 i 2 poziomego rurociągu jeżeli manometr
różnicowy U wykazuje różnice poziomów h

m

= 100 mm, w przypadku gdy cieczą

manometryczną jest rtęć i w przypadku gdy jest nią woda.

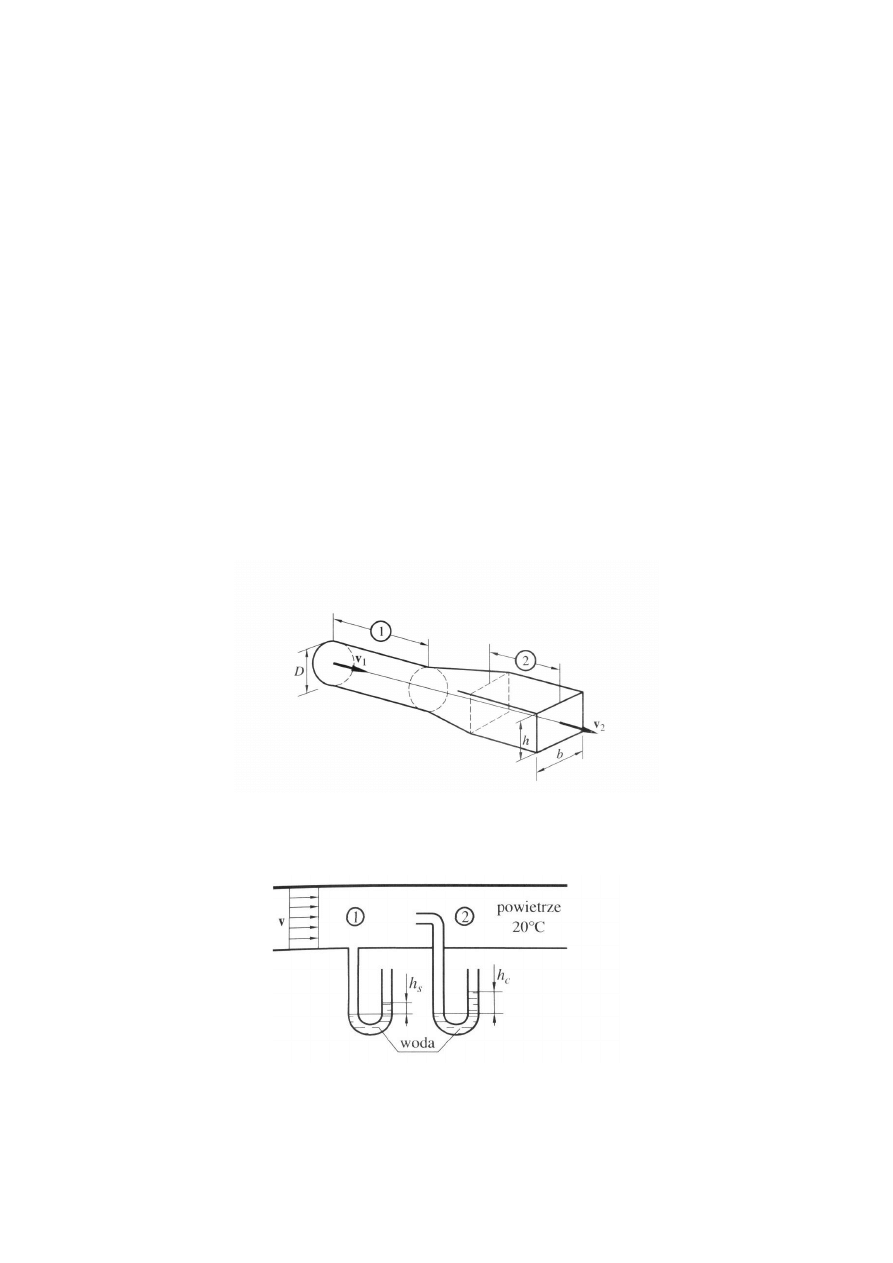
Zad. 8. Obliczyć prędkość przepływu powietrza v

1

i v

2

w dwóch przekrojach przewodu o

średnicy D

1

= 250 mm i D

2

= 80 mm, jeżeli strumień masy wynosi

m

= 0,07 kg/s. Gęstość

powietrza



= 1,2 kg/m

3

.

Zad. 9. Ile razy zmniejszy sie prędkość przepływu w przewodzie, jeżeli stosunek średnic
D2/D1=2,5 przy założeniu, że gęstość jest stała

.

Zad. 10. Przewód powietrzny składa sie z odcinka 1 o przekroju kołowym o średnicy D = 0,1
m, z odcinka pośredniego (gdzie powietrze jest podgrzewane) i z odcinka 2 o przekroju
prostokątnym b = 0,07 m, h =0,05 m. Na odcinku 1 powietrze ma temperaturę t

1

= 20

o

C i

ciśnienie bezwzględne p

1

=200 kPa, na odcinku 2 odpowiednio t

2

= 80

o

C i p

2

= 50 kPa.

Strumień masy wynosi 2 kg/s. Obliczyć prędkości powietrza na obydwu odcinkach.

Zad. 11. Powietrze o temperaturze 20

o

C płynie rurociągiem. Pierwszy manometr wodny

wskazuje różnicę poziomów h

s

= 16 mm, drugi h

c

= 24 mm. Obliczyć prędkość powietrza,

traktując go jako gaz nieściśliwy.

3

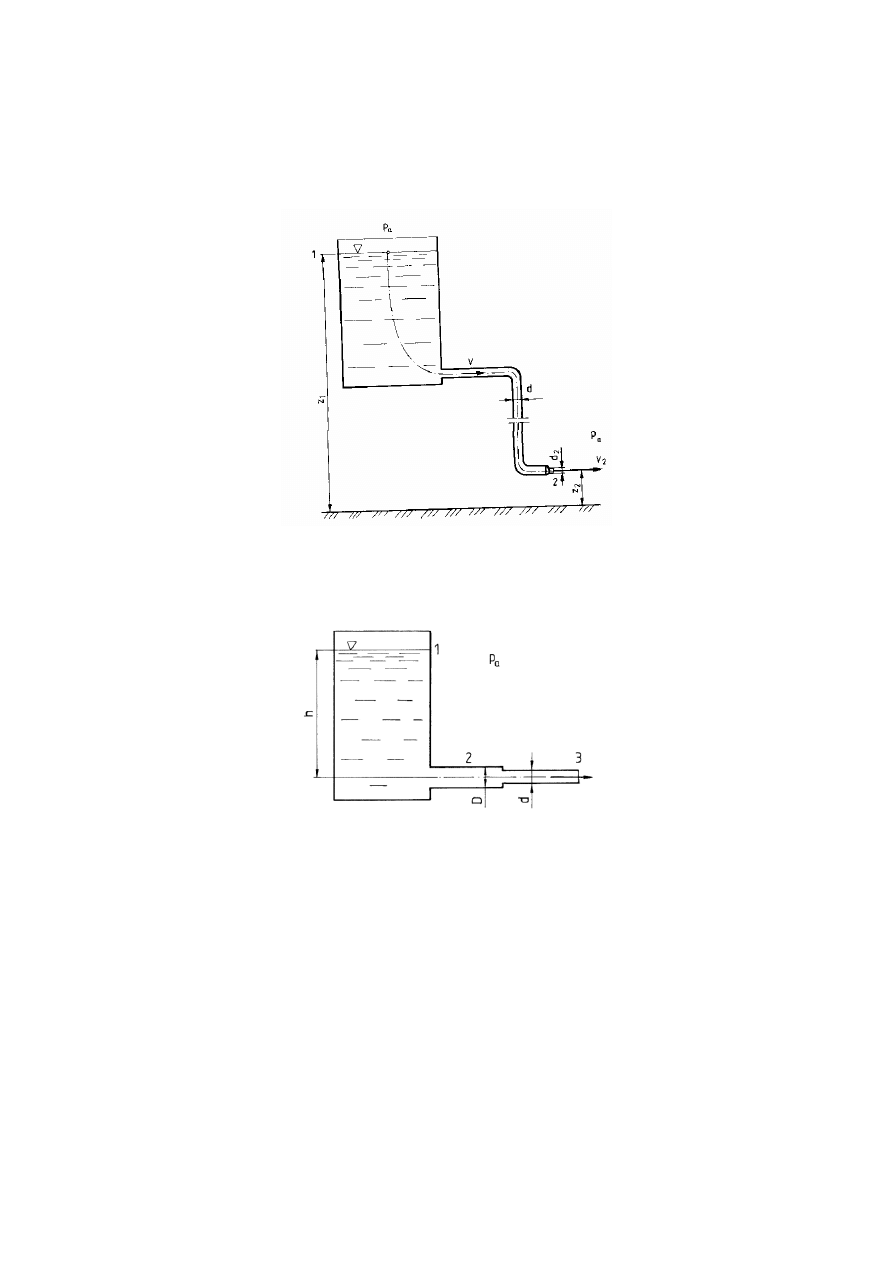
Zad. 12. Swobodna powierzchnia wody w zbiorniku otwartym o bardzo dużej średnicy jest
położona na wysokości z

1

= 50 m. Obliczyć prędkość v

2

wody na wylocie dyszy, strumień

objętości wody

•

V oraz prędkość v wody w rurociągu, jeżeli średnice rurociągu oraz dyszy

wynoszą odpowiednio d = 100 mm i d

2

= 40 mm. Wylot dyszy znajduje sie na wysokości z

2

=

5 m.

Zad. 13. Ze zbiornika wypływa woda przez kanał składający sie z dwóch odcinków o
średnicy D = 35 mm i d = 25 mm. Obliczyć prędkość wody w obu odcinkach oraz ciśnienie w
odcinku kanału o większej średnicy. Dane do zadania: h = 5 m, p

a

= 1000 hPa, średnica

zbiornika dużo większa od średnic obu odcinków.