Elementy dynamiki płynów

1. Zasada zachowania masy – równanie ciągłości przepływu

Natężeniem przepływu nazywamy ilość płynu która w jednostce czasu przepływa
przez jakąś powierzchnię. Rozważmy powierzchnię o polu A. O natężeniu
przepływu decyduje tylko normalna składowa do tej powierzchni wektora
prędkości. Ponieważ ogólnie rzecz biorąc składowa ta ma różne wartości w
różnych punktach (obraz prędkości jest polem). Wobec tego masowe natężenie
przepływu definiowane jest wzorem:

˙m=

∫

A



v

n

dA

Jednostką jest kg/s. Gdy płynem jest ciecz jednorodna (ρ=const), to:

˙m= Q

Q=

∫

A

v

n

dA

gdzie:

- jest objętościowym natężeniem przepływu lub strumieniem
objętości.Jednostką jest m

3

/s

Równanie ciągłości przepływu jest matematyczną formą prawa zachowania masy.
W obszarze który jest objęty przepływem przestrzennym, ściśliwym i nieustalonym
czyli takim że gęstość oraz prędkość są funkcjami miejsca i czasu:

=

x , y , z , t 

v=v  x , y , z , t 

I w którym nie ma źródeł masy ani upustów, wyodrębniamy obszar dV. Równanie
bilansu masy przybiera różniczkową formę równania ciągłości:

∂ 

∂

t



∂

v

x



∂

x



∂ 

v

y



∂

y



∂

v

z



∂

z

=

0

W szczególności dla płynu nieściśliwego (ρ = const) i przy wykorzystaniu
niektórych technik rachunku różniczkowego możemy napisać równanie powyższe
w postaci:

∂

v

x

∂

x



∂

v

y

∂

y



∂

v

z

∂

z

=

0

Jeżeli przepływ może być traktowany jako jednowymiarowy, czyli wszystkie
parametry przepływu zmieniają się w zależności od jednej współrzędnej (np. x)
mierzonej wzdłuż osi przepływu o zmiatającej się powierzchni A, to równanie
ciągłości możemy zapisać jako:

∂

A

∂

t



∂

Av

x



∂

x

=

0

Gdzie v

x

będzie w tym przypadku prędkością średnią w danym przekroju.

Dodatkowo jeżeli przepływ w strudze jest stacjonarny oraz nieściśliwy (ρ = const)
to możemy zapisać że dla dowolnie wybranego przekroju strugi natężenie
przepływu jest stałe:

Q=A⋅v

x

=

const

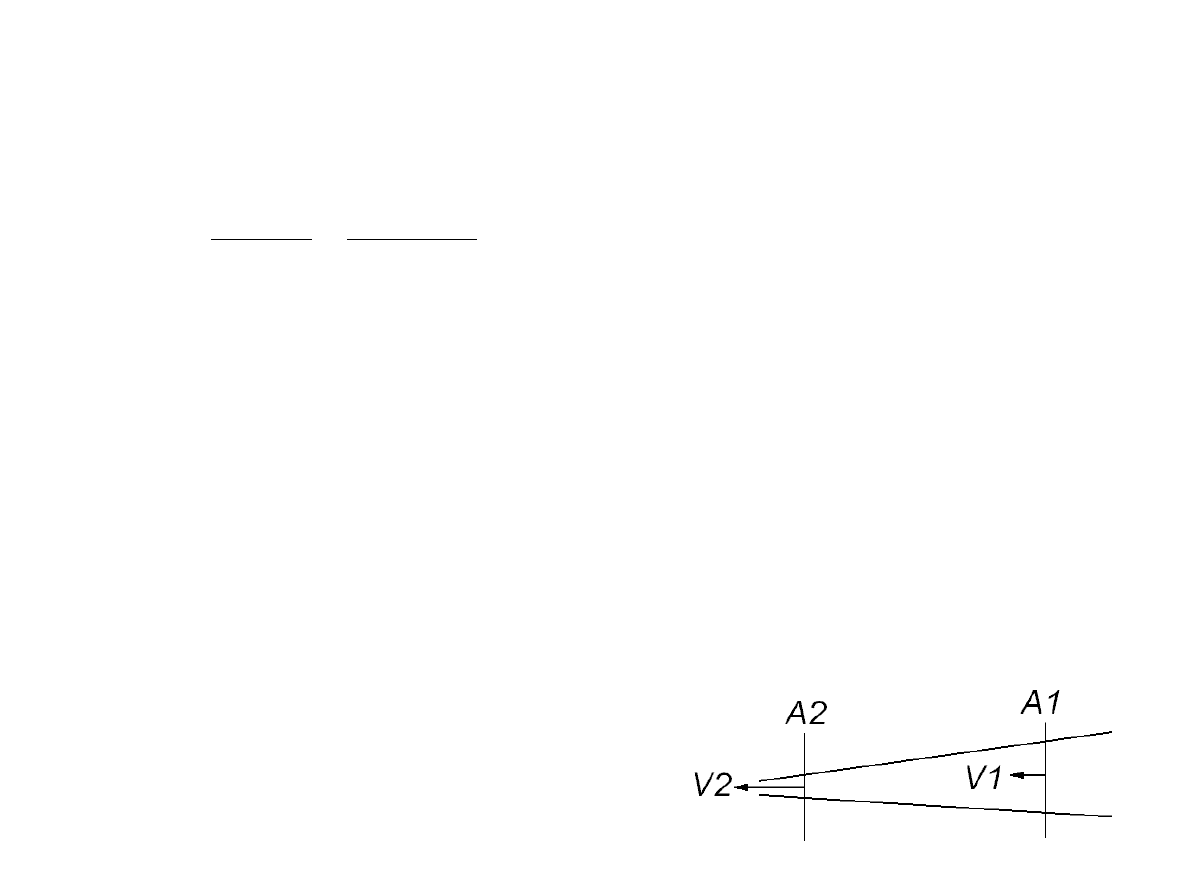
Zatem w sytuacji jak na poniższym rysunku dla przepływu przez zawężający się
obszar spełniona będzie równość:

A2⋅V2=A1⋅V1

Prędkość V2 wzrośnie w porównaniu z
prędkością V1

2. Zasada zachowania energii – równanie Bernoulliego

W rozważaniach technicznych związanych z hydrauliką bardzo szerokie
zastosowanie ma równanie Bernoulliego. Opisuje zachowanie gęstości energii
całkowitej na linii prądu. Obowiązuje ono w podstawowej wersji dla płynu
doskonałego. Założenia dla równania:

●

ciecz jest nieściśliwa

●

ciecz nie jest lepka

●

przepływ bezwirowy

Dla takich założeń możemy napisać dla każdego przekroju przepływu :

e

m

=

V

2

2



gh

p



=

const.

gdzie:

e

m

- energia jednostki masy płynu

ρ

- gęstość cieczy

v

- prędkość cieczy w rozpatrywanym miejscu

h

- wysokość w układzie odniesienia, w którym liczona jest energia

potencjalna
g

- przyspieszenie grawitacyjne

p

- ciśnienie cieczy w rozpatrywanym miejscu

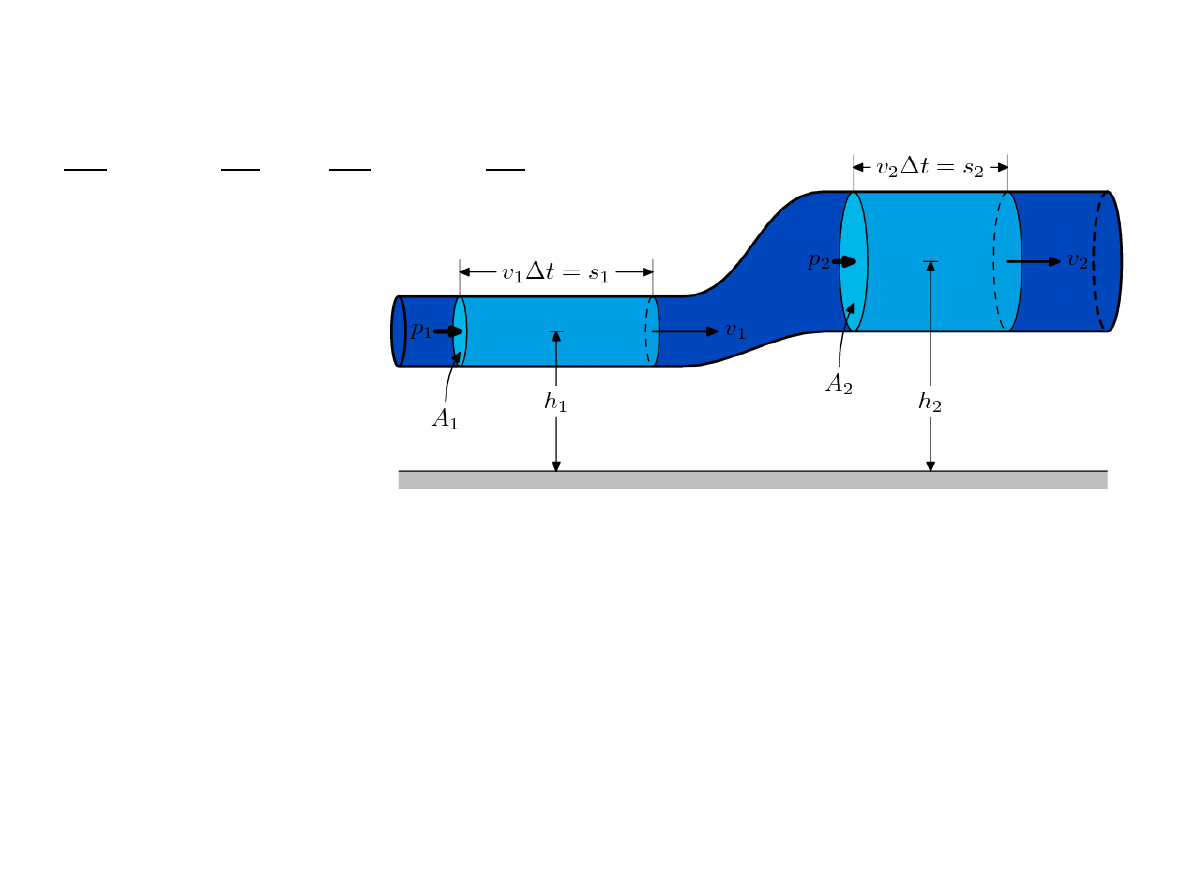
Z równania Bernoulliego dla sytuacji przedstawionej na rysunku zachodzi
prawidłowość:

V

1

2

2



gh

1



p

1



=

V

2

2

2



gh

2



p

2



W rurze o mniejszym przekroju ciecz płynie szybciej (V

1

> V

2

), w związku z tym

panuje w niej mniejsze ciśnienie niż w rurze o większym przekroju. Ciecz płynąc w
rurze o zmieniającym się przekroju ma mniejsze ciśnienie na odcinku, gdzie
przekrój jest mniejszy. Podana wyżej własność cieczy była znana przed
sformułowaniem równania przez Bernoulliego i nie potrafiono jej wytłumaczyć,
stwierdzenie to i obecnie kłóci się ze zdrowym rozsądkiem wielu ludzi i dlatego
znane jest pod nazwą paradoks hydrodynamiczny. A także: Ciecz opływając ciało
zanurzone w cieczy wywołuje mniejsze ciśnienie od strony gdzie droga przepływu
jest dłuższa.

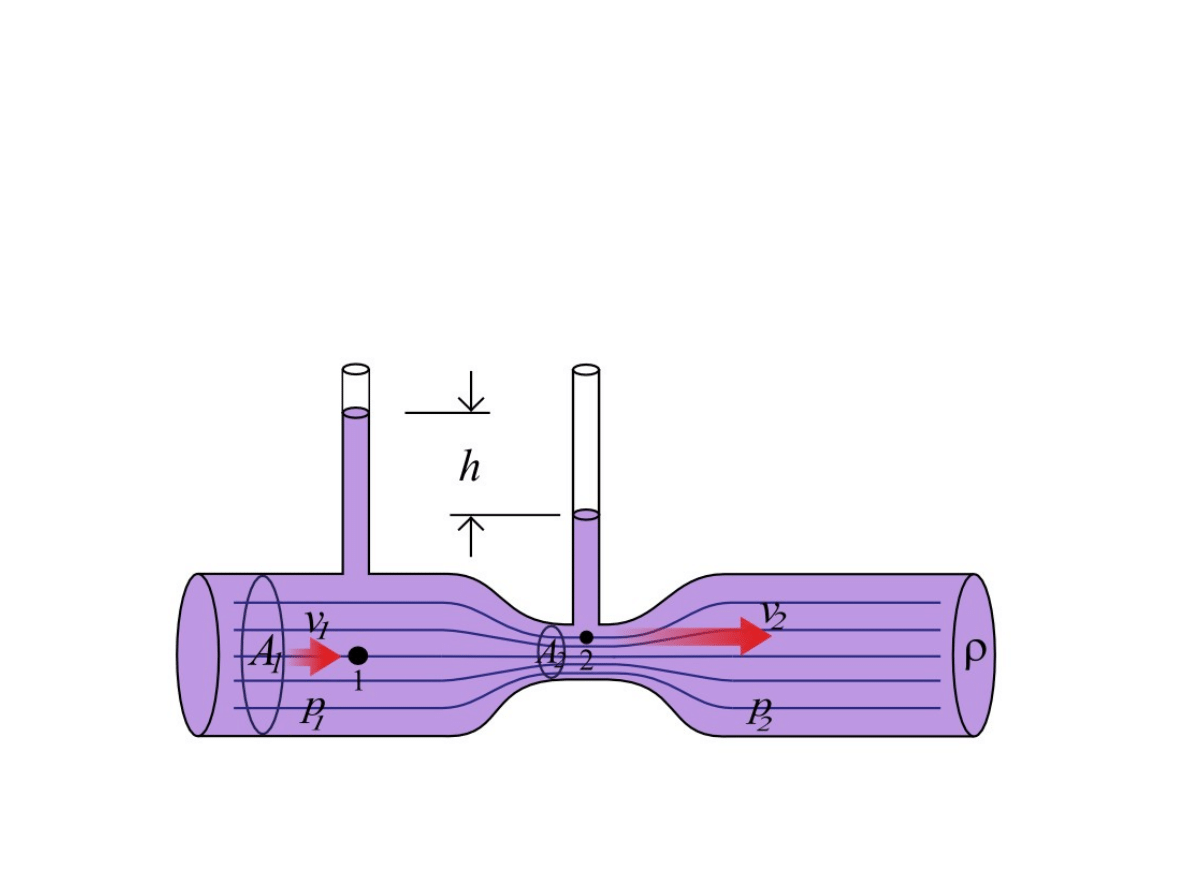
Zjawisko to wykorzystywane jest do pomiaru prędkości przepływu w tzw. zwężce
Venturiego. W pewnym miejscu kanału, w którym z prędkością V przemieszcza się
płyn (gaz lub ciecz), znajduje się przewężenie o znacznie mniejszym przekroju. Z
prawa Bernoulliego, oraz warunku ciągłości przepływu, wynika, że kwadrat
prędkości płynu przed zwężką jest wprost proporcjonalny do różnicy ciśnień
przed zwężką i na niej. Mierząc zatem różnicę wysokości h dla danego płynu
możemy obliczyć prędkość przepływu

V

1

2

2



gh

1



p

1



=

V

2

2

2



gh

2



p

2



∣

: g

Jeżeli powyższe równanie podzielimy obustronnie przez g to każdy wyraz
powyższego równania będzie miał wymiar długości (wysokości). Otrzymujemy
wówczas tzw. równanie trzech wysokości:

V

1

2

2g



h

1



p

1



=

V

2

2

2g



h

2



p

2



– ciężar właściwy płynu

V

2

2g

– nazywamy wysokością prędkości

p



– nazywamy wysokością ciśnienia



h

– nazywamy wysokością położenia (lub niwelacyjną)

W sytuacji kiedy ciecz jest lepka w przepływie występowały będą również straty
tarcia, ponadto w miejscach znacznych zmian geometrycznych w przewodzie
(zawężenie przekroju przepływu z ostrą krawędzią) występowały będą również
tzw. straty miejscowe. Równanie Bernoulliego uzupełniamy wówczas o tzw. człon
wysokości strat:

V

1

2

2g



h

1



p

1



=

V

2

2

2g



h

2



p

2





h

s

gdzie:

h

s

=

V

2

2g



- współczynnik strat wyznaczany na drodze doświadczalnej

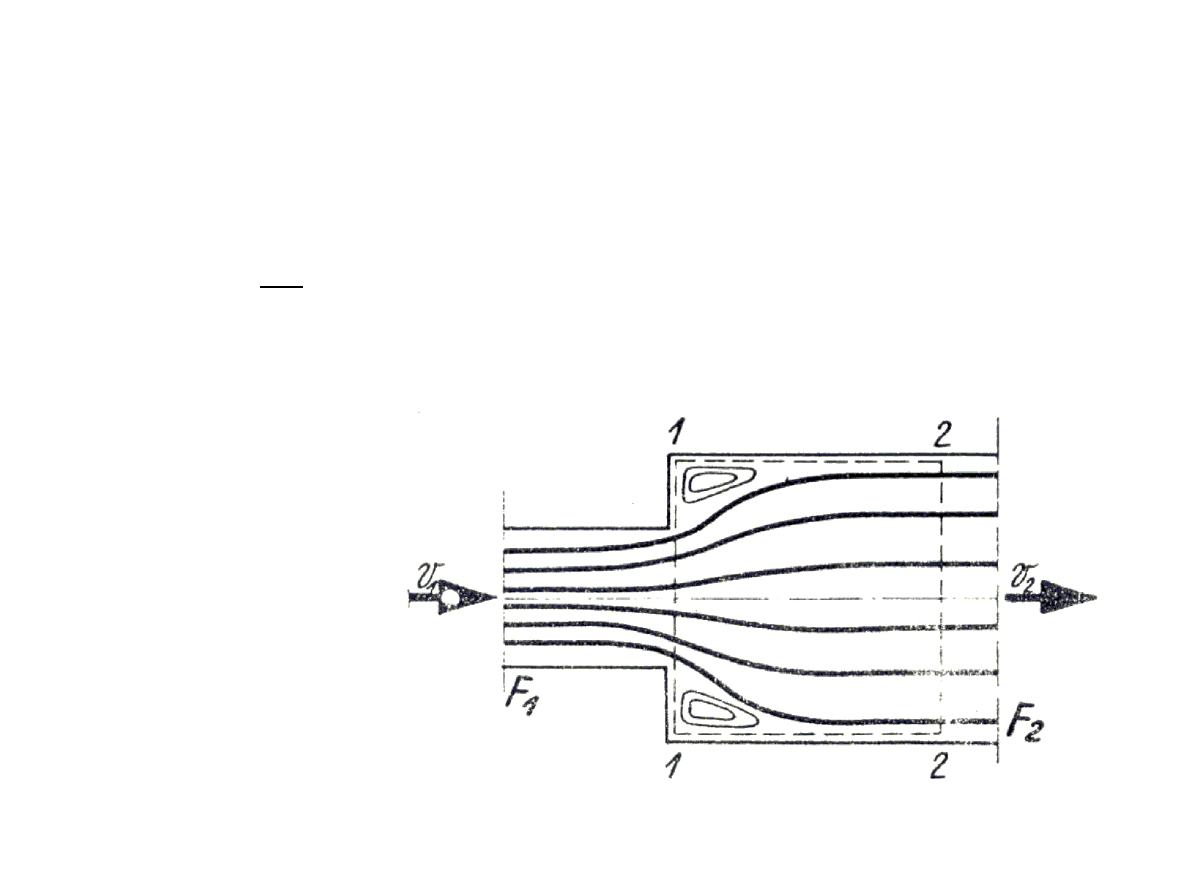
Przykład – Straty ciśnienia spowodowane zmniejszeniem się przekroju, nagłym z
ostrą krawędzią obliczamy według zależności:

=



F

2

F

1

−

1



2