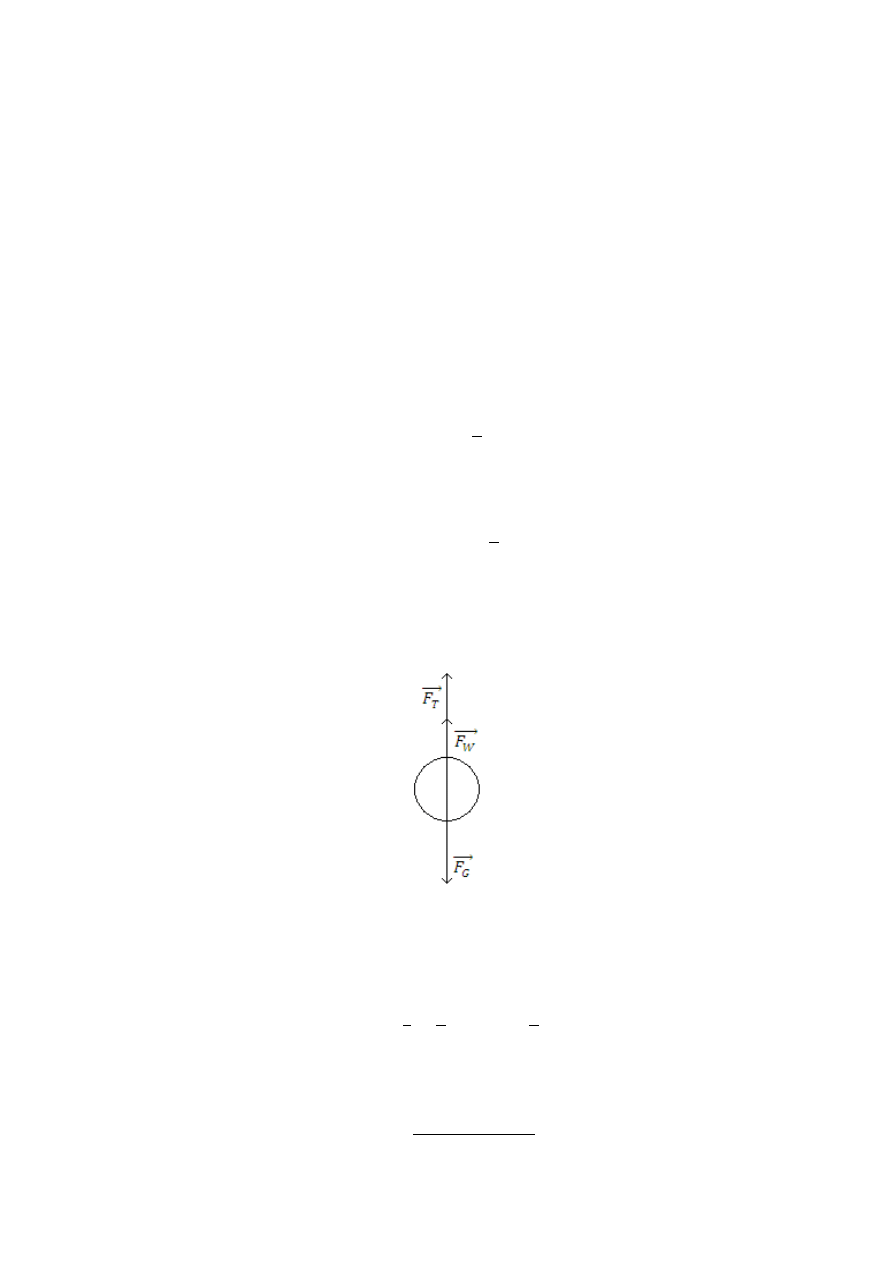
1

M16: Pomiar współczynnika lepkości cieczy metodą Stokesa.
Przemysław Kołoczek.

1. Wstęp.

Ciało zanurzone w cieczy jest pokryte warstwą tej cieczy. Gdy ciało zaczyna się poruszać w
cieczy to unosi ono ze sobą warstwę płynu, który do niej przylega, a także następne jego
warstwy na skutek tarcia wewnętrznego cieczy (lepkości). Siła tarcia (F

T

), z jaką płyn działa

na przedmiot jest dana przez prawo Stokesa:

𝐹

𝑇

= −6𝜋𝜂𝑟𝑣

Jeżeli kulka ma większą gęstość (ρ

k

) niż płyn (ρ

p

), to jej ruch zachodzi na skutek siły

ciężkości kulki (F

G

):

𝐹

𝐺

= 𝑚

𝑘

𝑔 =

4
3

𝜋𝑟

3

𝜌

𝑘

𝑔

Ponadto na kulkę działa również siła wyporu (F

W

), dana prawem Archimedesa:

𝐹

𝑊

= −𝑚

𝑝

𝑔 = −

4
3

𝜋𝑟

3

𝜌

𝑝

𝑔

Wypadkowa siła (F), działająca na kulkę wynosi:

𝐹⃗ = 𝐹

𝑇

⃗⃗⃗⃗⃗ + 𝐹

𝐺

⃗⃗⃗⃗⃗ + 𝐹

𝑊

⃗⃗⃗⃗⃗⃗

W pewnym momencie kulka porusza się ruchem jednostajnym, ze stałą prędkością v na
drodze l w czasie t, a więc F = 0 oraz na podstawie Rysunku 1.:

0 = −6𝜋𝜂𝑟

𝑙

𝑡

+

4
3

𝜋𝑟

3

𝜌

𝑘

𝑔 −

4
3

𝜋𝑟

3

𝜌

𝑝

𝑔

Po dokonaniu odpowiednich przekształceń oraz uwzględnieniu faktu, że ρ

k

= ρ

w

i ρ

p

= ρ

o

:

𝜂 =

2(𝜌

𝑤

− 𝜌

𝑜

)𝑔𝑡𝑟

2

9𝑙

Rysunek 1. Siły działające na kulkę w cieczy.

2

Ponadto należy dokonać pomiaru gęstości badanej cieczy za pomocą U-rurki:













Na granicy faz (pogrubiona linia na Rysunku 3.) zachodzi równość:

𝑚

𝑤

𝑔 = 𝑚

𝑜

𝑔

Ponieważ obie ciecze przyjmują kształt walca:

𝜌

𝑤

ℎ

𝑤

𝑆𝑔 = 𝜌

𝑜

ℎ

𝑜

𝑆𝑔

Ostatecznie:

𝜌

𝑜

= 𝜌

𝑤

ℎ

𝑤

ℎ

𝑜

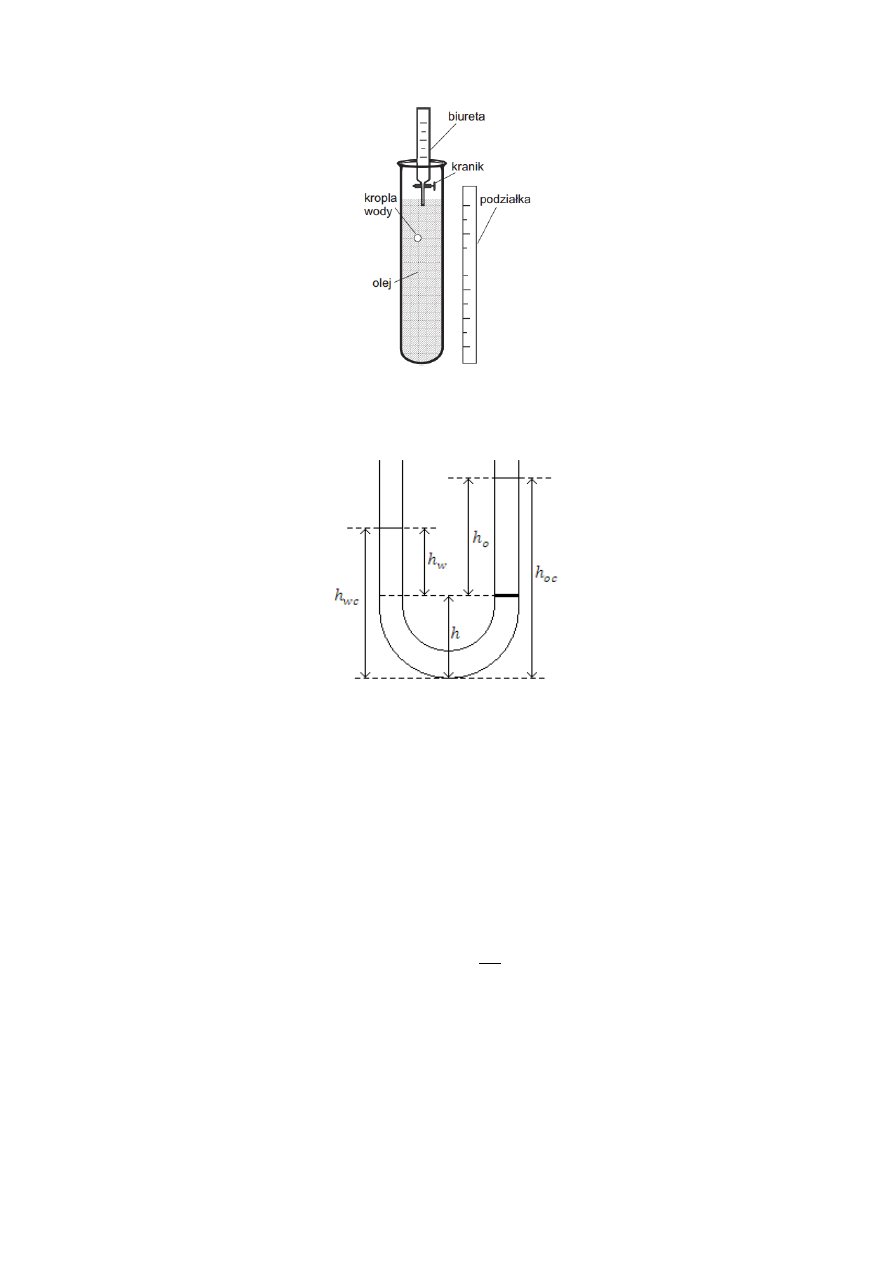
2. Opis doświadczenia.

Przygotowano zestaw do pomiaru gęstości oleju parafinowego i wyznaczono położenia
granicy faz oleju i wody, menisku wody oraz menisku oleju. Odczytano temperaturę i
gęstość wody w U-rurce. Za pomocą wkraplacza uzupełniono biuretę wodą destylowaną,
zanurzono jej końcówkę w oleju na niewielką głębokość i wyregulowano szybkość
wypływu kropel. Wybrano początek i koniec drogi na podziałce cylindra wypełnionego

Rysunek 2. Schemat układu pomiarowego lepkości oleju.

Rysunek 3. Schemat układu pomiarowego gęstości oleju.

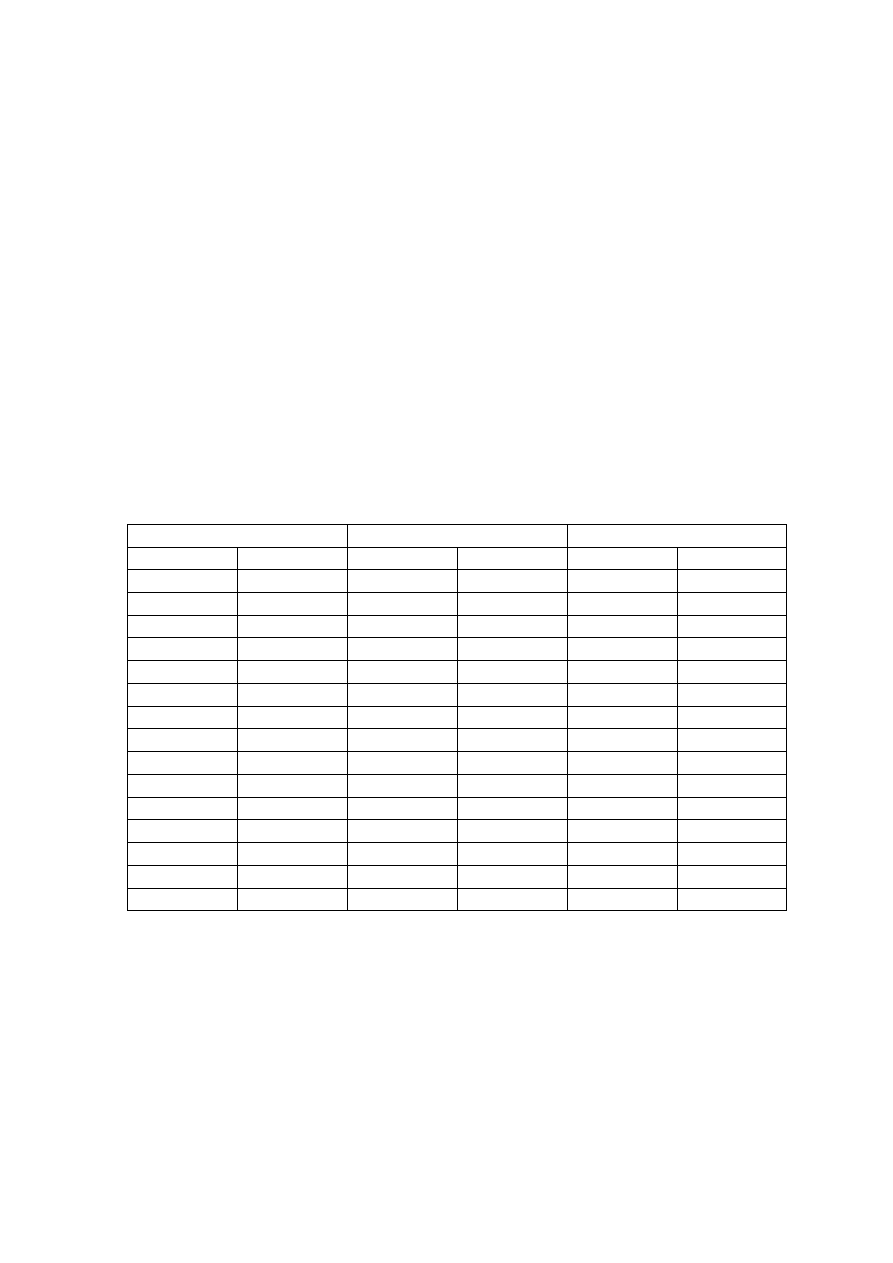
3

olejem i odczytano początkową objętość wody w biurecie. Następnie zmierzono czas
spadania kropli wody za pomocą stopera. Pomiary powtórzono dla kilku następnych
kropel wody. Biuretę ponownie uzupełniono wodą destylowaną i wszystkie czynności
powtórzono. Razem uzyskano 3 serie pomiarów.

3. Plan pracy.

a) Wlać do naczyń połączonych badaną ciecz i wodę. Wyznaczyć wysokość słupa cieczy

badanej, wody i granicy faz obu cieczy.

b) Wlać wodę do biurety, za pomocą kroplomierza.
c) Wybrać początek i koniec drogi kropli w cylindrze z badaną cieczą, wpuścić kroplę

wody do oleju i zmierzyć czas spadania kropli na ustalonej drodze.

d) Powtórzyć pomiary dla kilku następnych kropel.
e) Zanotować zużytą objętość wody w biurecie dla zaobserwowanej liczby kropel.
f) Ponownie uzupełnić biuretę wodą destylowaną za pomocą kroplomierza i ponownie

wykonać powyższe czynności.

4. Wyniki.

W wyniku przeprowadzonych analiz otrzymano następujące wyniki:

I seria

II seria

III seria

n

t [s]

n

t [s]

n

t [s]

1

46,40

1

47,59

1

45,63

2

46,22

2

47,85

2

45,34

3

46,15

3

47,19

3

45,24

4

46,35

4

47,98

4

45,16

5

46,75

5

47,75

5

45,09

6

46,22

6

47,04

6

45,13

7

46,40

7

47,88

7

45,66

8

46,62

8

47,68

8

45,65

9

46,52

9

47,53

9

45,82

10

46,02

10

47,22

10

45,00

11

46,32

11

47,44

11

45,12

12

46,03

12

47,02

12

45,03

13

46,12

13

47,00

13

45,00

14

46,32

14

47,56

14

45,12

15

46,55

15

47,38

15

45,00

Przy czym:
n – numer kropli
t – czas spadku kropli

Ponadto:

ℎ = 0,152 𝑚

∆ℎ = 0,001 𝑚

ℎ

𝑤𝑐

= 0,364 𝑚

∆ℎ

𝑤𝑐

= 0,001 𝑚

4

ℎ

𝑜𝑐

= 0,397 𝑚

∆ℎ

𝑜𝑐

= 0,001 𝑚

𝜌

𝑤

= 997,044 𝑘𝑔/𝑚

3

Dla wszystkich serii pomiarowych:

𝑉

𝑤

= 0,50 𝑐𝑚

3

∆𝑉

𝑤

= 0,05 𝑐𝑚

3

𝑙 = 0,3 𝑚

∆𝑙 = 0,01 𝑚

𝑔 = 9,81 𝑚/𝑠

2

Znaleziono wartość lepkości oleju parafinowego:

𝜂 = 0,21 𝑃𝑎 ∙ 𝑠

5. Opracowanie wyników.

Obliczono gęstość oleju na podstawie Rysunku 3. oraz poniższego wzoru:

𝜌

𝑜

= 𝜌

𝑤

ℎ

𝑤

ℎ

𝑜

= 𝜌

𝑤

(ℎ

𝑤𝑐

− ℎ)

(ℎ

𝑜𝑐

− ℎ)

gdzie:
𝜌

𝑜

– gęstość oleju [kg/m

3

],

𝜌

𝑤

– gęstość wody [kg/m

3

],

ℎ

𝑜

– wysokość słupa oleju [m],

ℎ

𝑤

– wysokość słupa wody [m],

ℎ

𝑤𝑐

– wysokość menisku wody [m],

ℎ

𝑜𝑐

– wysokość menisku oleju [m],

ℎ – wysokość granicy faz [m].

𝜌

𝑤

= 997,044 𝑘𝑔/𝑚

3

ℎ

𝑤𝑐

= 0,364 𝑚

ℎ

𝑜𝑐

= 0,397 𝑚

ℎ = 0,152 𝑚

𝜌

𝑜

= 862,748 𝑘𝑔/𝑚

3

Obliczono niepewność gęstości oleju na podstawie wzoru:

∆𝜌

𝑜

= |

𝜕𝜌

𝑜

𝜕ℎ

𝑤𝑐

∆ℎ

𝑤𝑐

| + |

𝜕𝜌

𝑜

𝜕ℎ

𝑜𝑐

∆ℎ

𝑜𝑐

| + |

𝜕𝜌

𝑜

𝜕ℎ

∆ℎ| =

2𝜌

𝑤

(ℎ

𝑤𝑐

− ℎ)

(ℎ

𝑜𝑐

− ℎ)

2

∆ℎ

oraz zależności:

∆ℎ

𝑤𝑐

= ∆ℎ

𝑜𝑐

= ∆ℎ

5

gdzie:
𝜌

𝑤

– gęstość wody [kg/m

3

],

ℎ

𝑤𝑐

– wysokość menisku wody [m],

ℎ

𝑜𝑐

– wysokość menisku oleju [m],

ℎ – wysokość granicy faz [m],
∆ℎ

𝑤𝑐

– niepewność wysokości menisku wody [m],

∆ℎ

𝑜𝑐

– niepewność wysokości menisku oleju [m],

∆ℎ – niepewność wysokości granicy faz [m].

𝜌

𝑤

= 997,044 𝑘𝑔/𝑚

3

ℎ

𝑤𝑐

= 0,364 𝑚

ℎ

𝑜𝑐

= 0,397 𝑚

ℎ = 0,152 𝑚

∆ℎ = 0,001 𝑚

∆𝜌

𝑜

= 7,043 𝑘𝑔/𝑚

3

Wynik końcowy:

𝜌

𝑜

= (862,7 ± 7,0) 𝑘𝑔/𝑚

3

Obliczono promień kropli wody na podstawie wzoru:

𝑟 = √

3𝑉

𝑤

4𝜋𝑛

3

gdzie:
𝑉

𝑤

– objętość zużytej wody, odczytana z biurety [m

3

],

𝑛 – liczba kropel, która wypłynęła z biurety.

𝑛 = 15

𝑉

𝑤

= 5 ∙ 10

−7

𝑚

3

𝑟 = 𝑟

1

= 𝑟

2

= 𝑟

3

= 0,002 𝑚

Obliczono niepewność promienia kropli wody na podstawie wzoru:

∆𝑟 = |

𝜕𝑟

𝜕𝑉

𝑤

∆𝑉

𝑤

| = √

1

36𝜋𝑛𝑉

𝑤

2

3

∆𝑉

𝑤

gdzie:
𝑉

𝑤

– objętość zużytej wody, odczytana z biurety [m

3

],

∆𝑉

𝑤

– niepewność objętość zużytej wody, odczytana z biurety [m

3

],

𝑛 – liczba kropel, która wypłynęła z biurety.

6

𝑛 = 15

𝑉

𝑤

= 5 ∙ 10

−7

𝑚

3

∆𝑉

𝑤

= 5 ∙ 10

−8

𝑚

3

∆𝑟 = ∆𝑟

1

= ∆𝑟

2

= ∆𝑟

3

= 6,7 ∙ 10

−5

𝑚

Wynik końcowy:

𝑟 = (2,00 ± 0,07) ∙ 10

−3

𝑚

Obliczono średni czas spadku kropli na podstawie wzoru:

𝑡 =

1
𝑛

∑ 𝑡

𝑖

𝑛

𝑖=1

𝑡

1

= 46,33 𝑠

𝑡

2

= 47,47 𝑠

𝑡

3

= 45,27 𝑠

Obliczono niepewność średniego czasu spadku kropli na podstawie wzoru:

∆𝑡 = ∆𝑡

𝑠𝑦𝑠

+ 𝑠

𝑡

= 0,01 + √

1

𝑛(𝑛 − 1)

∑(𝑡

𝑖

− 𝑡)

2

𝑛

𝑖=1

gdzie:
∆𝑡

𝑠𝑦𝑠

– niepewność systematyczna stopera [s],

𝑠

𝑡

– odchylenie standardowe średniego czasu spadku kropli [s].

∆𝑡

1

= 0,065 𝑠

∆𝑡

2

= 0,094 𝑠

∆𝑡

3

= 0,083 𝑠

Wyniki końcowe:

𝑡

1

= (46,33 ± 0,07) 𝑠

𝑡

2

= (47,47 ± 0,09) 𝑠

𝑡

3

= (45,27 ± 0,08) 𝑠

Obliczono lepkość oleju parafinowego na podstawie wzoru:

𝜂 =

2(𝜌

𝑤

− 𝜌

𝑜

)𝑔𝑡𝑟

2

9𝑙

7

gdzie:
𝜌

𝑜

– gęstość oleju [kg/m

3

],

𝜌

𝑤

– gęstość wody [kg/m

3

],

𝑔 – przyspieszenie ziemskie [m/s

2

],

𝑡 – średni czas spadku kropli [s],
𝑟 – promień kropli [m],
𝑙 – długość drogi spadku kropli [m].

𝜌

𝑤

= 997,044 𝑘𝑔/𝑚

3

𝜌

𝑜

= 862,748 𝑘𝑔/𝑚

3

𝑔 = 9,81 𝑚/𝑠

2

𝑟 = 0,002 𝑚

𝑙 = 0,3 𝑚
𝑡

1

= 46,33 𝑠

𝑡

2

= 47,47 𝑠

𝑡

3

= 45,27 𝑠

𝜂

1

= 0,180 𝑃𝑎 ∙ 𝑠

𝜂

2

= 0,185 𝑃𝑎 ∙ 𝑠

𝜂

3

= 0,176 𝑃𝑎 ∙ 𝑠

Obliczono niepewność lepkości oleju parafinowego na podstawie wzoru:

∆𝜂 =

4(𝜌

𝑤

− 𝜌

𝑜

)𝑔𝑡𝑟

9𝑙

∆𝑟 +

2(𝜌

𝑤

− 𝜌

𝑜

)𝑔𝑡𝑟

2

9𝑙

2

∆𝑙 +

2(𝜌

𝑤

− 𝜌

𝑜

)𝑔𝑟

2

9𝑙

∆𝑡 =

=

2𝑔𝑟(𝜌

𝑤

− 𝜌

𝑜

)(2𝑙𝑡∆𝑟 + 𝑡𝑟∆𝑙 + 𝑙𝑟∆𝑡)

9𝑙

2

gdzie:
𝜌

𝑜

– gęstość oleju [kg/m

3

],

𝜌

𝑤

– gęstość wody [kg/m

3

],

𝑔 – przyspieszenie ziemskie [m/s

2

],

𝑡 – średni czas spadku kropli [s],
𝑟 – promień kropli [m],
𝑙 – długość drogi spadku kropli [m],
∆𝑟 – niepewność promienia kropli [m],
∆𝑙 – niepewność długości drogi spadku kropli [m],
∆𝑡 – niepewność średniego czasu spadku kropli [s].

𝜌

𝑤

= 997,044 𝑘𝑔/𝑚

3

𝜌

𝑜

= 862,748 𝑘𝑔/𝑚

3

𝑔 = 9,81 𝑚/𝑠

2

𝑟 = 0,002 𝑚

𝑙 = 0,3 𝑚
∆𝑟 = 6,7 ∙ 10

−5

𝑚

∆𝑙 = 0,01 𝑚

8

𝑡

1

= 46,33 𝑠

𝑡

2

= 47,47 𝑠

𝑡

3

= 45,27 𝑠

∆𝑡

1

= 0,065 𝑠

∆𝑡

2

= 0,094 𝑠

∆𝑡

3

= 0,083 𝑠

∆𝜂

1

= 0,018 𝑃𝑎 ∙ 𝑠

∆𝜂

2

= 0,019 𝑃𝑎 ∙ 𝑠

∆𝜂

3

= 0,018 𝑃𝑎 ∙ 𝑠

Wyniki końcowe:

𝜂

1

= (0,180 ± 0,018) 𝑃𝑎 ∙ 𝑠

𝜂

2

= (0,185 ± 0,019) 𝑃𝑎 ∙ 𝑠

𝜂

3

= (0,176 ± 0,018) 𝑃𝑎 ∙ 𝑠

6. Omówienie wyników i podsumowanie.

Obliczone wartości lepkości oleju parafinowego nie są zgodne z znalezioną wartością,
równą 0,21 Pa·s. Różnią się od niej o około 0,03 Pa·s. Otrzymane wyniki lepkości oleju dla
wszystkich serii pomiarowych są równe w granicach niepewności, co świadczy o dużej
dokładności użytej metody. Z kolei na dość dobrą precyzję metody wskazuje mały rozrzut
czasów, które różnią się od siebie w obrębie danej serii (najwyżej – o niecałą sekundę).
Pomiar można usprawnić poprzez odpowiednią konserwację biuret (nasmarować
wazeliną kraniki lub nieco je obluzować, aby lżej chodziły), dzięki czemu łatwiej można by
regulować szybkość wypływu wody. Ponadto zamiast stopera i ludzkiego oka, można by
zastosować fotokomórki, które włączałby się w odpowiednim i zawsze tym samym
momencie. Największy wpływ na niepewność wielkości mierzonej miała niepewność
gęstości oleju oraz niepewność wybranej drogi przelotu kropli.

7. Literatura.

[1] A. Magiera, I Pracownia Fizyczna, IF UJ, Kraków 2010.
[2] D. Halliday, R. Resnick, J. Walker, Podstawy Fizyki 2, PWN, Warszawa 2003.
[3] J. Kobylarczyk, Pomiar współczynnika lepkości cieczy metodą Stokesa, Kraków 2013.

8. Załączniki.

Kserokopia wyników pomiarowych.