Procesor i jego architektura

(CISC, RISC, 32/64 bity).

Systemy wieloprocesorowe.

wer. 1.4

Wojciech Myszka

16 pazdziernika 2008

CISC I

Complex Instruction Set Computers

nazwa architektury

mikroprocesorów o nast¦puj¡cych cechach:

I

du»a liczba rozkazów (instrukcji)

I

maªa optymalizacja niektóre rozkazy potrzebuj¡ du»ej
liczby cykli procesora do wykonania

I

wyst¦powanie zªo»onych, specjalistycznych rozkazów

I

du»a liczba trybów adresowania

I

do pami¦ci mo»e si¦ odwoªywa¢ bezpo±rednio du»a liczba
rozkazów

I

mniejsza od RISC-ów cz¦stotliwo±¢ taktowania procesora

I

powolne dziaªanie dekodera rozkazów

CISC II

Przykªady rodzin procesorów o architekturze CISC to mi¦dzy
innymi:

I

AMD

I

x86

I

M68000

RISC I

Reduced Instruction Set Computers

I

Zredukowana liczba rozkazów do niezb¦dnego minimum.
Ich liczba wynosi kilkadziesi¡t (setki w procesorach).
Upraszcza to znacznie konstrukcj¦ procesora.

I

Redukcja trybów adresowania

wi¦kszo±¢ operacji

wykonuje si¦ wg schematu:
rejestr

C

=

rejestr

A

operacja rejestr

B

.

RISC II

I

Ograniczenie komunikacji pomi¦dzy pami¦ci¡,

a procesorem. Do przesyªania danych pomi¦dzy pami¦ci¡,

a rejestrami sªu»¡ instrukcje, które nazywaj¡ si¦ load

(zaªaduj z pami¦ci), oraz store (zapisz do pami¦ci);

pozostaªe instrukcje operuj¡ wyª¡cznie na rejestrach.

Schemat dziaªania

I

zaªaduj dan¡ z pami¦ci do rejestru,

I

na zawarto±ci rejestru wykonaj dziaªanie,

I

przepisz wynik z rejestru do pami¦ci.

I

Zwi¦kszenie liczby rejestrów (np. 32, 192, 256,

x86 jest

8), co równie» ma wpªyw na zmniejszenie liczby odwoªa«
do pami¦ci.

RISC III

I

Przetwarzanie potokowe (ang. pipelining): wszystkie
rozkazy wykonuj¡ si¦ w jednym cyklu maszynowym,
(znaczne uproszczenie bloku wykonawczego),
a zastosowanie superskalarno±ci umo»liwia równolegªe
wykonywanie rozkazów.

Superskalarno±¢

(ang. Superscalar)

mo»liwo±¢ uko«czenia

kilku instrukcji w pojedynczym cyklu zegara. Jest to mo»liwe
dzi¦ki zwielokrotnieniu jednostek wykonawczych.
Pierwszym procesorem Intela z rodziny x86 wykorzystuj¡cym
superskalarno±¢ byª procesor Pentium. Wi¦kszo±¢ procesorów
superskalarnych nie ma w peªni zduplikowanej jednostki
wykonywania kodu

mog¡ mie¢ wiele ALU, jednostek

RISC IV

zmiennopozycyjnych i tak dalej, wobec czego pewne instrukcje
b¦d¡ wykonywane bardzo szybko, a inne nie.

VLIW

Very Long Instruction Word

I

uproszczenie jednostki steruj¡cej,

I

zwi¦kszanie liczby jednostek wykonawczych,

I

technika wcze±niejszego wykonania instrukcji
(Out-of-Order Execution),

I

sterowanie prac¡ procesora zostaªo przerzucone na
kompilator (to on decyduje o sposobie dziaªania procesora).

Kompilator (ang. compiler) to program sªu»¡cy do
automatycznego tªumaczenia kodu napisanego w jednym j¦zyku
(j¦zyku ¹ródªowym) na równowa»ny kod w innym j¦zyku (j¦zyku
wynikowym)

ZISC

Zero Instruction Set Computer
Jeden z pierwszych procesorów ZISC zawieraª 36 niezale»nych
komórek (uwa»ane s¡ za neurony lub równolegªe procesory).
Ka»da z nich mo»e porówna¢ wektor wej±ciowy (64 bajty)
z podobnym wektorem przechowywanym w komórkach pami¦ci.
Je±li wektor wej±ciowy odpowiada wektorowi w komórce
pami¦ci to komórka ta wypala . Sygnaª wyj±ciowy zawiera
komórki, która miaªa dopasowanie, oraz znacznik mówi¡cy, »e
nie wyst¡piªo dopasowanie.

Schemat procesora

Rejestr (akumulator)

Pamiec (RAM)

Arytmometr

Wskazniki

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj <adres pami¦ci> przepisuje zawarto±¢ pami¦ci o
wskazanym adresie do rejestru.

I

Zapisz <adres pami¦ci> przepisuje zawarto±¢ akumulatora
do pami¦ci

I

Ładuj <liczba> zapisuje liczb¦ do rejestru

I

Dodaj <adres pami¦ci> do zawarto±ci akumulatora dodaje
zawarto±¢ komórki o wskazanym adresie (mo»emy tez
zaªo»y¢, »e w podobny sposób potra policzy¢ ró»nic¦,
iloczyn i iloraz, cho¢, w rzeczywisto±ci, nie musi to by¢
prawd¡).
Wykonanie ka»dej operacji zmieniaj¡cej zawarto±¢ rejestru
powoduje ustawienie wska¹ników (zero, przepeªnienie,
ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj <adres pami¦ci> przepisuje zawarto±¢ pami¦ci o
wskazanym adresie do rejestru.

I

Zapisz <adres pami¦ci> przepisuje zawarto±¢ akumulatora
do pami¦ci

I

Ładuj <liczba> zapisuje liczb¦ do rejestru

I

Dodaj <adres pami¦ci> do zawarto±ci akumulatora dodaje
zawarto±¢ komórki o wskazanym adresie (mo»emy tez
zaªo»y¢, »e w podobny sposób potra policzy¢ ró»nic¦,
iloczyn i iloraz, cho¢, w rzeczywisto±ci, nie musi to by¢
prawd¡).
Wykonanie ka»dej operacji zmieniaj¡cej zawarto±¢ rejestru
powoduje ustawienie wska¹ników (zero, przepeªnienie,
ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj <adres pami¦ci> przepisuje zawarto±¢ pami¦ci o
wskazanym adresie do rejestru.

I

Zapisz <adres pami¦ci> przepisuje zawarto±¢ akumulatora
do pami¦ci

I

Ładuj <liczba> zapisuje liczb¦ do rejestru

I

Dodaj <adres pami¦ci> do zawarto±ci akumulatora dodaje
zawarto±¢ komórki o wskazanym adresie (mo»emy tez
zaªo»y¢, »e w podobny sposób potra policzy¢ ró»nic¦,
iloczyn i iloraz, cho¢, w rzeczywisto±ci, nie musi to by¢
prawd¡).
Wykonanie ka»dej operacji zmieniaj¡cej zawarto±¢ rejestru
powoduje ustawienie wska¹ników (zero, przepeªnienie,
ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj <adres pami¦ci> przepisuje zawarto±¢ pami¦ci o
wskazanym adresie do rejestru.

I

Zapisz <adres pami¦ci> przepisuje zawarto±¢ akumulatora
do pami¦ci

I

Ładuj <liczba> zapisuje liczb¦ do rejestru

I

Dodaj <adres pami¦ci> do zawarto±ci akumulatora dodaje
zawarto±¢ komórki o wskazanym adresie (mo»emy tez
zaªo»y¢, »e w podobny sposób potra policzy¢ ró»nic¦,
iloczyn i iloraz, cho¢, w rzeczywisto±ci, nie musi to by¢
prawd¡).
Wykonanie ka»dej operacji zmieniaj¡cej zawarto±¢ rejestru
powoduje ustawienie wska¹ników (zero, przepeªnienie,
ujemne).

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj zmienia znak liczby w akumulatorze

I

And <adres pami¦ci> iloczyn logiczny (bit po bicie dwu sªów)

I

Or <adres pami¦ci>

I

Xor <adres pami¦ci>

ró»nica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje steruj¡ce

I

Skocz <adres pami¦ci> bezwarunkowe przekazanie
sterowanie do adresu

I

Skocz_jezeli_zero <adres pami¦ci>

I

Skocz_jezeli_ujemne <adres pami¦ci>

I

Skocz_jesli_nadmiar <adres pami¦ci>

I

Skocz_do_podprogramu <adres pami¦ci> bardzo podobne do
instrukcji zwykªego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pami¦ci

Podstawowe operacje

Instrukcje steruj¡ce

I

Skocz <adres pami¦ci> bezwarunkowe przekazanie
sterowanie do adresu

I

Skocz_jezeli_zero <adres pami¦ci>

I

Skocz_jezeli_ujemne <adres pami¦ci>

I

Skocz_jesli_nadmiar <adres pami¦ci>

I

Skocz_do_podprogramu <adres pami¦ci> bardzo podobne do
instrukcji zwykªego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pami¦ci

Podstawowe operacje

Instrukcje steruj¡ce

I

Skocz <adres pami¦ci> bezwarunkowe przekazanie
sterowanie do adresu

I

Skocz_jezeli_zero <adres pami¦ci>

I

Skocz_jezeli_ujemne <adres pami¦ci>

I

Skocz_jesli_nadmiar <adres pami¦ci>

I

Skocz_do_podprogramu <adres pami¦ci> bardzo podobne do
instrukcji zwykªego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pami¦ci

Podstawowe operacje

Instrukcje steruj¡ce

I

Skocz <adres pami¦ci> bezwarunkowe przekazanie
sterowanie do adresu

I

Skocz_jezeli_zero <adres pami¦ci>

I

Skocz_jezeli_ujemne <adres pami¦ci>

I

Skocz_jesli_nadmiar <adres pami¦ci>

I

Skocz_do_podprogramu <adres pami¦ci> bardzo podobne do
instrukcji zwykªego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pami¦ci

Podstawowe operacje

Instrukcje steruj¡ce

I

Skocz <adres pami¦ci> bezwarunkowe przekazanie
sterowanie do adresu

I

Skocz_jezeli_zero <adres pami¦ci>

I

Skocz_jezeli_ujemne <adres pami¦ci>

I

Skocz_jesli_nadmiar <adres pami¦ci>

I

Skocz_do_podprogramu <adres pami¦ci> bardzo podobne do
instrukcji zwykªego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pami¦ci

Asembler

Bardzo proste dziaªanie:
A=B+C

W komórce o adresie A ma by¢ umieszczony wynik dodawania
zawarto±ci komórek o adresie B i C.
Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

Asembler

Bardzo proste dziaªanie:
A=B+C
W komórce o adresie A ma by¢ umieszczony wynik dodawania
zawarto±ci komórek o adresie B i C.

Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

Asembler

Bardzo proste dziaªanie:
A=B+C
W komórce o adresie A ma by¢ umieszczony wynik dodawania
zawarto±ci komórek o adresie B i C.
Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

MARIE

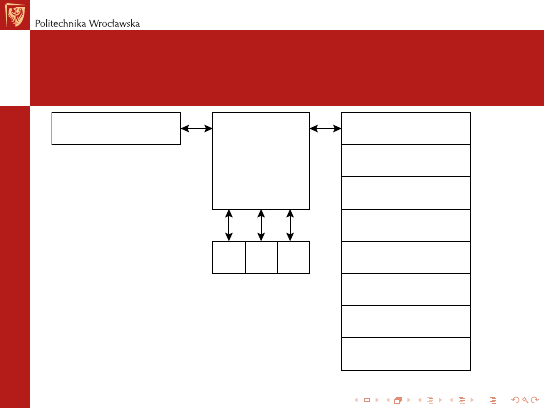
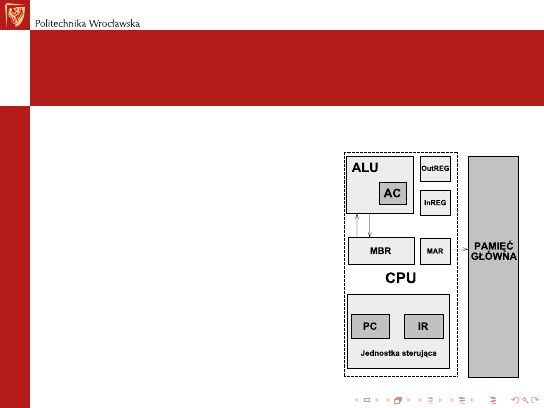
MARIE

A Machine Architecture that is Really Intuitive and Easy

I

notacja dwójkowa, zapis w kodzie dopeªnieniowym

I

przechowywanie programu, staªa dªugo±¢ sªowa

I

adresowanie sªowne

I

4K pami¦ci gªównej (12 bitów na ka»dy adres)

I

16-bitowe dane (16-bitowe sªowa)

I

16-bitowe rozkazy (4-bitowy kod operacji + 12-bitowy adres)

I

16-bitowy akumulator (AC)

I

16-bitowy rejestr rozkazów (IR)

I

16-bitowy rejestr bufora pami¦ci (MBR)

I

12-bitowy licznik rozkazów (PC)

I

12-bitowy rejestr adresów pami¦ci (MAR)

I

8-o bitowy rejestr wej±ciowy (InREG)

I

8-o bitowy rejestr wyj±ciowy (OutREG)

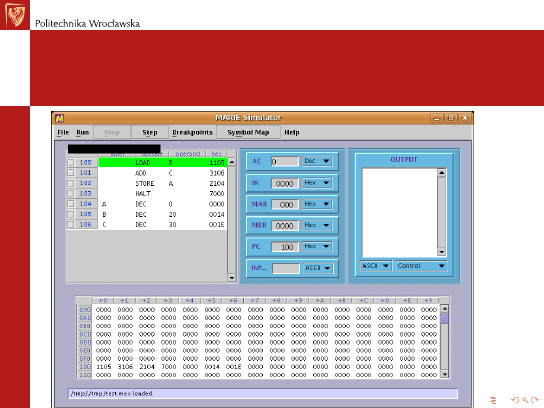
Symulator MARIE

Asembler

Bardziej skomplikowany przykªad

Z =

[(

A + B)(C + D)]

W

T1 = A + B
T2 = C + D
T3 = T1 ∗ T2
Z = T3/W

Asembler

Bardziej skomplikowany przykªad

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D
T3 = T1 ∗ T2
Z = T3/W

Asembler

Bardziej skomplikowany przykªad

Z =

[(

A + B)(C + D)]

W

T1 = A + B
T2 = C + D

T3 = T1 ∗ T2
Z = T3/W

Asembler

Bardziej skomplikowany przykªad

Z =

[(

A + B)(C + D)]

W

T1 = A + B
T2 = C + D
T3 = T1 ∗ T2

Z = T3/W

Asembler

Bardziej skomplikowany przykªad

Z =

[(

A + B)(C + D)]

W

T1 = A + B
T2 = C + D
T3 = T1 ∗ T2
Z = T3/W

Odwrotna Notacja Polska

Popatrzmy na dziaªanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak ªatwo znale¹¢ kalkulator który liczy ¹le ?

Odwrotna Notacja Polska

Popatrzmy na dziaªanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak ªatwo znale¹¢ kalkulator który liczy ¹le ?

Odwrotna Notacja Polska

Popatrzmy na dziaªanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?

Czemu tak ªatwo znale¹¢ kalkulator który liczy ¹le ?

Odwrotna Notacja Polska

Popatrzmy na dziaªanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak ªatwo znale¹¢ kalkulator który liczy ¹le ?

Wa»no±¢ dziaªa« arytmetycznych

1.

pot¦gowanie

2.

mno»enie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mog¡ j¡ zmienia¢!

Wa»no±¢ dziaªa« arytmetycznych

1.

pot¦gowanie

2.

mno»enie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mog¡ j¡ zmienia¢!

Wa»no±¢ dziaªa« arytmetycznych

1.

pot¦gowanie

2.

mno»enie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mog¡ j¡ zmienia¢!

Czy jest mo»liwy zapis jednoznaczny?

Polski logik, Šukasiewicz, wprowadziª notacj¦ przedrostkow¡ .
Zamiast z = x + y zaproponowaª zapis:

+

xy

Zwracam uwag¦ »e jest on bardzo podobny do zapisu funkcji
dwu zmiennych:

z = f(x, y)

Funkcja suma jest te» dwuargumentowa:

z = +(x, y)

Czy jest mo»liwy zapis jednoznaczny?

Polski logik, Šukasiewicz, wprowadziª notacj¦ przedrostkow¡ .
Zamiast z = x + y zaproponowaª zapis:

+

xy

Zwracam uwag¦ »e jest on bardzo podobny do zapisu funkcji
dwu zmiennych:

z = f(x, y)

Funkcja suma jest te» dwuargumentowa:

z = +(x, y)

Zapis polski

Dziaªanie 3 + 7 × 5 oznaczaj¡ce 3 + (7 × 5) zapisujemy:

+ ×

7 5

| {z }

3

|

{z

}

odwrotny zapis polski

Utarªo si¦ u»ywanie innego zapisu: najpierw podaje si¦
argumenty dziaªania, pó¹niej samo dziaªanie:

xy+

St¡d nazwa: Odwrotna notacja polska .
Nasze dziaªanie zapisujemy tak:

7 5 × 3+

a to bardziej skomplikowane tak:

A B + C D + ×W /

Odwrotna Notacja Polska

stos

Praktyczna realizacja dziaªania

A B + C D + ×W /

wymaga stosu. I dodatkowych operacji w j¦zyku wewn¦trznym:

I

Zapisz_na_stos przepisuje zawarto±¢ akumulatora na stos.

I

Pobierz_ze_stosu pobiera ze stosu warto±¢ i przepisuje j¡
do akumulatora

Stos

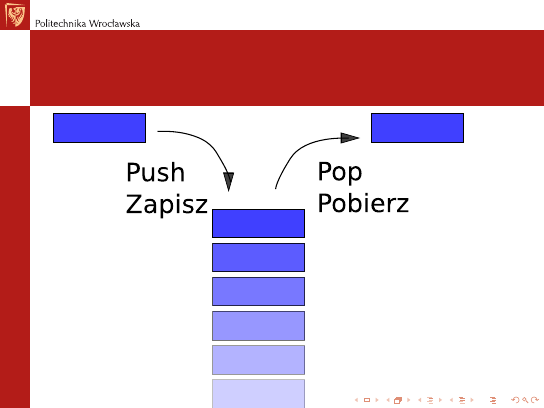
Stos

Prosty kalkulator

http://www.calculator.org

Praktyczna realizacja dziaªania

A B + C D + ×W /

A = 1, B = 2, C = 3, D = 4, W = 5

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb

dwójkowy.

I

Ka»da z liczb zapisywana jest za pomoc¡ cyfr 0 i 1.

I

Ukªad jest pozycyjny

waga cyfry zale»y od miejsca,

w którym zostaªa ustawiona.

I

Najmniej znacz¡ce miejsca s¡ po stronie prawej. . .

I

1010 to 1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli 8 + 0 + 2 + 0 = 10

I

NB liczby parzyste maj¡ zero na ko«cu, nieparzyste

1.

I

Arytmetyka dwójkowa

bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

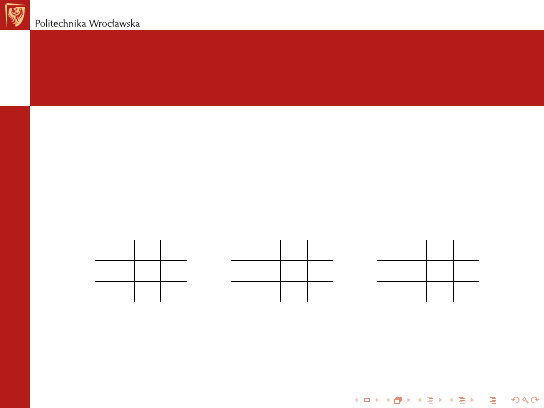
Operacje logiczne

(Podstawowe) operacje logiczne to suma logiczna (OR), iloczyn
logiczny (AND), negacja (NOT), ró»nica symetryczna (XOR)

OR 0 1

0 0 1
1 1 1

AND 0 1

0 0 0
1 0 1

XOR 0 1

0 0 1
1 1 0

Arytmetyka komputera

Arytmetyka klasyczna

Jeste±my przyzwyczajeni do nast¦puj¡cych rzeczy :

1.

Je»eli x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powy»sze zasady nie obowi¡zuj¡!

Arytmetyka komputera

Arytmetyka klasyczna

Jeste±my przyzwyczajeni do nast¦puj¡cych rzeczy :

1.

Je»eli x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powy»sze zasady nie obowi¡zuj¡!

Arytmetyka komputera

Arytmetyka klasyczna

Jeste±my przyzwyczajeni do nast¦puj¡cych rzeczy :

1.

Je»eli x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powy»sze zasady nie obowi¡zuj¡!

Arytmetyka komputera

Arytmetyka klasyczna

Jeste±my przyzwyczajeni do nast¦puj¡cych rzeczy :

1.

Je»eli x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powy»sze zasady nie obowi¡zuj¡!

Liczby zmiennoprzecinkowe

1.

Arytmetyka

1.1

Liczby naturalne

1.2

Liczby caªkowite

1.3

Liczby wymierne

1.4

Liczby rzeczywiste

2.

Komptery

2.1

Liczby caªkowite ( integer )

2.2

Liczby staªoprzecinkowe

2.3

Liczby zmiennoprzecinkowe

Liczby caªkowite I

I

Sytuacja dosy¢ klarowna.

I

Na n bitach mo»emy zapisa¢ liczby caªkowite dodatnie z
zakresu od zera do 2

n

−

1

I

Jest pewien problem z liczbami ujemnymi: trzeba
zarezerwowa¢ miejsce na znak

I

Trzeba to tak zrobi¢, »eby podstawowe operacje
(dodawanie, odejmowanie i mno»enie,. . . ) byªy
wykonywane tak samo gdy argumenty s¡ dodatnie jak i
wtedy gdy s¡ ujemne.

I

Ukªad uzupeªnieniowy to zaªatwiª.

Liczby caªkowite II

I

Czasami korzysta si¦ z kodu BCD (Binary Coded Decimal
(cyfry) dziesi¦tne kodowane binarnie: liczba zapisywana
jest w ukªadzie dziesi¦tnym (za pomoc¡ cyfr dziesi¦tnych),
ale poszczególne cyfry kodowane s¡ binarnie
321

(

10)

zapisywane jest jako 0011 0010 0001

2

Liczby staªoprzecinkowe

1.

Liczby w których na zapami¦tanie cz¦±ci caªkowitej
przeznacza si¦ kilka(na±cie/dziesi¡t) bitów

2.

Na zapami¦tanie cz¦±ci uªamkowej równie» u»ywa si¦
kilku(nastu?) bitów:

1 0 1 0 , 1 0 1 0

co odczytujemy jako:
1∗2

3

+

0∗2

2

+

1∗2

1

+

0∗2

0

+

1∗2

−

1

+

0∗2

−

2

+

1∗2

−

3

+

0∗2

−

4

lub 8 + 2 +

1

2

+

1

8

czyli 10,625

3.

U»ywany bardzo rzadko ( nanse??)

4.

Z matematycznego punktu widzenia s¡ to liczby wymierne

5.

Jak w tej postaci zapisa¢ liczb¦ 1,1

Liczby zmiennoprzecinkowe I

1.

S¡ to liczby zapisywane (kodowane) w sposób podobny do
zananego nam: c = 299792458 ∼ 3 ∗ 10

8

m/s

2.

Czyli w postaci mantysa (2,99792458) plus wykªadnik 8,
zatem 2,99792458*10

8

albo inaczej 2,99792458 e8

3.

W przypadku komputerów podstawa kodowania (tak
mantysy jak i wykªadnika) to 2!

4.

Dodatkowo liczby zapisywane s¡ zawsze w postaci

znormalizowanej czyli takiej, »e cyfra przed przecinkiem

(kropk¡) dziesi¦tnym jest zawsze z zakresu mi¦dzy 1 a 9. (a
w ukªadzie dwójkowym zawsze jest równa 1!)

5.

Na zapami¦tanie mantysy i wykªadnika przeznaczana jest
zawsze sko«czona liczba bitów.

Liczby zmiennoprzecinkowe II

6.

Z matematycznego punktu widzenia s¡ to liczby wymierne.

7.

Sposób zapisu liczb zmiennoprzecinkowych reguluje
standard IEE-754.

Par¦ problemów

1.

Zawsze(?) ograniczona liczba bitów przeznaczona na
zapami¦tanie liczby (ale znane s¡ specjalne programy,
które staraj¡ si¦ te ograniczenie przezwyci¦»a¢).

2.

Wynik dziaªa« arytmetycznych cz¦sto prowadzi do
powstania nadmiaru (czyli przekroczenia maksymalnej
dopuszczalnej warto±ci liczb).

3.

Wi¦kszo±¢ liczb który (z przyzwyczajenia) traktujemy jako
dokªadne nie ma dokªadnej reprezentacji dwójkowej (0,5
jest OK ale 0,1 ju» nie.