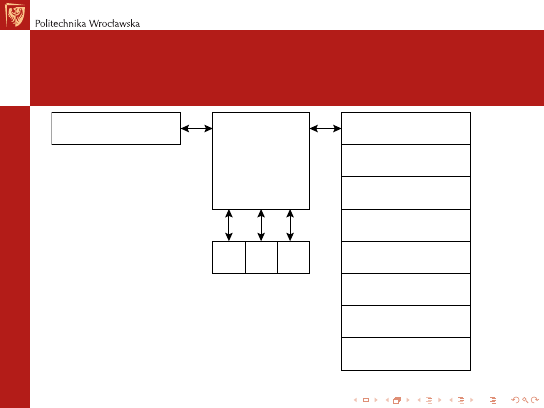
Procesor i jego architektura

(CISC, RISC, 32/64 bity).

Systemy wieloprocesorowe.

Wojciech Myszka

14 października 2011

CISC I

Complex Instruction Set Computers — nazwa architektury
mikroprocesorów o następujących cechach:

I

duża liczba rozkazów (instrukcji)

I

mała optymalizacja – niektóre rozkazy potrzebują dużej liczby
cykli procesora do wykonania

I

występowanie złożonych, specjalistycznych rozkazów

I

duża liczba trybów adresowania

I

do pamięci może się odwoływać bezpośrednio duża liczba
rozkazów

I

mniejsza od RISC-ów częstotliwość taktowania procesora

I

powolne działanie dekodera rozkazów

CISC II

Przykłady rodzin procesorów o architekturze CISC to między
innymi:

I

AMD

I

x86

I

M68000

RISC I

Reduced Instruction Set Computers

I

Zredukowana liczba rozkazów do niezbędnego minimum. Ich
liczba wynosi kilkadziesiąt (setki w procesorach). Upraszcza to
znacznie konstrukcję procesora.

I

Redukcja trybów adresowania — większość operacji wykonuje
się wg schematu:

rejestr

C

=

rejestr

A

operacja rejestr

B

.

I

Ograniczenie komunikacji pomiędzy pamięcią, a procesorem.
Do przesyłania danych pomiędzy pamięcią, a rejestrami służą
instrukcje, które nazywają się load (załaduj z pamięci), oraz
store (zapisz do pamięci); pozostałe instrukcje operują
wyłącznie na rejestrach. Schemat działania

I

załaduj daną z pamięci do rejestru,

RISC II

I

na zawartości rejestru wykonaj działanie,

I

przepisz wynik z rejestru do pamięci.

I

Zwiększenie liczby rejestrów (np. 32, 192, 256, — x86 jest 8),
co również ma wpływ na zmniejszenie liczby odwołań do
pamięci.

I

Przetwarzanie potokowe (ang. pipelining): wszystkie rozkazy
wykonują się w jednym cyklu maszynowym, (znaczne
uproszczenie bloku wykonawczego), a zastosowanie
superskalarności umożliwia równoległe wykonywanie rozkazów.

RISC III

Superskalarność — (ang. Superscalar) — możliwość ukończenia
kilku instrukcji w pojedynczym cyklu zegara. Jest to możliwe dzięki
zwielokrotnieniu jednostek wykonawczych.
Pierwszym procesorem Intela z rodziny x86 wykorzystującym
superskalarność był procesor Pentium. Większość procesorów
superskalarnych nie ma w pełni zduplikowanej jednostki
wykonywania kodu — mogą mieć wiele ALU, jednostek
zmiennopozycyjnych i tak dalej, wobec czego pewne instrukcje będą
wykonywane bardzo szybko, a inne nie.

VLIW

Very Long Instruction Word

I

uproszczenie jednostki sterującej,

I

zwiększanie liczby jednostek wykonawczych,

I

technika wcześniejszego wykonania instrukcji (Out-of-Order
Execution),

I

sterowanie pracą procesora zostało przerzucone na kompilator
(to on decyduje o sposobie działania procesora).

Kompilator (ang. compiler) to program służący do automatycznego
tłumaczenia kodu napisanego w jednym języku (języku źródłowym)
na równoważny kod w innym języku (języku wynikowym)

ZISC

Zero Instruction Set Computer
Jeden z pierwszych procesorów ZISC zawierał 36 niezależnych
komórek (uważane są za neurony lub równoległe procesory). Każda
z nich może porównać wektor wejściowy (64 bajty) z podobnym
wektorem przechowywanym w komórkach pamięci.
Jeśli wektor wejściowy odpowiada wektorowi w komórce pamięci to
komórka ta „wypala”. Sygnał wyjściowy zawiera komórki, która
miała dopasowanie, oraz znacznik mówiący, że nie wystąpiło
dopasowanie.

Schemat procesora

Rejestr (akumulator)

Pamiec (RAM)

Arytmometr

Wskazniki

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj

<adres pamięci> przepisuje zawartość pamięci o

wskazanym adresie do rejestru.

I

Zapisz

<adres pamięci> przepisuje zawartość akumulatora do

pamięci

I

Ładuj

<liczba> zapisuje liczbę do rejestru

I

Dodaj

<adres pamięci> do zawartości akumulatora dodaje

zawartość komórki o wskazanym adresie (możemy tez założyć,
że w podobny sposób potrafi policzyć różnicę, iloczyn i iloraz,
choć, w rzeczywistości, nie musi to być prawdą).
Wykonanie każdej operacji zmieniającej zawartość rejestru
powoduje ustawienie wskaźników (zero, przepełnienie, ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj

<adres pamięci> przepisuje zawartość pamięci o

wskazanym adresie do rejestru.

I

Zapisz

<adres pamięci> przepisuje zawartość akumulatora do

pamięci

I

Ładuj

<liczba> zapisuje liczbę do rejestru

I

Dodaj

<adres pamięci> do zawartości akumulatora dodaje

zawartość komórki o wskazanym adresie (możemy tez założyć,
że w podobny sposób potrafi policzyć różnicę, iloczyn i iloraz,
choć, w rzeczywistości, nie musi to być prawdą).
Wykonanie każdej operacji zmieniającej zawartość rejestru
powoduje ustawienie wskaźników (zero, przepełnienie, ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj

<adres pamięci> przepisuje zawartość pamięci o

wskazanym adresie do rejestru.

I

Zapisz

<adres pamięci> przepisuje zawartość akumulatora do

pamięci

I

Ładuj

<liczba> zapisuje liczbę do rejestru

I

Dodaj

<adres pamięci> do zawartości akumulatora dodaje

zawartość komórki o wskazanym adresie (możemy tez założyć,
że w podobny sposób potrafi policzyć różnicę, iloczyn i iloraz,
choć, w rzeczywistości, nie musi to być prawdą).
Wykonanie każdej operacji zmieniającej zawartość rejestru
powoduje ustawienie wskaźników (zero, przepełnienie, ujemne).

Podstawowe operacje

Instrukcje arytmetyczne

I

Ładuj

<adres pamięci> przepisuje zawartość pamięci o

wskazanym adresie do rejestru.

I

Zapisz

<adres pamięci> przepisuje zawartość akumulatora do

pamięci

I

Ładuj

<liczba> zapisuje liczbę do rejestru

I

Dodaj

<adres pamięci> do zawartości akumulatora dodaje

zawartość komórki o wskazanym adresie (możemy tez założyć,
że w podobny sposób potrafi policzyć różnicę, iloczyn i iloraz,
choć, w rzeczywistości, nie musi to być prawdą).
Wykonanie każdej operacji zmieniającej zawartość rejestru
powoduje ustawienie wskaźników (zero, przepełnienie, ujemne).

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje na bitach

I

Neguj

zmienia znak liczby w akumulatorze

I

And

<adres pamięci> iloczyn logiczny (bit po bicie dwu słów)

I

Or

<adres pamięci>

I

Xor

<adres pamięci> — różnica symetryczna

I

Przesun_w_lewo

I

Przesun_w_prawo

I

Przesun_cyklicznie_w_lewo

I

Przesun_cyklicznie_w_prawo

Podstawowe operacje

Instrukcje sterujące

I

Skocz

<adres pamięci> bezwarunkowe przekazanie

sterowanie do adresu

I

Skocz_jezeli_zero

<adres pamięci>

I

Skocz_jezeli_ujemne

<adres pamięci>

I

Skocz_jesli_nadmiar

<adres pamięci>

I

Skocz_do_podprogramu

<adres pamięci> bardzo podobne do

instrukcji zwykłego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pamięci

Podstawowe operacje

Instrukcje sterujące

I

Skocz

<adres pamięci> bezwarunkowe przekazanie

sterowanie do adresu

I

Skocz_jezeli_zero

<adres pamięci>

I

Skocz_jezeli_ujemne

<adres pamięci>

I

Skocz_jesli_nadmiar

<adres pamięci>

I

Skocz_do_podprogramu

<adres pamięci> bardzo podobne do

instrukcji zwykłego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pamięci

Podstawowe operacje

Instrukcje sterujące

I

Skocz

<adres pamięci> bezwarunkowe przekazanie

sterowanie do adresu

I

Skocz_jezeli_zero

<adres pamięci>

I

Skocz_jezeli_ujemne

<adres pamięci>

I

Skocz_jesli_nadmiar

<adres pamięci>

I

Skocz_do_podprogramu

<adres pamięci> bardzo podobne do

instrukcji zwykłego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pamięci

Podstawowe operacje

Instrukcje sterujące

I

Skocz

<adres pamięci> bezwarunkowe przekazanie

sterowanie do adresu

I

Skocz_jezeli_zero

<adres pamięci>

I

Skocz_jezeli_ujemne

<adres pamięci>

I

Skocz_jesli_nadmiar

<adres pamięci>

I

Skocz_do_podprogramu

<adres pamięci> bardzo podobne do

instrukcji zwykłego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pamięci

Podstawowe operacje

Instrukcje sterujące

I

Skocz

<adres pamięci> bezwarunkowe przekazanie

sterowanie do adresu

I

Skocz_jezeli_zero

<adres pamięci>

I

Skocz_jezeli_ujemne

<adres pamięci>

I

Skocz_jesli_nadmiar

<adres pamięci>

I

Skocz_do_podprogramu

<adres pamięci> bardzo podobne do

instrukcji zwykłego skoku, ale dodatkowo zapisuje aktualny
stan procesora w specjalnie do tego przeznaczonej pamięci

Asembler

Bardzo proste działanie:
A=B+C

W komórce o adresie A ma być umieszczony wynik dodawania
zawartości komórek o adresie B i C.
Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

Asembler

Bardzo proste działanie:
A=B+C
W komórce o adresie A ma być umieszczony wynik dodawania
zawartości komórek o adresie B i C.

Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

Asembler

Bardzo proste działanie:
A=B+C
W komórce o adresie A ma być umieszczony wynik dodawania
zawartości komórek o adresie B i C.
Realizacja komputerowa:
Ładuj B

Dodaj C

Zapisz A

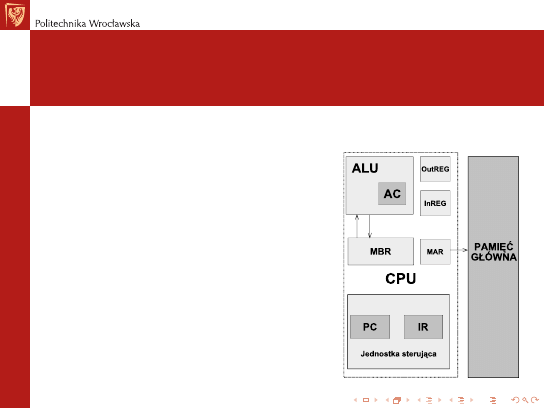
MARIE

MARIE — A Machine Architecture that is Really Intuitive and Easy

I

notacja dwójkowa, zapis w kodzie dopełnieniowym

I

przechowywanie programu, stała długość słowa

I

adresowanie słowne

I

4K pamięci głównej (12 bitów na każdy adres)

I

16-bitowe dane (16-bitowe słowa)

I

16-bitowe rozkazy (4-bitowy kod operacji + 12-bitowy adres)

I

16-bitowy akumulator (AC)

I

16-bitowy rejestr rozkazów (IR)

I

16-bitowy rejestr bufora pamięci (MBR)

I

12-bitowy licznik rozkazów (PC)

I

12-bitowy rejestr adresów pamięci (MAR)

I

8-o bitowy rejestr wejściowy (InREG)

I

8-o bitowy rejestr wyjściowy (OutREG)

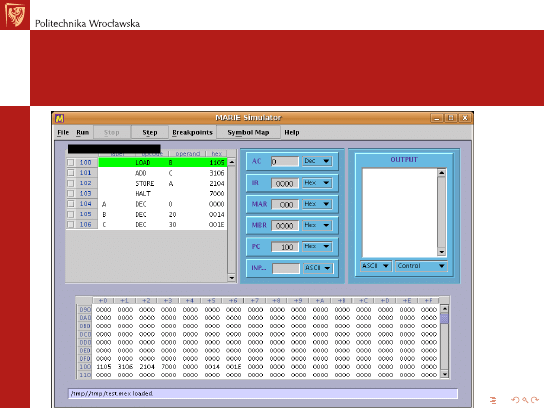
Symulator MARIE

Asembler

Bardziej skomplikowany przykład

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D

T3 = T1 ∗ T2

Z = T3/W

Asembler

Bardziej skomplikowany przykład

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D

T3 = T1 ∗ T2

Z = T3/W

Asembler

Bardziej skomplikowany przykład

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D

T3 = T1 ∗ T2

Z = T3/W

Asembler

Bardziej skomplikowany przykład

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D

T3 = T1 ∗ T2

Z = T3/W

Asembler

Bardziej skomplikowany przykład

Z =

[(

A + B)(C + D)]

W

T1 = A + B

T2 = C + D

T3 = T1 ∗ T2

Z = T3/W

Odwrotna Notacja Polska

Popatrzmy na działanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak łatwo znaleźć kalkulator który liczy „źle”?

Odwrotna Notacja Polska

Popatrzmy na działanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak łatwo znaleźć kalkulator który liczy „źle”?

Odwrotna Notacja Polska

Popatrzmy na działanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?

Czemu tak łatwo znaleźć kalkulator który liczy „źle”?

Odwrotna Notacja Polska

Popatrzmy na działanie:

3 + 7 × 5

Ile wynosi wynik?

50 czy 38?

A który jest poprawny?
Czemu tak łatwo znaleźć kalkulator który liczy „źle”?

„Ważność” działań arytmetycznych

1.

potęgowanie

2.

mnożenie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mogą ją zmieniać!

„Ważność” działań arytmetycznych

1.

potęgowanie

2.

mnożenie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mogą ją zmieniać!

„Ważność” działań arytmetycznych

1.

potęgowanie

2.

mnożenie i dzielenie

3.

dodawanie i odejmowanie

Nawiasy mogą ją zmieniać!

Czy jest możliwy zapis jednoznaczny?

Polski logik, Łukasiewicz, wprowadził notację „przedrostkową”.
Zamiast

z = x + y zaproponował zapis:

+

xy

Zwracam uwagę że jest on bardzo podobny do zapisu funkcji dwu
zmiennych:

z = f(x, y)

Funkcja suma jest też dwuargumentowa:

z = +(x, y)

Czy jest możliwy zapis jednoznaczny?

Polski logik, Łukasiewicz, wprowadził notację „przedrostkową”.
Zamiast

z = x + y zaproponował zapis:

+

xy

Zwracam uwagę że jest on bardzo podobny do zapisu funkcji dwu
zmiennych:

z = f(x, y)

Funkcja suma jest też dwuargumentowa:

z = +(x, y)

Zapis polski

Działanie

3 + 7 × 5 oznaczające 3 + (7 × 5) zapisujemy:

+ ×

7 5

| {z }

3

|

{z

}

odwrotny zapis polski

Utarło się używanie innego zapisu: najpierw podaje się argumenty
działania, później samo działanie:

xy+

Stąd nazwa: „Odwrotna notacja polska”.
Nasze działanie zapisujemy tak:

7 5 × 3+

a to bardziej skomplikowane tak:

A B + C D + ×W /

Odwrotna Notacja Polska — stos

Praktyczna realizacja działania

A B + C D + ×W /

wymaga stosu. I dodatkowych operacji w języku wewnętrznym:

I

Zapisz_na_stos

przepisuje zawartość akumulatora na stos.

I

Pobierz_ze_stosu

pobiera ze stosu wartość i przepisuje ją do

akumulatora

Stos

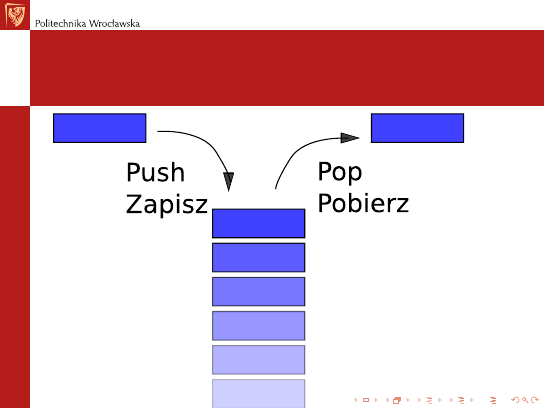
Stos

Prosty kalkulator

http://www.calculator.org

Praktyczna realizacja działania

A B + C D + ×W /

A = 1, B = 2, C = 3, D = 4, W = 5

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

Arytmetyka komputerów

I

Zapis liczb — dwójkowy.

I

Każda z liczb zapisywana jest za pomocą cyfr 0 i 1.

I

Układ jest pozycyjny — waga cyfry zależy od miejsca, w którym
została ustawiona.

I

Najmniej znaczące miejsca są po stronie prawej. . .

I

1010 to

1 × 2

3

+

0 × 2

2

+

1 × 2

1

+

0 × 2

0

czyli

8 + 0 + 2 + 0 = 10

I

NB liczby parzyste mają zero na końcu, nieparzyste — 1.

I

Arytmetyka dwójkowa — bardzo prosta.

I

0 + 0 = 0

I

1 + 0 = 0 + 1 = 1

I

1 + 1 = 10

I

1 × 1 = 1

I

1 × 0 = 0 × 1 = 0

I

0 × 0 = 0

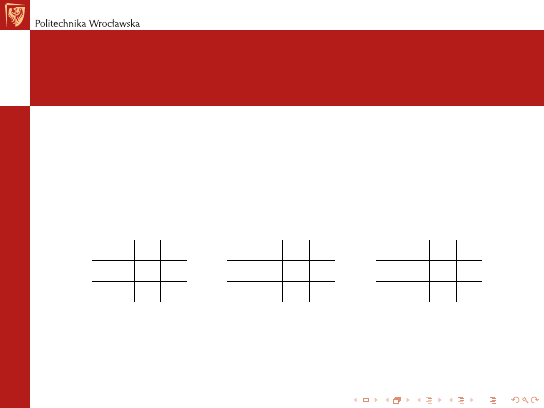
Operacje logiczne

(Podstawowe) operacje logiczne to suma logiczna (OR), iloczyn
logiczny (AND), negacja (NOT), różnica symetryczna (XOR)

OR

0

1

0

0

1

1

1

1

AND

0

1

0

0

0

1

0

1

XOR

0

1

0

0

1

1

1

0

Arytmetyka komputera

Arytmetyka „klasyczna”

Jesteśmy przyzwyczajeni do następujących „rzeczy”:

1.

Jeżeli

x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powyższe zasady nie obowiązują!

Arytmetyka komputera

Arytmetyka „klasyczna”

Jesteśmy przyzwyczajeni do następujących „rzeczy”:

1.

Jeżeli

x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powyższe zasady nie obowiązują!

Arytmetyka komputera

Arytmetyka „klasyczna”

Jesteśmy przyzwyczajeni do następujących „rzeczy”:

1.

Jeżeli

x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powyższe zasady nie obowiązują!

Arytmetyka komputera

Arytmetyka „klasyczna”

Jesteśmy przyzwyczajeni do następujących „rzeczy”:

1.

Jeżeli

x 6= 0 to ∀a a + x 6= a

2.

a + b + · · · + z = z + y + · · · + b + a

3.

∀

a, b ∈ < a < b ∃c : a < c < b

W arytmetyce komputerowej powyższe zasady nie obowiązują!

Liczby „zmiennoprzecinkowe”

1.

Arytmetyka

1.1

Liczby naturalne

1.2

Liczby całkowite

1.3

Liczby wymierne

1.4

Liczby rzeczywiste

2.

Komptery

2.1

Liczby całkowite („integer”)

2.2

Liczby „stałoprzecinkowe”

2.3

Liczby „zmiennoprzecinkowe”

Liczby całkowite I

I

Sytuacja dosyć klarowna.

I

Na

n bitach możemy zapisać liczby całkowite dodatnie z

zakresu od zera do

2

n

−

1

I

Jest pewien problem z liczbami ujemnymi: trzeba zarezerwować
miejsce na znak

I

Trzeba to tak zrobić, żeby podstawowe operacje (dodawanie,
odejmowanie i mnożenie,. . . ) były wykonywane tak samo gdy
argumenty są dodatnie jak i wtedy gdy są ujemne.

I

Układ „uzupełnieniowy” to załatwił.

Liczby całkowite II

I

Czasami korzysta się z kodu BCD (Binary Coded Decimal —
(cyfry) dziesiętne kodowane binarnie: liczba zapisywana jest w
układzie dziesiętnym (za pomocą cyfr dziesiętnych), ale
poszczególne cyfry kodowane są binarnie
321

(

10)

zapisywane jest jako

0011 0010 0001

2

Liczby „stałoprzecinkowe”

1.

Liczby w których na zapamiętanie części całkowitej przeznacza
się kilka(naście/dziesiąt) bitów

2.

Na zapamiętanie części ułamkowej również używa się
kilku(nastu?) bitów:

1

0

1

0

,

1

0

1

0

co odczytujemy jako:
1∗2

3

+

0∗2

2

+

1∗2

1

+

0∗2

0

+

1∗2

−

1

+

0∗2

−

2

+

1∗2

−

3

+

0∗2

−

4

lub

8 + 2 +

1

2

+

1

8

czyli 10,625

3.

Używany bardzo rzadko (finanse??)

4.

Z matematycznego punktu widzenia są to liczby wymierne

5.

Jak w tej postaci zapisać liczbę 1,1

Liczby „zmiennoprzecinkowe” I

1.

Są to liczby zapisywane (kodowane) w sposób podobny do
zananego nam:

c = 299792458 ∼ 3 ∗ 10

8

m/s

2.

Czyli w postaci mantysa (2,99792458) plus wykładnik 8, zatem
2,99792458*10

8

albo inaczej 2,99792458 e8

3.

W przypadku komputerów podstawa kodowania (tak mantysy
jak i wykładnika) to 2!

4.

Dodatkowo liczby zapisywane są zawsze w postaci
„znormalizowanej” czyli takiej, że cyfra przed przecinkiem
(kropką) dziesiętnym jest zawsze z zakresu między 1 a 9. (a w
układzie dwójkowym zawsze jest równa 1!)

5.

Na zapamiętanie mantysy i wykładnika przeznaczana jest
zawsze skończona liczba bitów.

Liczby „zmiennoprzecinkowe” II

6.

Z matematycznego punktu widzenia są to liczby wymierne.

7.

Sposób zapisu liczb zmiennoprzecinkowych reguluje standard
IEE-754.

Parę problemów

1.

Zawsze(?) ograniczona liczba bitów przeznaczona na
zapamiętanie liczby (ale znane są specjalne programy, które
starają się te ograniczenie przezwyciężać).

2.

Wynik działań arytmetycznych często prowadzi do powstania
nadmiaru (czyli przekroczenia maksymalnej dopuszczalnej
wartości liczb).

3.

Większość liczb który (z przyzwyczajenia) traktujemy jako
dokładne nie ma dokładnej reprezentacji dwójkowej (0,5 jest
OK ale 0,1 już nie.